多约束条件下六自由度机械臂最优时间轨迹规划

马腾宇，胡孝楠，郭新华

(武汉理工大学 机电工程学院，湖北 武汉 430070)

时间最优轨迹规划是提高空间机械臂效率的关键[1]，空间机械臂的轨迹规划和控制算法，为机械臂的平稳运行和工作效率的提高提供保障[2]。在空间机械臂的工业应用中，时间最优性对于生产效率的最大化是至关重要的[3]，时间作为轨迹规划的重要指标，可以直接反映空间机械臂的效率[4]。此外，机械臂在运动过程中还应满足各关节的多重动力学约束。因此，在满足运动约束的条件下，减少机械臂的工作时间是解决该问题的关键。

针对这一问题，Papadopoulos等[5]提出了一种利用多项式函数来跟踪关节轨迹的方法，使机械臂的运动轨迹更加平滑。Saravanan等[6]利用三次样条函数来描述关节轨迹，并用差分进化算法对问题进行了优化。Wei等[7]采用遗传算法求解最优轨迹，然而，遗传算法的迭代过程非常复杂，需要在找到最优解后进行编码和解码处理。Chen等[8]利用和声搜索算法寻找最优解，但在重要参数值和声记忆库取值概率以及微调概率的选择上需要进行改进。粒子群算法也常用于机械臂的轨迹优化问题。Jin等[9]利用标准粒子群算法求解冗余度机械臂逆运动学问题。Akbarimajd[10]采用自适应粒子群算法对三自由度机械臂的运动时间进行优化，并通过在机械系统动力学自动分析的仿真中验证了算法的有效性。Kim等[11]提出了一种利用标准化步长来初始化粒子群的方法。Wang等[12]使用粒子群算法跟踪自由漂浮的空间机器人的轨迹。然而，标准粒子群算法存在早熟收敛的缺点，容易收敛到局部极值。

笔者提出了一种时间最优的空间机械臂轨迹规划方法。首先，利用D-H参数法建立六自由度机械臂运动学模型，其次，根据逆运动学的方法将笛卡尔坐标系中的轨迹点转化为关节空间中的轨迹点，利用3-5-3样条函数表示关节角轨迹，然后根据运动约束生成各关节的适应度函数，最后，采用改进的粒子群算法对每个关节的运动时间进行优化，从而得到最优解。

1 六自由度机械臂建模

为了使优化过程更加直观，以一个具有6个旋转自由度的刚性机械臂为研究对象。前3个关节确定机械臂末端执行器的位置，后三个关节确定末端姿态。采用D-H参数法建立运动学模型，D-H参数法包含4个参数：θ为关节变量，d为连杆长度，α为关节扭转角，a为关节偏移量。整个机械臂系统的关节坐标系如图1所示。

机械臂的D-H参数如表1所示。六自由度机械臂各关节的转动惯量如表2所示。

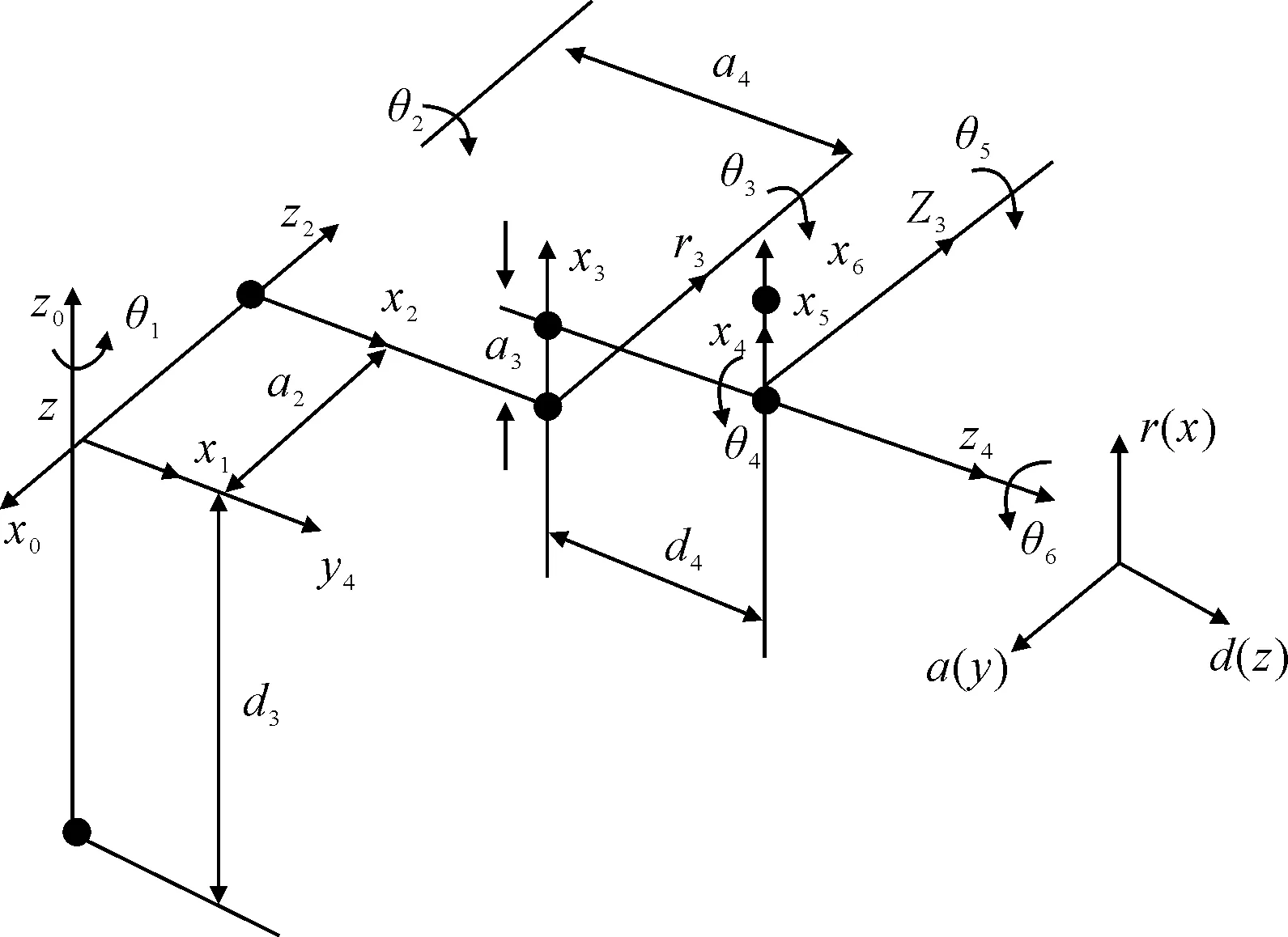
图1 六自由度机械臂关节坐标系

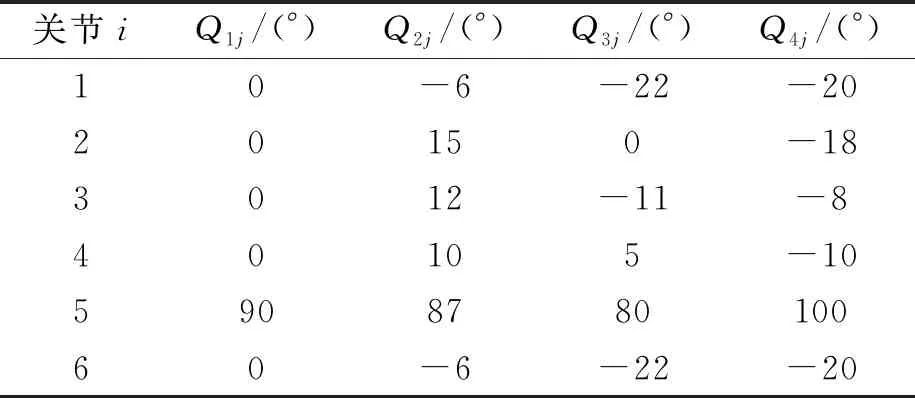
表1 D-H 参数表

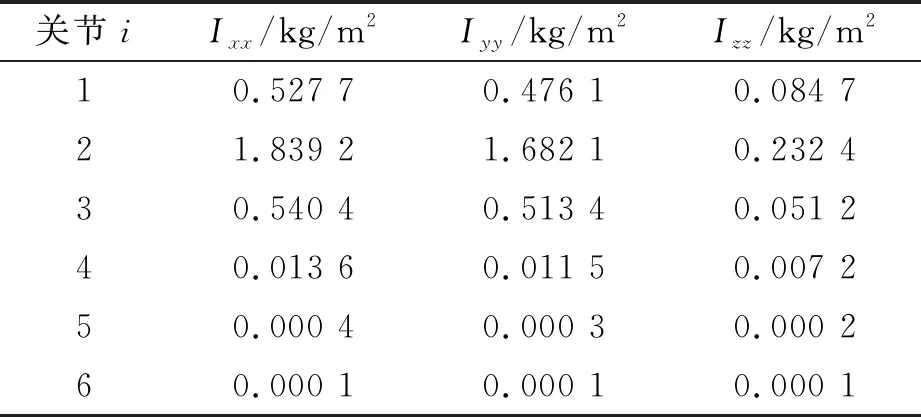
表2 各关节转动惯量

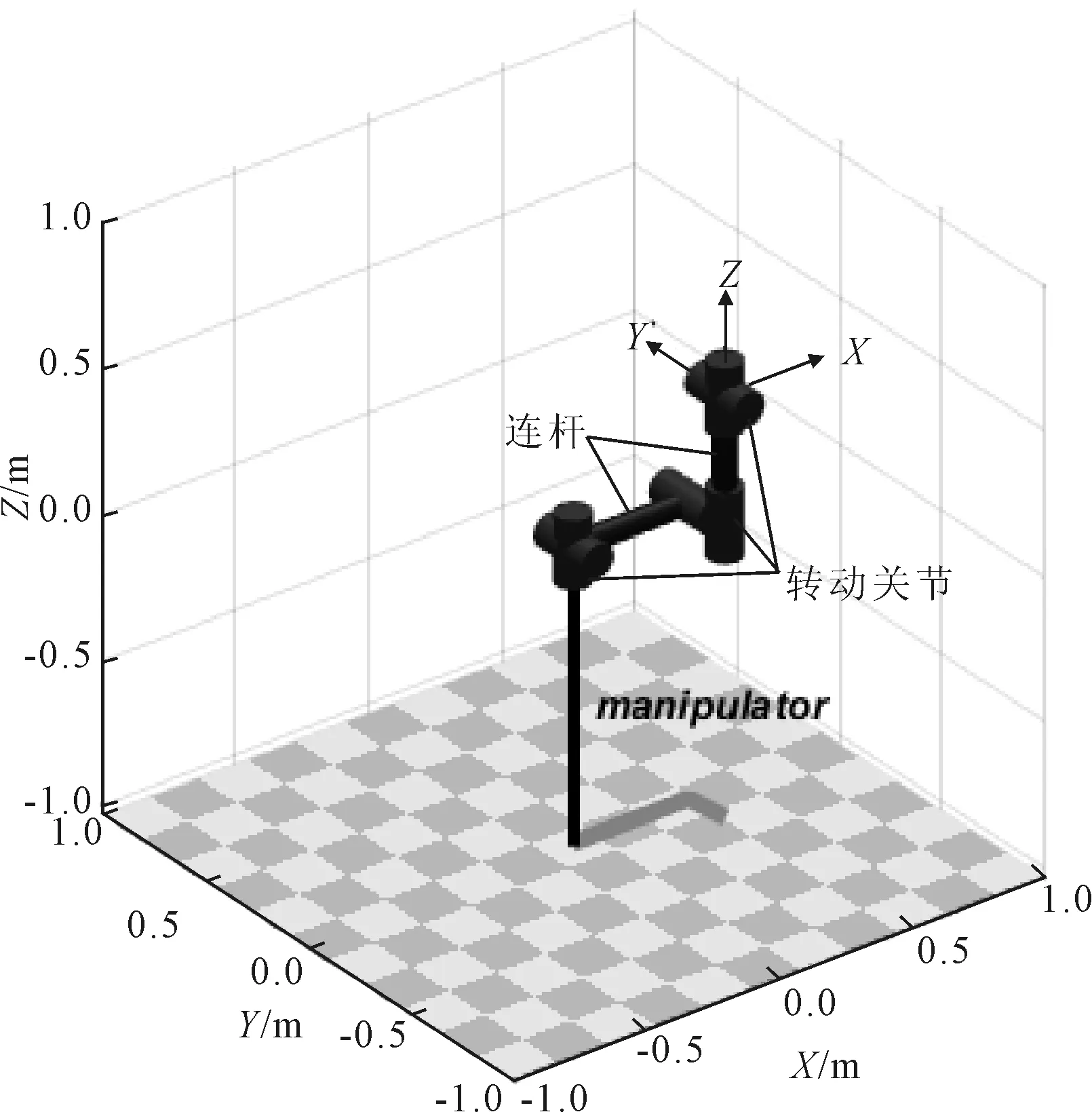
图2 六自由度机械臂简易模型

基于表1中的特征参数，建立机械臂简化模型，如图2所示，每个关节的初始角度设置为0度。机械臂的结构图如图3所示。文中默认机械臂处于理想状态，对末端执行器和传感器的失效以及外界干扰具有免疫性。

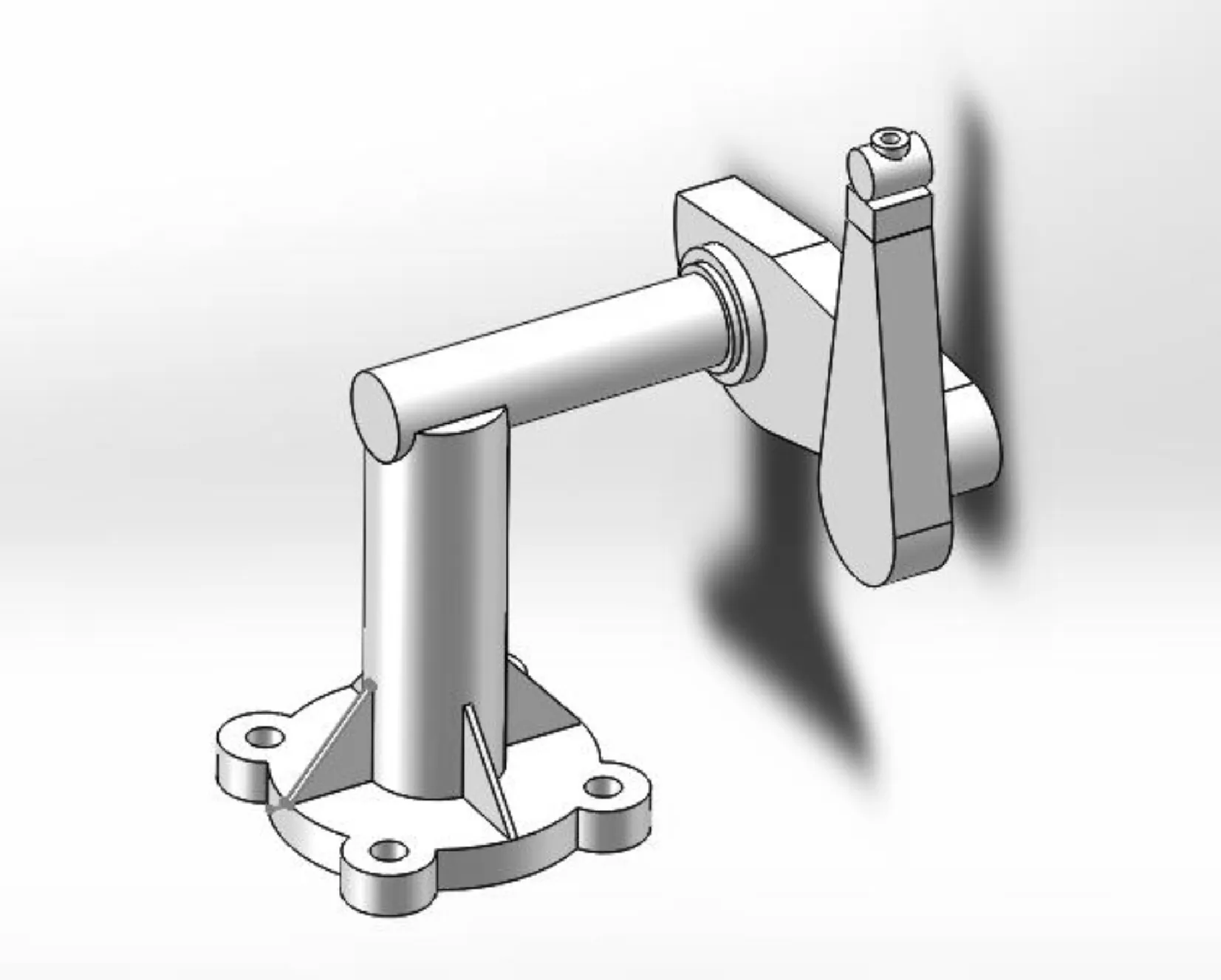
图3 六自由度机械臂结构图

2 轨迹规划问题的描述

一般情况下，根据预设的任务要求，可以得到关节空间中的一系列路径点：θ={θsr|s=1,2,…，m;r=1,2,…，n}，其中θsr为关节s第r个路径点的位置，m为关节总数，n为路径点的总数。在路径点的生成过程中，机械臂的奇点尤为重要，六自由度机械臂在运动过程中遇到腕部奇点、肩部奇点和肘部奇点时，都会发生卡滞现象，因此在生成路径时要避免这些奇点的出现。

在得到每个关节的路径点后，需要对关节角度进行参数化处理，笔者采用3-5-3样条函数对关节角进行描述。为了简化计算过程，对关节的运动时间进行了归一化处理，并引入一个表示无量纲时间的参数t[13]：

(1)

式中：j为时间维度，j=1，2，3；τ为轨迹的实际时间，τ∈[τj-1，τj]，τj-1和τj分别为第j段轨迹的开始时间和结束时间，每段轨迹的方程如下[13]：

(2)

其中θ1(t),θ2(t),θ3(t)为三段多项式轨迹函数。机械臂在起始点的关节角、速度和加速度分别表示为θ0,v0,a0；终点的值分别表示为θf,vf,af。方程中的系数可由轨迹的连续性和中间点的位置、速度和加速度的连续性得到：

(3)

a13=Δθ1-a11-a12

(4)

(5)

(6)

根据式(3)～式(6)可以得到b1～b3和a23～a25的值：

(7)

(8)

在得到所有未知参数后，可以得到每个关节的运动轨迹。

在机械臂的实际工作过程中，从起点到终点的运动时间应尽可能短。在保证最优时间的同时，还要考虑各关节的运动约束，使运动轨迹更加平滑。综合考虑最优时间和多重约束的影响，适应度函数的定义如下：

(9)

(10)

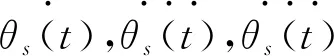
经过上述步骤，将问题转化为多约束条件下求解适应度函数的最小值问题。当机械臂不能满足约束条件时，可将适应度函数值设为最大值fitnessmax。

3 轨迹优化算法

为了克服标准粒子群算法容易收敛到局部最优解的问题，对标准算法进行了改进。改进算法的特点如下：①利用混沌序列增加粒子群的多样性，增加多样性参数来检测粒子的离散状态，使得粒子群在混沌和稳定性之间达到平衡。②如果每一个粒子的当前最优解经过5次迭代后都没有改变，则增加粒子的惯性权重，使其能够及时逃离局部极值。③利用当前适应度函数和迭代次数的值对惯性权重ω进行自适应调整，增加全局搜索和局部搜索的协调性。改进算法流程如图4所示。

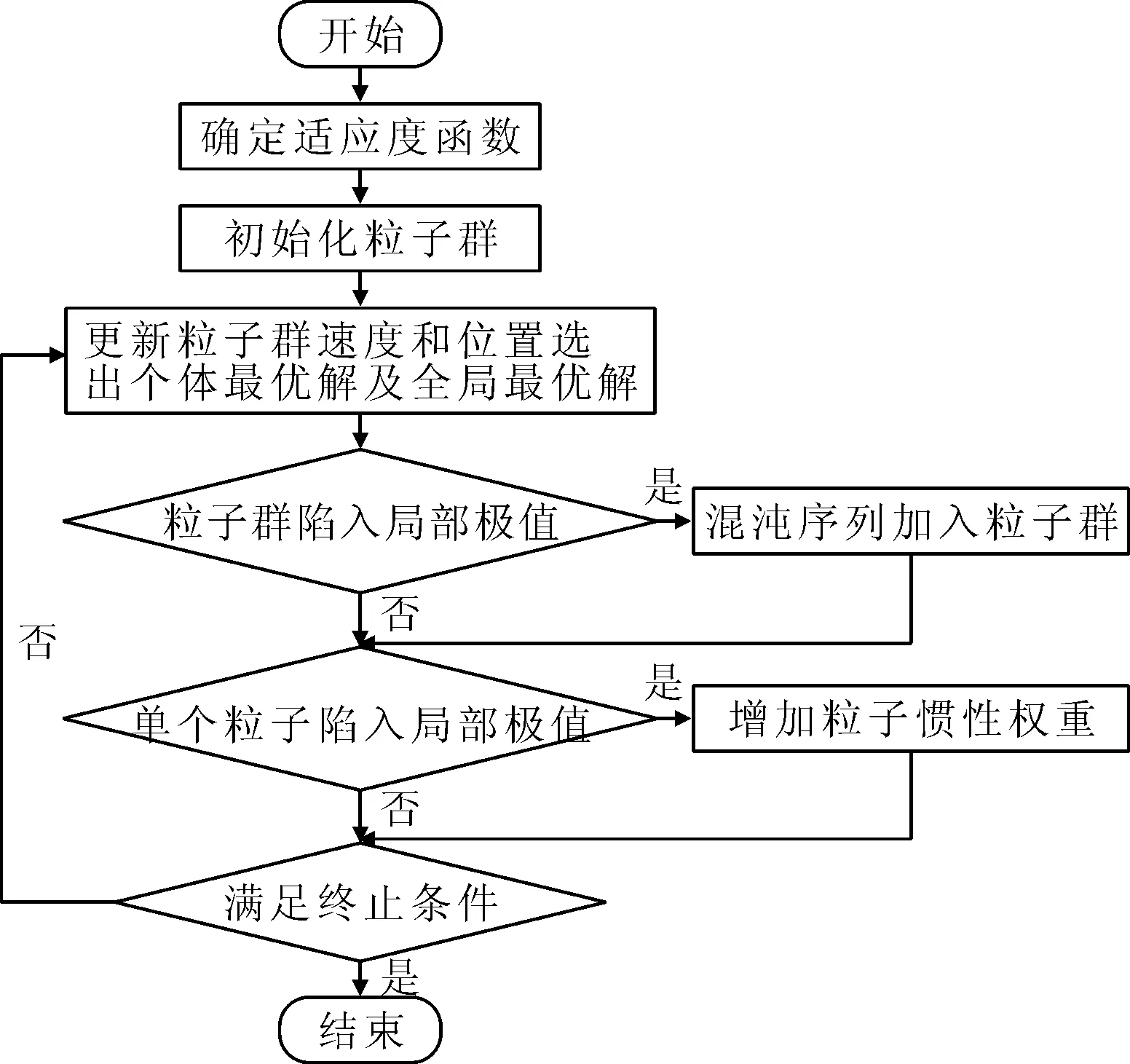
图4 算法流程图

改进算法的具体步骤如下：

步骤1设置参数T,ω,c1,c2,D的值，T为迭代的最大代数，ω为惯性权重，c1,c2为学习因子，D为维度。

步骤2利用混沌序列对粒子位置和速度进行初始化。粒子的初始值由帐篷映射生成，然后映射到解空间，通过式(9)计算适应度函数，选择最佳的一部分粒子作为初始粒子群。

步骤3选择适应度函数最小的粒子作为全局最优粒子。

步骤4粒子的值由式(11)和式(12)更新[14]：

νij(k+1)=ωνij(k)+c1r1(pij(k)-xij(k))+

c2r2(gj(k)-xij(k))

(11)

xij(k+1)=xij(k)+νij(k+1)

(12)

式中：i为粒子序数；k为当前迭代步长；νij为速度值；xij为位置值；pij为个体最优极值；gj为全局最优极值；r1和r2为0到1之间的随机数。惯性权重ω通过式(13)进行更新：

(13)

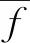
学习因子c1和c2分别体现了自我探索和群体学习能力。在优化算法的初始阶段，粒子应该具有较强的自我探索能力和较弱的群体学习能力，以增强粒子的整体搜索能力；在后期的搜索中，粒子应具有较弱的自我探索能力和较强的群体学习能力，以保证粒子趋向全局极值。学习因子根据式(14)进行更新：

(14)

式中：c1max、c2max为学习因子的最大值；c1min、c2min为学习因子的最小值。

如果迭代后粒子的位置和速度超过预设值，则以区间的上下限作为粒子的位置和速度值。

步骤5适应度函数的方差按式(15)计算：

(15)

式中：N为粒子总数。

M为种群多样性参数，用来衡量粒子群的分散程度，M是一个常数，根据不同的情况分配。如果σ2>M，说明粒子群的多样性较高，则跳到步骤7；如果σ2

步骤6全局最优粒子g=(g1,g2,…,gj)按式(16)映射到解空间[15]：

(16)

其中aj和bj是维度j的边界值。以zj 0为初始状态，利用帐篷映射生成新的混沌粒子z′= [z′1,z′2,…,z′h]，将新的混沌序列映射到解空间，得到新粒子的位置g′=[g′1,g′2,…,g′h]。

计算新的h个粒子的适应度函数值，选择最佳粒子g′best，用最小适应度函数值的粒子替换原粒子群。

步骤7判断每个粒子的个体最优极值，如果极值在5次迭代中没有变化，则根据式(17)重新计算粒子的惯性系数：

(17)

粒子在迭代开始时不容易收敛到局部极值，随着迭代次数来改变ω的值，使其在迭代后期增加惯性权重，及时逃离局部极值。

如果算法达到迭代次数的最大值，则迭代结束，否则跳到步骤4。

4 仿真结果分析

以六自由度机械臂为研究模型，为了评价改进粒子群优化算法的有效性，将其与标准粒子群优化算法[16]和遗传算法[17]进行对比，每种算法迭代100次，实验参数设置如下：

机械臂关节速度约束为[-40 40](deg/s)，加速度约束为[-60 60](deg/s2)，标准粒子群算法的参数设置为N=20,ωmin=0.4,ωmax=0.9,D=3,T=100。

改进粒子群算法的参数设置为N=20,ωmin=0.4,ωmax=0.9,c1=1.49,c2=1.49,D=3,T=100。遗传算法采用二进制编码，每一代种群通过轮盘赌选择法进行更新，交叉概率Pc和变异概率Pm分别设置为0.6和0.001。

关节空间的路径点如表3所示。

表3 关节路径点

在多约束条件下，仿真以最短时间为目标进行模拟。利用改进的粒子群算法求解，得到6个关节的运动时间，并利用每个维度的最大值来形成最优时间：fitness=[1.96 2.92 2.45]。以第一关节的运动时间为例，将改进的粒子群算法与经典的粒子群算法和遗传算法进行了比较，结果如表4所示。

从表4可知，粒子群算法的时间比遗传算法缩短了很多，主要是因为遗传算法的编码解码过

表4 仿真结果

程比较复杂，导致寻找最优解的速度降低。这3种算法的优化过程如图5所示。结果表明，改进后的粒子群算法比标准算法收敛速度快，最优解也优于标准粒子群算法和遗传算法，经过30次迭代后，标准粒子群算法陷入局部极值，最终的最优解远低于改进的粒子群算法。

图5 算法迭代过程

图6 6个关节的角度、速度和加速度比较

6个关节的角度、速度和加速度的曲线如图6所示，横坐标为机械臂的运动时间，纵坐标为关节的角度、速度和加速度的数值。从图6可知，关节角的运动曲线是非常平滑的，最大速度不超过35 deg/s，最大加速度不超过50 deg/s2，因此机械臂的运动在预设的约束值之内。初始速度和加速度为0，保证了关节的初始扭矩为0，从而减小了机械臂的损耗。

5 结论

笔者提出了一种多约束条件下六自由度机械臂最优时间轨迹规划方法。针对标准粒子群算法容易早熟收敛以及求解不精确的缺点，提出了一种改进的粒子群算法。通过建模和推导，将轨迹规划问题转化为用改进粒子群算法求解全局最优解的问题。将该算法与标准粒子群算法和遗传算法进行了比较，仿真结果表明，所提出的优化算法更容易、更快地找到最优解，大大降低了早熟收敛的概率，加快了收敛速度，改进的粒子群算法是一种有效的时间最优轨迹规划算法。