视觉挠度测量系统中的相机抖动误差消除研究

周 晓，王进举，李新成

(武汉理工大学 机电工程学院，湖北 武汉 430070)

近年来，随着机器视觉的发展，对视觉挠度测量系统的研究越来越多，有很多学者将其应用到不同的场景中，如桥梁、起重机、路面测量等[1-4]。现有的视觉挠度测量系统理论上能够达到亚像素级精度，但是在测量过程中，由于周围环境的影响如气流、相机安装不稳固、地面震动等，会引起相机产生抖动。相机抖动会造成图像中的待测点产生位置变化，并且随着测量距离的增加，即使微小的抖动也会引起极大的测量误差。因此有必要对相机抖动进行研究，减小影响，使之能够达到稳定的亚像素级精度。

目前，国内学者对于相机抖动误差消除研究较少，国外有学者通过设计更加稳固的相机安装方式来减小抖动，但是该方法效果不好，除非相机能达到绝对的稳定[5-6]，也有学者通过使用一个固定的参考点，将待测点的挠度减去参考点的挠度，消除由于相机平移运动引起的误差，但是对于相机旋转引起的误差不能有效消除[7-10]。

笔者针对视觉挠度测量系统中相机抖动引起的误差，提出了利用两个固定参考点进行相机抖动误差消除的模型，解决了视觉挠度测量系统中周围环境对于测量精度影响过大的问题。试验证明，结合亚像素定位技术能够实现稳定的亚像素精度测量。

1 相机抖动误差产生原理

1.1 相机抖动成像运动分析

在视觉挠度系统测量过程中，由于周围环境的影响如地面的震动、气流的流动、相机安装不能达到绝对稳定等，会导致相机发生无规则的抖动。相机没有抖动时采集的图像通过算法获取待测点的位置，将会是真实位置；当相机发生抖动时，图像中待测点位置和物理位置会发生偏差，导致视觉挠度测量产生误差。

在视觉挠度测量试验中，通过静态试验，即保证待测点静止不动，对数据进行分析，发现即使相机使用专用的三脚架固定，图像中的待测点坐标也会发生很大的漂移和波动。因此，想要通过固定相机的方式防止相机发生抖动比较困难，尤其是在远距离和室外工况中。基于此，笔者提出通过在待测挠度位置附近选择两个固定参考点进行相机抖动误差消除。

假设存在一个挠度待测点，而两个固定参考点分布在待测点附近的位置，待测点和参考点在图像中的运动有4种情况：

(1)相机无抖动，待测点位置未发生变化；

(2)相机无抖动，待测点位置发生变化；

(3)相机有抖动，待测点位置未发生变化；

(4)相机有抖动，待测点位置发生变化。

在视觉挠度测量中，大多数是第4种情况，即相机发生抖动，固定参考点由于相机抖动在图像中的位置发生变化，而待测点在图像中的位置变化原因是：待测点自身位置的移动和相机抖动。

1.2 相机抖动误差分解

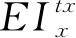
(1)

图1 相机抖动的运动分解

如果仅采用一个固定的参考点，参考量太少，仅能消除相机x和y方向的平移误差。通过采用两个参考点，可以建立相机的平移和旋转误差模型，求解出式(1)。

2 相机抖动误差校正

2.1 相机绕z轴旋转误差校正

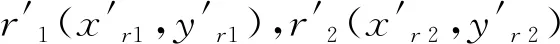
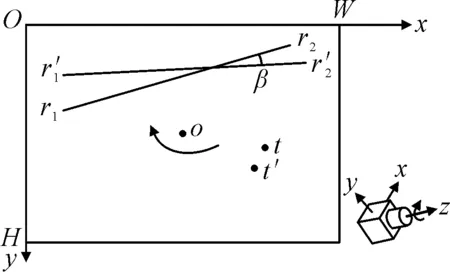
图2 相机绕z轴旋转前后的成像变化图

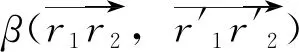
(2)

(3)

最后，根据旋转前后的待测点坐标和式(2)求出的旋转角度β，进而求得相机绕z轴旋转引起的待测点水平和竖直方向的误差：

(4)

图3 相机绕z轴旋转引起的误差图

从图3可知，当旋转角度不变时，误差会随着待测点和图像中心的距离增大而增加；当待测点和图像中心的距离不变时，误差随着相机旋转角度的增大而增加。并且，当待测点在图像中心时，相机绕z轴旋转引起的误差最小为0；当旋转角度β=±0.005°，并且待测点坐标t(xt,yt)处于图像左上、右上、左下、右下4个顶点时，误差值达到最大。表1列出了相机绕z轴旋转引起的几个关键误差值，可以看出即使很小的旋转角度β=±0.005°，x方向的误差可以达到0.131 pixel，y方向的误差可以达到0.178 pixel，而亚像素定位算法的精度为0.05 pixel，极大程度地影响了视觉测量精度，因此非常有必要采用两个固定的参考点进行相机绕z轴旋转误差的消除。另外根据图3可知，可以使待测点的成像位置尽量靠近图像中心来减小相机绕z轴旋转引起的误差。

表1 相机绕z轴旋转的关键误差值

2.2 相机绕x轴和y轴旋转的误差校正

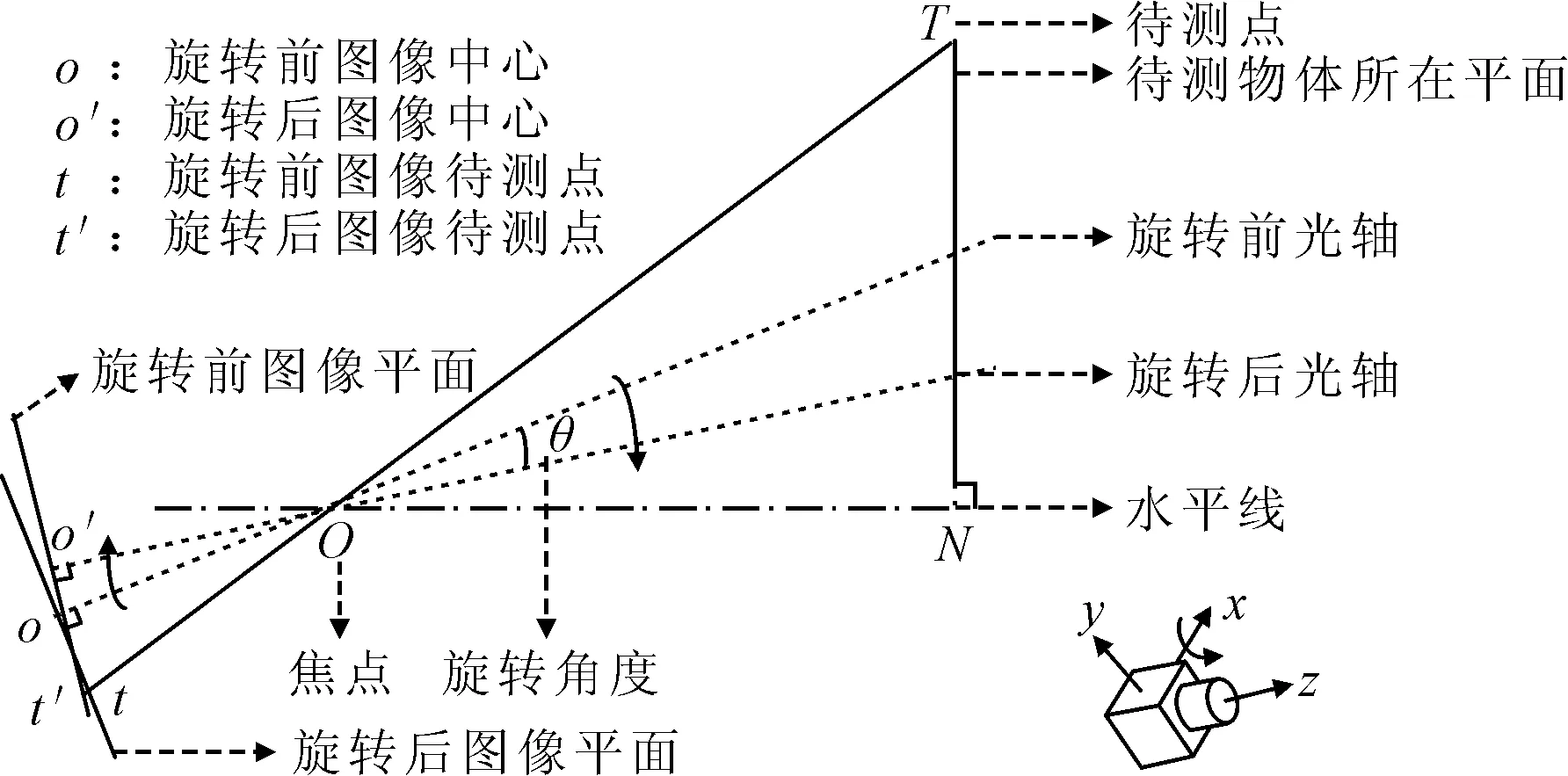
图4 相机绕x轴旋转前后待测点和参考点位置变化

根据几何关系和成像原理可得如下关系：

(5)

式中：Po′t′和Pot分别为o′t′和ot在物理空间中相对应的距离；f为镜头焦距。

相机绕x轴旋转引起的y方向上的误差可推导如下：

(6)

同理可以推导出相机绕y轴旋转引起的x方向上的误差公式为：

(7)

从式(6)和式(7)可以看出，相机绕x轴和y轴旋转引起的误差和镜头焦距、尺度转换因子、待测点的图像坐标和相应的旋转角度有关。

假设相机焦距f=50 mm，H=3 000 pixel，W=4 096 pixel，根据式(6)绘制相机绕x轴旋转的误差绝对值图形，如图5所示。其中，图5(a)为y方向尺度转换因子kty=1 mm/pixel时，误差绝对值随旋转角度和待测点y坐标的变化图。由图5(a)可知，旋转角度θ不变时，待测点y方向距离图像中心越远，误差越大；待测点y方向距离图像中心不变时，旋转角度θ越大，误差越大。图5(b)为θ=0.005°时，误差绝对值随尺度转换因子和待测点y坐标的变化图。由图5(b)可知，尺度转换因子kty不变时，待测点y方向距离图像中心越远，误差越大；待测点y方向距离图像中心不变时，kty越大，误差越大。

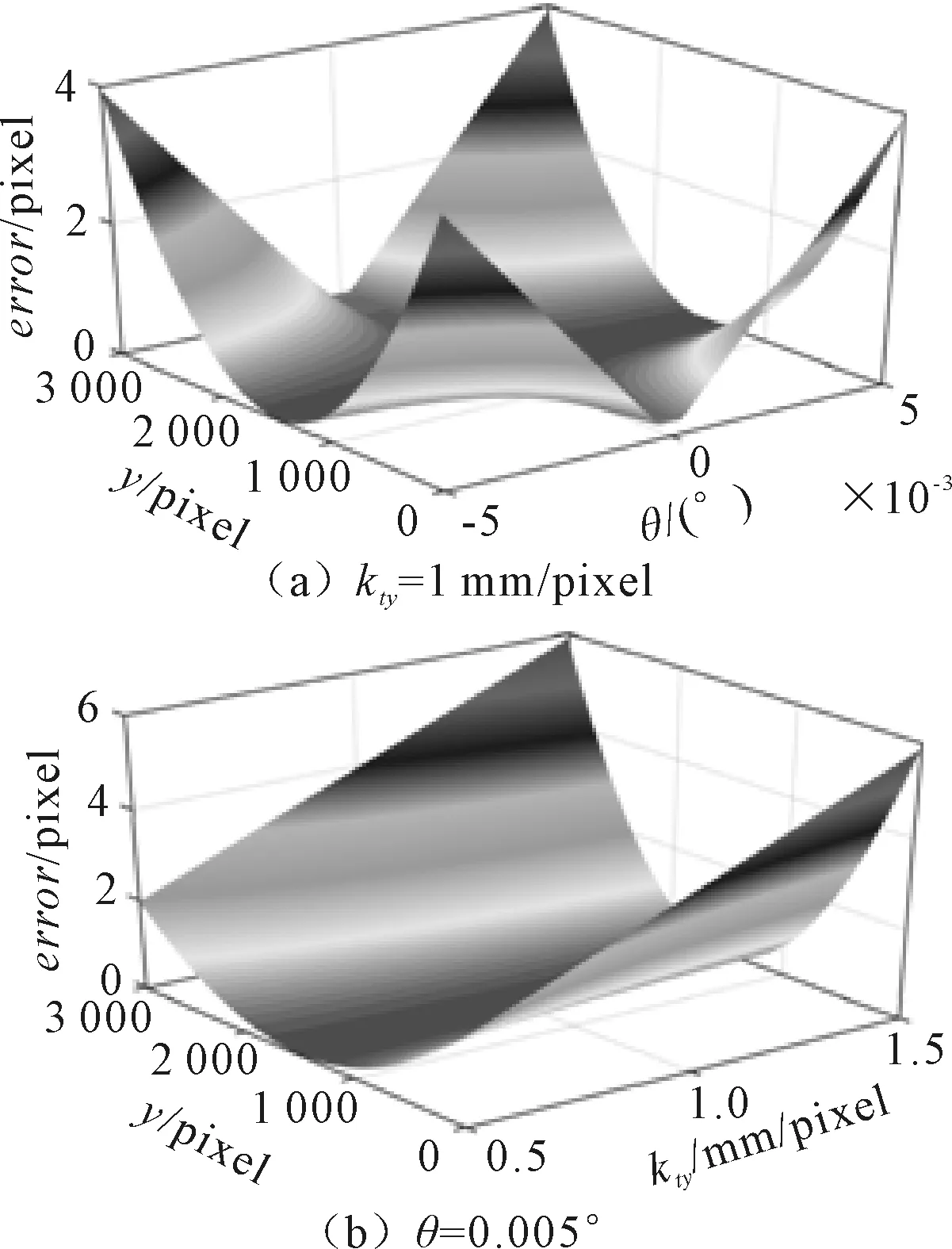
图5 相机绕x轴旋转误差绝对值变化图

同理根据式(7)绘制相机绕y轴旋转的误差绝对值图像，如图6所示。从图6可以得到和相机绕x轴旋转类似的误差结论：待测点x方向距离图像中心越远、旋转角度越大以及尺度转换因子ktx越大，误差越大。

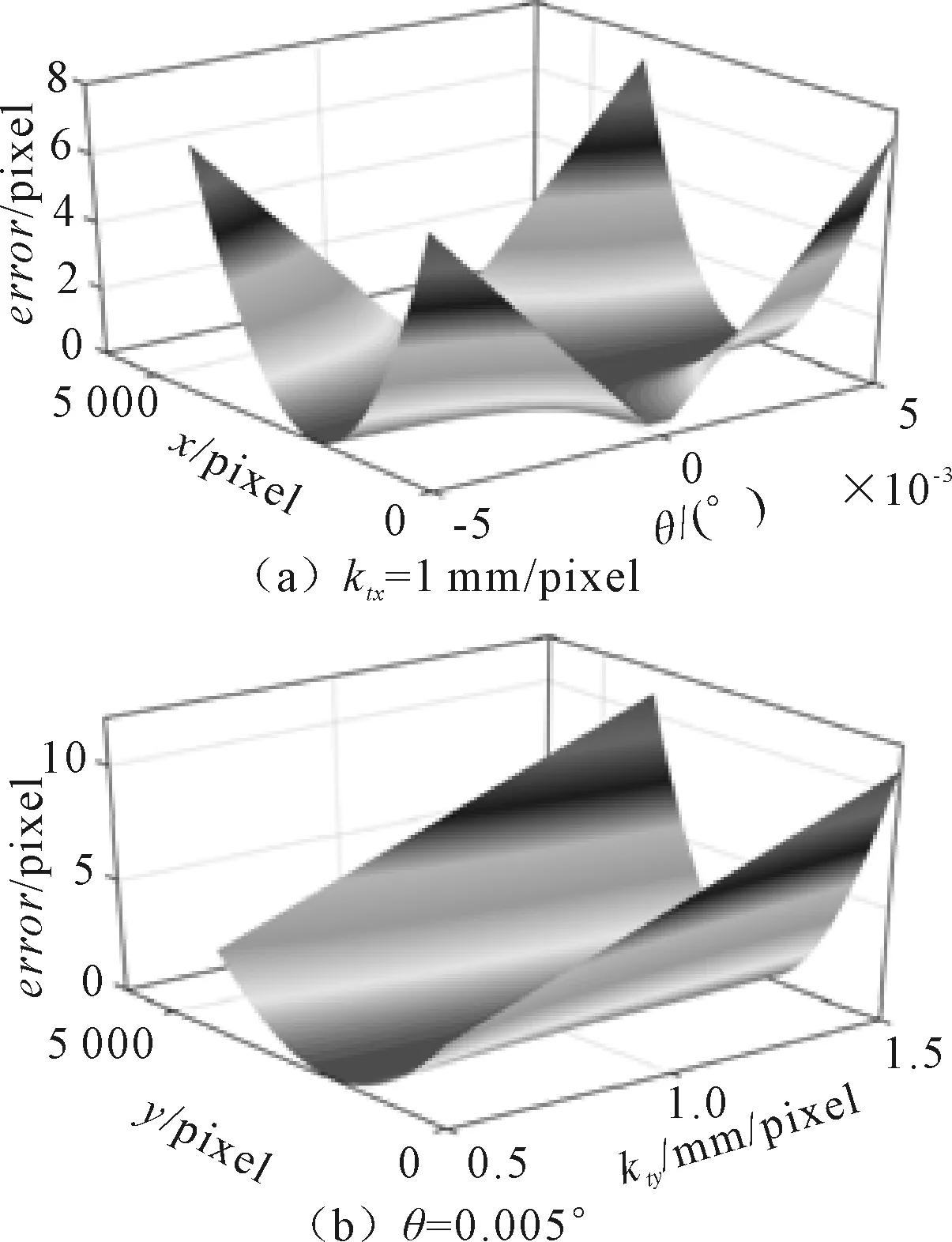
图6 相机绕y轴旋转误差绝对值变化图

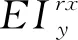
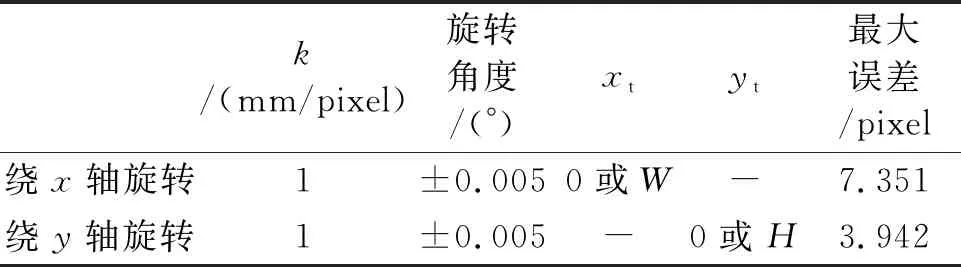
表2 相机绕x轴和y轴旋转的关键误差值

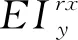
(8)

(9)

式中，σ为图像平面内r1r2与水平线的夹角。

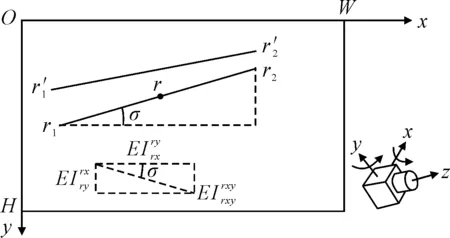
图7 相机绕x轴和y轴旋转的误差分解

根据图3得到的结论可知，误差随着待测点和图像中心距离的增加而增大，为了简化运算，假设为线性增长，则待测点处的误差为：

(10)

因此，可以根据起始帧图像待测点的坐标和两个参考点的坐标求解出相机绕x轴和y轴旋转引起的误差。

2.3 相机平移误差校正

对于相机平移运动造成的误差，可利用两个参考点连线的中点坐标变化求解，公式如下：

(11)

综上所述，可以使用两个固定参考点将相机抖动造成的误差进行分解，建立起对应的误差模型，进行视觉测量中的误差校正。

3 挠度测量相机消抖试验

为了验证笔者提出的相机抖动误差消除算法的有效性，进行了对于起重机主梁挠度的测量试验。门式起重机的主梁跨度为5 m，高度为4 m，额定载重为2 000 kg，试验现场如图8所示。其中两个参考点位于起重机主梁两边的端梁之上，端梁位置没有产生挠度变化，可以认为参考点固定不动，待测点位于起重机主梁跨中附近。

在该试验中，起重机的起吊重物为300 kg，通过加载、卸载和移动重物使主梁发生挠度变化。测量距离为20 m，在整个过程中，利用激光位移器和视觉挠度测量系统同步进行了一百次挠度值的采集。图9显示了两者测量结果的对比，同时也进行了视觉系统相机消抖前后挠度值的对比，可以看出，对相机抖动误差消除前，测量的挠度值和激光位移传感器的结果相差非常大，基本上没有重合点；而采用相机抖动误差消除算法后可以很好地消除由于相机抖动引起的挠度值的漂移、噪声和突变，相机消抖后的挠度和参考仪器测量的挠度值基本一致。

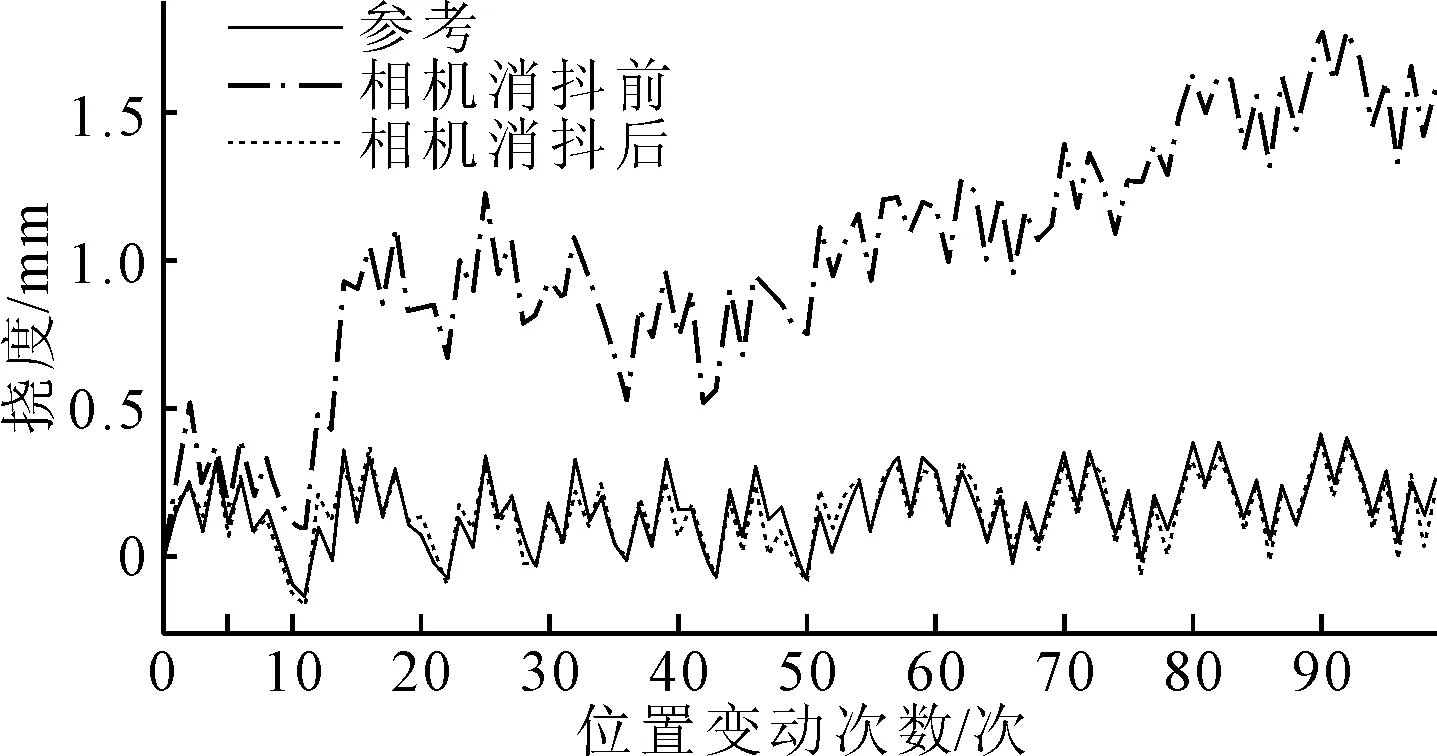
图9 挠度测量结果

表3为100次测量的均方根误差(RMSE)，相机消抖后为0.049 mm(1/33.24 pixel)，与相机消抖前相比，降低了97.92%。

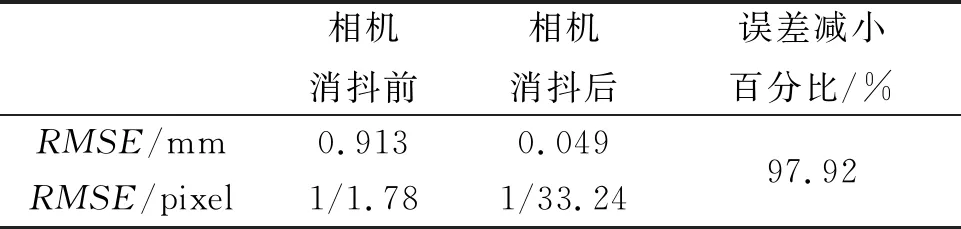
表3 挠度测量均方根误差

4 结论

试验表明，笔者所提出的视觉挠度测量系统中的相机抖动误差消除模型具有较好的效果，在远距离视觉测量领域具有较好的应用场景和研究价值。