T型槽织构化机床滑动导轨的摩擦学特性

朱 玮，吴玉国，时礼平,b,c，王 涛,b，章亦聪

(安徽工业大学a.机械工程学院；b.特殊服役环境的智能装备制造国际科技合作基地；c.特种重载机器人安徽省重点实验室，安徽马鞍山243032)

滑动导轨作为机床重要组成部分，具承载和导向作用，是保证机床精度的关键。导轨磨损是机床发生故障的主要原因，解决导轨磨损的传统方法有表面淬火和表面贴塑。表面淬火易导致导轨表面应力集中并产生较大的热变形[1]，表面贴塑会降低导轨导热性能和刚度[2]，淬火和贴塑均会造成导轨表面磨粒持续犁切的恶性循环。近年来，随着计算机技术、激光加工技术的发展，表面织构技术作为一种改善摩擦表面性能的方法，得到了国内外学者的普遍关注[3]。表面织构技术在轴承、活塞环等领域发挥了重要作用[4-6]。Hamilton等[7]研究发现，微织构可获得流体动压效应，减小摩擦系数，提高润滑性能；He等[8]将不同尺寸沟槽加工在聚二甲基硅氧烷(poly dimethylsiloxane，PDMS)材料表面，结果表明，沿平行沟槽方向运动时的摩擦系数高于沿垂直方向运动时的摩擦系数，且尺寸较小的沟槽能得到更低的摩擦系数；章亦聪等[9]提出一种莱洛三角形表面织构，并研究圆形、三角形、莱洛三角形织构密封端面的开启力、泄漏量和开漏比；魏伟等[10]数值模拟研究了单一螺旋槽、单一椭圆微孔和复合槽孔织构，发现复合槽孔织构具有较优的承载力、膜刚度和较小的泄漏量。

表面织构的摩擦性能与织构类型[11]、横截面形状[12]密切相关。Gu等[13]和Pei等[14]得出表面织构形状、尺寸对织构润滑减摩性能有很大影响，且存在最优的织构参数；Keller等[15]采用点接触往复实验研究灰铸铁上相同深度和宽度而不同间距的平行沟槽，发现在边界润滑区域，光滑表面和间距较大的沟槽表面摩擦系数较低；张赟等[16]利用激光加工技术在钢制导轨上制备4种微织构，发现所有微织构均可改善导轨副接触面的接触应力，且不同形状微织构的减摩能力不同；王国荣等[17]建立沟槽型表面织构化柱塞动压润滑理论模型，分析最小油膜厚度、织构深度、横截面形状、面积比及分布角度对柱塞密封副油膜承载力和摩擦系数的影响；李茂元等[18]利用数值模拟方法分析了直线槽截面形状和几何参数对平均压力的影响，得出Q型直线槽端面比普通R型直线槽端面具有更好的动压性能。综上研究发现：表面织构可有效改善端面摩擦性能，基本参数的变化对摩擦性能有较大影响。文中建立T型微沟槽织构化机床滑动导轨理论模型，借助数值模拟的方法考察T型槽织构长度系数比、宽度系数比、偏转角度、织构深度、进口速度对T型槽摩擦配副间无量纲承载力F、摩擦系数L和承摩比K的影响，以期为机床滑动导轨表面织构的设计和优化提供参考。

1 理论模型

1.1 几何模型

如图1 所示，导轨是由两个不接触的相对移动表面构成。其中：上表面为动轨；下表面为静轨；h0为润滑油膜厚度；hp为织构深度；u为动轨移速。

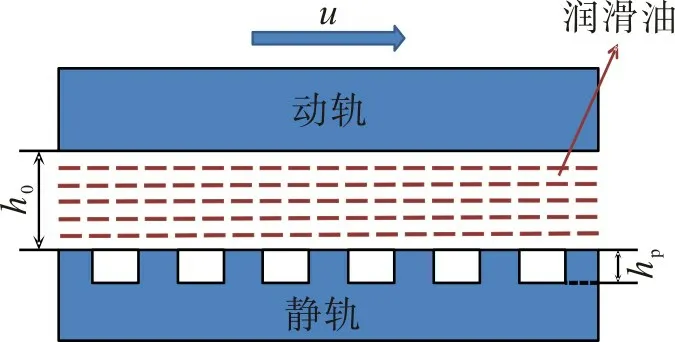
图1 导轨截面示意图Fig.1 Section diagram of guide rail

为方便研究，如图2所示，将织构化导轨表面以平面展开，并划分为单元区域，以此作为计算单元。除特别说明，织构延伸方向为y方向，进口速度方向为x方向。文中采用计算流体动力学数值模拟的方法，考察T 型槽的长度系数比α、宽度系数比β、偏转角度θ、织构厚度hp、进口速度u等参数对导轨T型槽摩擦配副间的无量纲承载力F、摩擦系数L和承摩比K等摩擦性能的影响。

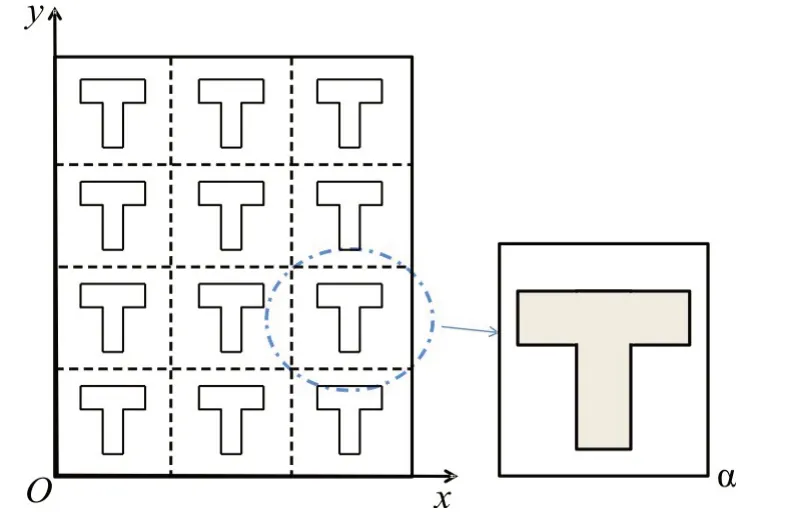
图2 静轨表面织构Fig.2 Surface texture of static rail

T 型槽基本结构如图3，为便于分析，将T 型槽长度系数比定义为ha/hb，记为α，即

T型槽宽度系数比定义为da/db，记为β，即

式中hb,db为定值。T型槽的偏转角度θ 定义如图4，逆时针方向为正方向。具体参数及取值范围如表1。

采用GAMBIT软件对T型槽内流体润滑膜进行网格划分，结果如图5。通过FLUENT软件设置二阶迎风格式对流体计算区域的承载力和摩擦系数进行求解。如图6所示，设置沿x 轴方向入口面为速度进口，y轴方向出口面为压力出口，两侧面为壁面，与织构接触的面为静壁面，与移动导轨接触的面为动壁面。整个过程中，忽略体积力作用；密封流体与壁面没有相对运动；密封流体为牛顿流体且不可压缩；不考虑温度、压力对黏度的影响；操作环境为恒温，定常层流；两端面间流体膜厚度处处相等；压力在膜厚方向处处相等。

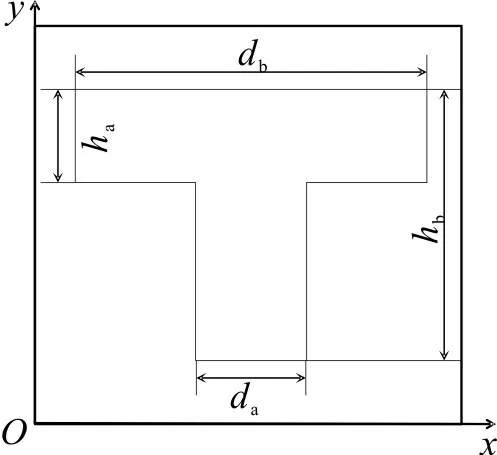
图3 T型槽的基本结构Fig.3 Basic structure of T-groove

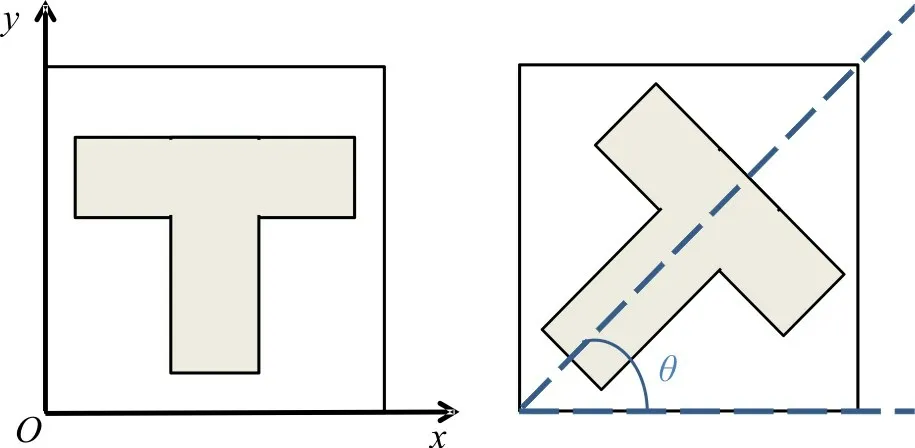
图4 偏转角度的定义Fig.4 Definition of deflection angle

图5 T型槽内流体润滑膜网格划分Fig.5 Mesh dixision of fluid lubrication film in T-groove

表1 规格及参数Tab.1 Specifications and parameters

1.2 数学模型

在流体动压润滑的条件下，基于流体润滑理论，采用只考虑流体动压效应稳态二维不可压缩Reynolds方程，表示为

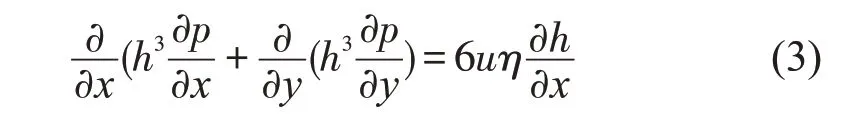
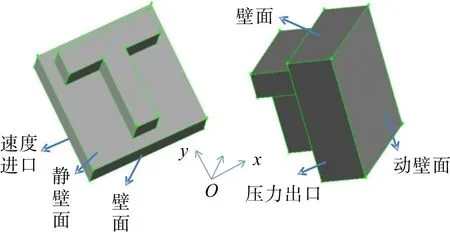
图6 计算单元边界条件Fig.6 Boundary conditions of the cell

式中：h 为润滑油膜厚度；p 为导轨表面压力；u 为两摩擦表面的相对速度；η 为流体介质的定常黏度。

织构化表面润滑油厚度为

周期边界条件

环境边界条件

式中：h0为最小油膜厚度；hp为织构深度；i,j 分别为x,y 方向的一个单元长度。

通过FLUENT软件对流体进行数值模拟，求得油膜承载力F(1/2)和摩擦系数L分别为：

式中：dxdy 为单位表面织构体微元；μ 为运动黏度。

无量纲承载力F定义为有织构时承载力F1与无织构时承载力F2的比值。

承摩比即为

2 结果与分析讨论

2.1 T型槽长度系数比对滑动导轨摩擦性能的影响

进口速度u=1 m/s、油膜厚度h0=10 μm、织构深度hp=10 μm、偏转角度θ=90°且在不同宽度系数比β的前提下，长度系数比α 对T 型槽织构化端面无量纲承载力、摩擦系数、承摩比的影响如图7。由图7(a)可知：随着长度系数比α 的增大，3种宽度系数比T型槽织构的无量纲承载力均呈先减小后增大的变化规律；α=0.3～0.4 时3 种织构的无量纲承载力较小，α=0.6 时3 种织构的无量纲承载力较大，表明α=0.3～0.4 时3 种织构的动压效应较差，α=0.6 时3 种织构的动压效应较好。由图7(b)可知：随着长度系数比α 的增大，3 种宽度系数比织构的摩擦系数均呈先减小后增大的变化规律；α=0.3～0.4 时3 种织构的摩擦系数较小，α=0.6 时3种织构的摩擦系数较大，表明α=0.3～0.4 时3种织构的摩擦性能较好，α=0.6 时3种织构的摩擦性能较差。由图7(c)可知：随着长度系数比α 的增大，3种宽度系数比织构的承摩比呈先增大后减小的变化规律；α=0.3～0.4 时3种织构的承摩比较大，α=0.6 时承摩比较小，表明在不同宽度系数比下，α=0.3～0.4 时3种织构的动压效应与摩擦性能较好，α=0.6 时3种织构的动压效应与摩擦性能较差。

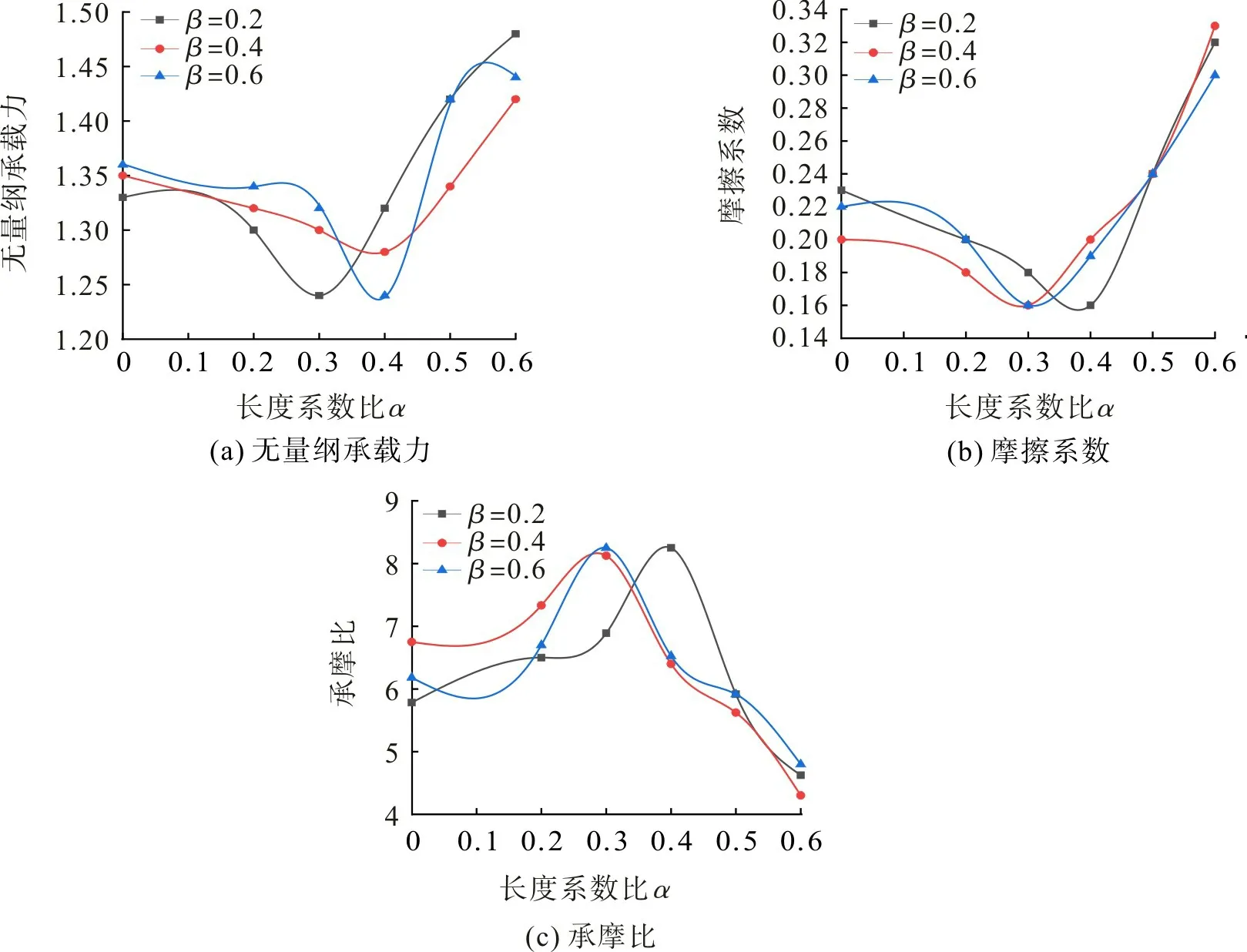
图7 长度系数比对T型槽织构化端面摩擦性能的影响Fig.7 Effect of length coefficient ratio on friction performance of the textured end face of T-groove

2.2 T型槽宽度系数比对滑动导轨摩擦性能的影响

进口速度u=1 m/s、油膜厚度h0=10 μm、织构深度hp=10 μm、偏转角度θ=90°且在不同长度系数比α的前提下，宽度系数比β 对T 型槽织构化端面无量纲承载力、摩擦系数、承摩比的影响如图8。由图8(a)可知，随着宽度系数比β 的增大，3种长度系数比T型槽织构的无量纲承载力均呈增大规律，表明随着宽度系数比β 的增大，3种织构均能取得较好的动压效应。由图8(b)可知：随着宽度系数比β 的增大，3种长度系数比织构的摩擦系数均呈先减小后增大的变化规律；β=0.5 时3种织构均具较好的摩擦性能。由图8(c)可知，随着宽度系数比β 的增大，3种长度系数比织构的承摩比均呈先增大后减小的变化规律；β=0.5 时3种织构承摩比均较大，表明β=0.5 时3种织构均具较好的动压效应和摩擦性能。

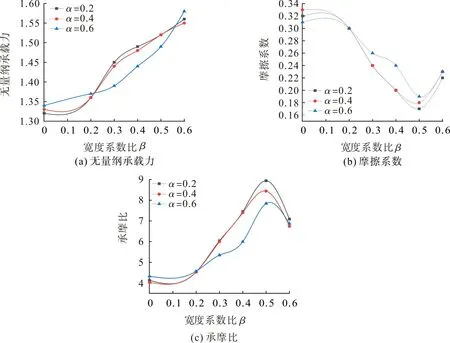
图8 宽度系数比对T型槽织构化端面摩擦性能的影响Fig.8 Effect of width coefficient ratio on friction performance of the textured end face of T-groove

2.3 T型槽偏转角度对滑动导轨摩擦性能的影响

进口速度u=1 m/s、油膜厚度h0=10 μm、织构深度hp=10 μm、宽度系数比β=0.4 且在不同长度系数比α 的前提下，偏转角度θ 对T型槽织构化端面无量纲承载力、摩擦系数、承摩比的影响如图9。由图9(a)可知：随着偏转角度θ 的增大，3 种长度系数比T 型槽织构的无量纲承载力均呈先增大后减小再增大的规律；θ=43°左右时3 种织构无量纲承载力较大，θ=90°时3 种织构无量纲承载力均最大；θ=0°～90°，α=0.6 的T型槽织构无量纲承载力均较大，表明α=0.6 的织构具有较好的动压效应。由图9(b)可知：随着偏转角度θ的增大，3种长度系数比织构的摩擦系数均呈先减小后增大再减小的变化规律；θ=45°左右均较小，θ=90°时均最小。由图9(c)可知：随着偏转角度θ 的增大，3种长度系数比织构的承摩比呈波浪式变化规律；θ=45°和θ=90°时较大，表明θ=45°和θ=90°时3种织构的端面均具较大的动压效应和良好的摩擦性能。

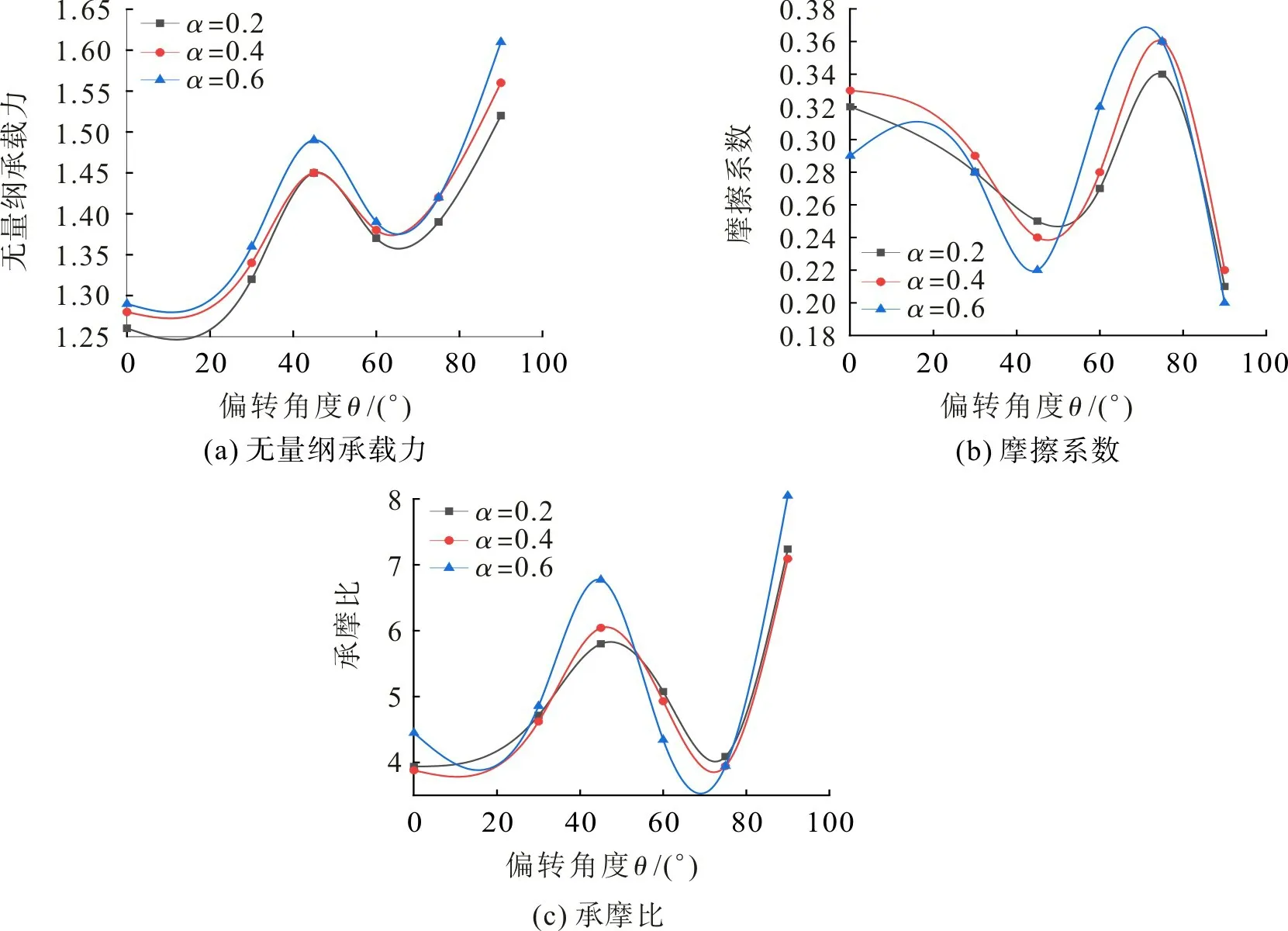
图9 偏转角度对T型槽织构化端面摩擦性能的影响Fig.9 Effect of deflection angle on friction performance of the textured end face of T-groove

2.4 T型槽织构深度对滑动导轨摩擦性能的影响

进口速度u=1 m/s、油膜厚度h0=10 μm、宽度系数比β=0.4、偏转角度θ=90°且在不同长度系数比α的前提下，织构深度hp对T 型槽织构化端面无量纲承载力、摩擦系数、承摩比的影响如图10。由图10(a)可知：随着织构深度hp的增大，3种长度系数比T型槽织构的无量纲承载力呈先略微增大后迅速减小的变化规律；hp=8 μm 时无量纲承载力均较大。由图10(b)可知：随着织构深度hp增大，3种长度系数比织构的摩擦系数变化规律与无量纲承载力相反；hp=6 μm 时达到较小值后迅速上升；α=0.2 的织构在整个过程中均具较小的摩擦系数，表明α=0.2 的织构具更好的摩擦性能。由图10(c)可知：随着织构深度hp增大，3种长度系数比织构的承摩比相互接近；hp=6 μm 时均较大，表明3种织构在hp=6 μm 时具良好的动压效应及摩擦性能。

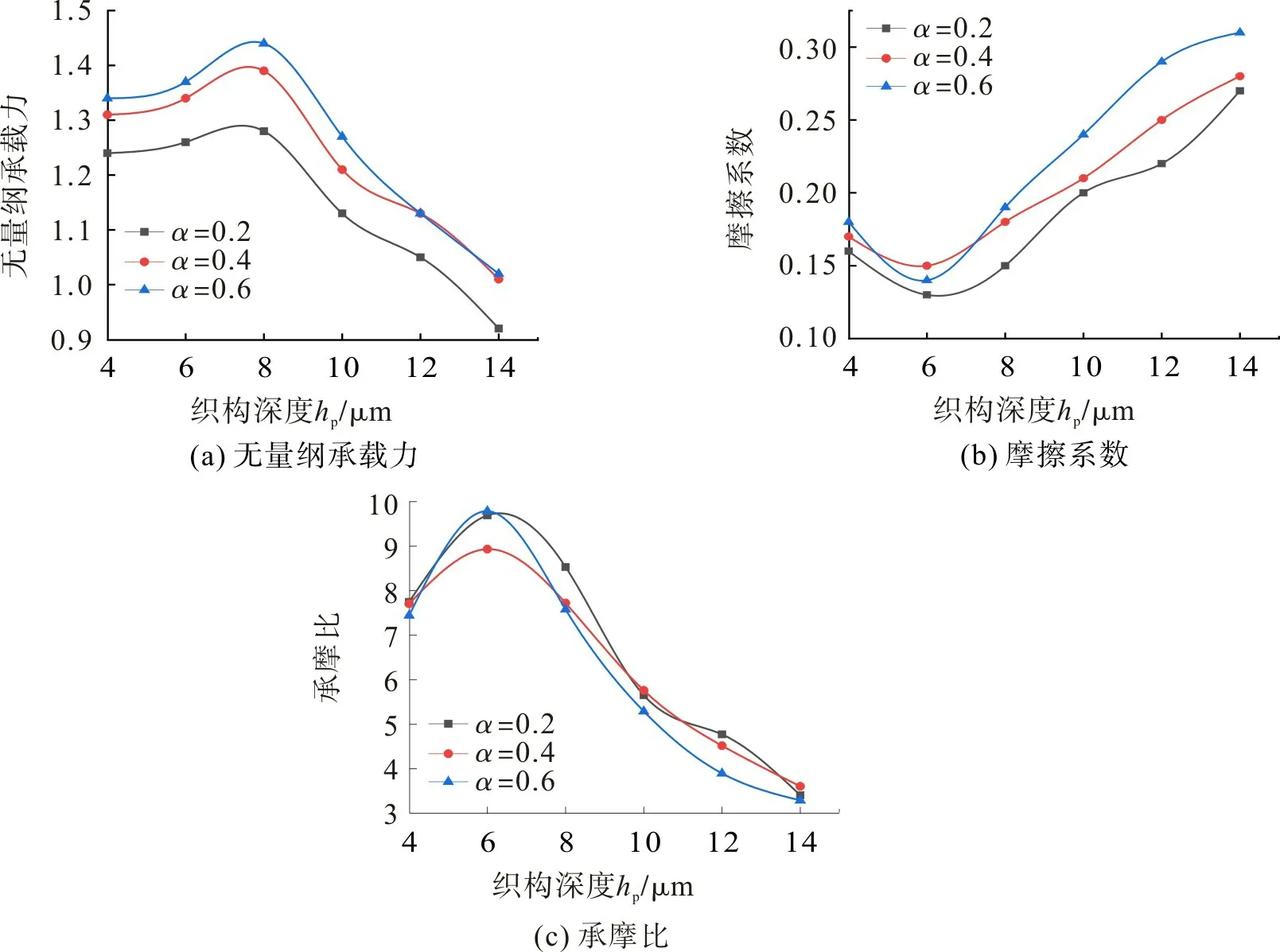
图10 织构深度对T型槽织构化端面摩擦性能的影响Fig.10 Effect of texture depth on friction performance of the textured end face of T-groove

2.5 T型槽进口速度对滑动导轨摩擦性能的影响

油膜厚度h0=10 μm、织构深度hp=10 μm、宽度系数比β=0.4、偏转角度θ=90°且在不同长度系数比α的前提下，进口速度u对T型槽织构化端面无量纲承载力、摩擦系数、承摩比的影响如图11。由图11(a)可知：随着进口速度u的增大，3种长度系数比T型槽织构的无量纲承载力均呈线性增大的变化规律；进口速度u相同时，α=0.6 的织构具较大的承载力及动压效应。由图11(b)可知：进口速度u对摩擦系数的影响与其对无量纲承载力的影响规律相似；随着进口速度u的增大，3种长度系数比T型槽织构的摩擦系数均呈不断增大的趋势；α=0.2 的织构具较小的摩擦系数和优异的摩擦性能。由图11(c)可知：随着进口速度u的增大，3种长度系数比T型槽织构的承摩比均呈不断增大的趋势；α=0.2 的织构具较大承摩比，表明较低进口速度与较小长度系数比的织构具更好的动压效应与摩擦性能。

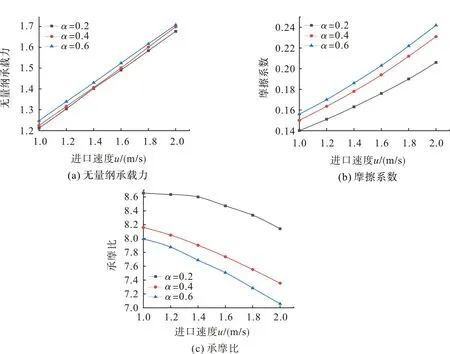
图11 进口速度对T型槽织构化端面摩擦性能的影响Fig.11 Effect of inlet velocity on friction performance of the textured end face of T-groove

3 结 论

建立T型槽表面织构化导轨端面的理论模型，研究T型槽织构的长度系数比α、宽度系数比β、偏转角度θ、织构深度hp、进口速度u对T型槽摩擦配副间摩擦特性的影响，得出以下结论：

1)随着长度系数比增大，不同宽度系数比T型槽表面织构化导轨端面的摩擦性能呈先增大后减小变化规律，文中条件参数下最优长度系数比α=0.3～0.4；最优宽度系数比与长度系数比呈相似规律，最优值出现在β=0.5 处；

2)偏转角度θ=45°和90°时，T型槽表面织构化导轨端面具更好的摩擦特性；

3)随着织构深度增大，T型槽表面织构化导轨端面的摩擦性能先增大后迅速减小，文中最优深度出现在hp=6 μm 左右；

4)增大T型槽织构进口速度会同时增大T型槽表面织构化导轨端面的无量纲承载力和摩擦系数，较小的进口速度会使T型槽表面织构化导轨端面的摩擦性能更好。