应用RBF 神经网络的订单完成时间（OCT）预测

王燕青，袁逸萍，李晓娟，李 明

（新疆大学机械工程学院，新疆 乌鲁木齐 830047）

1 引言

当前因社会经济和科技的发展，产品的质量、功能以及价格等特征之间的差异变得越来越小，客户转而日益关注交货时间，因此高效地针对顾客需求做出响应才能保持企业竞争力[1]。OCT是交货期的决定因素，OCT 预测成为车间管控的首要任务，此外精确的OCT 预测也是企业管理活动的需要，比如洽商合同[2]，协议制定[3]。“多品种小批量”已经成为现代生产的主流，以其为主要特征的制造企业通常以客户需求为中心，订单式生产。在制定订单交货期时，尽可能精准，否则若交货期估计太长，降低企业竞争力；估计太短，超出了企业的生产能力阈值，难以满足按时交货要求。订单的最终完工期决定了订单的交货期，因此，产品OCT 预测是制造企业面临的重要问题。

国内外许多专家学者就这个问题进行了研究，例如：文献[4]针对半导体制造系统的复杂性导致交货期预测的困难，科学地提出了建立订单式生产交货期线性回归预测模型的方法，并做了仿真和验证；文献[5]考虑模具制造过程的特殊性和返修产品不确定性，在此基础上利用利用马尔科夫理论模型推导出OCT 计算公式；文献[6]针对晶圆在制品数量众多以及生产周期长导致的复杂订单完工期预测问题，利用回归分析方法提取强相关变量实现了订单交货期的精准预测；文献[7]综合考虑各种对完工期有影响的因素，在最大化收益的条件下，建立交货期决策模型，实现对交货期的预测；文献[8]提出了基于BP 神经网络和历史数据的模具订单交货期决策方法；文献[9]考虑完工期的确定影响因素及随机影响因素并根据统计学方法，创建了完工期区间预测模型；文献[10]在机器故障情况下建立了模糊神经回归算法完工期预测模型，并验证此方法的简单和准确以及灵活性等特点；文献[2]通过分析订单完工期的影响因素，采用深度神经网络实现对完工期的预测，并通过实例验证此方法的可行性。

国内外专家学者就OCT 预测方面的研究取得了一定程度的进展，但仍然存在一些问题，主要体现在容易忽视车间的动态性，对于影响因素考虑不够全面等方面。

基于上述现状以及实时制造车间的复杂环境及其变量之间的非线性相关性，提出实时作业车间环境下应用RBF 神经网络的订单完成时间（OCT）预测方法，并证明了该方法的优越性。

2 影响因素的确定与量化

订单的完工期定义为在离散制造生产系统中从第一个制品开始进入系统到最后一个制品顺利下线的中间过程所花费的时间T，它受到车间实时负载S 和订单构成C 两个定性因素的影响。S 可以用某时刻设备前有多少待加工品来表示；C 则用可产品类型以及对应类型产品的数量来表示。

假设车间可生产M 种产品，有相应的加工设备N 台，需要某道工序的ni（i=1，2…N；ni=1，2…，M）种类型产品；订单由H 个产品组成，产品类型j 的数量为在某一制造设备i之前待加工产品的数量为W（ii=1，2……N），其中，产品类型j 的数量为这表明，总个变量是影响订单完工期的量化因素，即｛Q1，Q2，…，QM，W11，W12，…，W1n1，…，WMN｝，订单完工期的函数用F 表示，记作F=f（Q1，Q2，…，QM，W11，W12，…，W1n1，…，WMnN），由于函数f 的形式未知，只能采用机器学习的方法来建立影响因素与订单完工时间之间的关系。当加工设备M和产品类型N 比较大时影响因素数量也随之增大，一般模型在解决简单或很强的条件约束问题时是高效的，但是当应对复杂的实际问题时，就显得能力不足，比如会出现泛化能力差等问题[7]。考虑到企业实际生产过程中蕴含的复杂非线性关系和RBF 神经网络能够任意精度逼近所有非线性函数的优势，选用RBF 建立OCT 预测模型并进行预测。

建模和预测过程包括三个基本步骤：

（1）收集样本；利用FleXsim 系统构建仿真模型，采用蒙特卡罗方法随机生成若干组数据作为初始状态条件，通过运行仿真过程得到订单完工期，从而得到所需样本集；

（2）模型训练；采用60%样本集作为训练集来训练RBF 神经网络模型；

（3）预测并分析结果；使用剩余40%数据作为验证集合进行预测并分析结果。

3 样本收集

可以通过历史数据统计和模拟试验进行样本采集。由于仿真试验方法能真实模拟实际生产过程且可避免“脏”数据的影响，因此利用这种方法来收集样本数据。FlexSim 是一个面向对象的仿真环境，使用FlexSim 平台创建离散事件过程，如制造，物料处理场景都配以极相似的3D 虚拟现实环境。其基本构成元素包括发生器、处理器、暂存器、吸收器等实体以及相关临时实体，用户能自定义临时实体的结构类型，以及相关参数设置。

以下三个假定条件是仿真模型的构建和运转的前提条件：

（1）待加工工件的加工顺序服从“先来先服务”的原则，为简化问题这里不考虑工件加工的优先级；（2）已知每种产品的详细工艺参数，包括在不同设备的加工顺序和在某固定设备上的平均加工时间；（3）不考虑紧急插单、设备故障、人员缺勤等不确定因素。

一个基于FlexSim 平台的离散制造车间仿真模型的一个实例，如图1 所示。其中，处理器代表车间加工设备（从左往右依次分成五组）；暂存区（与每一组处理器相对应）代表加工设备前的待加工区域，其Box 数量代表待加工产品的总数量；发生器代表订单来源，分别对应三种在制品类型，实体之间的连接线表示加工工艺路线。通过随机设置发生器中不同在制品订单数量来记录不同暂存区中不同类型产品的等待加工数量，从而获取数据样本。

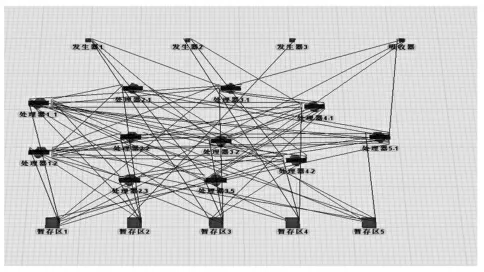
图1 应用FlexSim 平台的车间仿真模型Fig.1 Workshop Simulation Model Based on FlexSim Platform

在FlexSim 仿真系统上二次开发得到的界面，如图2 所示。

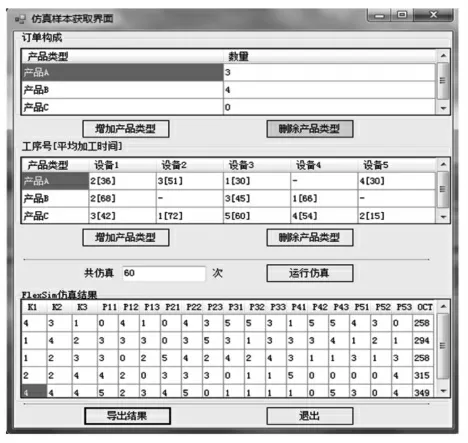
图2 二次开发界面Fig.2 Secondary Development Interface

其主要功能包括：

（1）通过蒙特卡罗随机模拟方法自动生成若干数据，构成仿真初始状态样本集；（2）将上述数据自动应用到仿真中，作为仿真模型的初始状态；（3）仿真结束获取订单的完工期（OCT）；（4）循环执行步骤（2）、（3），得到一定容量的样本集。

4 RBF 神经网络模型

RBF 神经网络具有很强的鲁棒性、强大的自学习能力以及非线性映射能力，可以逼近任意的非线性函数，具有很强的应用市场。因此，选择RBF 神经网络模型进行OCT 预测，具体的算法步骤如下：

（1）对FlexSim 仿真平台获取的数据进行数据过滤以及数据归一化处理，筛除不良数据，去除量纲影响；

（2）通过分析确定影响模型性能的几个重要参数；

（3）通过实验确定若干参数的相应最优取值，明确最终RBF神经网络模型；

（4）选取几个典型机器学习模型，进行上诉分析，确定模型最优参数；

（5）运行上诉算法以及相应对照模型，进行结果分析。相应算法流程，如图3 所示。

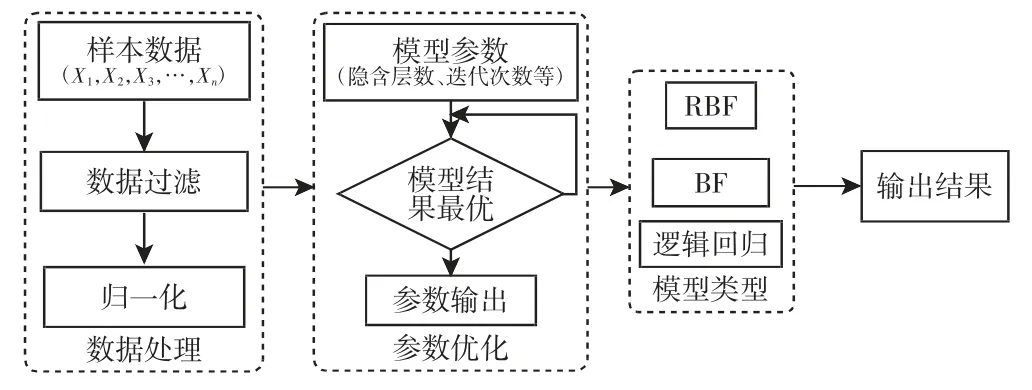
图3 算法流程图Fig.3 Algorithm Flowchart

4.1 数据标准化

为去除不同数据间的不同量纲对于运行结果的影响，需进行归一化操作。假设有N 个样本，OCT 预测样本矩阵XNx19，即：

式中：Xi，1，Xi，2，…，Xi，19—第i 个样本的对应订单构成以及等待加工序列的取值。标准化处理得到标准矩阵，即：

4.2 RBF 神经网络

模型标底预测模型的激活函数选用高斯函数，公式如下：

式中：‖·‖，c，σ—欧式范数，高斯函数的中心以及方差。此时，RBF 预测模型的输出由隐含层各输出值进行加权得到，其公式：

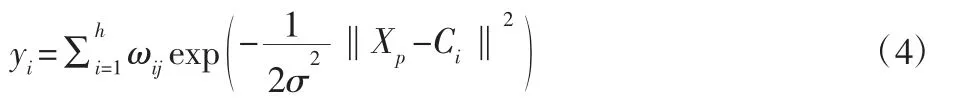
式中：xp—第p 个输入样本，p=1，2，…，P，共有P 个输入样本；ci—隐含层结点的中心；wij—连接权重值，i=1，2，…，h，对应于隐含层的每个结点，j=1，2，…，n，为输出层每个结点；yj—相应样本的输出。以基于K－均值聚类法求c，进而求解方差σ，方差为：

式中：i＝1，2，…，h；cmax—的选择中心的最大距离。

求解wij时用最小二乘法，其算法为：

其中，p=1，2，…，P；i=1，2，…，h。

5 实例验证

5.1 问题描述

一个制造车间由E1、E2、E3、E4、E5五组机器组成，分别包含3，2，4，3，1 台相同的机器。可生产三种产品分别为A、B、C，分别需要4、3 和5 道工序，每个工序必须在规定的机器上按照预定的工序顺序进行加工。其中，A 产品工艺路线为E3→E1→E2→E5，B产品工艺路线为E4→E1→E3，C 产品工艺路线为E2→E5→E1→E4→E3。例如产品C 分别在分别在E2、E5、E1、E4、E3机器组上加工，首先在E2机器上加工，加工时间为72；然后在E5机器上加工，加工时间为15；而后在E1机器上加工，加工时间为42；再在E4机器上加工，加工时间为54；最后在E3机器上加工，加工时间为60，如表1 所示。如果一个产品到达生产系统，发现所有的机器都处于工作状态，那么在机器组中产品遵循FIFO 规则队列。

表1 原料加工工艺路线与各工序加工时间参数Tab.1 PRaw Material Processing Route and Processing Time Parameters of Each Process

在FlexSim 平台上构建的仿真模型，如图1 所示。通过运行仿真模型得到一组样本数据，样本容量为60，样本，如表2 所示。（只列出部分数据）。以第二个样本个体为例，表示包括7 个产品的某个订单（产品类型A 的数量为1，B 的数量为4，C 的数量为2），在实时状态S（设备组E1前有3 个A 产品3 个B 产品和3 个C 产品等待加工，设备组E2前有3 个B 产品和5 个C 产品，设备组E3前有3 个A 产品和1 个B 产品和3 个B 产品，设备组E4前有3 个A 产品3 个B 产品和4 个C 产品，设备组E5前有1 个A 产品2 个B 产品和1 个C 产品）条件下，该订单的完工期为294（仿真结果），仿真结果最终导出成MATLAB 可以读取的Excel 类型文件。

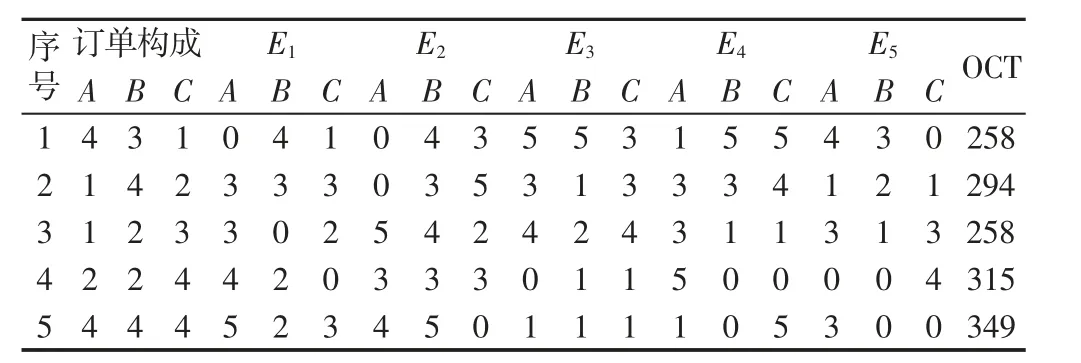
表2 订单完工期仿真样本Tab.2 Simulation Sample of Order Completion

5.2 实验验证

建立RBF 神经网络预测模型，其基函数为高斯函数，并在MATLAB 2014a 平台上进行了仿真验证。

部分代码如下：

由训练经验可得，初始化学习精度ε 为0.01，最大隐含层神经元数为57，扩展常数spread 定为3，网络模型为21-57-1，模型的输入节点数为21，输出节点数为1，训练完成后分别预测剩余30%的，从FlexSim 仿真数据中随机选取60%的数据作为RBF 神经网络模型的训练集，余下的40%作为模型的测试集用于验证样本的OCT 可靠性及其结果分析。

5.3 结果分析

为了进一步验RBF 神经网络在解决本问题上的优越性能，选取另外两种常用的机器学习算法，各进行10 次实验，选取其最优的结果与RBF 神经网络的性能对比，更清楚地表明了RBF 神经网络的优越性，如图4～图6 所示。

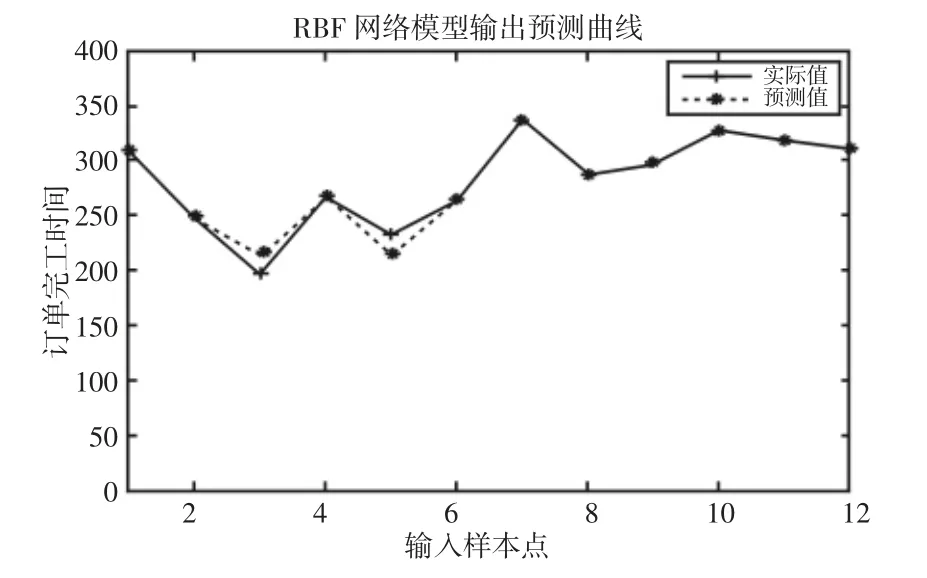
图4 RBF 网络模型输出预测曲线Fig.4 Output Prediction Curve of RBF network

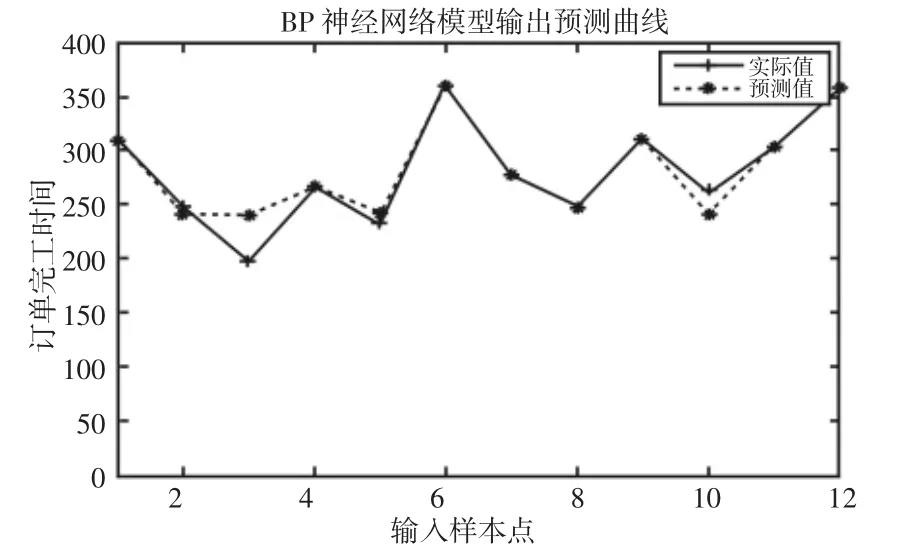
图5 BP 神经网络模型输出预测曲线Fig.5 Output Prediction Curve of BP network

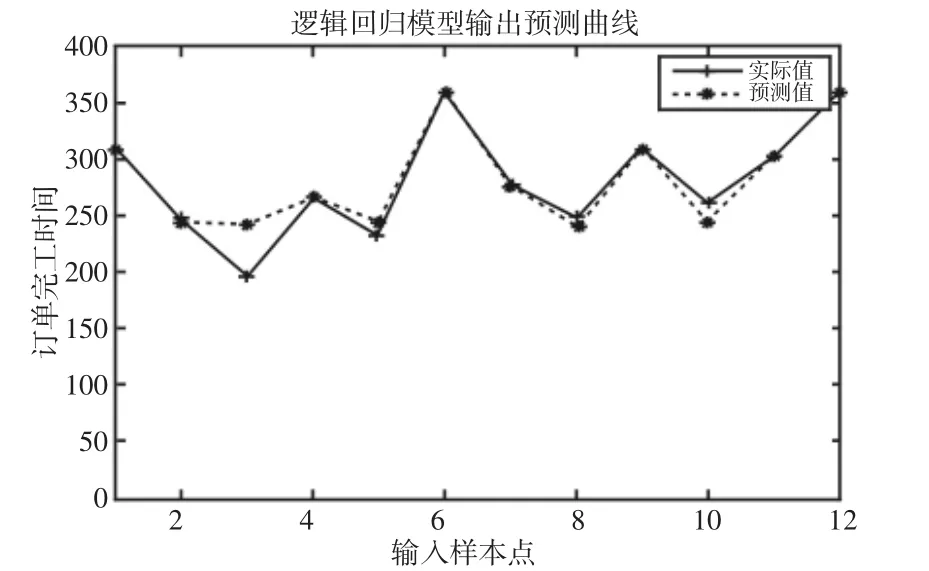
图6 逻辑回归模型输出预测曲线Fig.6 Output Prediction Curve of Logistic Regression

选取SSE（累积方差），MSE（均方差），MV（相对误差均值）作为评价分析指标，对比结果，如表3 所示。

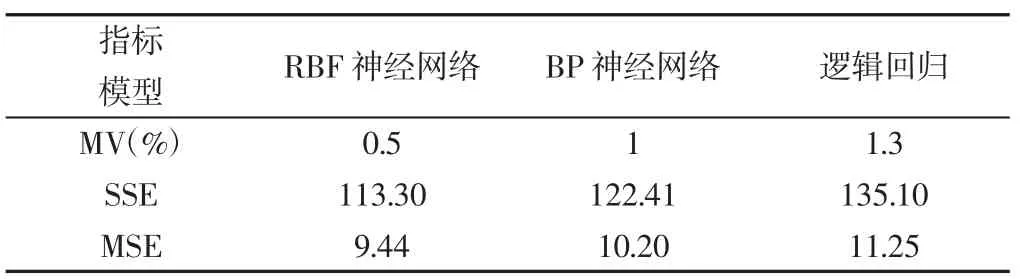
表3 分析指标对比结果Tab.3 The Result of Analysis Index Comparison

由以上结果分析，BP 神经网络，逻辑回归，RBF 神经网络三种模型都可以进行订单完成时间的预测，但是BP 神经网络的累计方差达到了122.41，逻辑回归模型达到了135.10 均大于RBF神经网络运行结果，另外相对误差均值也有同样现象，综上分析RBF 神经网络运行精度更好，优越性更强。通过预测结果与仿真结果的比较，证明该方法可以得到较为理想的订单完成时间预测结果。