自适应阈值在机电作动系统故障检测中的应用

杨建忠，贾海文，孙晓哲

（中国民航大学天津市民用航空器适航与维修重点实验室，天津300300）

1 引言

随着机电作动系统（EMA）的应用，去除了飞机上大量的液压回路，有利于飞机维修和减轻了飞机重量[1]。然而，新的故障和安全性的不足阻碍了EMA 在主飞行控制执行机构中的大量使用[2]。依据Moog 公司提供的故障模式，影响和关键性分析（FMECA 故障模式及影响分析）信息[3-4]、美国军方发布的工业信息和执行器相关故障文献追踪[5]，将机电作动系统故障模式分为：传动机构故障、驱动电机故障和传感器故障。

针对以上故障模式，国内外学者分别基于不同方法进行了故障检测。2016 年文献[6]提出了一种新的基于振动的混合技术，用于检测EMA 滚珠丝杠卡阻和滚珠碎裂故障，主要是通过比较丝杠健康理论值与EMA 测试台实验值进行比较。从而判断故障是否发生。文献[7]研究了基于EMA 的“数据驱动故障检测技术”在EMA 滚珠丝杠中设置两种不同剥落尺寸的剥落断层，使用贝叶斯分类器通过振动和电流两个条件指标来识别故障。文献[8]开发了基于EMA 的故障检测和量化技术，直接检查在测试台上收集的振动数据，以确定和表征健康状况，确定对振动数据执行高分辨率角度重采样（以消除速度波动）使得可以检测和测量EMA 滚珠轴承中的剥落的严重性。然而，上述检测方法虽然具有一定的有效性，但对各种扰动比较敏感，例如，操作条件，数据的扰动和传感器的测量，将会限制其在航空航天领域的应用。

文献[9]结合基于模型的故障检测神经网络技术与FFT 分析技术，对电机绕阻短路故障和转子静态偏心故障进行检测。文献[10]通过应用离散小波变换（DWT）监测PMSM（永磁同步电机）电流，来检测和诊断电气（短路：相与地之间或相与相之间）和机械（偏心）故障。虽然，傅立叶变换（STFT）等技术可以对不同的频率和时间进行分析，但其仅适用于系统处于稳态的时候。而在真实飞行状态中，EMA 工作在一个非稳态环境中，所以在检测时只能依赖于小波分析。然而基于信号处理的方法在飞机上的应用误报警率比较高。

针对EMA 传感器故障，文献[11]设计了一种基于Z 检验的故障检测程序来实现角位移传感器的自我诊断，并且通过卡尔曼滤波估计调整解算器的不匹配故障来实现故障调节，但并没有考虑噪声和外部干扰。2009 年文献[12]研究了传感器的不同故障模式，并设计了基于人工神经网络（ANN）的诊断系统。该方法不仅可以检测各种故障模式，而且可以区分传感器和系统故障。最后通过在机电作动器已有的实验数据中注入偏置、漂移、缩放等故障模拟来检测该方法的有效性。不足之处是，专家系统需要强大的数据支持和丰富的维修经验，而机电作动系统在民机上的应用属于一个全新的领域，使用时间和应用范围有限，所以基于专家系统故障检测方案还需要不断的完善。

考虑国内外有关机电作动系统故障检测的不足之处，采用了未知输入观测器，把建模的不确定性、外部干扰和测量噪声看作是系统的未知输入，使其从残差中完全解耦[13]。之后提出自适应阈值方法，利用数理统计中置信区间的思想来对残差动态范围进行区间估计，从而降低漏检率和误报警率[14]。

2 机电作动系统建模与故障建模

所研究的无刷直流电机为二相导通星形三相六状态[15]。

2.1 电压平衡方程

无刷直流电机三相电流满足iA+iB+iC=0；绕组自感满足LA=LB=LC=L；互感满足MAB=MBA=MBC=MCB=MAC=MCA=M；无刷直流电机绕组任意一项电压可表示为因此无刷直流电机三相绕组相电压方程为：

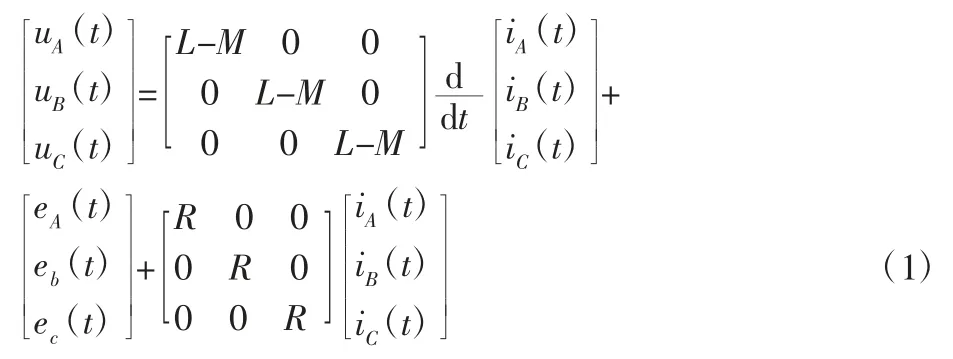
式中：UA（t），UB（t），UC（t）—绕组相电压（V）；eA（（t），eB（（t），eC（（t）—绕组反电势（V）；iA（t），iB（t），iC（t）—绕组相电流（I）；R—相电阻（Ω）；L—绕组自感（H）；M—绕组互感（H），且L-M>0；

2.2 转矩方程

电机运行时，电源产生的电功率除小部分转化为铜耗和铁耗外，大部分通过气隙磁场把转子永磁体的力矩传递给转子，这部分功率为电磁功率，电磁功率满足Pε=eAiA+eBiB+eCiC；不计转子的机械损耗和杂散损耗，电磁功率全部转化为转子动能，因此，Pε，则机电作动器转矩方程为：

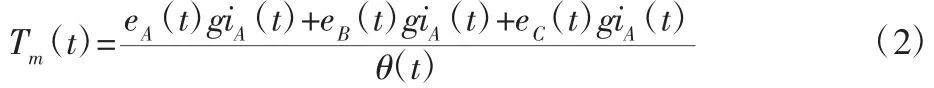
式中：Tm（t）—电机的电磁转矩—电机转子角速度。

2.3 运动方程

要构建机电系统完整微分方程的数学模型，还需引入机电作动器运动方程为：

基于上述方程，建立机电作动系统状态方程如下：

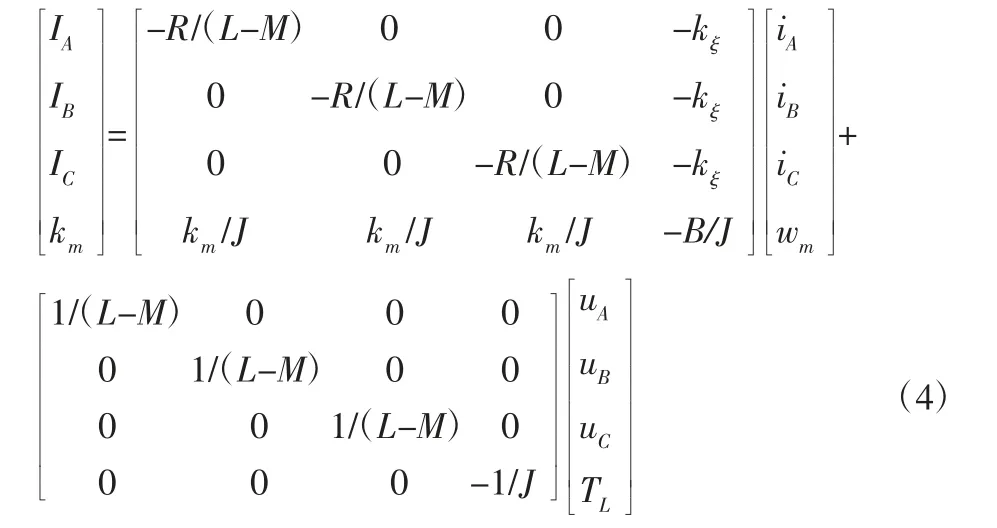
式中：i—电机母线电流；wm—电机转速；x—舵面位移。

为了简化计算步骤，系统状态用母线电流代替。因为对无刷直流电机每一相导通的电枢绕组而言，其反电动势和电磁转矩生成的原理和过程与传统有刷直流电机完全类似，分析过程也相似，所以式（4）可以改为如下状态方程。系统参数，如表1 所示。

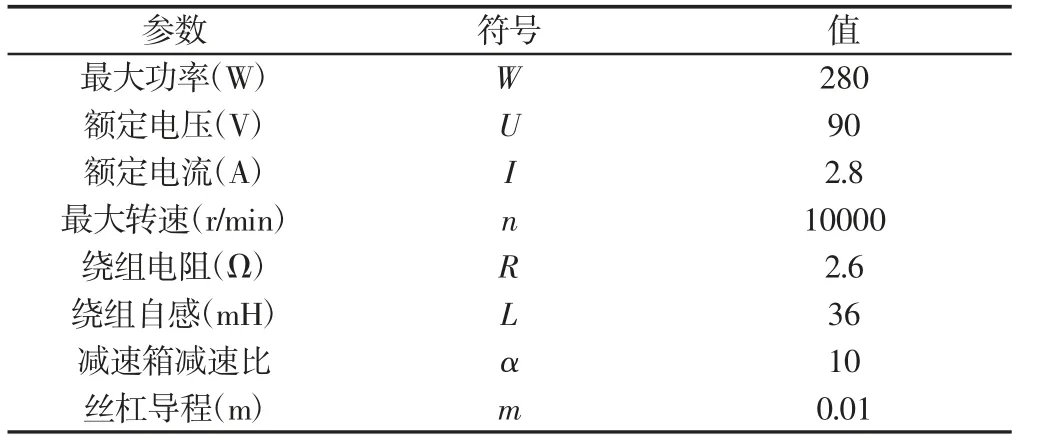
表1 系统参数Tab.1 System Parameters

代入上述参数得：

3 观测模型推导

考虑外界干扰和模型不确定性的影响是实际故障检测算法中一个重要的考虑因素。针对此类问题，采用未知输入观测器，通过参数设计完全解耦干扰。

3.1 未知输入观测器（UIOS）

观测器的结构可描述为：

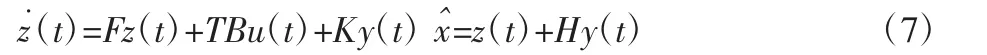
式中：u∈R2—系统的输入向量；y∈R3—可测输出向量；—状态矢量估计值；z（t）—该观测器的状态（等效于x（t））；F、T、K、H 是待设计矩阵，结构如图1 所示。

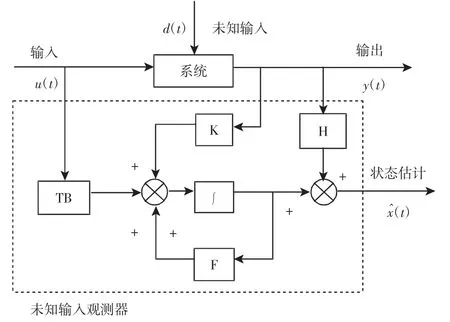
图1 未知输入观测器Fig.1 Unknown Input Observer

以如下系统为例：

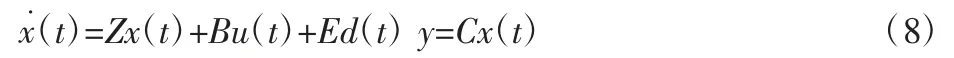
式中：x∈R3—系统的状态向量；u∈R2—输入向量；y∈R3—可测输出向量。d（t）—未知输入信号，代表外界干扰和建模不确定性。矩阵A、B、C、E 是具有相应维数的常数矩阵。将观测器（7）用于系统（8）时，状态估计误差为由下列方程控制：得：

如果使：

那么状态估计误差为：

如果F 具有全部稳定的特征值，e（t）将渐进收敛于零。基于以上思路，建立机电作动系统未知输入观测器，首先干扰分布矩阵设为：

通过式（10）可以计算得出：

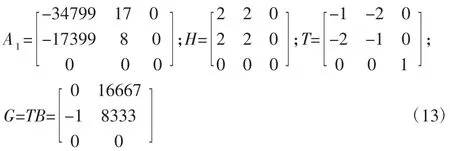
配置F=A1－K1C 极点为［-34755-9-30］，得：

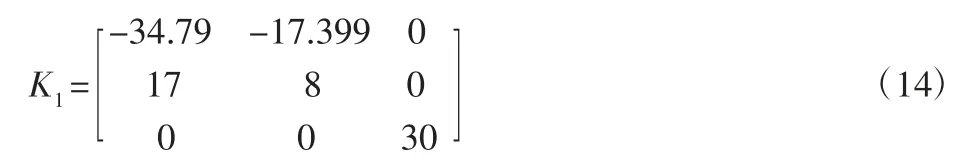
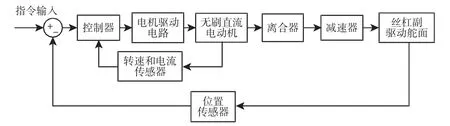
图2 机电作动系统Fig.2 Electromechanical Actuation System

得机电作动系统未知输入观测器，之后应用于机电作动系统。系统包括指令发送模块、无刷直流电机本体模块、机械传动装置和飞机舵面模块。机电作动系统采用三闭环控制：转速环和位置环采用PID 调节器，电流环采用电流滞环调节器，如图2 所示。电机参数表1 已经给出。

3.2 EMA 三闭环模型验证

基于实验室EMA 半物理试验平台，提取EMA 测试平台输入/输出试验数据，通过系统辨识得到试验平台传递函数（输入为舵面指令，输出为舵面的实际位置）如下：

基于相同输入比较以上传递函数与系统模型的动态响应，来验证建模的准确性：采用阶跃/斜坡两种不同的输入，负载一致，如图3、图4 所示。

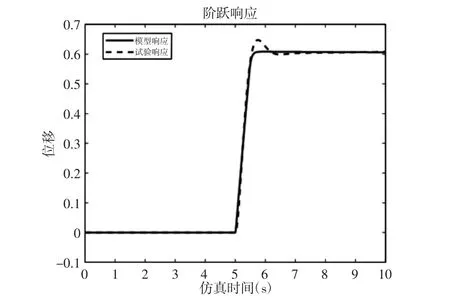
图3 阶跃输入Fig.3 Step Input

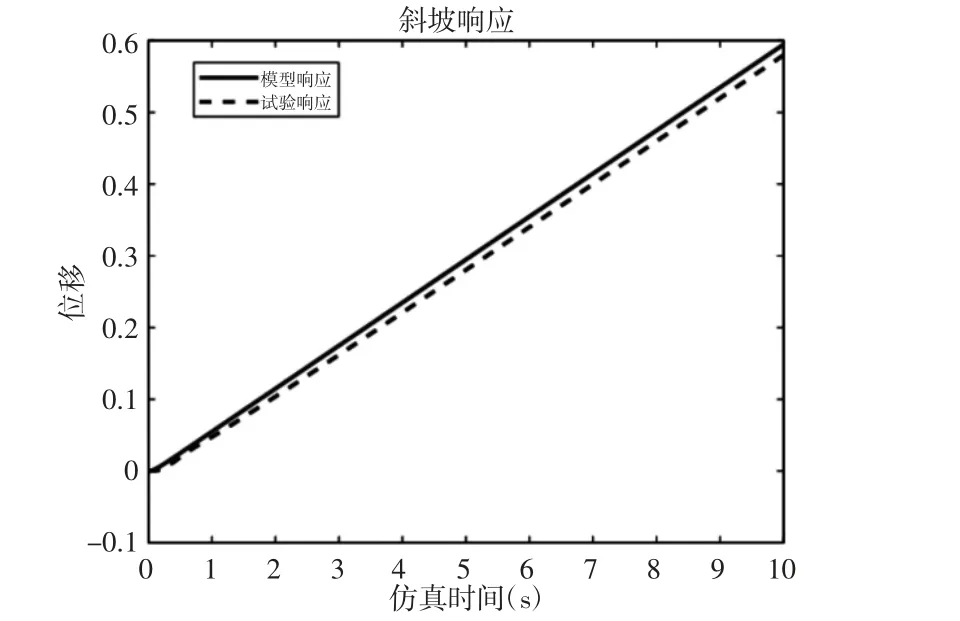
图4 斜坡输入Fig.4 Ramp Input

从上图可以看出，对于不同的输入，机电作动系统模型和试验台的位移响应基本一致，从而验证的模型的准确性。

3.3 故障注入

传感器出现故障时，会损害系统的总体性能，因此传感器对于确保机电作动系统最佳性能和安全性方面发挥着至关重要的作用，但是其故障特征往往会被系统动力学和外部干扰所掩盖，因次对该故障检测具有一定的难度[16]。对于系统电机绕组短路故障，由于系统控制器的作用，故障发生时，实际舵面偏角依然会调跟随指令信号，不会表现出故障现象，但是如果不及时采取措施，某相绕组持续发热，最终会烧毁电机[17]。因此，以传感器故障和电机绕阻故障为例，来验证故障检测算法的有效性。

3.3.1 电机绕阻故障

假设电动机a 相绕组短路时，a 相电阻、电感为零。仿真结果如图5 所示。

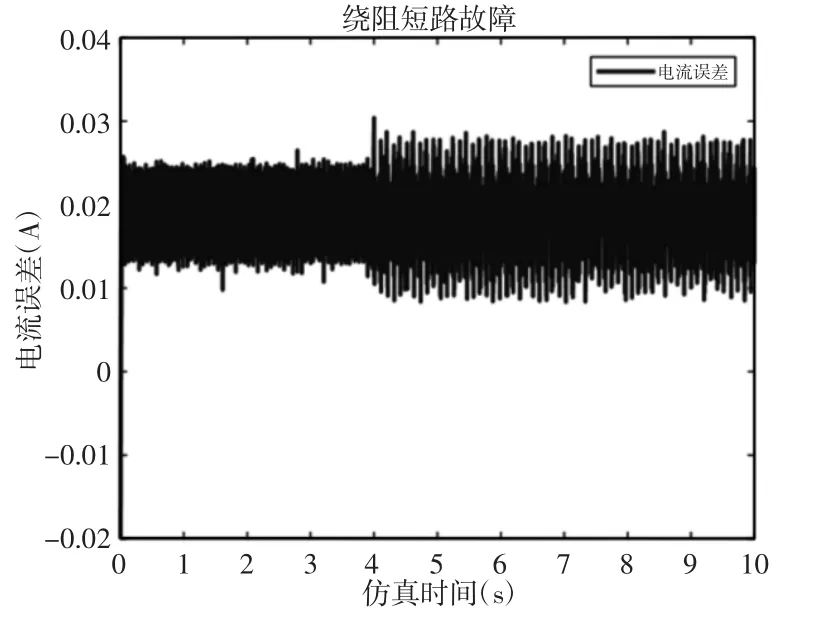
图5 绕阻短路故障Fig.5 Winding Short Circuit Fault

从图5 可以看出，在第4s 电机单向绕阻出现短路故障，导致未知输入观测器与系统输出偏差增大。

3.3.2 传感器偏置故障

在系统位置传感器发生故障时，系统得到的位置反馈信号并非准确值，而是传感器受到干扰的信号或错误信号。因此，可以在信号反馈处增加一个恒值偏差Δx 模拟偏置故障：Δx=0.01（正常值的5%），仿真结果，如图6 所示。

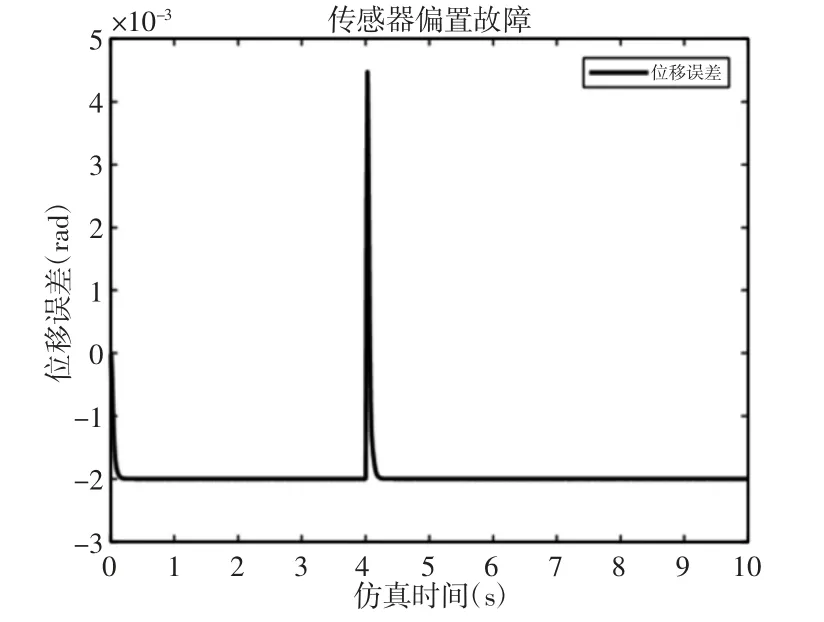
图6 传感器偏置故障Fig.6 Sensor Bias Fault

从图6 可以看出，在第4s 机电作动系统位置反馈传感器发生偏置故障，未知输入观测器与系统输出偏差明显增大。以上结果证明观测器设计满足要求可以有效判断故障是否发生。

3.4 自适应阈值

对于机电作动系统，当出现突变故障时，残差变化明显，可以直接用固定阈值进行故障判别。然而，对于丝杠磨损、电机绕阻短路、传感器恒增益变化等类似故障都属于缓变故障（故障以一定的斜率变化）[18]，在故障的早期阶段，故障特征不明显，再加上外部干扰、测量噪声和建模的不确定性，往往会造成故障漏检。此外当飞机做高速运动时，会造成传感器信号的突增，导致故障误检测。因此，为了尽可能在故障发生的早期就能将故障检测出来，同时降低误报警率，通过对残差（系统输出与观测器输出的差值）的统计特性进行研究，将统计学参数置信区间估计的思想应用于自适应阈值设计。

考虑机电作动系统的残差是一个非平稳的随机过程，但近似于高斯分布[14]。考虑到残差随未知输入幅值的变化，残差的均值和方差可以根据统计学原理来表示。其中残差的均方根、均值和方差求取方法分别为：

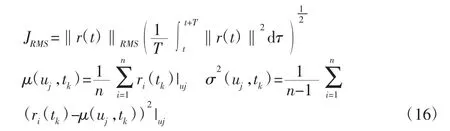
置信度为（1－α）的均值的置信区间可表示为：

式中：α—置信水平；z—与置信水平相关的系数。在实际应用中，置信度（1－α）通常选为（95～99）%。当置信度为95%，则z 为1.96，由式（18）可求得阈值为：

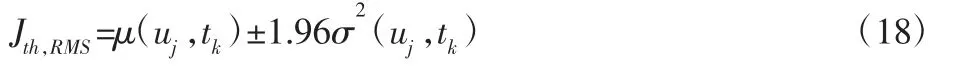
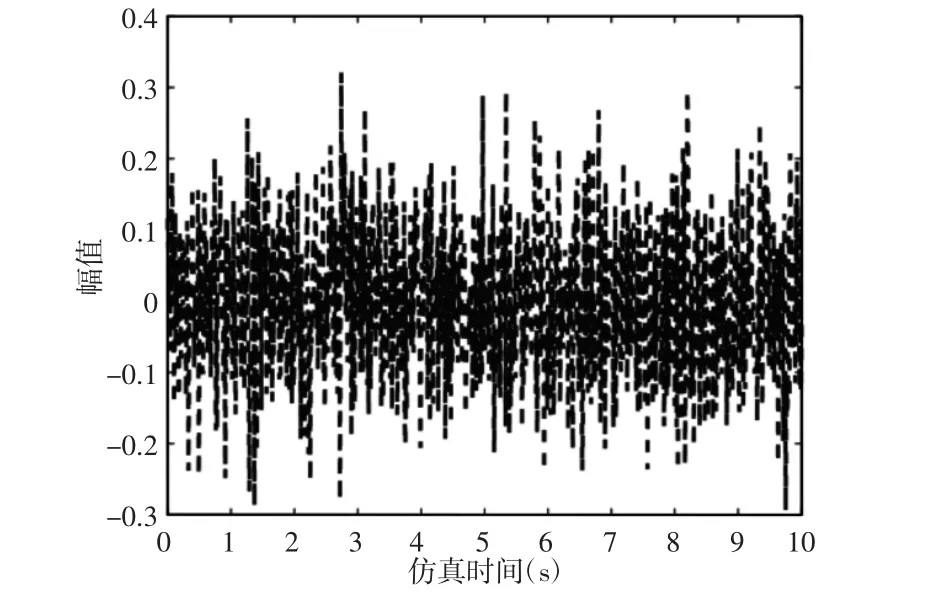
图7 测量噪声Fig.7 Measurement Noise

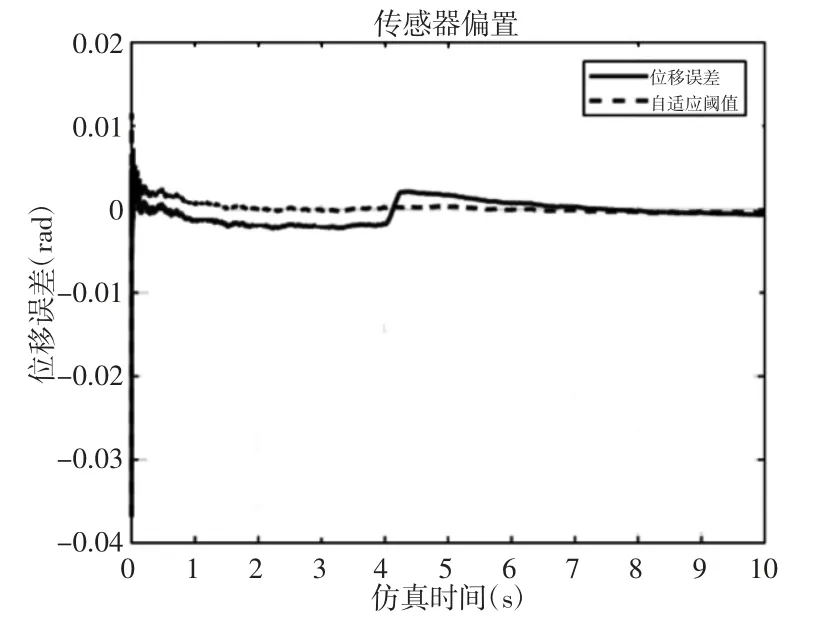
图8 传感器故障Fig.8 Sensor Failure

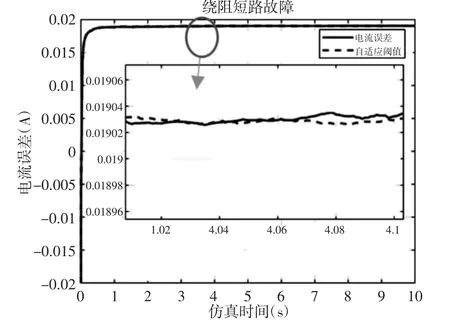
图9 绕阻短路故障Fig.9 Winding Short Circuit Fault

当残差的均方根（RMS）超过式（18）计算的阈值时，发出报警信号，表示系统发生了异常。这里的任务就是在残差的均方根（RMS）刚超过该阈值的时候，将其检测出来。本节依然对上述故障进行仿真，仿真通过在Simulink 中实现，仿真参数与注入时间不变，仿真中采用的测量噪声，如图7 所示。故障检测仿真结果，如图8、图9 所示。

从图9 可以看出，当舵面负载比较小时，电机绕阻短路故障对电流的影响会很小，此时很难通过固定阈值去判断故障是否发生，阈值选取不当就会造成误报或者漏报。但是，自适应阈值可以在故障发生早期检测出绕阻短路故障的发生。

为了评估自适应阈值检测方案的性能，将电机绕阻故障和传感器偏置故障分别加入系统中。同时设计固定阈值和自适应阈值，然后根据故障发生时间和故障程度来比较它们的性能，其中传感器偏置故障的失效范围[19]，如表2 所示。这里传感器偏置故障选取第4s 时正常值的30%和60%，固定阈值设置为0.0116，即图10 中残差的最大值加一个微小常量，固定阈值与自适应阈值对比结果，如图11 所示。

表2 传感器偏置典型范围Tab.2 Typical Range of Sensor Bias

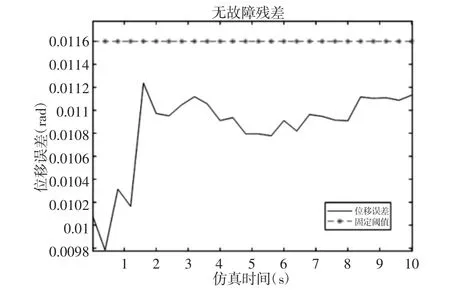
图10 无故障系统残差Fig.10 Fault－Free System Residuals

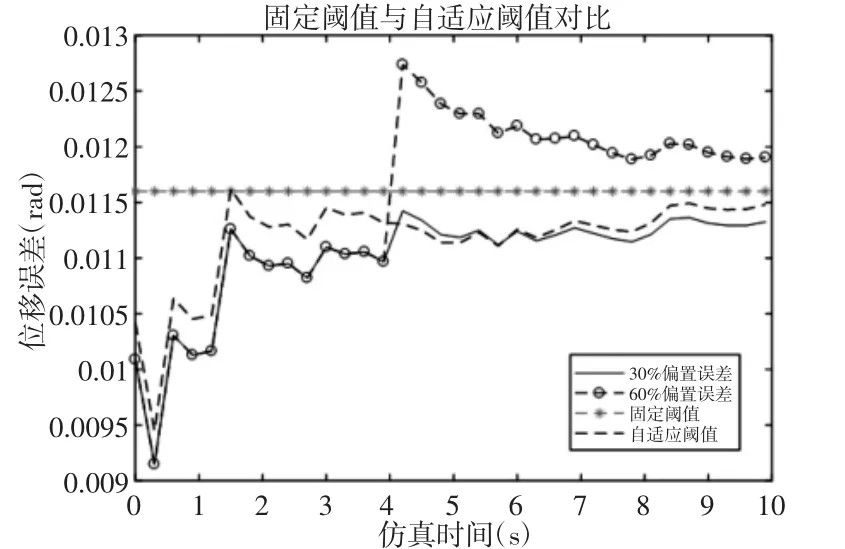
图11 传感器位移偏置故障Fig.11 Sensor Displacement Bias Fault

图11 比较了自适应阈值与使用固定阈值关于传感器偏置故障的检测结果。可以看出，当测量噪声比较大时，固定阈值设置会增大，导致位移偏置30%时，会出现漏检。相比而言，自适应阈值可识别故障，在故障早期，故障程度比较微弱的情况下，自适应阈值对故障的灵敏度起到了故障预测的效果。为了验证其鲁棒性，在系统无故障状态下加入一个短时脉冲（第4s 加入，持续时间为0.4s），仿真结果，如图12 所示。可以看出在正常情况下，固定阈值在大脉冲瞬时阶段会产生虚假报警，而自适应阈值的设计考虑了测量噪声和模型不确定性，提高了监测性能和检测灵敏度，降低了误报警率。电机绕阻短路故障检测情况，如图13 所示。可以看出，从第4s 故障发生到超出固定阈值的时间远远大于自适应阈值检测的时间，从而证明了自适应阈值对故障的灵敏度更高，可以更早的检测到故障。

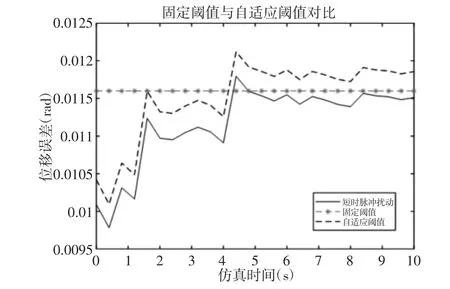
图12 无故障状态加入短时脉冲Fig.12 Adding aGlitch Without a Fault Condition

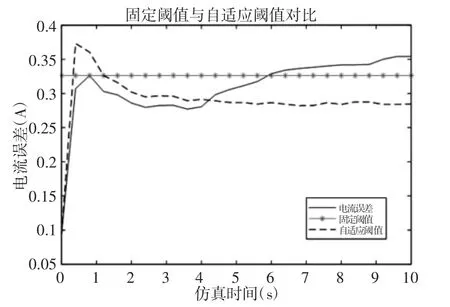
图13 电机绕阻故障Fig.13 Motor Winding Fault

4 总结

处理未知干扰和模型不确定性的影响是实际故障检测算法中一个重要的考虑因素。设计了一种将基于线性模型的方法与自适应阈值相结合的检测方案，用于检测非线性机电作动系统中的故障。理论和试验表明，机电作动系统是一个非线性系统，把其线性化会对故障检测残差的设计造成很大的干扰。因此，基于未知输入观测器对系统干扰和建模不确定性进行解耦，减小了不确定因素对残差的影响，降低了故障检测误报警率。并通过使用自适应阈值来考虑模型建模误差以及干扰和噪声引起的不确定性，能够在故障早期有效的检测故障。并基于Simulink 建立了三闭环机电作动系统动力学模型，验证了算法的有效性。所提出的方案已被证明能够检测机电作动系统其它不同类型的故障。

但是，由于飞控机电作动系统是一种非线性、多变量、强耦合的系统，对于滚珠丝杠等机械结构，摩擦和间隙等非线性因素对系统影响较大，建模往往并不能真正反映实际系统。因此后期应基于机电作动系统试验平台验证故障检测算法的有效性。