有限长周期性结构的水下声学性能分析

叶韩峰，陶 猛，李俊杰

（贵州大学机械工程学院，贵州 贵阳 550025）

1 引言

局域共振声学超材料是在声子晶体研究中发现的新型人工周期材料[1]。周期性局域共振结构能够以远小于波长的小尺度结构形式阻隔特定频率范围内的波传播，所以在减振降噪领域具有广泛的应用价值和前景。目前对于周期性局域共振结构的研究方法主要有：传递矩阵法、平面波展开法、集中质量法、统计能量法、有限元法、谱有限元法和波导有限元法等。国内外对于周期性局域共振结构也有诸多研究。文献[2]利用传递矩阵法求解了层状周期性结构的带隙问题，并用有限元软件ANSYS 对层状周期性隔振墙进行了频率响应分析。文献[3]利用导纳法和传递矩阵法，研究了半无限长和有限长周期结构在纵向力、横向力和弯矩作用下对于带隙结构的影响。文献[4]提出了一种具有负泊松比的周期性蜂窝结构，利用有限元法分析了其动态压缩性能。文献[5]利用平面波展开法（PWE）研究了周期性局域共振结构的材料组分、点阵结构、散射体形状和填充率对于带隙的影响。文献[6]结合超声浸水透射技术，测试了单胞包含6 晶格钢/水声子晶体在第一布里渊区的带隙性质，并与基于有限元法的结果进行了对比验证。文献[7]利用波有限元法（WFE）研究了有限长周期性结构在局部扰动作用下的动态响应。文献[8]利用有限元法对添加了多层橡胶基体与振子的局域共振单元对于低频带隙和带隙拓宽的影响。文献[9]对基于西尔宾斯基三角（Sierpinski Trangle）排布的多孔周期性结构的带隙特征进行了分析。

目前对于周期性局域共振结构的研究大多是以无限大周期结构为研究对象，主要探讨单元材料结构参数变化对于其带隙的影响，其带隙特性一般只是对在某几个较小频率范围内的声波完全阻隔。在实际应用中，一方面不可能制造出无限大结构，另一方面也需要关注结构在整个频率段的吸声隔声性能。而目前有关于有限长周期性局域共振结构声学性能的研究并不多。因此，基于有限元COMSOL 软件，分析了有限长度情况下二维三组元的局域共振结构的声学性能。

2 理论与验证

2.1 基于有限元方法的频散曲线计算

根据弹性力学理论，在无初始应力的自然状态下，理想弹性介质的变形是微小的，弹性波在均匀、连续、完全弹性介质中传播时，质点的运动方程[10]为：

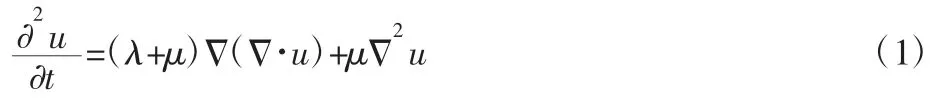
式中：ρ—介质密度；u—质点位移，在二维模型中，u=［ux，uy］；λ、μ—拉梅常数

在周期场中，根据Bloch 理论，波动方程的解u（r，t）满足下式[2]：

在划分完网格后，模型可以转化成普通的弹性特征值问题，特征值线性方程[11]，如式（3）所示。

式中：K—整个系统的刚度矩阵；M—系统的质量矩阵。

由式（2）可知，k 在上叠加一个倒格矢G，结果不变，即不同的波矢k 对应于相同的本证函数，所有周期性结构的本征模式具有一定的对称性。因此，Bloch 波矢一般选择其中模值最小的单元，它们所组成的集合称为第一布里渊区。

最后在后处理过程中，只需要扫描第一布里渊区内的波矢k，即可以得到以波矢为横坐标，本征频率为纵坐标的频散曲线（也称频率带隙图）。

2.2 模型的验证

验证模型所用的验证单元，如图1 所示。验证单元为二维单元，其中由二个组元构成。组元1 为硅橡胶，其单元边长H0=0.02m；组元2 为铅，半径r=0.008m。具体的材料参数如下：硅橡胶的密度ρ1=1300kg/m3，拉梅常数λ1=6×105Pa，μ1=4×104Pa；铅的密度为ρ2=11600kg/m3，拉梅常数为λ2=4.23×1010Pa，μ2=1.49×1010Pa。

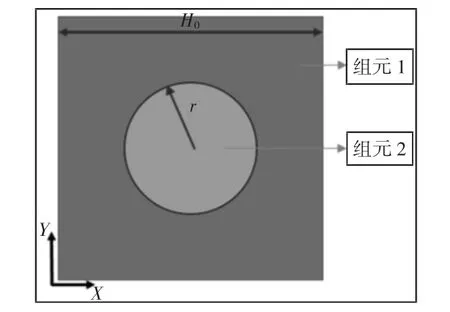
图1 二维二组元验证单元Fig.1 Periodic Unit of Validation Model

在软件中，通过把晶胞单元的四个外边分别设定成Floquet 周期性边界条件来仿真共振单元在X 和Y 方向上周期性排列，从而形成一个无限大结构。基于有限元法与文献[12]中基于集中质量法（LM）的带隙图对比，如图2 所示。需要指出的是，本验证模型计算了前8 阶特征频率的结果，而文献[12]中只计算了前6 阶的结果，因而在（600～800）Hz 基于FEM 的频散曲线多了两条。根据图2，不难看出，基于有限元法的带隙与集中质量法的带隙的整体变化趋势一致，两者之间仅仅存在较小的误差，最大误差值小于50Hz。因此，可以证明基于有限元法的局域共振单元带隙图是正确的。

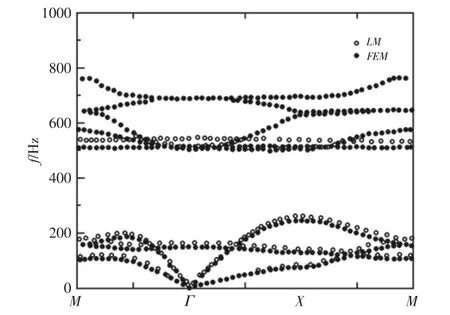
图2 集中质量法与有限元法的带隙图对比Fig.2 Comparison of Band Gaps Based on LM and FEM

3 声学性能分析

以二维三组元周期性局域共振单元为研究对象，如图3 所示。前8 阶特征频率的带隙图，如图4 所示。图3 中，组元1（基体）为硅橡胶，外径r1=0.006m，组元2（振子）为铅，半径r2=0.004m，组元3（包裹层）为环氧树脂，边长H=0.014m。组元3 环氧树脂的密度ρ3=1180kg/m3，拉梅常数λ3=4.43×109Pa，μ3=1.59×109Pa，硅橡胶与铅的材料参数同上节。

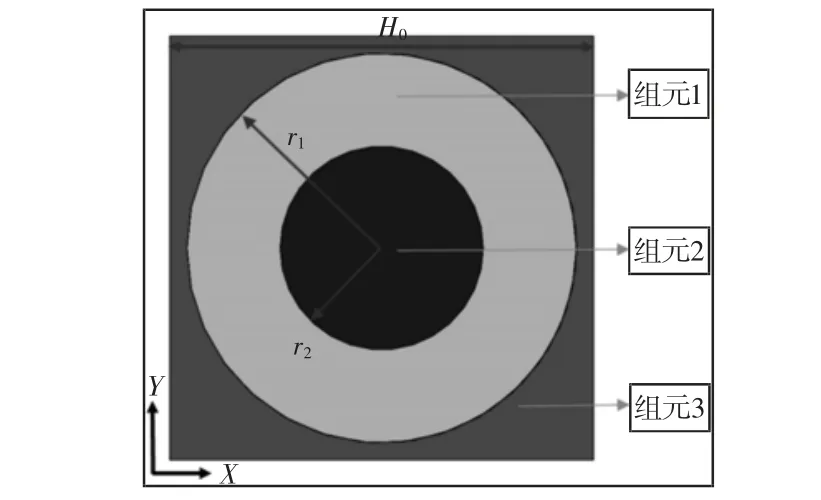
图3 仿真模型的周期性单元Fig.3 Periodic Unit of Simulation Model

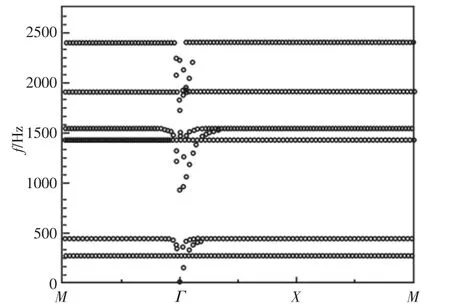
图4 二维三组元局域共振单元带隙图Fig.4 Band Gap of Simulation Model

根据图4，当频率低于2500Hz 时，该结构有两条带隙，其频率范围分别为（400～900）Hz 和（1500～1700）Hz，即表示对于（400～900）Hz 和（1500～1700）Hz 范围内的声波无法在该结构中传播。但是由于在实际应用中不可能制造出无限大结构，无限大周期结构的带隙只是一个理想的理论值，而关于有限大结构的声学性能如何才是研究的重点。

基于图3 中的二维三组元局域共振单元，建立了10 晶胞有限周期局域共振结构的仿真模型，如图5 所示。模型从左至右依次为，完美匹配层（PML）、介质1、有限长共振结构、介质2 和完美匹配层，其中介质1 和2 均为水介质，厚度为80mm；而完美匹配层的厚度为50mm。声波从介质1 垂直入射到局域共振结构，在交界面处反射回介质1 的声波会进入左侧PML 之中，从而避免声波的二次反射；同样地，从局域共振结构透射进入到介质2 中的声波会进入右侧PML，不会再重新回到局域共振结构之中。介质1 与局域共振结构的交界面以及介质2 与局域共振结构的交界面均被设定为流固耦合面。入射平面波是通过在介质1 中设定背景压力场来实现。

图5 10 个单元组成的局域共振结构Fig.5 Finite Length Periodic Structure Composed of 10 Units

3.1 十晶胞厚局域共振结构的声学性能

在平面波垂直入射条件下，10 个晶胞厚局域共振结构的声学性能，如图6 所示。单个晶胞的材料与结构参数同上节。10 个晶胞厚局域共振结构在500Hz 和1600Hz 处的反射系数都高达0.85 以上，其中在1600Hz 处的反射系数接近1，而透射系数和吸声系数都低于0.1。500Hz 和1600Hz 分别处于图4 所示无限大周期性结构的两条带隙频率范围（（400～900）Hz 和（1500～1700）Hz）之中。因此，对于带隙频率范围内的平面波，无限大结构可以完全阻隔其传播，而对于有限长局域共振结构而言，虽然不能完全阻隔声波的传播，但是仍能反射绝大部分声能量。

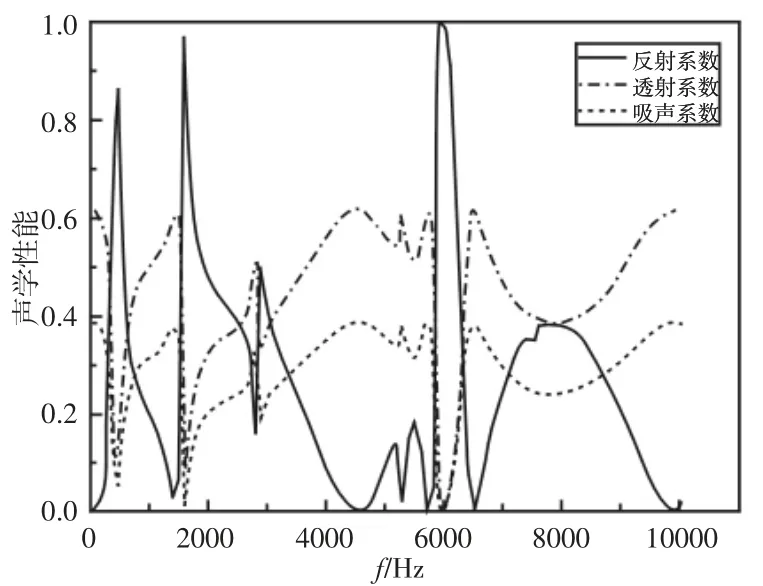
图6 10 个晶胞厚结构的声学性能Fig.6 Acoustic Performance of Finite Length Periodic Structure Composed of 10 Units

3.2 晶胞个数的影响

将图5 中周期性单元的个数分别变成5，10 和20，其他材料与结构参数保持不变，晶胞个数（厚度）对于有限大局域共振结构声学性能的影响，如图7 所示。随着晶胞个数的增加，带隙频率处的反射系数显著增大，如在500Hz 处，晶胞个数为20 时反射系数接近于1，比晶胞个数为5 时的反射系数增大了一倍；另外，晶胞个数为20 时，（500～600）Hz 频率范围内的反射系数均高于0.8，而晶胞个数为10 时，只有500Hz 处的反射系数高于0.8，即随着晶胞个数的增加反射系数峰值范围得到拓宽，但是拓宽后的频率范围仍然处于图4 中第一带隙频率范围（400～900）Hz 之中。所以随着晶胞个数不断增加，有限大局域共振结构反射系数峰值范围会越来越接近无限大周期结构带隙频率范围。

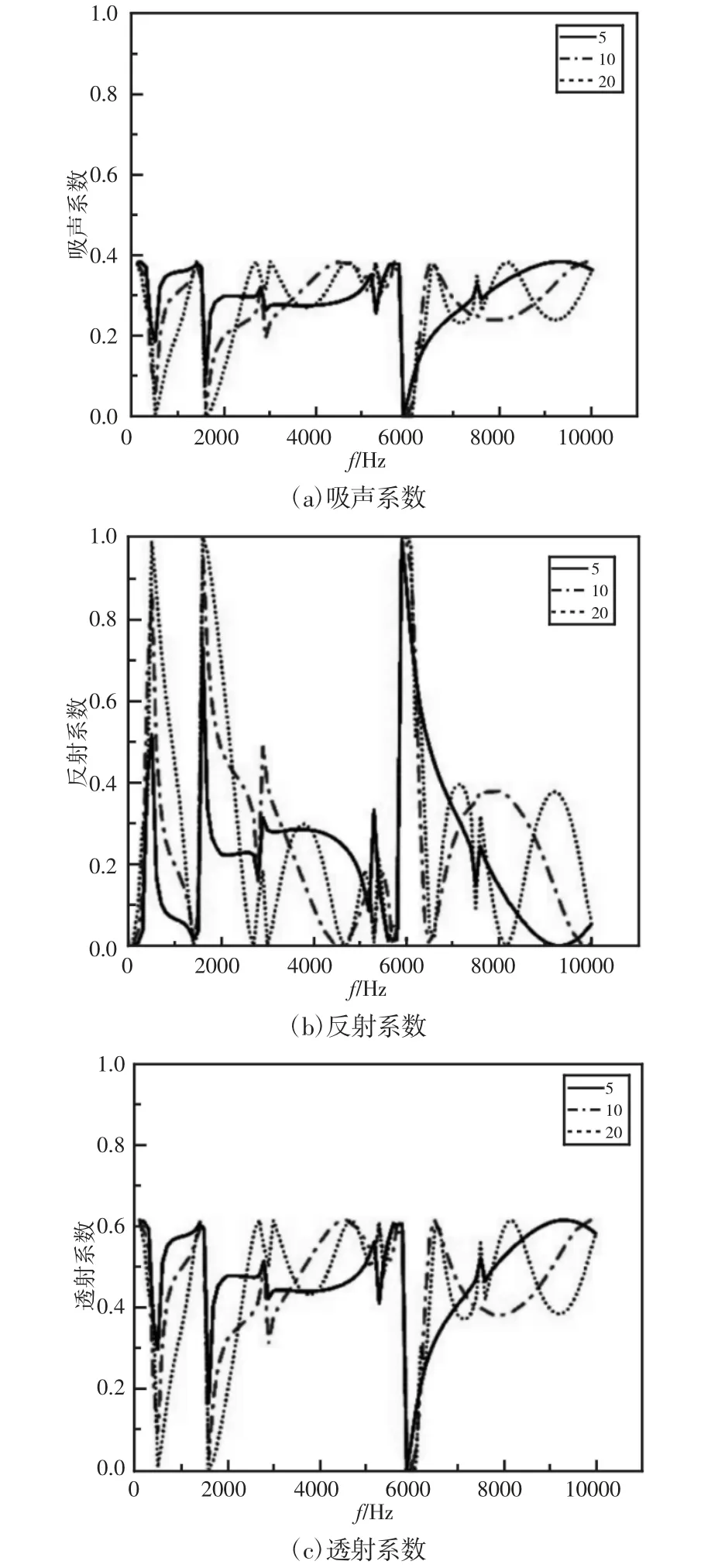
图7 晶胞个数对于结构声学性能的影响Fig.7 The Effect of Length on the Acoustic Performance

3.3 基体损耗因子的影响

周期性局域共振结构是利用软的基体（组元3）和包裹层（组元1）与硬的振子（组元2）的共振耗能来改善整个结构的声学性能。研究中基体材料多为橡胶材料，但是在之前的研究中很少考虑材料的损耗特性对于结构声学性能的影响。以图5 中模型为研究对象，其他参数不变，只考虑基体材料的损耗因子η3变化对于整个结构声学性能的影响，如图8 所示。需要指出的是，实际损耗因子应为与频率有关的曲线，在本研究中分别取损耗因子为0、0.1、0.3 和0.5。

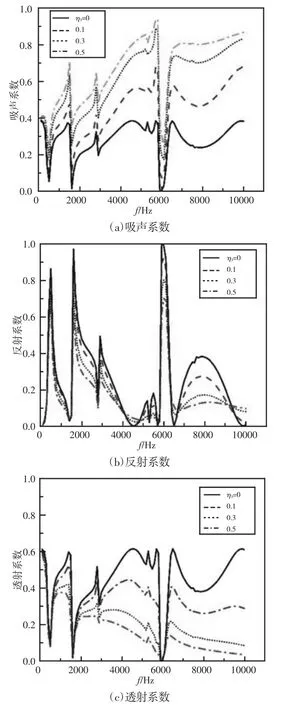
图8 基体损耗因子对声学性能的影响Fig.8 The Effect of Component 3’s Loss Factor on Acoustic Performance

在改变了基体材料的损耗因子后，整个结构的反射系数整体变化幅度不大，只有在高频处（7000～9000）Hz 有相对较大的减小，但是从吸声系数曲线可以看出，这种变化是因为在此频率范围内的平面波入射到结构之中后被损耗了所导致的；另外，由于整个结构的吸声性能在整个频率范围内都有较大的提升，所以透射系数也随着损耗因子的增大在整个频率范围都有较大的减小。根据吸声系数曲线和透射系数曲线，基体损耗因子的变化对于中高频段平面波的影响也明显高于低频段平面波。当基体材料的损耗因子达到0.3 后，虽然随着损耗因子继续增大仍能在一定程度上小幅度地提升结构的吸声性能，但是吸声性能的变化幅度明显小于当损耗因子从0 增加到0.3 时。

3.4 空腔存在的影响

研究表明当周期性单元中出现缺陷时，会使结构的带隙特征出现变化[13]。以图5 所示10 晶胞局域共振结构为研究对象，将从声波入射端起的第5 个晶胞的振子单元由铅核替换成空气从而形成空腔缺陷。以基体损耗因子η3为0 和0.5 的10 晶胞厚局域共振结构为研究对象，其他材料与结构参数保持不变，分别对比了第5 个晶胞在有无空腔存在时的声学性能，如图9 所示。由于空腔的存在，（2000～2900）Hz 范围内的吸声性能得到一定的提高，但是在（3000～4000）Hz 范围的由于反射系数变大，进入结构的声能量减少，吸声系数反而稍稍降低；另外，由于空腔的存在，在（8500～8700）Hz 范围内的平面波被大部分反射，如在8700Hz 处第5 晶胞为核空腔损耗因子为0 的结构反射系数接近1，依照反射系数峰值频率与周期性共振单元带隙频率的对应关系，可以推断出，当第5晶胞振子由铅核替换成空腔缺陷时，在（8500～8700）Hz 范围内出现了一个新的带隙。以图5 所示10 晶胞局域共振结构为研究对象，在8700 Hz 处，当基体损耗因子为0 时，第5 晶胞核分别为铅核与空腔时的振型图，如图10 所示。根据图10，有空腔存在的结构在空腔处的位移幅度与无空腔结构相差1 个数量级。从图10（a）和图10（b）不难看出，两种结构呈现完全不同的振型。对于有空腔的结构，其共振主要集中在空腔附近，呈现放射状；而无空腔结构的共振主要集中在第3，4，5，9，10 晶胞处，并且各处晶胞结构位移幅值相差并不大。因此，空腔结构的出现改变了原有结构的共振特性，从而影响了结构的声学性能。

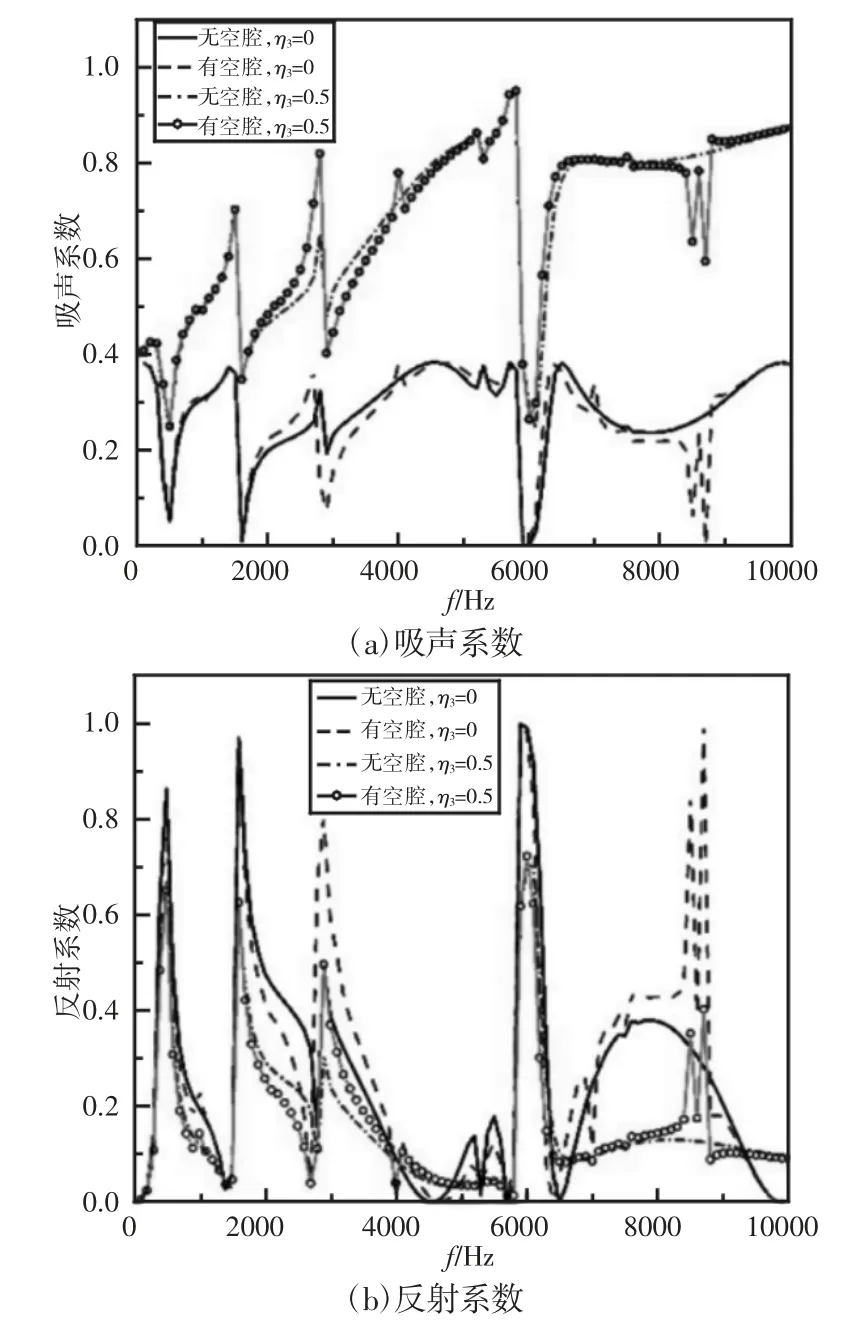
图9 有无空腔对吸声性能的影响Fig.9 The Effect of Hole’s Existence on Acoustic Performance

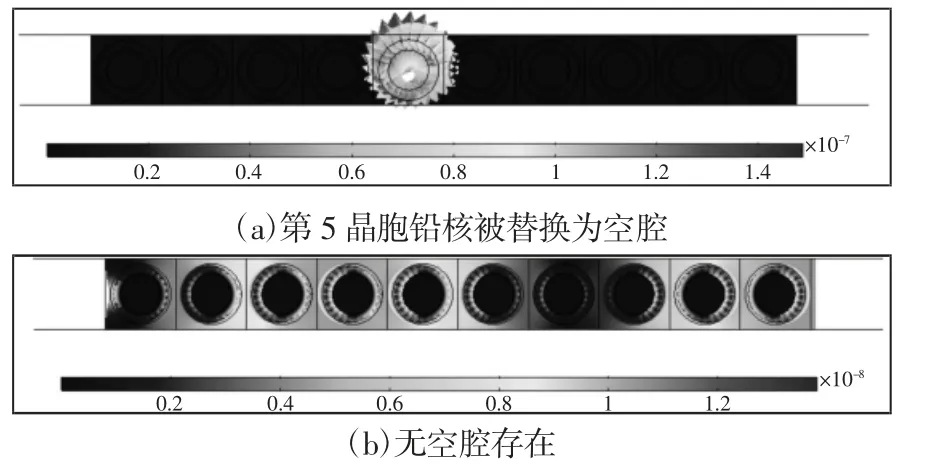
图10 结构振型图/mm，f=8700 Hz：Fig.10 Structural Vibration Pattern/mm，f=8700Hz

3.5 基体和包裹层损耗因子共同影响

以图5 所示的模型为研究对象，其他参数不变，只考虑基体（组元3）材料损耗因子η3和包裹层（组元1）材料损耗因子η1变化对于结构声学性能的影响，结果，如图11 所示。

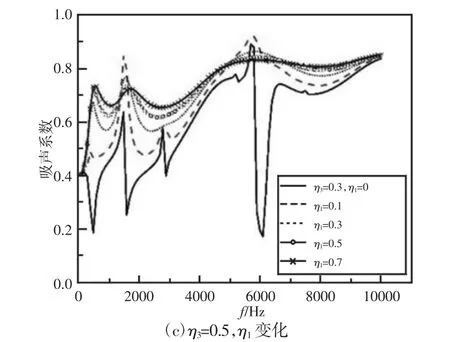
图11 组元1 和3 损耗因子对吸声性能的共同影响Fig.11 Co-Effects of Loss Factors of Components 1 and 3 on Sound Absorption Performance

整体上而言，两种材料的损耗因子越大，结构的吸声性能越好。根据图11（c），当基体损耗因子η3=0.5 时，包裹层损耗因子η1=0.7 时，结构吸声性能最好，吸声系数平均在0.7 以上。当包裹层的损耗因子为0 时，在6000Hz 处总会有一个吸声谷值，这是由于600Hz 处于带隙频率范围，入射的平面波大部份被反射了，而包裹层材料有损耗特性时，这个吸声谷值却没了，整个吸声曲线变得相对平滑，这表明包裹层材料属性的改变直接改变了结构的带隙特性。

4 结论

分析了在有限厚度情况下二维三组元的局域共振结构的水下声学性能。通过与已有文献的对比，验证了利用COMSOL 软件可以求准确计算局域共振结构的带隙曲线。基于该模型，分析了有限厚度的二维三组元局域共振结构，结果表明：（1）对于带隙频率范围内的平面波，有限长局域共振结构虽然不能完全阻隔声波的传播，但是仍能隔离绝大部分声能量；（2）随着晶胞个数的增大时，有限长局域共振结构的反射系数峰值范围会越来越接近无限大周期结构带隙频率范围；（3）空腔结构的存在和损耗因子的变化会改变原有结构的共振特性，从而影响结构的声学性能。