车床液压自定心中心架的受力分析与计算

谢祖强，林宗忠

（1.福建船政交通职业学院机械工程系，福建 福州 350007；2.福州晟尊咨询服务有限公司，福建 福州 350007）

1 引言

高性能数控机床离不开高精度的滚珠丝杠、直线导轨等细长轴类滚动功能部件。细长轴类零件因长径比大、刚性差，加工质量不易控制。为了提高细长轴类零件的加工精度，一方面采用特殊加工工艺补偿加工变形，一方面采用辅助支撑装置提高零件刚度[1-2]。实践证明，液压自定心中心架具有定心精度高，重复定位精度高，夹持范围大，安装操作方便等优点，是细长轴类零件加工理想的辅助支撑装置[3]。长期以来，欧美厂商生产的液压自定心中心架，以优异的性能占领国际市场，国内对其使用也主要依赖进口，使用成本高，因此该装置亟待国产化。近年来，国内研究人员对自定心中心架的研究取得了一系列的成果，众多学者对中心架核心部件平移凸轮机构进行理论研究建立了凸轮机构廓线方程[4-6]，文献[7-9]分析了凸轮机构的受力，提出机构的设计方法，文献[10-11]对中心架的联动复位机构进行研究，文献[12-13]对凸轮廓型加工进行研究，提出凸轮廓型加工方法。因此，国内对自定心中心架的研究正不断深入，在此基础上，对中心架机构进行受力分析，建立中心架机构的力学模型，为中心架机构高质量设计及高效应用提供理论依据。

2 自定心中心架的工作原理

自定心中心架的工作原理，如图1 所示。液压油缸1 驱动平移凸轮4 左、右平动，实现工件的松开或夹紧；活塞2 与平移凸轮4、滚轮E8 刚性连接，凸轮廓面与摆杆6 上滚轮A5 接触，驱动摆杆6 绕轴O1旋转，摆杆上滚轮C、D 与滚轮E，形成3 点夹持机构夹持工件。夹持过程中，滚轮C、D、E 同步运动，使被夹持工件的轴心始终保持在O3位置，实现全程自定心。

图1 自定心中心架的工作原理Fig.1 Work Principle of Self-Centering Centre Rest

3 中心架的受力分析

3.1 中心架机构的参数定义

中心架机构的参数定义，如图2 所示。以平移凸轮的底边为x 轴，平移凸轮的对称中心线为y 轴，建立直角坐标系xoy。设摆杆摆臂O1D 的长度为L1，摆臂O1A 的长度为L2，O1D 与O1A 的夹角φ，摆杆旋轴中心点O1与工件轴心O3的距离L0，O2O1与O1O3的夹角为β，在任一夹持工况下O3O1与O1D 的夹角∠DO1O3为α，摆杆滚轮C、D、E 的半径为r，滚轮A、B 的半径r0，被夹持工件半径为R，∠O2O1A 记为δ=φ-α-β，滚子A 与凸轮接触点为H，AH 与水平方向的夹角为ψ，MA 垂直于AO1，∠MAH=θ，液压油缸活塞直径为d，活塞杆直径为d1，无杆腔的压力为p0，有杆腔的压力为p1。

图2 中心架机构参数定义图Fig.2 Parameter Definition of Centre Rest Mechanism

3.2 无切削力作用下受力

根据力系平衡原理，在不考虑切削力的条件下，分别对被夹持工件、摆杆、平移凸轮进行受力分析。

3.2.1 被夹持工件受力

被夹持工件受三个滚子C、D、E 的夹紧力作用下处于平衡状态，如图2 所示。FD与FC的夹角∠CO3D=180°-2（Ω-β），FD与FE的夹角∠EO3D=90°+Ω-β，FC与FE的夹角∠EO3C=∠EO3D，根据正弦定理可得：

因FC=FD，得：

3.2.2 平移凸轮受力

3.2.3 O1侧摆杆的受力分析

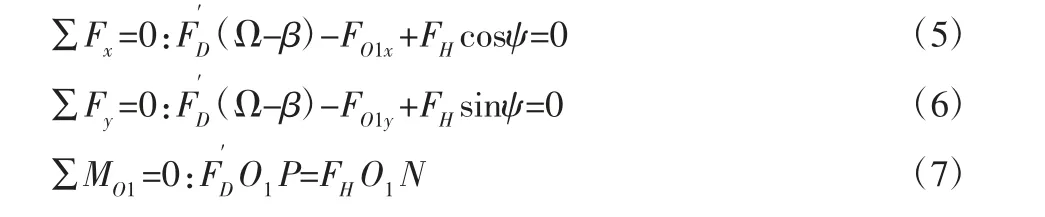
联立上述方程，解得：

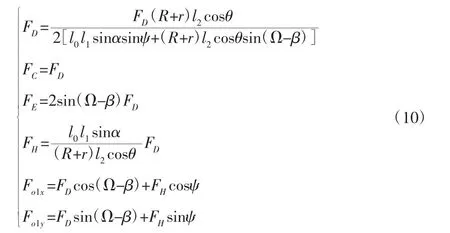
3.2.4 受力与油缸推力的关系

通常将自定心中心架三个滚子夹紧力的数量和称为中心架的夹紧力，考察中心架三个滚子夹紧力的数量和与液压油缸推力之间关系。式（10）中，令：

将式（11）代入式（13）整理得：

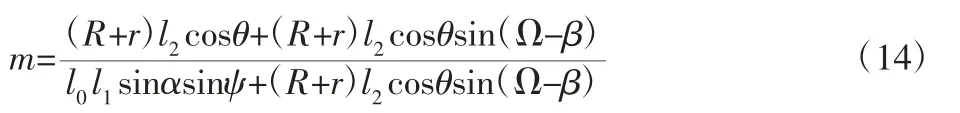
将ψ=θ+δ-90°代入l0l1sinαsinψ 得：

可得：m=1，则：FC+FD+FE=Fd，即自定心中心架三个滚子夹紧力的数量和等于液压油缸推力。故式（10）中：FD表达式可改写为：

同理可得：Fo1y=1/2Fd，即O1侧摆杆旋轴沿y 方向的支座反力始终等于油缸推力的一半，这与整体法分析得到的结论一致。因此式（10）可改写为式（18）简洁形式，当其他结构参数确定后，各点的反力只与油缸推力Fd与α 角有关。

3.3 受切削力作用下受力

切削过程中，刀具与工件之间的作用力F 称为切削力。由于F 的作用破坏了左右摆杆受力对称性，左右摆杆各点受力将产生差异，故平移凸轮应受到机架对其的作用力FS而保持平衡状态。以下利用力系平衡原理对中心架各构件进行受力分析。

3.3.1 被夹持工件受力

被夹持工件受力，如图3 所示。工件受三个滚子的夹紧力及切削力F 共同作用下处于平衡状态，切削力F 通过工件的轴心，且与水平方向的夹角为ε。规定ε 逆时针为正，顺时针为负，F沿x轴负方向时ε=0°。

图3 被夹持工件受力图Fig.3 Force Diagram of Clamped Workpiece

根据力系平衡方程可得：

3.3.2 平移凸轮受力

图4 平移凸轮受力图Fig.4 Force Diagram of Parallel Motion of Cam

根据力系平衡方程可得：

3.3.3 摆杆的受力

分别对O1、O2侧的摆杆进行受力分析，FO1、FO2分别为O1、O2处支座反力。根据力系平衡，可得：

上述十个方程总共有十个未知数，解得：

由式（30）得：FC+FD+FE=Fd，即受切削力作用下自定心中心架三个滚子夹紧力的数量和等于油缸推力。当F=0 时，则式（30）计算公式与式（18）同；当F≠0，时，FD=0 即力F 增大到使滚子D 的受力为零处于临界状态，外力F 在D 滚子侧。可得：

式（32）给出了临界状态下液压油缸推力与切削力的关系。

4 切削力的确定

4.1 指数公式数学模型

目前实际生产中，切削力的计算多采用经验公式。在车削加工中，切削力可以分解为3 个相互垂直的分力，即切削力Fc、背向力Fp和进给力Ff，其经验公式如下[14]：

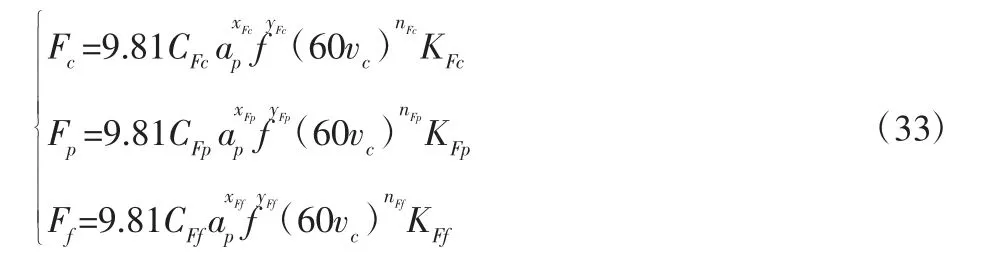
式中：CFx—工件材料和切削条件对三个分力的影响指数；xFx、yFx、nFx—背吃刀量ap、进给量f、切削速度vc对三个分力的影响指数；KFx—工件与刀具修正系数的乘积，KFx=KmFxKκrFxKγ0FxKλFxKκεFx。参数中的下标x 分别取c、p、f。由于进给力Ff施加在工件的轴向，在细长轴切削加工中对工件尺寸误差影响较小[15-16]，只考虑切削力Fc、背向力Fp的作用。故式（30）中的F=根据ε 定义

4.2 指数公式算例

为了分析自定心中心架的受力，选取一组切削参数计算切削力的大小。工件材料为45 钢调质，刀具材料为硬质合金YT15，刀具主偏角κγ=45°、前角γ0=45°、刃倾角λs=-5°、刀尖圆弧半径rε＝0.4mm，切削用量ap=2mm，f=0.16mm/r，vc=110m/min。查阅文献[17]可得式（33）中各参数值，计算得Fc＝523.23N，Fp＝191.55N，F＝557.20N，ε=-69.89°。

5 实例受力计算

自定心中心架的参数如文献[11]，如表1 所示。设计液压油缸直径d=50mm，油缸操作压力p=［0.6，5］，单位MPa。以夹持角α为变量，将上述数学模型，编写MATLAB 程序，分别得到无切削力作用及有切削力作用下中心架各机构的受力。

5.1 无切削力作用时受力计算

取液压油缸操作压力p=5MPa，油缸直径d=50mm，忽略油缸有杆腔的压力p0，则Fd=9817.477N，以夹持角α 为变量；令FZ=2FD+FE，ΔF0=FD-FE表示D、E 滚子夹紧力之差；FH可以分解垂直l2方向使摆杆转动的有用分力FHy=FHcosθ 和使摆杆压紧的有害分力FHh=FHsinθ，令η=FHy/FHh。由式（10）计算结果，如表1 所示。其中αop=29.320°对应FC、FD、FE两两之间的夹角为120°，表中F3、F4是根据文献[9]中式（5）计算得到，分别对应FE、FC。从表1 中可见：FZ=Fd，FO1y=1/21Fd；当α=29.320°时FC=FD=FE；FE、FD的计算结果与文献[9]中式（5）F3、F4的计算结果相等（精确到小数点后10 位），验证了公式的正确性。因此，简式（18）为无切削力作用时中心架各受力点系列受力计算公式，表达式简洁、完整，便于设计计算。

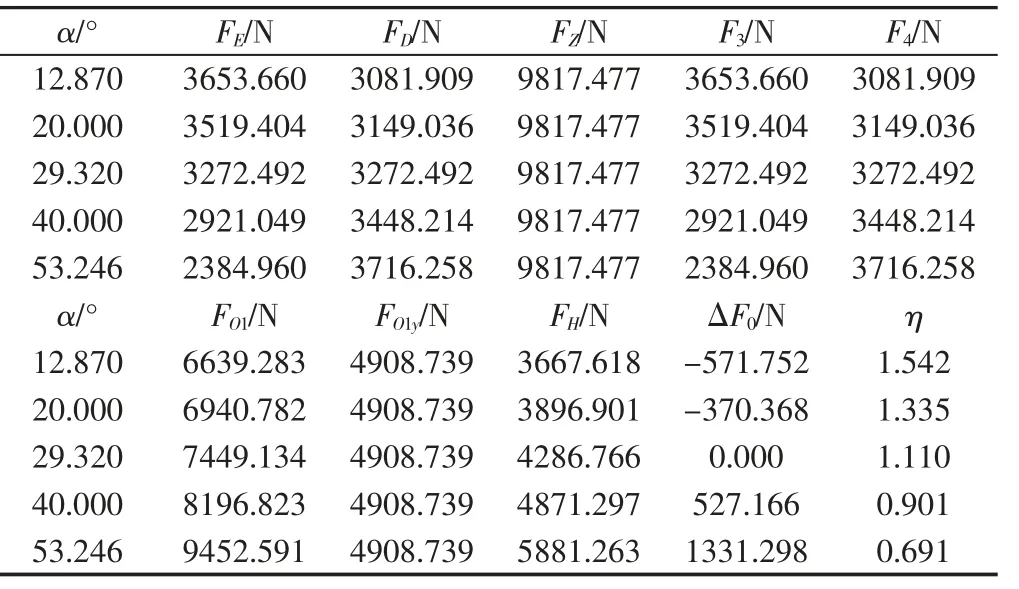
表1 无切削力作用下力计算值Tab.1 Force Calculated Value without Cutting Force

从表1 中可见，随着夹持角的增大，虽然三个滚子夹紧力的数量和总等于油缸推力，但是三个滚子夹紧力是单独变化的，其中FD值随之增大，FE值减小，同时FO1、FH值增大，ΔF 值随之增大且当α<αop时FDαop时FD>FE，但先减小直到α=αop时后再增大，FH有用分力与有害分力的比值η 不断减小。因此，随着夹持角的增大，中心架O1、O2支点以及平移凸轮、摆杆受力工况都是不断恶化，当工作在最大夹持半径时，中心架处于最差受力工况。对于夹持工件，当夹持角α=αop时，中心架处于最稳定夹持工况，故中心架夹持工件半径应在最佳夹持工况附近。最佳夹持工件半径为：

5.2 切削力作用时受力计算

当作用在被夹持工件上的力：F=557.20N，ε=-69.89°时，液压油缸推力与无切削力作用时同。由式（30）、式（31）计算结果，如表2 所示。表2 中，FC、FD、FE的计算结果与文献[9]式（9）F4、F5、F3结果相等（精确到小数点后10 位），验证了公式的正确性。因此，式（30）、式（31）为切削力作用时中心架各受力点系列受力计算公式，表达式简洁、完整。（注：文献[9]式（9）F4的表达式第一项分母Fd前少一个“负”号。）

表2 切削力作用下力计算值Tab.2 Force Calculated Value with Cutting Force

从表2 中可以看出，在切削力作用下，随着夹持角的增大，三个滚子夹紧力的数量和等于油缸推力。各支点的受力变化趋势与无切削力作用下相同。当α 角相同时，除了切削力作用侧的滚子的受力FD外，其余各点的反力在均比无切削力作用时大。当α角最大时，中心架处于最差受力工况。

在切削力作用下，令ΔF1=FC-FE，ΔF2=FD-FE，ΔF3=FC-FD。由式（30）可见，ΔF1、ΔF2与参数α、Fd、F、ε 有关，ΔF3与参数α、F、ε 有关。当其他参数不变时，ΔF 与α 角的关系，如图5 所示。由图5 可见，ΔF1、ΔF2的变化趋势与ΔF0相同，但数值比ΔF0大，而ΔF3的变化趋势平缓且数值较小，而最佳夹持角α 略小于αop。当α 不变时，ΔF1变化值与Fd、F、ε 中其中2 个参数的双因数变化，如图6～图8 所示。图中压力p 对应Fd。由图可见，ε 对ΔF1的影响显著，ε 从-90°到90°变化过程使ΔF1显著减小。当α=53.246°时，ΔF 与ε 角的关系，如图9 所示。由图可见，当ε=90°时，即切削力F 的方向沿着中心架中心并指向滚子E 时，ΔF 最小，故当切削力确定后，可以通过调整中心架与车刀的相对位置获得良好的夹持性能。如在卧式车床上，中心架可采用卧式安装方式，获得良好的夹持性能。

图5 夹持角α 与ΔF 关系图Fig.5 Diagram of Relationship Between α and ΔF

图6 ΔF1 与（ε，F）关系图Fig.6 Diagram of ΔF1 Relationship Between ε and F

图7 ΔF1 与（ε，p）关系图Fig.7 Diagram of ΔF1 Relationship Between ε and p

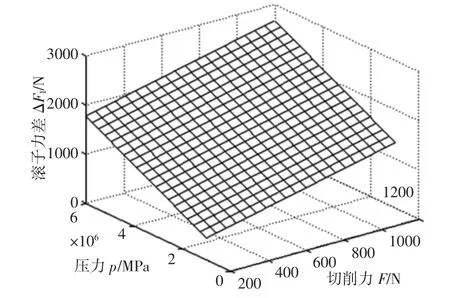
图8 ΔF1 与（F，p）关系图Fig.8 Diagram of ΔF1 Relationship Between F and p

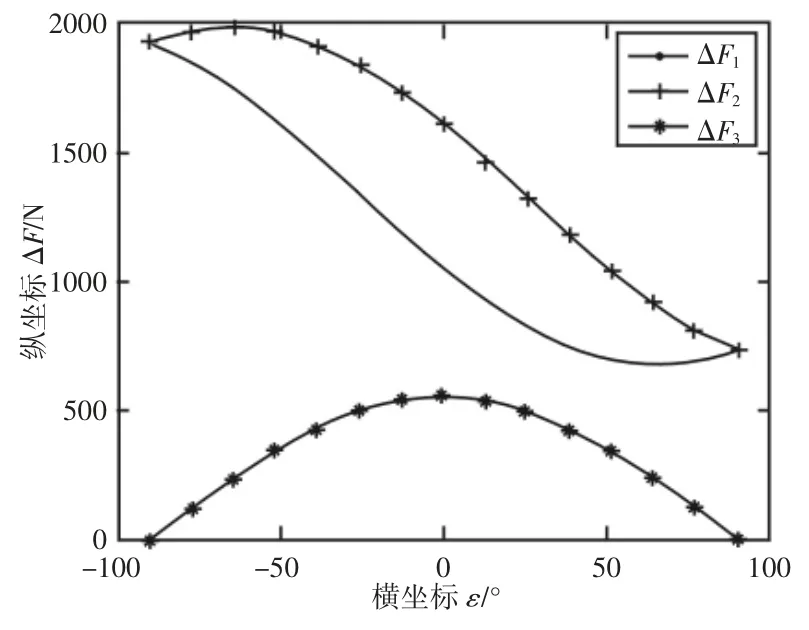
图9 ΔF 与ε 关系图Fig.9 Diagram of Relationship Between ΔF and ε

6 结语

分析了自定心中心架的工作原理，运用工程力学的方法对机构受力进行分析，建立中心架机构受力计算数学模型，为中心架机构的高质量设计及高效应用提供理论依据。结论如下：

（1）以细长轴外圆车削为例，建立了被夹持工件在无切削力和有切削力作用下的两种力学模型，得到中心架受力计算系列公式，在MATLAB 中编程计算，与文献[9]中的公式比较，两种方法计算结果相等，验证了推出公式的正确性。表达式简洁、完整，便于自定心中心架的设计计算。

（2）在无切削力和有切削力作用下，任一夹持工况，中心架3个滚子夹紧力的数量和都等于液压油缸的推力。但随着夹持角的变化，每个滚子的夹持力是单独变化的。

（3）在无切削力作用时，随着夹持角的增大，中心架滚子E的受力减小，其余各点受力都增大，同时D、E 滚子的夹持力差ΔF0也不断增大；当α 最大时，中心架处于最恶劣受力工况；存在最佳夹持角αop使ΔF0=0，此时中心架处于最佳夹持工况。在有切削力作用时，各支点的受力变化趋势与无切削力作用下相同，但C、E 和D、E 滚子夹持力差值比ΔF0大，同时C、D 滚子夹持力差值变化平缓且数值较小，此时最佳夹持角α 略小于αop。

（4）根据推导的公式，定量地分析了参数Fd、F、ε 对ΔF1的影响，给出了双因素变化的三维曲面图，分析表明参数ε 对ΔF1影响显著。当ε＝90°时，ΔF 值最小，因此通过调整中心架与车刀的相对位置可以获得中心架良好的夹持性能。