基于Lyapunov 理论的线控转向系统稳定性分析

田军南，谭光兴，冯楚楚，段方宾

（广西科技大学电气与信息工程学院，广西 柳州 545006）

1 引言

控制系统最重要的特性是它的稳定性，一个不稳定的系统是无法完成预期控制任务的。线控转向（steer by wire，SBW）系统作为未来汽车转向发展的热点和必然趋势，其稳定性的研究尤为重要。因此，对SBW 系统动力学分析，得到其稳定性条件，从系统与控制理论角度揭示SBW 系统与汽车系统运动稳定性内在规律和相互联系十分必要。

目前在SBW 系统稳定性的研究中，主要采用设计控制器以及优化控制策略来保证系统稳定性。从理论上分析SBW 系统稳定性并研究其对整车操纵稳定性影响等方面的研究尚不多[1-2]。文献[3]通过设计了无源控制器，解决了受实际系统传感器精度及信号噪声等因素影响引起SBW 双向控制的失稳问题；文献[4]提出了一种利用LQG/LTR 理论来提高系统稳定性和抗干扰能力的控制策略，并对所提出的的控制策略进行了稳定性与可行性验证；文献[5]针对汽车SBW 系统的操作稳定性问题，设计了固定转向灵敏度的汽车横摆角速度与质心侧偏角控制策略，并基于dSPACE 的SBW 硬件在环仿真实验台架对控制策略进行了验证；文献[6]利用汽车操纵稳定性综合评价指标与遗传算法结合，在不同的车速下优化了横摆角速度增益值，仿真验证了通过优化变角传动提高汽车的操纵稳定性可行性。在前述研究的基础上，拟按照降阶建模的思想对SBW 系统进行合理简化建立模。随后用动力系统稳定性理论分析模型的动力学行为，研究SBW 系统动力学模型的零解的稳定性条件，并依此选取了一组系统的结构参数。最后，利用Carsim 构建SBW 系统整车模型，研究SBW 系统关键参数对整车操纵稳定性的影响。结果表明，SBW 系统对整车操纵稳定性影响明显。运用所研究成果可定量分析SBW 系统参数对汽车转向安全性和稳定性的影响，为后续研究SBW 系统控制策略奠定了良好的基础[7]。

2 SBW 系统动力学模型建立

2.1 SBW 系统组成

SBW 系统由转向执行总成、转向盘总成、主控制器（ECU）三大部分组成。系统还包括故障容错系统，电源系统，车载通讯网络等辅助系统[8]。其结构简图，如图1 所示。转向执行总成模块的主要功能是接收主控制器所发出的指令，通过齿轮齿条转向器产生齿条位移，从而实现驾驶员驾驶意图。同时将汽车的动态信息通过传感器转换成电信号传输到主控制器帮助驾驶员对汽车进行实时控制。转向盘总成主要功能是将作用在方向盘上的力矩信号经过传感器转换为电信号传递给主控制器，同时根据主控制反馈的电压电流信号产生相应力矩帮助驾驶员感知路面信息。主控制器的作用是协调控制转向系统的各个模块，完成转向过程。

图1 SBW 系统结构简图Fig.1 SBW System Structure Diagram

2.2 转向盘总成建模

以方向盘作为研究对象，考虑转向时方向盘产生阻尼、转动惯量以及转向柱所受到力矩。由牛顿运动定律受力分析，由此可得转向盘车辆动力学平衡方程[9]，如式（1）所示。

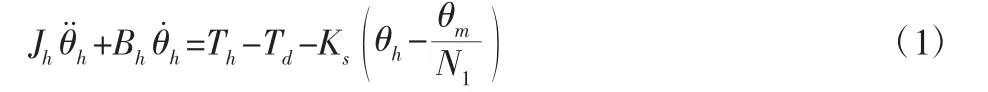
2.3 转向执行总成建模

为了方便研究，将转向执行总成简化为转向前轮组件与齿轮齿条组件。通过分析可得的齿轮齿条组件动力学平衡方程，如式2 所示。

Tp与TK的具体表达式，如式（3）所示。

且Xr、NL与θU三者存在如式（4）的关系：

对转向前轮组件受力分析可得其动力学平衡方程，如式（5）所示。

2.4 电机模型

一般线控系统包含路感模拟电机与转向执行电机。为了研究的方便将两种电机均视为直流电机，动力学平衡方程，如式（6）所示。

电机的电学平衡方程，如式（7）所示。

上文中相关参数的具体物理意义，如表1 所示。

表1 SBW 系统主要参数物理意义Tab.1 The Physical Meaning of the Main Parameters of the SBW System

3 SBW 系统动力学模型稳定性分析

对所建的SBW 系统进行分析，可知其不符合叠加定理为非线性系统。目前，Lyapunov 方法是分析非线性系统稳定性的最成熟的方法。根据SBW 系统动力学模型特点，采用Lyapunov 第二法对其稳定性进行分析。具体做法是构造一个正定的广义能量函数V（x），在根据该函数性质判断系统稳定性[10]。由于该方法不需要求解系统方程，因此特别适合用于难以求解的非线性系统。令：

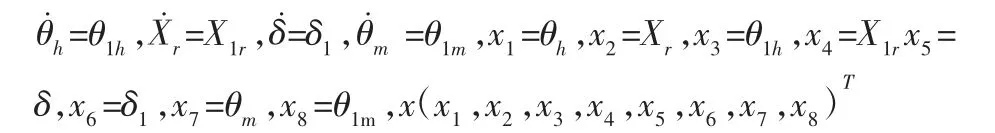
综合上述各模型，可以得到SBW 系统的微分方程组如下：

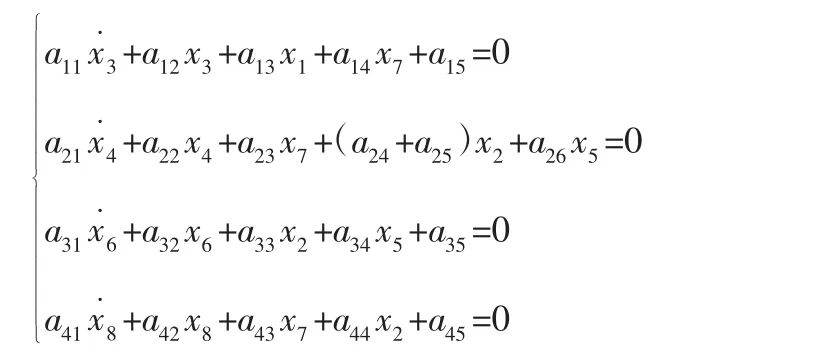
其中，各参数取值为：

忽略轮胎回正力矩与电机电磁力矩可得到SBW 系统的一个齐次微分方程组如下，还可得到该方程的一个平衡点为xe（0，0，0，0，0，0，0，0）。

根据Lyapunov 第二法选取正定的标量函数V（x），取值如下：

将函数V（x）在时间t 内导数可以得到：

其中矩阵A 可以表示为：

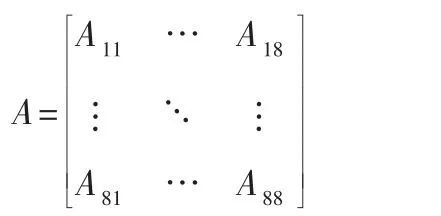
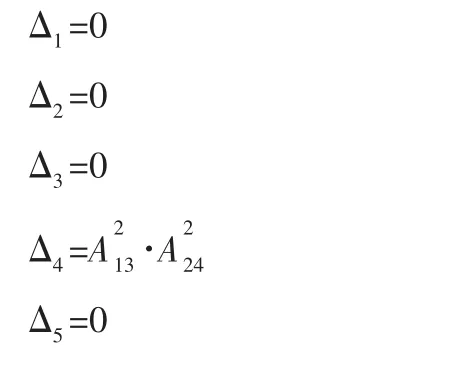
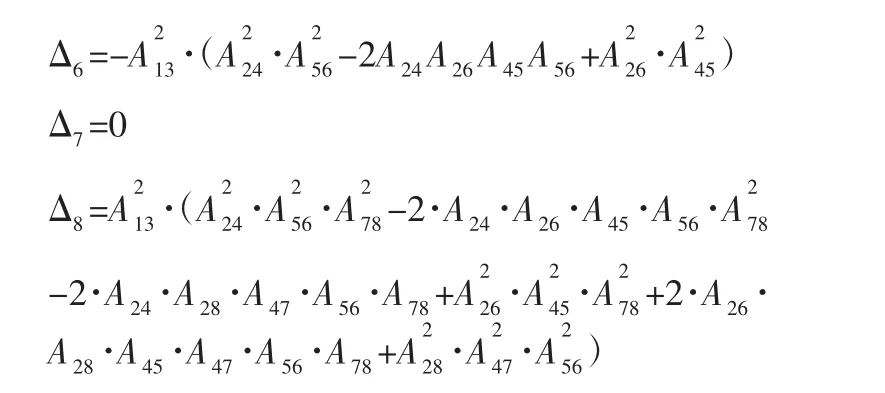
于是可以得到SBW 系统在平衡点xe稳定的条件为顺序主子式Δ4、Δ6、Δ8均不小于零。

依据上述SBW 系统的稳定性条件，进一步结合实际的结构参数选取条件，可取如下模型参数：

将数值代入SBW 系统的稳定性判定条件，可知其符合条件，系统稳定。

4 SBW 系统参数对整车系统稳定性影响

为了研究带有SBW 系统的车辆模型操作稳定性，选取SBW系统关键参数电机减速比、电机转动惯量为研究对象，利用汽车质心侧偏角与横摆角速度为整车稳定性评判标准。在SBW 系统稳定的条件下研究其参数变化对整车操纵稳定性影响。由于SBW 系统利用路感模拟电机代替传统机械装置产生路感，目前车辆安全法规不允许上路，而且当前SBW 试验车成本造价很高。因此采用仿真建模验证法验证SBW 系统对汽车操作稳定性影响。

4.1 基于CarSim/Simulink 联合仿真的线控转向汽车模型建立

为了尽量模拟实车模型采用汽车动力学仿真软件carsim 建立27 自由度车辆模型。取消CarSim 中的传统机械转向系统，将Simulink 构建的SBW 系统与CarSim 软件结合构建带有线控转向的整车模型。其中整车模型主要参数，如表2 所示。

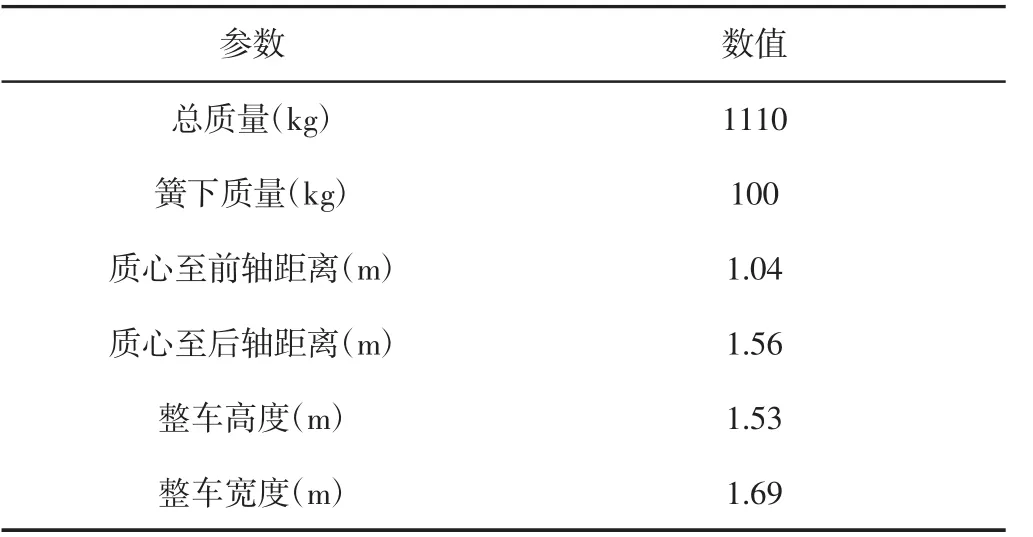
表2 整车模型主要参数Tab.2 Main Parameters of the Vehicle Model

4.2 电机减速比变化对汽车操作稳定性影响分析

在SBW 系统稳定的前提下固定其他参数令电机减速比N2分别取值10，20，30，用α 与β 分别表示汽车的横摆角速度与质心侧偏角。选取方向盘角阶跃试验工况进行仿真分析，仿真的车速取低速（30km/h）、中速（70km/h）、高速（130km/h）三个阶段。

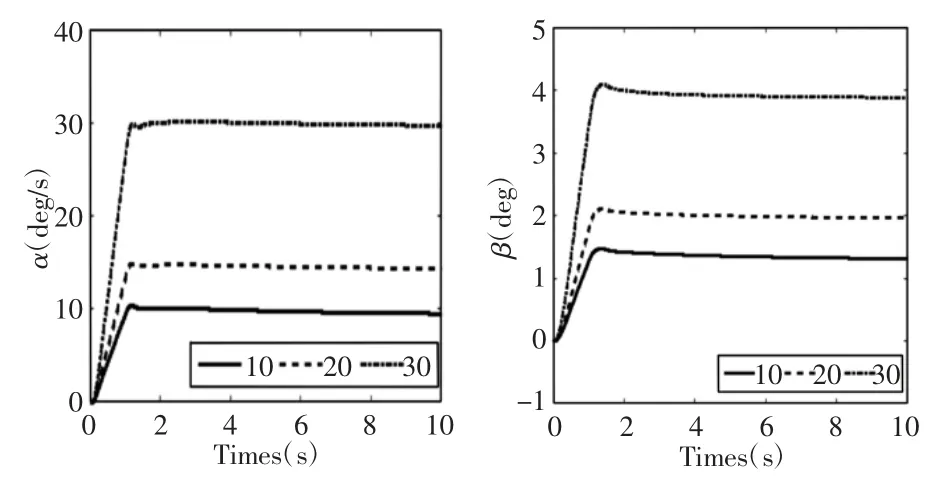
图2 低速行驶时汽车α 与β 瞬态响应曲线Fig.2 Transient Response Curve of Vehicle α and β at Low Speed

图3 中速行驶时汽车α 与β 瞬态响应曲线Fig.3 Transient Response Curve of Vehicle α and β at Medium Speed

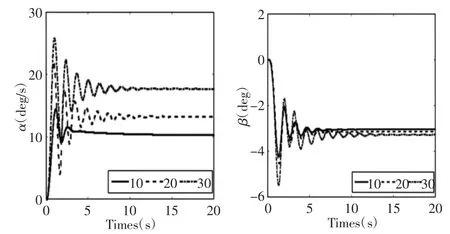
图4 高速行驶时汽车α 与β 瞬态响应曲线Fig.4 Transient Response Curve of Vehicle α and β at High Speed

表3 低速阶跃响应评价指标Tab.3 Low Speed Step Response Evaluation Index

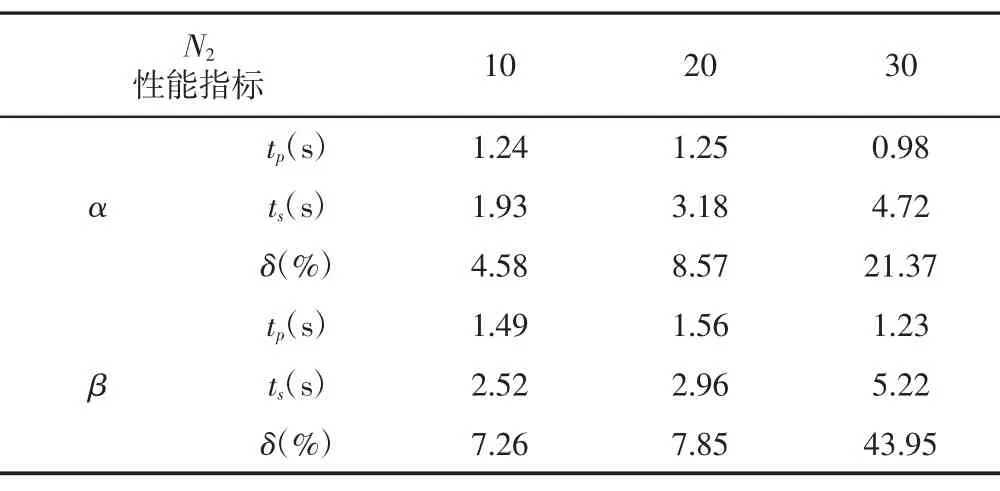
表4 中速阶跃响应评价指标Tab.4 Medium Speed Step Response Evaluation Index

表5 高速阶跃响应评价指标Tab.5 High Speed Step Response Evaluation Index

不同速度行驶时不同电机减速比的横摆角速度与质心侧偏角阶跃响应曲线，如图2～图4 所示。不同速度行驶时不同电机减速比横摆角速度与质心侧偏角瞬态响应指标，如表3～表5 所示。

观察图2 可以发现，汽车低速行驶下的横摆角速度与质心侧偏角的峰值与稳态值随着电机减速比的增加不断变大。从表3分析瞬态响应指标可以看出，随着电机减速比的不断增大使横摆角速度与质心侧偏角的上升时间tp，调节时间ts，超调量δ 不断增大。α 的上升时间从1.15s 延长到了1.21s，β 的上升时间从1.33s延长到了1.41s；α 的调节时间从1.39s 延长到了1.67s，β 的调节时间从1.81s 延长到了1.88s；α 的超调量从2.56%上升到了3.71%，β 的超调量从2.22%上升到了3.07%。可见低速行驶时随着电机减速比的增加系统响应变慢，阻尼程度与综合性能也逐渐变差，进而导致系统稳定性逐渐恶化。

观察图3 可以发现，汽车中速行驶下的横摆角速度与质心侧偏角的峰值与稳态值同样随着电机减速比的增加不断变大。从表4 分析瞬态响应指标可以看出，随着电机减速比的不断增大使横摆角速度与质心侧偏角的上升时间tp变化虽有波动但整体影响微弱，调节时间ts，超调量δ 则不断增大。α 的上升时间从1.24s减少到了0.98s，β 的上升时间从1.49s 减少到了1.23s；α 的调节时间从1.93s 延长到了4.72s，β 的调节时间从2.52s 延长到了5.22s；α 的超调量从4.58%上升到了21.37%，β 的超调量从7.26%上升到了43.95%。可见中速行驶时随着电机减速比的增加系统的响应略微加快，阻尼程度与综合性能则逐渐变差。同时相较于低速时调节时间与超调量的变化幅度显著增大。

观察图4 可以发现，汽车高速行驶下的横摆角速度与质心侧偏角的峰值与稳态值同样随着电机减速比的增加不断变大。从表5 分析瞬态响应指标可以看出，随着电机减速比的不断增大使横摆角速度与质心侧偏角的上升时间tp存在同中速时相同的波动，调节时间ts，超调量δ 则不断增大。α 的上升时间从1.14s 减少到了0.89s，β 的上升时间从1.27s 增加到了1.37s；α 的调节时间从3.24s 延长到了10.92s，β 的调节时间从6.47s 延长到了10.41s；α 的超调量从26.21%上升到了68.17%，β 的超调量从6.31%上升到了61.67%。可见高速行驶时随着电机减速比的增加系统的响应略微加快，阻尼程度与综合性能则逐渐变差。同时相较于中速时调节时间与超调量的变化幅度显著增大。

总的来说，忽略速度变化时上升时间的波动情况。可以看出不论是在高速、中速、低速下随着电机减速比的增加都会导致操作汽车的稳定性稳定性的恶化。故在转向执行电机设计时可在条件允许范围内适当减小其减速比。

4.3 电机转动惯量变化对汽车操作稳定性影响分析

在线控转向系统稳定的前提下固定其他参数令电机转动惯量Jm 的初始值为0.00087 分别取值1，5，10，15 倍。选取与上述研究电机减速比相同的工况与车速可得到不同速度行驶时不同电机转动惯量的横摆角速度与质心侧偏角阶跃响应曲线，如图5～图7 所示。不同速度行驶时不同电机转动惯量的横摆角速度与质心侧偏角瞬态响应指标，如表6～表8 所示。

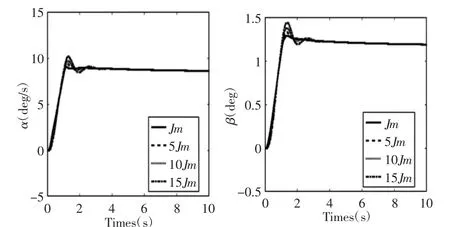
图5 低速行驶时汽车α 与β 瞬态响应曲线Fig.5 Transient Response Curve of Vehicle α and β at Low Speed

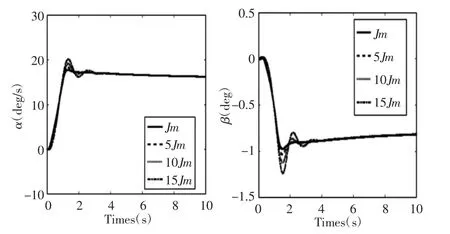
图6 中速行驶时汽车α 与β 瞬态响应曲线Fig.6 Transient Response Curve of Vehicle α and β at Medium Speed

图7 高速行驶时汽车α 与β 瞬态响应曲线Fig.7 Transient Response Curve of Vehicle α and β at High Speed

表6 低速阶跃响应评价指标Tab.6 Low Speed Step Response Evaluation Index

表7 中速阶跃响应评价指标Tab.7 Medium Speed Step Response Evaluation Index

表8 高速阶跃响应评价指标Tab.8 High Speed Step Response Evaluation Index

从图5 可以看出在低速时汽车横摆角速度、质心侧偏角的峰值随着电机转动惯量的增加不断变大，而稳态值几乎保持不变；从表6 中可以观察到，随着电机转动惯量的不断增大，汽车横摆角速度与质心侧偏角上升时间不断增大，这使得系统的响应速度逐渐变慢，但可以观察到其整体变化数值不大，影响微弱。同时可以观察到调节时间与超调量也不断变大，使得系统的阻尼程度与综合性能进一步增强。同时对中速以及高速分析，可以得到相同的结论。不同的是随着电机转动的不断增大其汽车汽车横摆角速度与质心侧偏角的操纵稳定性影响指标的数值进一步增大。

可以看出，不论是在高速、中速、低速下随着电机转动惯量的增加都会导致操作汽车的稳定性稳定性的恶化。故在转向执行电机设计时可在条件允许范围内适当减小电机的转动惯量。同时结合对电机减速比的分析，可以进一步警示我们在平常生活中应注意减速慢行这样可以更好的提高汽车行驶稳定性与乘车舒适性，避免交通事故的发生。

5 总结

运用Lyapunov 稳定性理论对SBW 系统模型的稳定性进行了分析，确定了SBW 系统的零解稳定性条件。在此基础上，通过结合Carsim 与matlab/simulink 构建了带有SBW 系统的整车模型，并分别在不行驶速度下研究了SBW 系统关键参数对整车操纵稳定性的影响进行了分析。结果表明，电机减速比与电机转动惯量对整车操纵稳定性影响明显。可通过适当减小电机减速比与减小转动惯量增强整车操纵稳定性。利用所研究成果可对SBW 系统的参数设计提供合理的依据，为SBW 系统控制策略的设计打下坚实基础。