混合w-facets成像并行算法研究

于昂，劳保强，王俊义，安涛

(1.桂林电子科技大学 信息与通信学院，桂林541004；2.中国科学院 上海天文台，上海200030)

1 引言

为了更深入地探索宇宙奥秘，射电望远镜朝着更高灵敏度、更高分辨率和更快巡天速度的方向发展。预计于2021年开建的平方公里阵(square kilometre array,SKA)射电望远镜，建成后将成为人类有史以来最大的综合孔径射电望远镜。该观测设备将为宇宙演化、引力的本质、生命起源、地外文明等重大前沿科学研究提供强有力的数据[1]。全数字化的SKA望远镜，规模巨大，将产生空前庞大的数据。SKA第一阶段(SKA1)每年将约有600 PB的数据产品传输到SKA区域中心，这些数据将有助于天文学家进行深度处理与分析[2]。最终用于发表的SKA数据产品需要经过无数次的反复处理与验证，因此SKA数据处理软件与算法的运行速度和有效性将大大影响天文学家的工作效率，甚至影响科学产出。

大视场成像是SKA1低频阵列(SKA1-low)数据处理的重要环节，如SKA1的首要科学任务宇宙黎明的探索，将利用SKA1-low进行宇宙再电离成像观测；SKA1十大科学目标之一宇宙磁场，也将利用SKA1-low进行大规模偏振成像观测。目前，应用比较广泛的大视场成像算法有faceting[3–5],w-projection[6],w-stacking[7],snapshots[8]和w-snapshot[9]。faceting和snapshots主要是利用数据分割技术，使得分割后的数据满足二维傅里叶变换近似成像方法。这种分割技术的成像方法由于需要循环处理多份分割数据，将消耗较多的计算时间和CPU资源。其中，faceting又分为图像域faceting和uv-faceting，图像域faceting需要对分割后的数据图像进行拼接，将会有图像边缘效应；snapshots最后也需要进行图像拼接，同样存在类似的问题。uv-faceting由于分割后的数据都在同一个网格上栅格化，经过二维逆傅里叶变换后将获得整个视场的图像，不存在边缘效应。

w-projection,w-stacking和w-snapshot这三种方法主要是通过修正w项来完成大视场成像，相比分割技术的方法，成像质量相对高一些。w-projection主要通过可见度数据与w核函数的卷积，将三维可见度数据投影到w=0平面，最后利用二维傅里叶变换进行成像。由于数据处理时，卷积核函数将存放在内存中，w-projection的卷积核是三维的w核函数，因此相比传统的二维卷积核将要消耗更多的内存。w-stacking可以说是w-projection的升级版，该算法在图像域进行w项校正，并使用多线程技术优化算法，减少了卷积核的内存使用，但是需要使用大量的内存存储w层的傅里叶变换数据。由于使用多线程加速，运行速度相比w-projection有很大的改善。w-stacking算法已经封装在wsclean软件中，主要用于SKA先导望远镜默奇森宽视场阵列(Murchison widefield array,MWA)[10]的数据处理。由于w核可以单独计算，并根据内存来选择任意w平面数，使得w-projection比较容易与其他算法进行结合使用。w-snapshot算法即是snapshots和w-projection结合的产物，结合后的算法改善了snapshots边缘的畸变问题，相比w-projection有更好的可拓展性。w-snapshot主要封装在ASKAPsoft软件中，用于SKA先导望远镜澳大利亚平方公里阵(Australian square kilometre array pathfinder,ASKAP)[11]的数据处理。

由于混合算法具备一定的优势，本文主要研究uv-faceting和w-projection的混合算法，助力SKA1科学数据处理。本文的混合算法，一方面，可以改善uv-faceting成像质量问题，包括噪声水平和动态范围等；另一方面，可以减少内存的使用，提高w-projection的可拓展性。为了提高该混合算法的运行速度，本文提出了两种并行优化方法：基于多核CPU的并行算法和基于GPU的并行算法。

2 混合w-facets成像算法

本文的混合成像算法，主要是将uv-faceting算法[4,5]和w-projection算法[12]结合以完成低频干涉阵列大视场成像，称之为混合w-facets成像算法，其中facets表示分面。该算法首先采用uv-faceting中的视场和数据分割技术获得分面数据；然后通过相位旋转技术获得每个分面的可见度数据，通过基线旋转技术获得每个分面的u和v坐标数据。其次，对每个分面的数据进行栅格化，栅格化的卷积核函数不再使用传统的卷积核函数，而是w-projection算法中的w核函数。每个分面的栅格化处理均在同一个网格中进行，因此栅格化后的数据进行逆傅里叶变换，只输出一个天空图像，即一个图像结果，也称为脏图。相比图像域faceting算法，本文的方法无需进行图像拼接，避免了图像拼接引起的图像边缘畸变，同时也减少了运行时间。此外，与w-projection结合后再与只使用uv-faceting相比，本文算法的成图质量和图像的动态范围将会进一步提高。

近年，Wortmann[13,14]提出的w-towers算法整体思想上与本文的w-facets算法类似，但具体设计思路不同。主要不同为：(1)w-towers的facets分割方法与图像域faceting方法相同，而w-facets是基于uvw域分割的。(2)w-facets方法中每个facet的数据在同一个大网格上进行栅格化，子网格实际上是按照facets数目进行严格均分而获得；而w-towers需要经过更复杂的计算，且每个子网格是由所有facets的数据构成的。(3)本文采用的是w-projection方法进行混合，w-towers采用的是w-stacking方法。下面详细介绍本文算法的公式推导过程。

在综合孔径成像原理中，经过射电干涉仪测量获得的可见度数据V(u,v,w)与天空亮度分布函数I(l,m)(即天空图像)存在如下关系[15]：

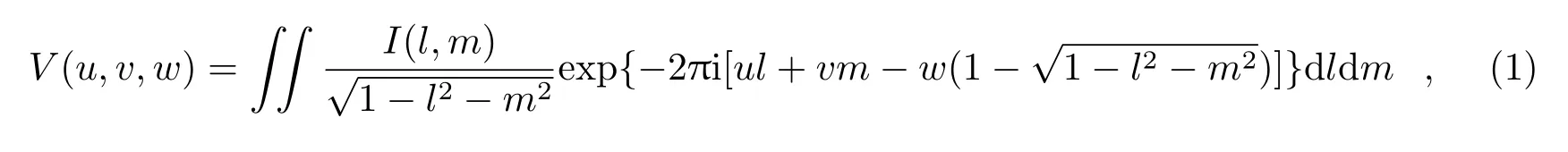
其中，u,v,w是射电望远镜的基线在u-v-w坐标系下的投影坐标，(l,m)为u轴和v轴观测方向上的单位向量的方向余弦，i是虚数单位。

为了使用二维傅里叶变换近似方法，可以将视场切割为Nfacets个相同大小的小视场(也称为分面)，当Nfacets满足下式条件，每个小视场将可以采用近似方法重建天空图像：

其中，Bmax是低频射电干涉阵列台站两两之间距离(基线)的最长值，max表示取最大值，λ是参考频率对应的波长，D是台站的直径范围。

每个小视场的可见度数据可以通过原始可见度数据进行相位旋转获得，令第j个分面的相位中心坐标为(lj,mj,nj)，则该分面的可见度数据Vj为[4,5]：

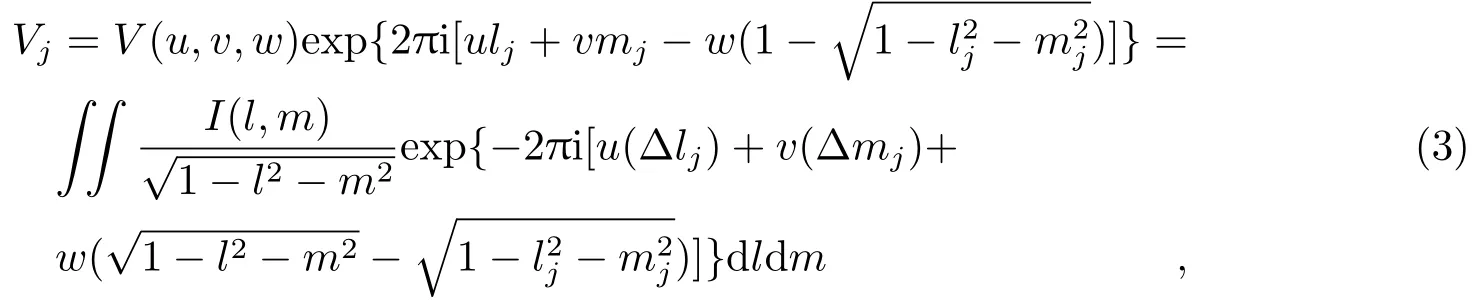
其中，Δlj=l-lj,Δmj=m-mj，(lj,mj,nj)可以利用分面相位中心的赤经RA和赤纬DEC，以及原始相位中心的RA和DEC，通过坐标转换公式计算出来[5]。

式(3)末尾的2个平方根项，经过泰勒一级近似展开，有：

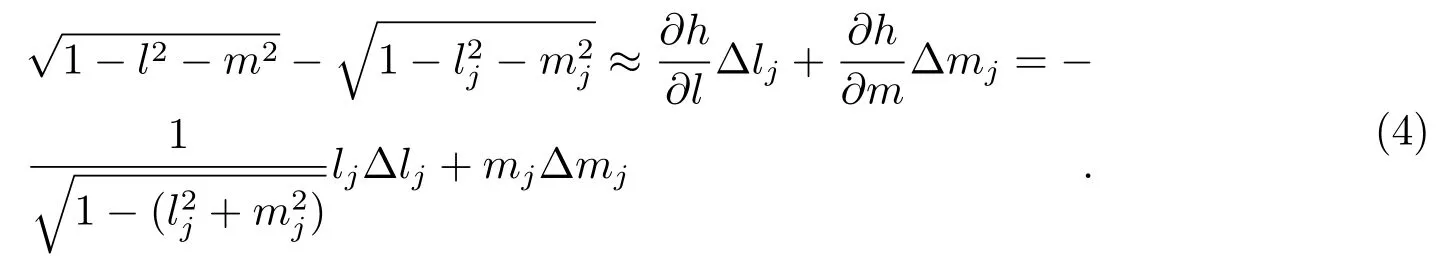
将式(4)代入式(3)后，得：

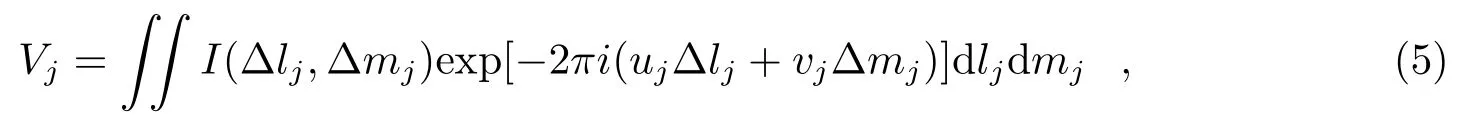
其中，uj和vj是第j个小视场的基线坐标，计算公式为：

随后，每个小视场的可见度数据和(uj,vj)数据在同一个网格上进行栅格化，再对整个网格数据进行二维逆傅里叶变换，即获得整个视场的脏图。其中，栅格化处理时，采用w-projection的w核函数与每个小视场的可见度数据进行卷积来完成。w核函数的表达式为[17]：

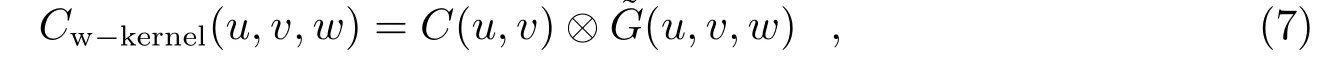
其中，C(u,v)是传统的卷积核函数，一般选取性能较优的球谐函数；表示卷积运算；(u,v,w)是G(l,m,w)的傅里叶变换，G(l,m,w)的表达式为[6]：

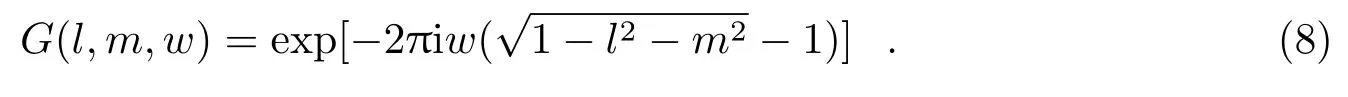
从w核函数的表达式可以看出，栅格化的卷积将多一个维度，也就是这个w核函数将由多个二维卷积核组成。值得注意的是，每个二维卷积核的大小不固定，将会随着w值和视场的增大而增大[6]。通常，在w=0时，二维卷积核的大小为7×7或者9×9[6]。由于一维卷积核函数是一种窗函数，所以一维卷积核函数的长度又称为全支撑大小。当w＞0时，全支撑大小可以由计算得到，其中Iwidth是脏图的最长边大小或完整图像的最长边大小，单位为rad。从上述分析可知，如果w平面数和图像过大则消耗的内存较多；w平面数取值过小，则将导致混叠效应产生。因此，w平面数取值应合理，我们给出每个分面较佳的平面数计算公式：

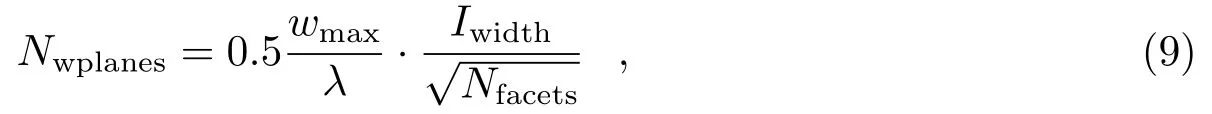
其中，wmax是w的最大取值。

uv-faceting与w-projection结合后，Nfacets在不满足公式(2)的情况下也能完成大视场成像，因为当Nfacets=1时，即进行w-projection成像。此外，Nwplanes与需要处理的图像大小会随着Nfacets的增加而减小，w核函数的最大全支撑大小也随之减小，因此本文的混合算法将大大减少卷积核内存的消耗。

Algorithm 1基于多核CPU的成像并行算法Input:V可见度数据，(u,v,w)基线坐标，Nwplanes w平面数，网格数组栅格存放栅格化结果全零数组(完整图像大小)Output:脏图1:#pragma omp parallel for schedule(static)2:for j in Nfacets do 3: for r in row count do 4: for c in channel count do 5: V,(u,v,w),RA0,DEC0=read data(r,c);6: RAj,DECj=calculate phase(RA0,DEC0,Nfacets)7: Vj=phase facets rotation(V,u,v,w,RAj,DECj);8: unew,vnew=baseline rotation(u,v,w);9: uscale,vscale=scale uv(unew,vnew);10:windex=w/wmax×(Nwplanes-1)11://w核栅格化12: for sv in 0 to cfullsupport[windex]do 13: for su in 0 to cfullsupport[windex]do 14:conv weight=Cw-kernal[windex][sv][su];15: grid[vscale+sv][uscale+su]+=Vj×conv weight;16: end for 17: end for 18: end for 19: end for 20:end for 21:dirty image=IFFT(grid)22:return dirtyimage

3 并行算法

3.1 基于多核CPU的成像并行算法

混合w-facets成像算法的数据处理过程与传统的射电干涉成像基本相同，大体包括4个部分：数据读取，卷积核函数的创建，栅格化和逆傅里叶变换。其中，栅格化至少包含5层循环处理过程，相对其他过程，需要消耗更多的运行时间。

因此，本文提出了一种粗粒度并行处理方法，实现每个分面数据的并行处理。采用开放式多处理(open multi-processing,OpenMP)并行技术，在最顶层加入并行任务调度，即可实现该循环的并行。本文主要采用静态调度方式，具体并行过程：当分配m个CPU核处理Nfacets个分面数据时，每个核(或线程)将处理Nfacets/m个分面的数据。当分配的CPU核数与Nfacets相等时，并行效果最佳。这种并行方法避免了并行化过程中可能出现的同步和锁的影响，是一种简单实用的并行方法。

基于多核CPU的混合w-facets成像并行算法的实现见Algorithm 1伪代码。算法的输入数据为校准后的数据，一般为宽带数据，有多个不同频率通道。最外的三层循环分别为：分面处理循环、按行处理循环和频率通道处理循环。内层的两个循环，主要完成栅格化处理；最外层，是根据CPU核数来进行分面处理的并行。最外三层循环，每一次将从输入数据中读取可见度、基线坐标u-v-w和原始相位中心RA0和DEC0等主要数据；接着，根据分面数目Nfacets和原始相位中心计算出当前分面的相位中心RAj和DECj。将公式(3)进行相位旋转，得到当前分面的可见度数据Vj；根据式(6)进行基线旋转，获得当前分面的基线坐标数据unew和vnew，并利用傅里叶变换缩放原理对旋转后的基线数据进行缩放。然后，通过w的最大值wmax和Nwplanes计算出当前w在w核函数的索引位置windex。

最后，通过二层循环完成栅格化，每次循环将通过windex获取w核函数的值，再与当前可见度数据进行乘累加。cfullsupport是w核中一维卷积核函数全支撑大小数组，通过windex获取当前w所需的全支撑大小。网格数组栅格的大小为完整图像的大小，经过逆傅里叶变换后将得到唯一脏图。

3.2 基于GPU的成像并行算法

GPU是一种可以一次并行运行数千个线程来实现快速计算的处理器，其计算能力是CPU的百倍。统一计算设备架构(compute unified device architecture,CUDA)的内部主要框架是以GPU中的线程块为组进行划分，每块由一个多核处理器控制，这意味着只需要控制多核处理器就可以同时控制和处理上万个线程。本文将利用CUDA编程实现基于GPU的混合w-facets成像并行方法。该方法主要将输入数据拷贝到GPU设备中,然后在GPU中进行并行的栅格化处理。该方法让主机负责整个系统的内存管理、逻辑控制以及图像形成，而让GPU负责大量的并行计算，包括卷积核函数的计算，栅格化过程的处理等，分工明确。

在GPU中进行栅格化处理时，使用原理为：同一基线连续测量的任意两个数据之间的时间间隔足够短，相同基线测量的数据集经过栅格化处理后将落在相同的网格点上。同时借鉴Romein[18]的研究成果，将栅格化分成与卷积核函数相同大小的子网格，线程被分配用来处理每个子网格中的可见度数据，并依靠基线轨迹，将数据进行累加并存储到GPU寄存器中。当基线轨迹移动到下一个网格点时，将当前网格点内的值进行累加取均值，并在处理下一个网格点之前，将当前网格点的处理结果从寄存器写入全局内存中[19]，这样能减少GPU内存的使用。

该方法利用基线进行并行化，将同一基线不同时刻的观测数据作为一组，每个线程负责处理一组数据。本文的加速方法所需的最小总线程数为：csmax×csmax×Nbaselines×Nfacets，其中csmax是cfullsupport数组中的最大值，Nbaselines为基线个数。此外，当卷积核全支撑大小较小时，每个线程将处理1个分面中1个基线的1次栅格化循环(即1个卷积点)，将最大限度地进行并行化，循环次数减少到只有2层循环；当卷积核全支撑大小较大时，每个线程将处理1个分面中1个基线的多个卷积点，因为每个线程块的最大线程数目通常在256～1 024之间。相对文献[12]，本文增加了分面的并行处理。为避免两个或多个线程发生竞争现象，我们对全局内存的写入方式设置为原子性。

由于实际观测的数据通常是按照时间顺序记录在表格文件里的，同一时刻包含不同基线的数据，为了进行基线并行化，必须对输入数据进行重新排序。首先将输入的数据按照不同基线分组并组成一排，然后对相同基线即一组内的数据集按照观测时间先后排序。对每组基线进行编号，该编号是0至Nbaselines-1的自然数。天线在数据文件中有唯一编号，因此可以通过下式计算出基线的编号iB[12]：

其中，iant1和iant2分别是该基线中天线1和天线2的编号，Nant天线个数，imin是天线1和天线2的编号最小值。

由于输入的数据一般已经进行过射频干扰的去除和校准处理，处理之后有些数据将会被删除，每组基线内的数据长度或时间步数(时间戳数目Nt)将会不同。因此，每组基线主要通过该组数据开始索引和时间戳数目循环(遍历)处理完该组的数据[12]。基线的开始索引可以通过下式计算得到[12]：

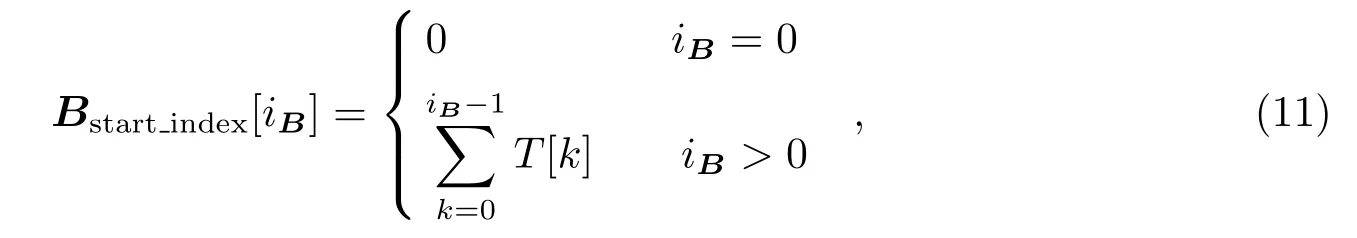
其中，T是由所有组基线时间戳数目构成的数组，数组的索引与每组基线的编号一致。

图1给出基于GPU的混合w-facets成像并行算法流程。图中主要分为主机处理、GPU处理和具体模块处理三个部分来描述。在单个GPU节点中算法优化的过程为：首先，主机读取数据集；然后主机与GPU设备进行通讯，完成GPU设备的初始化工作，包括选取性能最好的GPU卡和数据处理所需的内存的分配等；接着，将存储在主机内存中的数据进行重新排序，并将重排后的数据发送到已分配好的GPU内存中。其次，在GPU中以基线并行的方式进行数据处理，计算并行参数：根据线程索引计算出该线程所需要处理的基线起始索引iB、栅格化的卷积核全支撑索引(su和sv)和分面索引(j)。具体的计算方法，见式(12)。然后，利用计算好的索引，按照频率通道(c)和时间戳数目(Nt)两层循环，加载该线程所需要处理的数据，以及获取w核函数，并进行乘累加，从而完成基线的栅格化处理。循环结束后，即结束该线程的处理任务。最后，将栅格化后的数据返回到主机内存中，并对该数据进行逆傅里叶变换(IFFT)从而得到脏图。

其中，csw是w值对应的卷积核全支撑大小，thid是线程索引。

图1 基于GPU的混合w-facets成像并行算法流程

4 实验与分析

4.1 算法验证

本节采用的数据来自SKA先导望远镜MWA的银河系与河外星系全天巡天(galactic and extragalactic all-sky MWA survey,GLEAM)项目中于2013年8月9日22:13:18开始并历时112 s的快照观测数据，该快照观测的相位中心为(RA=03h13min54.40s,DEC=-55°04′02.82′′)，观测频率范围是200～231 MHz。首先我们对该观测数据进行RFI消除、频率与时间积分并转换为Measurement Set格式，然后进行校准处理，处理完后获得的数据将用于本文算法进行成像。

使用的测试环境是上海天文台SKA数据中心原型机的GPU节点，该节点具体的硬件指标参数如表1所示。

表1 上海天文台SKA数据中心原理样机的GPU节点指标参数

根据GLEAM巡天数据处理的经验，我们设置需要计算的脏图的大小为：4 000×4 000，每个像素的大小为25′′，因此脏图的最大宽度Iwidth约为0.48 rad。该快照数据的wmax值约为1 035倍波长，根据式(9)我们计算出单独使用w-projection时，最佳的Nwplanes约为248。如表2所示，是不同成像算法的测试结果对比。在成像质量对比方面，我们主要给出的是均方根(RMS)、动态范围(DR)和射电源识别数目。通过从这三方面的对比中发现，二维傅里叶变换方法(2D FFT，保持Nfacets=0和Nwplanes=0)成像质量最差，w-stacking方法成像质量最好。uv-faceting方法(保持Nwplanes=0)的成像质量比2D FFT好，随着Nfacets的增大成像质量越好。w-projection方法(保持Nfacets=0)在Nwplanes≥31时，成像质量均比2D FFT方法好；在较小Nwplanes时，w-projection比uv-faceting的成像质量要好，成像质量也随着Nwplanes的增大质量越高。对于w-facets方法的成像结果，在Nfacets=16和Nwplanes=62时质量最高；在相同的取值时，比单独使用uv-faceting或w-projection的质量都要高，并且最接近w-stacking的成像质量。此时，w-facets的图像动态范围比uv-faceting提高了2.34 dB，图像RMS降低了4 mJy·beam-1。在Nfacets=4和Nwplanes=124时，w-facets的成像结果比相同取值的uv-faceting成像质量好，比wprojection的差；在Nfacets=64和Nwplanes=31时，w-facets的成像结果比w-projection的都要好，与uv-faceting成像结果相近。成像质量的分析表明，uv-faceting与w-projection结合后，成像质量能够得到进一步提高。

在内存使用方面，我们记录了不同成像方法的卷积核内存使用情况或傅里叶变换(FFT)内存使用情况。w-stacking统计的是FFT内存使用量，其余方法均是统计卷积核内存使用情况，因为w-stacking的w项校正在图像域进行，卷积核消耗的内存小(小于1 MB)。由表2可知，2D FFT和uv-faceting的卷积核消耗的内存均小于1 MB，w-projection方法的卷积核内存消耗随着Nwplanes的增大而增大，且远远大于1 MB；w-facets方法的卷积核内存消耗随着Nfacets的增大而减少，当Nfacets=64时，内存消耗小于1 MB；w-stacking方法由于使用了较大的w层，FFT内存消耗较大，高达48 GB。分析表明，将w-projection与uv-faceting结合后，内存的消耗大大减少。

对于运行时间，我们给出的是使用20个CPU核的运行时间和使用1个GPU卡的运行时间，所有运行时间均是测量10次取平均值。由于基于多核CPU的并行是针对分面，因此仅使用w-projection方法时，程序是串行执行的，比uv-faceting方法消耗更多的时间。由于使用20个CPU核，uv-faceting方法在Nfacets=16时能够充分并行，所以消耗的时间都比其他的分面数少。w-facets方法在Nfacets=16和Nwplanes=62时，耗时最短，与相同w平面数的w-projection方法耗时相近，但耗时比uv-faceting方法均长。上述分析表明，uv-faceting结合了w-projection之后，运行时间会变长。使用了GPU加速后，大多数方法的运行时间整体大大缩减了；uv-faceting和w-facets的运行时间依然随着Nfacets的增大而变长；w-projection方法随着Nwplanes增大，运行时间无较大变化，因为GPU的加速方法主要是针对栅格化进行并行，因此分面数越大需要的处理时间越多。w-facets方法中GPU的运行速度比20个CPU核快7～33倍。

表2 测试结果对比

如图2和图3所示，分别为基于GPU的混合算法的成像结果和使用w-stacking算法的成像结果。为了便于比较，我们截取出距离原始图像较远位置的射电源，并得到如图2b)中和图3b)中的两个图像。图2b)图像的峰值为每束光309.5 mJy，RMS值为每束光23.7 mJy。图3b)图像的峰值为每束光311.9 mJy，RMS值为每束光21.8 mJy。结合表2与整个图像的对比，表明本文的GPU混合算法能够对距离较远的射电源成图，且成图结果与w-stacking获得的结果基本一致。基于多核CPU的混合算法结果与GPU混合算法结果相同，这里不作展示。

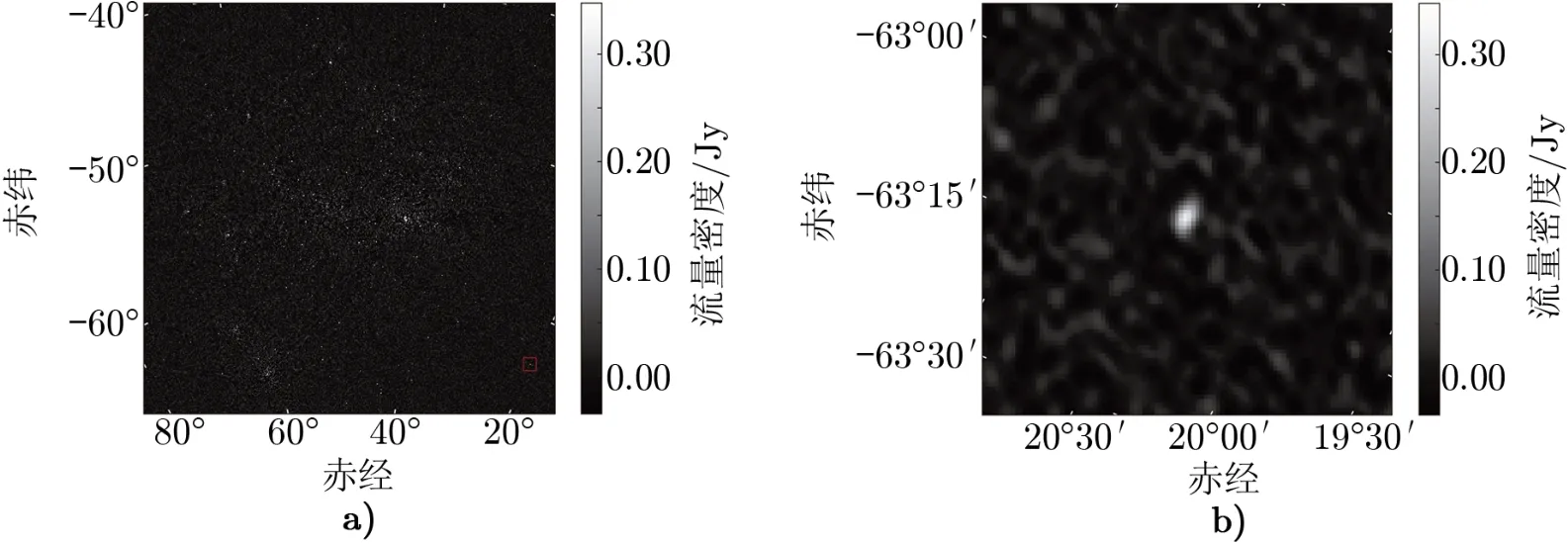
图2 基于GPU的混合w-facets成像并行算法的成像结果(Nfacets=16,Nwplanes=62)

4.2 性能测试与分析

性能测试部分采用模拟数据进行，主要使用牛津大学开发的SKA射电望远镜模拟软件(OSKAR)仿真并生成SKA1-low观测数据。主要的参数设置为：天线采用SKA1-low第四阶段的完整规模天线阵列，台站个数为512，基线个数为130 816，最长基线为65 km，观测相位中心为(RA=201.36,DEC=43.02)，偏振个数为4，波束个数为1，观测的起始频率为50 MHz，频率带宽为300 MHz，频率通道数为64，每个频率通道的带宽为4 687.5 kHz；积分时间为2 min，起始观测时间设置为2015年01月01日18点整，总观测时长为2 min。观测相位中心指向的天区包含一个巨大的射电星系NGC 5128，也称为半人马座A(Centaurus A)。它不仅是距离地球最近的射电星系(距离大约为11.09光年)，而且是南半球最大的星系。本模拟观测使用的天空模型是由包含Centaurus A的MWA GLEAM巡天图像制作得到[20]。该模型共有23 811个独立成分，包含23 336个高斯源和2 475个点源。所有成分的流量强度和谱指数分布在74～231 MHz频率范围内。最终模拟观测产生的数据量大小约为36 GB。该数据曾经作为SKA科学数据处理器工作包中基于执行框架的大视场成像流水线的性能测试[21]，因此比较适合用于本文的性能测试。

实验设置的成像参数是：脏图大小为1 024×1 024，每个像素大小为14.06′，Nfacets=36。该模拟数据的wmax=61 026倍波长，根据脏图的大小和分面数，我们计算出最佳的Nwpalanes=355。该部分的实验采用的测试环境与验证性实验相同。如图4所示，是性能测试的结果，主要使用了不同CPU核数(线程数)测试基于多核CPU方法的可拓展性，使用一个GPU卡测试基于GPU方法的加速性能。图中每个测试点的运行时间均是连续测试10次取平均值。我们根据图4计算出加速比情况，如表3所示。根据多核CPU的方法，当使用的线程数为36时，线程数与Nfacets值相等，因此消耗的运行时间最短；使用1个线程时，相当于串行程序，运行时间最长；线程数为1～12，消耗的运行时间近似线性减少；线程数大于12后，没有明显的线性关系，在线程数为24和36时，运行时间出现下降。使用V100 GPU时，单精度加速比为201.8，运行速度是36个线程数的8.9倍左右；双精度加速比为173.5，运行速度是36个线程数的7.7倍左右。上述分析表明，基于多核CPU的方法在少量线程数内有一定的可拓展性，当线程数与Nfacets相等时，运行速度最快；基于GPU的方法在运行速度上比多核CPU方法有明显的优势。

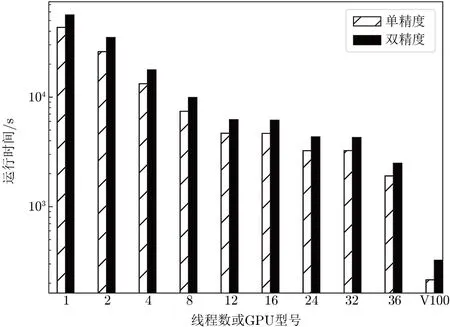
图4 混合w-facets成像并行算法性能测试结果

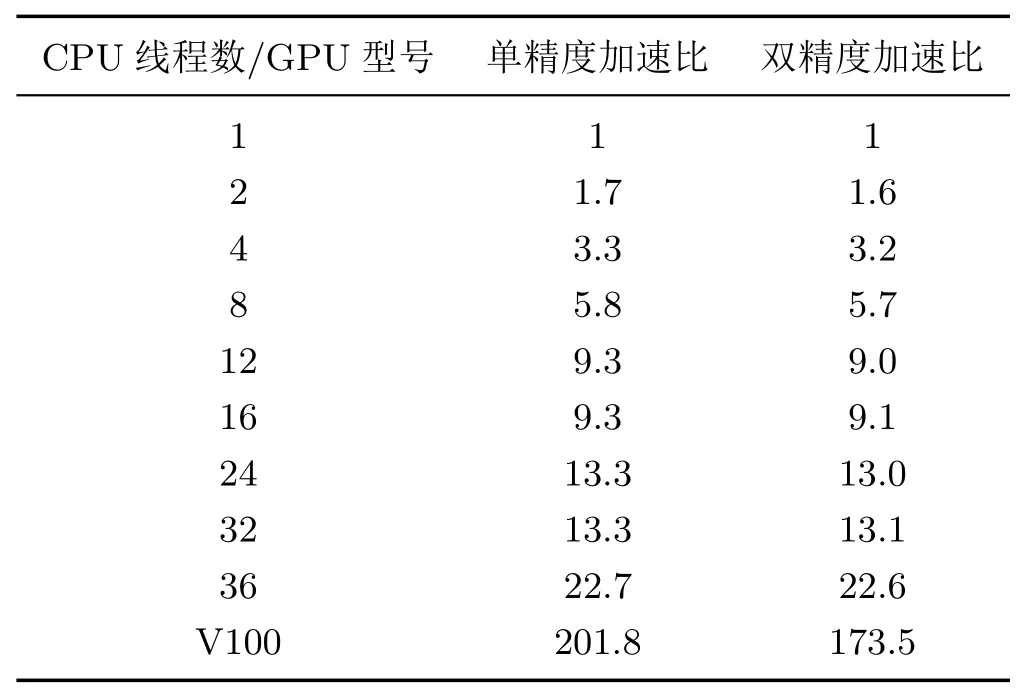
表3 加速比情况

5 总结与展望

由于低频射电望远镜阵列对成像具有高动态范围和高分辨率的要求，因此面对海量天文观测数据时，既须保证大视场成像的成图质量也必须具有较快的运行速度。故本文研究了uv-faceting与w-projection相混合的算法，称为w-facets算法，为将来开展低频射电望远镜阵列巡天观测的数据处理提供技术手段。与uv-faceting算法相比，w-facets算法能够进一步减少噪声水平，提高成图的动态范围，改善成像质量；与w-projection算法相比，w-facets算法大大减少了内存的消耗，提高了可拓展性。w-facets在uv-faceting的基础上使用w核进行栅格化，运行时间比uv-faceting慢很多，但与w-projection的运行时间相近。为此，本文提出了两种并行优化方法：基于多核CPU的混合w-facets成像并行方法和基于GPU的混合w-facets成像并行方法。通过图像验证性实验和性能测试实验表明，本文提出的两种方法均能够正确实现混合w-facets算法成像，并提升混合算法的成像速度。基于多核CPU的并行加速方法运行速度最大提升约22.7倍，基于GPU的并行加速方法运行速度最大可以提升约201.8倍；这表明基于GPU的并行加速方法比基于多核CPU的并行加速方法更高效。但是通过本文测试分析可知，基于多核CPU的并行加速方法效果略差，因为采用的是粗粒度的并行方法，后续工作将考虑通过更细粒度的CPU并行方案进行优化。