激光干涉引力波探测器的参量不稳定性问题及其研究进展
吴斌,刘见,张珏,陈旭
(1.北京师范大学天文系,北京100875;2.Albert Einstein Institute,Hanover 30167;3.Department of Physics,University of Western Australia,Crawley 6009)
1 引言
1.1 激光干涉引力波探测器
激光干涉引力波探测器由两条相同的干涉臂组成,它利用干涉原理,通过测量两条干涉臂由引力波引起的长度变化差来探测引力波信号。一般情况下,引力波传播到地球时的振幅已变得非常小(约能引起千米级别的干涉仪的臂长变化,原子核尺寸的1‰)。为了测量到该微小的长度变化,激光干涉引力波探测器在普通的迈克尔逊干涉仪的基础上做了许多改进[1–3]。以美国的激光干涉引力波天文台(Laser Interferometer Gravitational-wave Observatory,LIGO)为例[1],它的干涉臂长为4 km,且每一条臂都是由两个测试物质组成的法布里-珀罗谐振腔,被称为探测器的臂腔。臂腔的两测试物质之间的距离变化则体现了干涉臂的长度变化。利用臂腔,激光在测试物质间来回反射,这极大增加了干涉仪的有效臂长,因此引力波给干涉仪带来的微小形变被积累放大。除此之外,另有两个重要的改良是功率循环和信号提取技术的引进,它们分别增加了臂腔内的循环功率和拓宽了探测的频率带宽。自2015年以来,高新激光干涉引力波天文台(advanced LIGO)在已完成的两轮探测(O1和O2)中,共探测到11个引力波信号[4],其中包含了首次双中子星并合事件[5]。始于2019年4月的为期近一年的第3次探测(O3),探测了更多更远的信号[6,7]。在O3观测阶段,Advanced LIGO对双中子星并合事件和双黑洞并合事件的观测距离分别可达到120 Mpc和1 100 Mpc左右,而在O1和O2观测阶段的Advanced LIGO对双中子星并合事件的探测距离分别为80 Mpc和100 Mpc,对双黑洞并合事件的探测距离分别为740 Mpc和910 Mpc[8]。
量子噪声是目前限制引力波探测器灵敏度的主要因素之一。它包含两种噪声[9]:低频段由辐射压噪声主导,它来源于光子对测试物质辐射压力的涨落,这会导致测试物质的位移噪声;高频段由散粒噪声主导,它来源于光子抵达光电探测器的时间与光子数量的不确定性[10]。探测器臂腔内激光的功率对两种量子噪声的强弱有相反的影响:若提高激光功率,辐射压噪声会变强,但散粒噪声会减弱。为了将辐射压噪声和散粒噪声折中,并将量子噪声合理地降至最低,激光干涉引力波探测器在不同探测频率下会有一个最佳的激光功率。根据Advanced LIGO的设计,其臂腔内循环功率要达到约8×105W[1]才能使探测器在百赫兹附近达到最佳的灵敏度。在O3观测阶段的Advanced LIGO,臂腔内的激光功率约为2×105W[11],与全功率相差很大。
1.2 参量不稳定性问题的提出及目前的研究概况
影响激光干涉引力波探测器的干涉臂内激光功率的重要因素,是臂腔内光学模与测试物质的机械模(声学模式)之间相互作用引起的参量不稳定性。在参量不稳定性出现时,臂腔内的激光能量可以被传递到测试物质的机械振动中,最终影响干涉仪的稳定工作。
Braginsky等人[12]在2001年首次提出高功率激光在激光干涉引力波探测器臂腔中的使用会带来参量不稳定性问题,他指出参量不稳定性会影响干涉仪臂腔内所能存储功率的上限,并强调了解决参量不稳定性问题的重要性。随后Zhao等人[13]对激光干涉引力波探测器中的参量不稳定性问题进行了进一步的理论研究和数值模拟,并对Advanced LIGO的参量不稳定性进行了预测。Zhao等人在文章中还提出利用热形变来改变探测器测试物质的曲率半径,可以在一定程度上抑制参量不稳定性[13]。之后,越来越多的研究小组加入到参量不稳定性的研究当中[14–18],更贴合大型激光干涉引力波探测器实际情况的理论计算和模拟详细地给出了一系列不稳定模式的频率[19],并进一步揭示了参量不稳定性问题在引力波探测中的重要性。Advanced LIGO在2015年首次观测到了参量不稳定性现象[20],该实验结果证实了Zhao等人的预测。
在Advanced LIGO的前两轮探测中,参量不稳定性主要通过两种方法来抑制:最初采用的便是Zhao等人提出的利用热形变改变测试物质曲率半径的方法;另外一种方法是通过静电驱动来主动控制测试物质的振动[21]。这两种方法都存在一个弊端:它们很难同时抑制多个不稳定的模式。而在全功率运作的条件下,Advanced LIGO的每一个测试物质都会有10个左右的不稳定模式[20],所以多个模式的同时抑制很重要。在O3观测中,Advanced LIGO采用了一种实施起来更加简单但十分有效的新方法——声学模阻尼器[22]。这一新方法在O3观测中抑制了(1.5~1.8)×104Hz宽带内的参量不稳定性,但它的难点在于抑制参量不稳定性的同时在引力波信号频段不出现额外的热噪声。未来,激光干涉引力波探测器臂腔内的激光功率将持续增加,会出现更多的不稳定模式;设计覆盖频段更宽、阻尼更大的阻器是人们面临的挑战。
本文将从参量不稳定性的原理出发,详细介绍以上几种比较重要的解决参量不稳定性问题的方法,之后将结合目前对于参量不稳定性问题的研究进展,介绍三种值得继续研究的新方法。
2 参量不稳定性
2.1 光声相互作用
光声相互作用是导致参量不稳定性现象的根本原因。从光子和声子的角度,该相互作用可以用斯托克斯过程和反斯托克斯过程来解释。如图1a)所示,一个频率为ω0的光子被散射,产生了一个频率为ωs的更低频的光子和频率为ωm的声子,这一过程被称为斯托克斯过程;如图1b)所示,一个同样频率为ω0的光子被频率为ωm的声子散射,产生一个频率为ωa的更高频的光子,这一过程被称为反斯托克斯过程。在激光干涉引力波探测器的臂腔内发生的光声相互作用,实际的效果常常是将臂腔内基模的能量散射到了不同频率的高阶模上。如果散射出来的高阶模能在臂腔内谐振,臂腔内便能产生两个光学模式(基模和高阶模)与一个声学模式之间的三模相互作用。
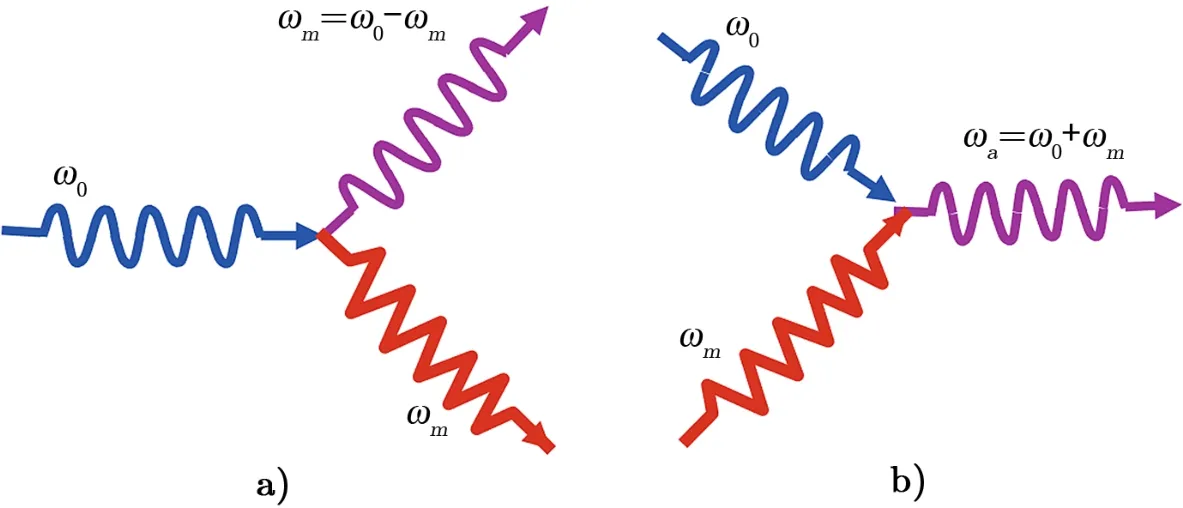
图1 斯托克斯过程与反斯托克斯过程[23]
图2从经典力学的角度解释了三模相互作用,臂腔内的基模(ω0)能量,被测试物质某个特定的声学模式(ωm)散射到高阶模(ω1)上。通过辐射压的形式,臂腔内的光学基模与高阶模之间的拍频会给测试物质施加一个带有特定空间分布的力,从而引起测试物质的振动。当测试物质的声学模式和臂腔内的两个光学模满足以下两个条件的时候,会出现较强的三模相互作用:其一,测试物质的声学模频率与光学模的模式间隔(光学基模与高阶模之间的频率差)满足频率匹配条件,即|ω0-ω1|≈ωm;其二,散射出来的高阶模的电场的能量分布与测试物质的声学模式的振幅分布之间有足够大空间重叠。在Advanced LIGO的臂腔内,一些光学模与测试物质的声学模有较大空间重叠,如图3所示。由于测试物质的曲率半径在沿表面的不同方向上有微小差别,它不再是中心对称的,所以图中每种模式有两种形式(强度分布旋转90°,频率略有差别)[19]。
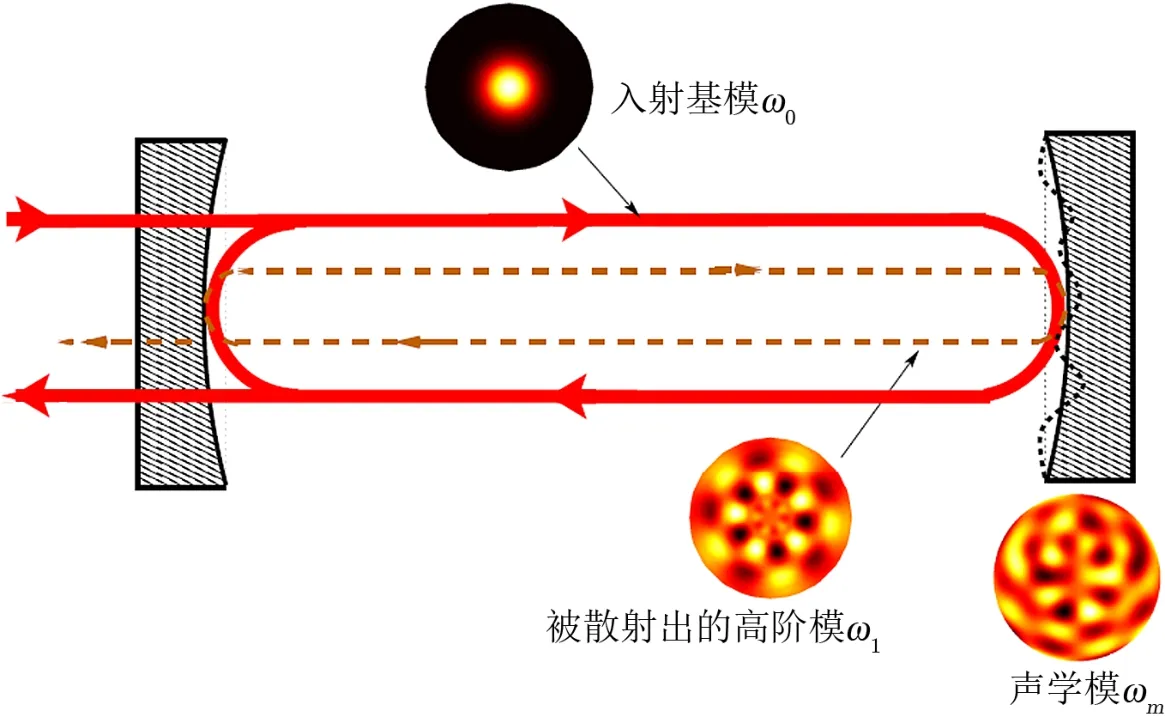
图2 经典力学角度的三模相互作用[24]
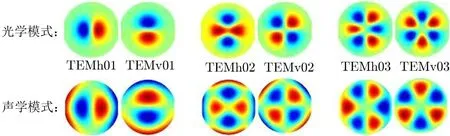
图3 光学模式与声学模式分布的空间重叠[19]
2.2 参量增益
人们通常使用参量增益因子R来更加直观地描述三模相互作用[25]。对于激光干涉引力波探测器的臂腔来说,参量增益因子的定义如下:
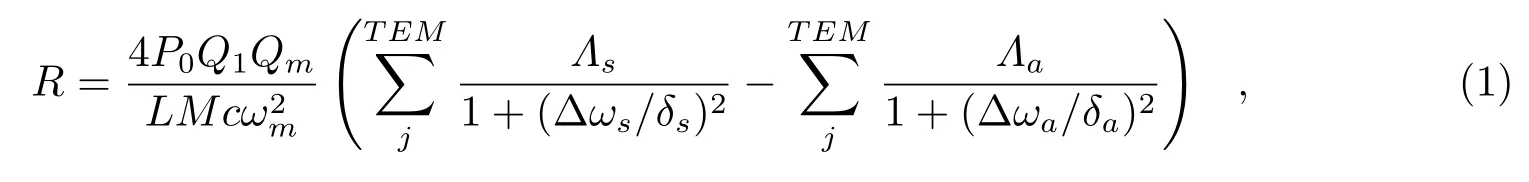
其中,P0代表臂腔内基模(TEM00)的能量;Q1和Qm分别代表臂腔内光学模和测试物质声学模的品质因子;L是臂腔的腔长;M是测试物质的质量;c是真空中的光速;ωm是测试物质声学模的频率;Δωs和Δωa反映了前文所提到的频率匹配情况,Δωs/a=|ω0-ωs/a|-ωm;δs与δa分别是斯托克斯模和反斯托克斯模的线宽。可以看出,能量从光学模式传递到声学模式的斯托克斯过程,降低了光子的频率并激励了声学模式的振动,参量增益因子为正;能量从声学模式传递到光学模式的反斯托克斯过程,升高了光子的频率并阻尼了声学模式的振动,参量增益因子为负。Λ代表高阶模光场分布与测试物质声学模振幅分布的空间重叠,下标s和a分别对应斯托克斯模和反斯托克斯模,Λ表达式为[12]:

式中V代表臂腔的体积;E00和Emn分别代表臂腔内基模和高阶模的电场分布;r代表三维的空间坐标矢,r⊥为r垂直于测试物质表面的分量;μ代表测试物质声学模的空间位移情况,μ⊥为μ在垂直于测试物质表面的分量。Λ的取值越大,代表模式之间的重合度越大。
在发生三模相互作用时,测试物质的振幅随时间按指数et/τpi变化。利用参量增益因子R,测试物质振动的时间常数τpi可以表示为[22]:

其中,τm是在没有三模相互作用的情况下测试物质振动的时间常数,仅与测试物质的品质因子Qm相关:Qm=τm×ωm/2。
可以看出,当R<1的时候,时间常数是负数,这意味着测试物质的振幅随着时间指数衰减,衰减的时间可能比正常的弛豫时间短或者长;当R>1的时候,时间常数为正数,测试物质的振幅会随着时间指数型增长,即出现不稳定的情况;而如果R=1,三模相互作用带给测试物质的能量与测试物质自身的能量耗散相等,此时τpi-→∞,即测试物质将保持不变的振幅永远振动下去。
相对于Initial LIGO,测试物质声学模和光学模的品质因子也分别增大了10倍和2倍。从式(1)可以看出,参量增益的倍数与P0,Qm和Q线性相关,这3个量的变大,大大增加了参量不稳定性出现的可能性。于是在2015年,Advanced LIGO一开始工作便发现了参量不稳定性现象。在LIGO之前,也有其他一些相对小型的实现验证了参量不稳定性理论的正确性[27,28],这些实验对LIGO这样的大型引力波探测器中可能出现的问题有很重要的指导意义。
3 参量不稳定性的抑制
抑制参量不稳定性其实就是要把参量增益R控制在1以下。从参量增益的表达式(1)中我们可以发现,通过改变引力波干涉仪的某些参量,可以达到降低参量增益的效果。其中最简单直接的办法是降低臂腔内的激光功率,但是为了维持散粒噪声水平,臂腔内的高功率激光不可或缺。目前理论和实验上比较可行的几种办法,主要是通过改变光学模和声学模的频率匹配情况或降低测试物质的品质因子来降低参量增益。
3.1 环形加热器
参量不稳定性出现的要求之一是满足频率匹配关系,即前文所提到的基模与高阶模之间的模式间隔与声学模频率相等。对于激光干涉引力波探测器的臂腔来说,该模式间隔可以通过理论计算出来[26]:

其中,ωmn代表高阶模的频率,ω00代表基模的频率,c是真空中的光速,L是臂腔的腔长,m和n是高阶模的横模指数。g1和g2分别由下面的两个表达式得到:

其中,R1和R2分别代表测试物质的曲率半径。一个稳定的臂腔必须满足0<g1g2<1。
由式(4)和(5)可知,若改变测试物质的曲率半径,臂腔内的模式间隔将会随之发生改变,这便是环形加热器(ring heater,RH)的原理。环形加热器的概念如图4所示,环形的热源与测试物质没有直接接触,它环绕在测试物质边缘,通过热辐射给测试物质加热。由于边缘吸收的热量多、形变大,测试物质的曲率半径因此降低,这一曲率半径的变化直接影响到臂腔的g因子,从而改变了臂腔内高阶模与基模之间的频率差。若频率变化超过臂腔的线宽,频率匹配关系被打破,三模相互作用无法得到加强,参量不稳定性便被抑制住。
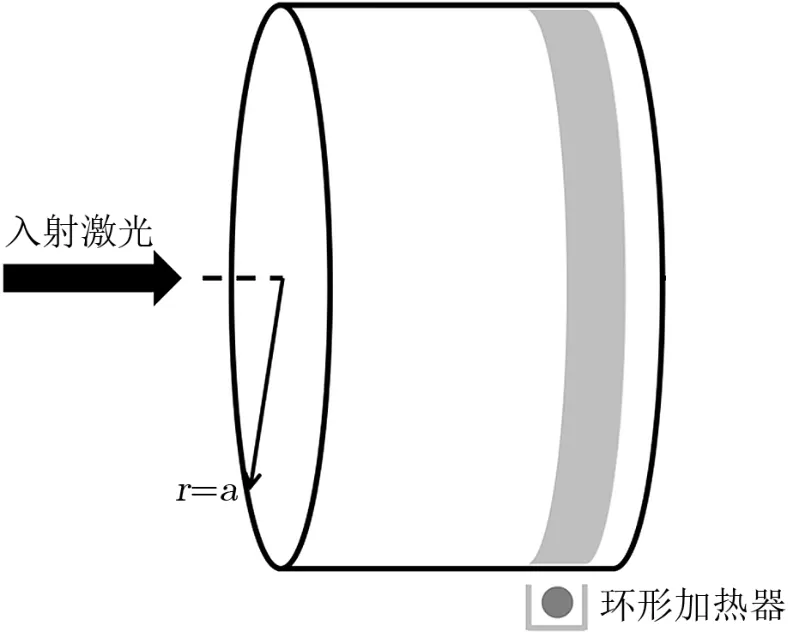
图4 环形加热器概念图[29]
Advanced LIGO测试物质曲率半径约为2 km,对于臂腔内的三阶模(TEM03)而言,测试物质曲率半径变化1 m就足以将它的频率改变80 Hz,约等于臂腔的一个线宽。对于简单的法布里-珀罗谐振腔来说,一个线宽的频率移动,可以将参量增益降低一半,而对于采用了功率循环和信号提取技术的引力波探测器,变化更为显著[30]。在LIGO Livingston首次发现其臂腔内的参量不稳定性现象后不久,环形加热器便被用于参量不稳定性的抑制。在测试物质曲率半径变化了2 m之后,参量增益降到了1以下,整个探测器在臂腔内激光功率接近1×105W的状态下稳定工作超过12 h[20]。值得注意的是,这并不是环形加热器首次在LIGO投入使用,在此之前它被用来抵消由于测试物质吸收基模的能量而引起的曲率半径的变化[31],并且最高可以实现几十米曲率半径的改变[32]。
若LIGO工作在其设计功率下,采用环形加热器抑制参量不稳定性现象将会有一定的限制。因为随着激光功率的增高,一方面参量增益也呈线性增大,环形加热器将不足以将这些大的增益降到1以下;另一方面不稳定模的密度也会变大,这时候把一个模移开其不稳定区域的同时会有极大的可能性将其他原本稳定的模式移动到不稳定的区域中。
3.2 静电驱动器
光学模产生的辐射压对于测试物质的推动,需要大于测试物质自身的耗散才能够激发参量不稳定性。从式(1)可知,参量增益R与测试物质的品质因子Qm呈线性相关,所以降低测试物质的品质因子是抑制参量不稳定性的另一个方向。
Ju等人[23]2009年首次提出可以利用静电驱动器(electrostatic drive,ESD)来抑制参量不稳定性,随后Miller等人[33]在LIGO对静电驱动做了进一步研究。2016年Blair等人[21]在LIGO Livingston首次实验证实了静电驱动在抑制参量不稳定性问题中的可行性。如图5所示,静电驱动的基本原理是通过反作用质量(reaction mass,RM)上排列的梳齿状的导体,给测试物质提供一个与其振动频率相同、相位相反的纵向驱动力来抵消三模相互作用对测试物质的辐射压。本质上,它是一个通过实时的反馈回路控制测试物质,从而有效地降低测试物质的品质因子的主动阻尼过程。为了达到理想的驱动效果,该驱动力的分布也需要与测试物质的声学模式有较大的空间重叠。

图5 Advanced LIGO静电驱动装置的模拟图[21]
图6所示的是Advanced LIGO的静电驱动系统反馈回路的简图。竖直方向干涉臂的透射光被一个四象限的光电探测器收集,该四象限光电探测器可以测量到臂腔内基模(TEM00)和三阶模(TEM03)之间的拍频信号,该三阶模是被测试物质的一个声学模(15.54 kHz)散射出来的。拍频信号先通过一个15.54 kHz的带通滤波器以及一个放大倍数可调的放大器,再经过移相器之后被传输到静电驱动器上。通过该反馈驱动过程,Advanced LIGO把这个TEM03模所对应的参量增益从2.4降到了0.18[21],施加在测试物质上的静电力从测试物质振荡最严重时的0.62 nN,降到了稳态时的0.03 nN[21]。

图6 Advanced LIGO的静电驱动系统反馈回路简图[21]
静电驱动方法同样会在臂腔内激光功率增大时遇到难以解决的困难。如随着激光功率增大而新出现的不稳定模式可能与静电驱动力的分布仅有很小的空间重叠,因此,即使是一个很小参量增益,也需要非常大的驱动力来抑制。Miller等人[33]的模拟结果显示,在30~90 kHz频段内出现的一些不稳定模式,可能需要比目前大30倍的静电力来抑制。与此同时,每一个不稳定模式将会对应一个独立的控制信号,这意味着随着不稳定模式的增加,反馈回路的设计也将变得异常复杂。
3.3 声学模阻尼器
在最近的O3观测中,被动阻尼的方法在抑制参量不稳定性中取得了很好的效果。不同于主动阻尼的反馈控制,被动阻尼是通过在测试物质上安装一种声学模阻尼器(acoustic mode damper,AMD)而实现了宽带内测试物质品质因子的降低。
设计一个符合要求的被动阻尼器比较困难,一方面它需要在15~80 kHz的宽带里实现有效的阻尼,另一方面它要确保在激光干涉引力波探测器的探测敏感频段(100 Hz附近)不带来新的噪声。Gras等人[34]在2010年研究了一种金属环阻尼器,这一方法可以有效地将大部分不稳定模式的参量增益降低98%,但它存在两个弊端:其一,金属环阻尼器并不是对所有的模式都有同样的效果,对于一些特定模式它只有很弱的抑制效果;其二,在有效地降低参量增益的同时,金属环阻尼器引入了无法忽略的热噪声,从而影响探测器的灵敏度。随后在2015年,Gras等人又设计了一种新的阻尼器——声学模阻尼器[35]。这种阻尼器能够实现宽带宽(15~80 kHz)的阻尼,但在100 Hz左右也会引入约为初始状态2倍的热噪声。在此基础上,Biscans等人[22]在2019年改良了阻尼器中的元件,使其不再对激光干涉引力波探测器的热噪声水平造成明显的影响,并在LIGO的O3观测中投入使用。在LIGO的臂腔内,当激光功率达到设计功率的30%时,新的声学模阻尼器将消除15~80 kHz内所有可能出现的不稳定情况。
声学模阻尼器的关键元件是一个压电陶瓷,它把测试物质的应变能转化为电能,最后通过电阻以热能的形式耗散掉。这样一个耗散系统,本质上是一个损耗很大的弹簧,声学模阻尼器(AMD)可看作是该弹簧与连接在该弹簧上的小质量物体的组合。而在考虑被隔震系统悬挂起来的测试物质(TM)时,我们可以认为它是通过一个几乎没有损耗的弹簧连接在固定的墙壁上,因此阻尼器与测试质量组成的系统构成了一个质量比很大的耦合振荡器,图7是其简化的概念模型。通过选择合适的阻尼器(损耗很大、质量很小且其共振频与测试物质共振频一致),系统的品质因子便可减小到足以将参量增益降低到1以下。为了实现宽带宽阻尼,Advanced LIGO的每一测试物质上都安装了4个针对不同频段的阻尼器,对于阻尼器没有覆盖到的10 kHz频段的2个不稳定的模,则采用3.1节中所提到的环形加热器来抑制。

图7 被动阻尼的概念模型[22]
声学模阻尼器在Advanced LIGO的O3观测中发挥了很重要的作用,但未来阻尼器的使用将同样面临一些问题。一方面,随着激光功率的提升,臂腔内会出现更多其他频率的不稳定模式(在15~80 kHz频段之外),现有的不稳定模式的参量增益也会随之变大,针对新的频率以及更大的参量增益设计新的阻尼器将是一项新的挑战;另一方面,未来的引力波探测器的热噪声将会变得更低,这意味着由声学模阻尼器引入的热噪声虽然在目前可以忽略,但是在未来将不可忽略。
3.4 阵列加热器
阵列加热器常被用来修正激光干涉引力波探测器测试物质的面形误差。以意大利的引力波探测器Advanced Virgo为例,Day等人[36]通过阵列加热器使测试物质表面受热并发生形变,实现了对面形误差的实时修正,从而最大限度地保证了臂腔内激光不被散射到其他模式上。阵列加热器也能用来解决参量不稳定性问题,它的出发点与环形加热器类似,都是通过改变臂腔内的模式间隔,从而改变臂腔内的频率匹配情况来打破三模相互作用。不同的是阵列加热器可以对测试物质表面进行小区域的加热,从而达到随意改变表面形状的目的。
改变测试物质表面的形状实际上是改变了臂腔的体积。根据能量守恒定律,臂腔体积变大相当于臂腔内光子对外做功,光子能量降低,对应着频率的降低;反之,体积变小相当外界对光子做功,光子能量增大,对应着频率的升高[37,38]。利用这一关系,测试物质表面形变与臂腔内光学模的频率变化被联系了起来,我们可以利用一个转换矩阵来实现它们之间的转换:

其中,A代表测试物质表面形变,它是以泽尼克多项式为基底将表面形变分解得到的系数,泽尼克多项式是常被用来拟合光学表面的一组正交完备基;ω代表不同高阶模所对应的模式间隔的变化量;T是转换矩阵,矩阵的m行n列的元素Tmn代表的是第m个高阶模在形如第n个泽尼克多项式的形变之下的模式间隔变化量。利用T的逆矩阵,我们便可以通过设计特定的测试物质表面形变(A)来调整臂腔内任意的模式间隔(ω),这为同时抑制多个不稳定模式提供了可能,也能够保证在抑制一个不稳定模式时不会引入新的参量不稳定性。
目前阵列加热器还没有用于实验中参量不稳定性的抑制,但理论计算和模拟结果已初步证明了该方法的可行性。图8显示了利用转换矩阵导出的一个测试物质表面形变,该形变能够在将TEM03模的模式间隔变化100 Hz的同时维持其他的模式间隔不变。
阵列加热器能够同时控制臂腔内的不同模式间隔,这一点比环形加热器具有更明显的优势,图9显示了阵列加热器与环形加热器改变模式间隔的效果对比。在不使用加热器时,蓝色虚线显示,在15 kHz附近的光学模间隔与蓝色箭头指向的声学模频率相匹配。采用环形加热器和阵列加热器都能够将该模式间隔往左移动,从而避开这个不稳定的频率区域。但是在图9所示的情况下,环形加热器将一个高阶模间隔从蓝色箭头指向的不稳定模式移开的同时,又将另两个高阶模间隔移向了红色箭头所指向的两个声学模式。而采用阵列加热器不会改变其他的模式间隔,从而不会引入新的参量不稳定性情况。
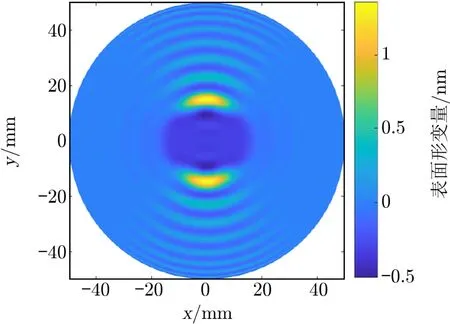
图8 利用转换矩阵导出的测试物质表面形变
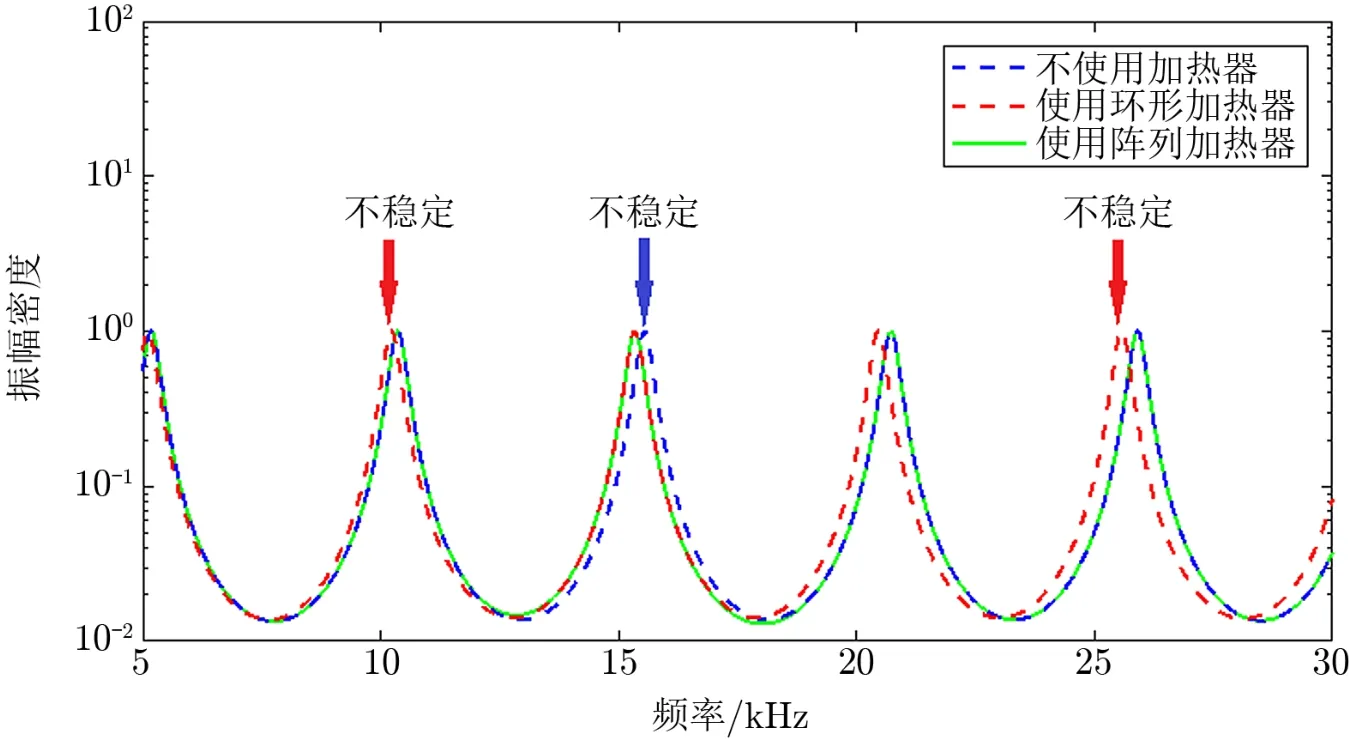
图9 阵列加热器与环形加热器的效果相比
要在实验上真正实现利用阵列加热器控制模式间隔还有很多工作要做。首先,不同的臂腔内支持的光学模式的光场分布不一样,这意味着针对不同的臂腔会有不一样的转换矩阵,测量测试物质上不同光学模光场的分布将是该实验的第一步;其次,模拟结果显示矩阵加热的结果与目标形变之间有一定的误差,这将给干涉仪引入新的损耗。除此之外,减少阵列加热器中加热元件的个数也是值得进一步研究的方向。
值得注意的是,转换矩阵与阵列加热器在光学实验中还可能有其他用处。因为臂腔内的模式间隔是可测量的,所以我们可以通过测量臂腔内模式间隔的变化来实时监测测试物质表面形变的情况,必要时还可通过阵列加热器来抵消该形变。
3.5 光学反馈
光学反馈(optical feedback)为抑制激光干涉引力波探测器臂腔内的参量不稳定性提供了另一条思路。当臂腔内的三模相互作用发生时,测试物质的振动信息会耦合到臂腔的反射光场中。光学反馈正是利用反射光场中的信息,生成了一个与臂腔内原有高阶模频率和空间分布都一致但是相位相反的光学模式,并将其注入到臂腔中。这样一来,臂腔内高阶模强度由于干涉相消而被减弱,参量不稳定性也因此被抑制。
光学反馈最初由Zhang等人[39]提出,随后Fan等人[40]通过实验进一步证明了该反馈系统可用于降低臂腔内的高阶模强度,实验结果如图10所示。在未开启光学反馈系统时,臂腔内TEM01模对应信号的强度达到了约42 mV,而在开启了光学反馈系统之后,TEM01模对应信号的强度降到了5 mV附近。值得指出的是,该实验并不是在参量不稳定性发生的情形下完成,实验中测试物质的振动是由外界驱动的,所以光学反馈对参量不稳定性的抑制效果,还有待进一步实验验证。
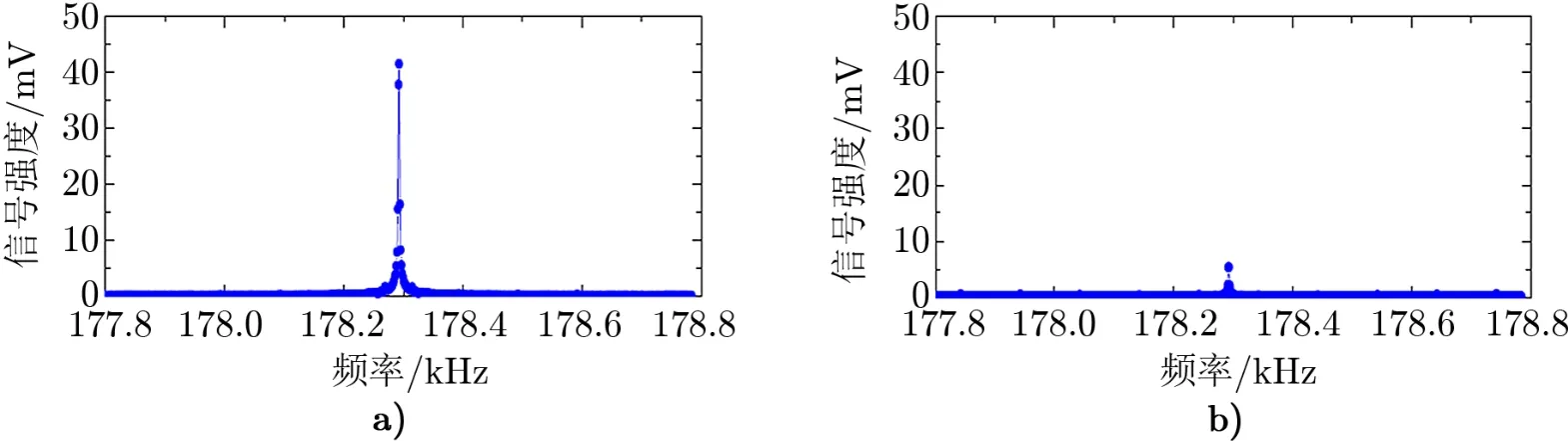
图10 臂腔内TEM01模对应的信号强度[40]
3.6 设计不存在参量不稳定性问题的新一代干涉仪
由前面的介绍可知,对于已建好的干涉仪,我们只能通过一些外加的装置在有限的范围内调整测试物质的曲率半径或者品质因子。但是如果设计新的干涉仪,我们可以根据模拟结果设计合适的臂腔参数,从而避免出现参量不稳定性。
Zhang等人[41]最近研究并模拟了臂腔腔长、测试物质直径以及测试物质曲率半径的设计对参量不稳定性现象的影响。他们的模拟结果指出,对于一个测试物质直径为50 cm的长8 km的臂腔,当测试物质的曲率半径在4 500 m附近约6.8 m的范围内变化的时候,臂腔内将不会出现任何不稳定的模式。如图11所示,在曲率半径约为4 500 m时,不稳定性模式缺失的情况。被称为“零参量不稳定性窗口”(PI-free window)。通过进一步优化,他们发现当臂腔腔长设计为6 335 m、测试物质直径设计为52 cm的时候,零参量不稳定性窗口可拓宽到45.1 m。当臂腔内激光功率增大时,零参量不稳定性窗口相应地变窄,甚至会出现不存在任何零参量不稳定性窗口的情况。但是,即便是在这种情况下,仍可以通过设计臂腔的参数来获得一些“低参量不稳定性窗口”,这可以减轻其他抑制参量不稳定方法的负担。
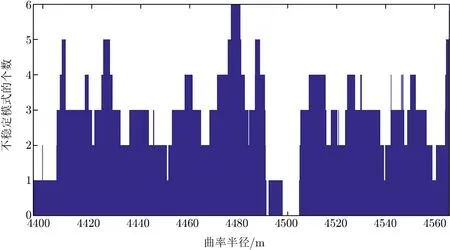
图11 零参量不稳定性窗口[41]
4 总结与展望
激光干涉引力波探测器的参量不稳定性问题是由臂腔内的光学模与测试物质的声学模之间相互作用导致的,这一相互作用会使得测试物质的声学模振动呈指数型快速增长,最终使得测试物质失去控制,探测器无法正常工作。根据参量不稳定性问题的产生原理,目前比较成熟的抑制参量不稳定性问题的方法主要基于两个出发点:其一,打破声学模式与光学模式之间的频率匹配关系;其二,降低声学模式的品质因子。
LIGO先后采用过三种方法来抑制参量不稳定性现象:环形加热器、静电驱动器和声学模阻尼器。其中环形加热器是利用测试物质的受热形变来改变它的曲率半径,从而改变臂腔内光学模式的间隔,使之不再满足频率匹配关系。静电驱动器通过实时的反馈回路,将测试物质控制在其平衡位置。声学模阻尼器在宽带内有效地降低了测试物质的品质因子,LIGO在O3观测中通过声学模阻尼器解决了15~80 kHz频带范围内所有潜在的参量不稳定性问题。
以上列举的这些方法在完成他们的设计任务的同时,也有一些不足之处。环形加热器在抑制一个参量不稳定性模式时,会将其他模式移入新的不稳定频段;静电驱动器的一个反馈回路只针对一个不稳定模式,若要同时抑制多个不稳定模式,反馈回路以及驱动力的设计将会非常困难;而要设计覆盖频段更宽、阻尼效果更好的声学模阻尼器也是一项新的挑战。
除了以上三种LIGO已采用的方法,本文还介绍了三种在未来值得进一步研究的新方法。(1)利用一个连接测试物质表面形变和臂腔内光学模式间隔的转化矩阵,设计能够产生特定模式间隔变化的测试物质表面形变,并通过阵列加热器在测试物质表面产生这一设计的形变。该方法解决了环形加热器带来的改变测试物质曲率半径会引入新的参量不稳定性的问题,但自身也还有一些不成熟的地方有待实验的进一步验证和提升。(2)采用光学反馈,通过向臂腔内注入一个与臂腔内已存在的高阶模相位相反但是频率和空间分布都相同的光学模式,来降低臂腔内的高阶模强度。(3)从激光干涉引力波探测器的设计出发,通过巧妙地选择臂腔的腔长、测试物质的尺寸和曲率半径,使得在一些特定的参数下“零参量不稳定性”工作状态成为可能。
在未来的激光干涉引力波探测器中,随着臂腔内激光功率的增大,可能的不稳定模式会越来越多(若使用Advanced LIGO的设计功率,臂腔内将会有超过40个可能的不稳定模式),与此同时,已有的不稳定模式的参量增益也会变大。在优化已有的抑制方法的基础上,多种抑制方法的共同使用,将会是抑制参量不稳定性问题的一个重要方向。
致谢
感谢西澳大学(The University of Western Australia)赵春农教授和鞠莉教授的宝贵意见,他们提供的资料充实了文章内容。同时也非常感谢审稿人和编辑部,他们的工作帮助提升了本文的质量。

