滑块在粗糙斜面内的平抛运动再研究

邵 云

(南京晓庄学院 电子工程学院，江苏 南京 211171)

文献[1]曾经对滑块在粗糙斜面内的平抛运动做了较为深入的研究，但仍留下一些缺憾。比如，由于当初计算机技术尚未普及的缘故，文献[1]未能给出滑块在空间的轨迹图像及对比；又如，可能由于篇幅的缘故，文献[1]也未能对滑块的速度分量及运动细节等进行进一步的讨论与论证；另外，文献[1]对于特殊情况下滑块解析形式的轨迹方程和运动方程的讨论也略欠系统，所枚举的例子尚不够全面。尽管如此，文献[1]不愧是一篇佳作，尤其是积分变量的选择，使得相关的积分变得异常简单，其中蕴含的变换技巧意味深长！笔者在下文中仍将沿袭该积分思路，从个人认识的角度，继续对滑块在粗糙斜面上的平抛运动进行分析和研究，籍以对文献[1]形成补充。

1 滑块在粗糙斜面内的平抛运动的动力学分析

如图1所示，现设一质量为m的滑块在倾角为α的粗糙斜面上以初速度v0沿斜面做平抛运动，斜面的滑动摩擦系数为μ。在重力沿斜面向下的分力G1和滑动摩擦力f的共同作用下，滑块将沿斜面向前下方做曲线滑动，如图2所示。设滑块在任意t时刻的速度为v，v与斜面上水平x轴正方向的夹角为θ，与沿斜面向下的y轴正方向的夹角为φ，显然有φ=π/2-θ。

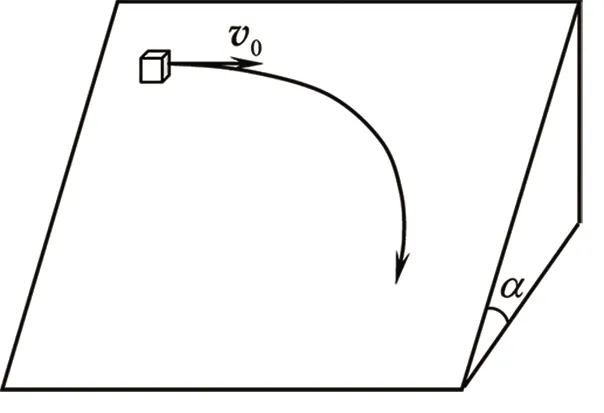
图1 粗糙的斜面上滑块的平抛运动图Figure 1 horizontal throwing motion of slider on rough inclined plane

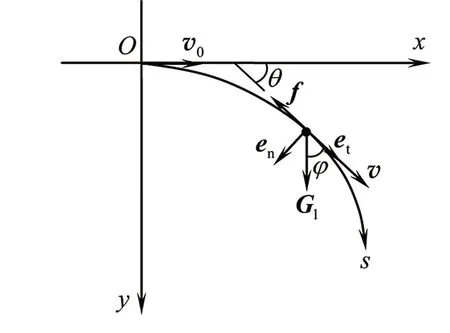
图2 斜面上滑块的受力分析图Figure 2 Force analysis diagram of sliding block on inclined plane

根据受力分析知识知

G1=mgsinα

(1)

f=μmgcosα

(2)

根据力学知识，滑块在图2所示的自然坐标系et-en中的动力学方程为

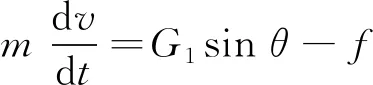
(3)

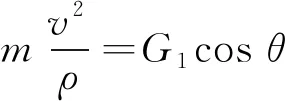
(4)

其中ρ为滑块轨迹的曲率半径，有

(5)

将式(1)、式(2)代入式(3)、式(4)，化简可得

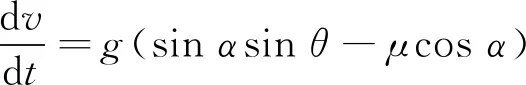
(6)

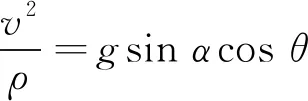
(7)

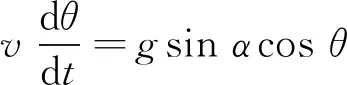
(8)

式(6)除以式(8)即得

(9)

根据初始条件：vt=0=v0和θt=0=0，对式(9)两边进行定积分，可得

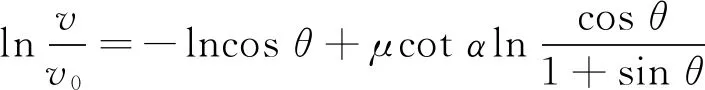
(10)

由于图1中φ=π/2-θ，因此式(10)可以简化成

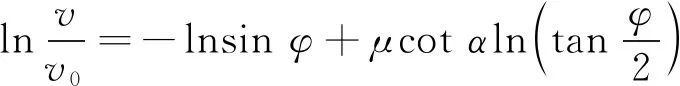
(11)

(12)

则从式(11)可解得

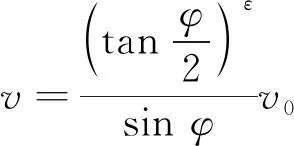
(13)

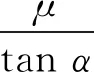
综合式(5)、式(7)、式φ=π/2-θ及式(13)可得

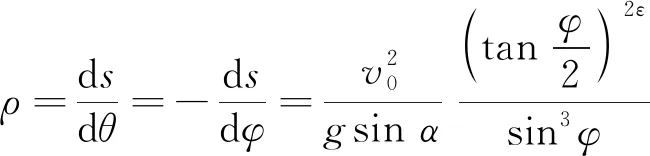
(14)

利用式(14)和式(13)，又可推得

(15)

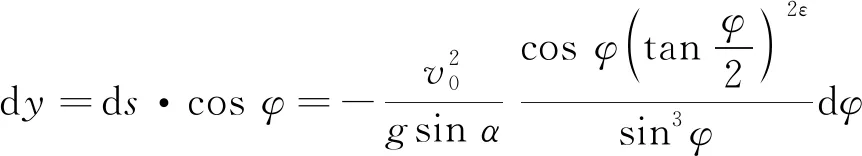
(16)

(17)

可见，在将式(15)—式(17)均积分后，便得滑块的含参轨迹方程和含参运动学方程[2]。

2 关于滑块速率v的讨论

(18)

由此可以判断：

⑵当ε=1时，有

(19)

滑块的速率v同样随φ角的减小而减小。但是当φ=0时有v=v0/2[3,4]，滑块将沿斜面向下做匀速直线运动，此时滑块处于受力平衡状态。

⑶当ε<1时，滑块的速率v将随φ角的减小先减小后增大，最终当φ→0时有v→。经计算，v的极小值vmin出现在

(20)

处，且有

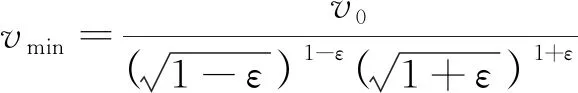
(21)

3 滑块的含参运动学方程及等时逐点运动轨迹

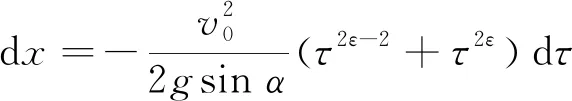
(22)

(23)

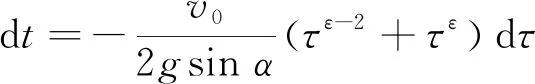
(24)

将式(22)两边积分得

其中积分下限1源自于初始时刻的φ=π/2即τ=1。进一步计算得

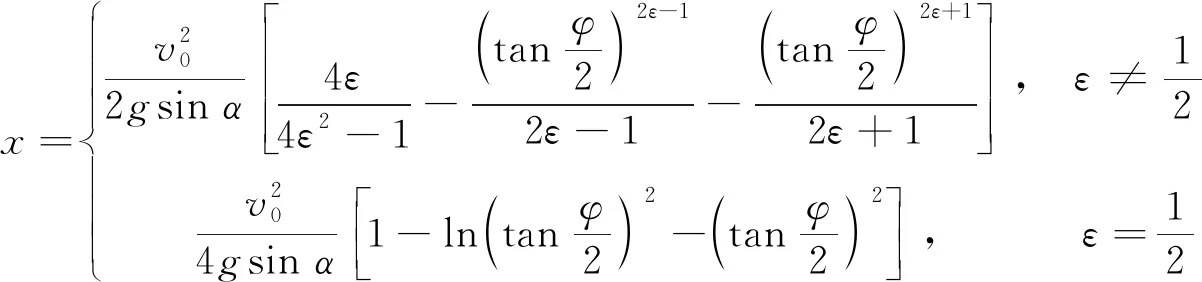
(25)

同理，分别对式(23)、式(24)两边进行相应的定积分，便得

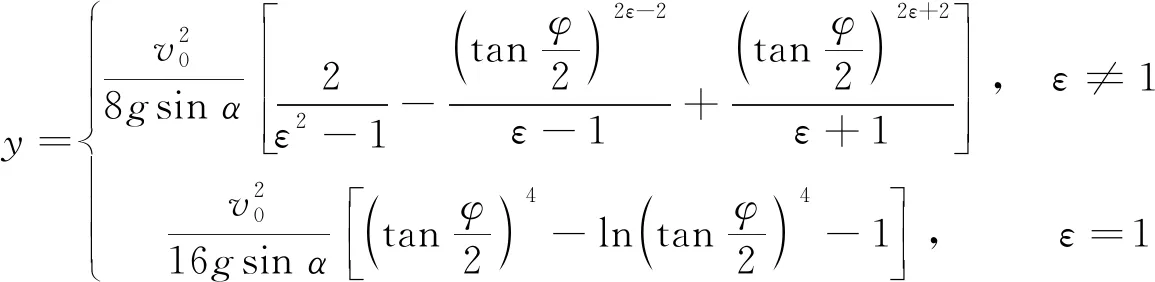
(26)

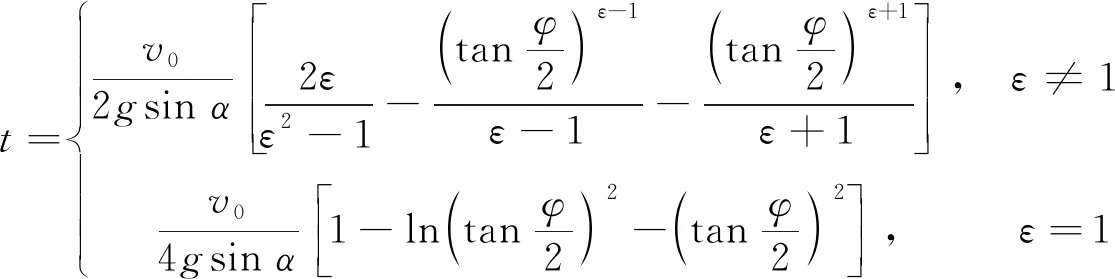
(27)

至此，式(25)—式(27)便构成滑块在粗糙斜面上的含参运动学方程，其中参量为φ角；而式(25)、式(26)则构成滑块的含参轨迹方程。

从式(26)可见，当ε1即斜面的倾角相对较大时，随着φ→0，y→，滑块将沿y轴正方向不断下滑；而当ε>1即斜面相对较平缓时，随着滑块将在y方向停止前进。

图3 大倾角α的斜面上滑块的等时逐点 运动轨迹(Δt = 0.5)Figure 3 Isochronous point by point trajectory of slider on inclined plane with large inclination angle α (Δt = 0.5)

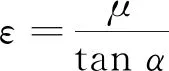
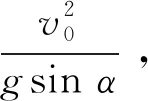
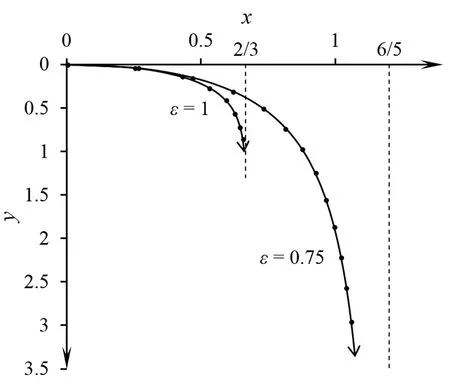
图4 中倾角α的斜面上滑块的等时逐点运动轨迹(Δt = 0.3)Figure 4 Isochronous point by point trajectory of slider on the inclined plane with medium inclination angle α (Δt = 0.3)

图5 小倾角α的斜面上滑块的等时逐点运动轨迹(Δt = 0.1)Figure 5 Isochronous point by point trajectory of slider on inclined plane with small inclination angle α (Δt = 0.1)

4 当0<ε≤1/2时滑块在x方向理论上能够滑至∞远的解释

由于本文所得到的运动学结论均由最初的动力学方程解得，因此对于上述“远”的疑问，只需利用所得到的运动学结论进行分析即可。从运动学的角度讲，滑块在x方向滑动的距离以ε=1/2为分水岭，分为有限和无限的原因，在于位移积分，或者说在于速度分量vx在时间t足够大时趋于0的渐近行为。从滑块的速率表达式(13)可得

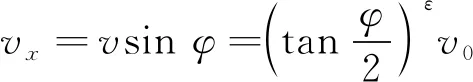
(28)

从式(27)又可得在ε<1的情况下，当φ→0即t→时t的近似表达式：

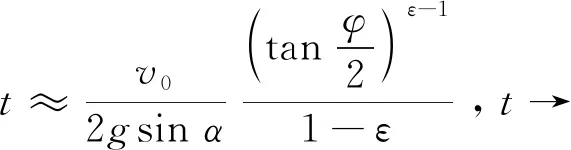
(29)

(30)

可见在t→时，vx随t而趋于0的渐近行为依赖于ε的具体取值。易见，当ε<1/2时，有上述幂函数形式的vx随时间t的衰减速率终将慢于1/t函数，由积分知识知滑块在x方向上的位移。同理，当ε=1/2时，vx随时间t将按1/t函数衰减，滑块在x方向上的位移照样→；而当1/2<ε<1时，vx随t的衰减速率则将快于1/t函数，滑块在x方向上的位移将收敛。

由此可见，虽然滑块在x方向上的速度分量vx随时间t逐渐减小至0，但滑块在x方向上的位移大小Δx却依赖于vx的渐近式(30)，vx→0并不意味着Δx有限！

5 滑块在y方向的运动情况

从滑块的速率表达式(13)又可得

(31)

分析该表达式可知，当ε<1时，vy随φ的减小而不断增大，直至→；当ε=1时，vy也随φ的减小而增大，但当φ→0时vy→v0/2；当ε>1时，vy随φ先增大后减小，直至φ=0时vy=0(注：等号源自运动时间有限)，其间vy的极大值出现在

(32)

处，且有

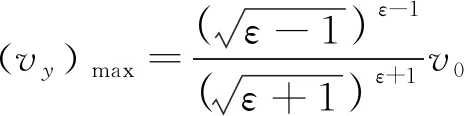
(33)

经与第2节中的v进行对比可以发现，vy随角度φ的变化情况与v有显著的差别。

下面验证：当ε<1时，滑块在y方向上的极限运动(t→)是加速度为g(sinα-μcosα)的匀加速运动。

由式(31)可得，当φ→0即t→时，有

(34)

vy≈gsinα(1-ε)t=g(sinα-μcosα)t

可见滑块在y方向上的极限加速度为g(sinα-μcosα)，符合力学常识。

有必要指出的是，理论上仅当1/2<ε<1时，滑块最终的运动才是严格的沿y轴正方向的匀加速直线运动(见图4)，而当0<ε1/2时，由于滑块在x方向上始终存在着一个缓慢不断趋于0的速度分量vx，参见图3及式(30)，因此滑块在空间最终的运动只能近似地说成是沿y轴正方向的匀加速直线运动！

6 特殊情况下滑块解析形式的轨迹方程与运动方程

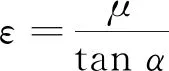
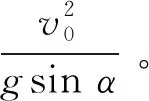
将它和ε=3/2一起代入式(26)，即得此时滑块解析形式的轨迹方程：

(35)

又见式(26)，当2ε+2=2(2ε-2)时，有ε=3，则由式(26)可解得

将它和ε=3一起代入式(25)，即得此时滑块解析形式的轨迹方程：

(36)

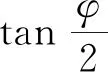
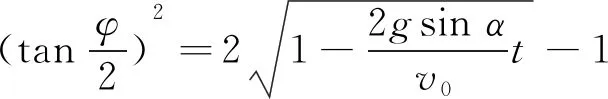
(37)

将式(37)和ε=3一起代入式(25)、式(26)，便得此时滑块解析形式的运动学方程：

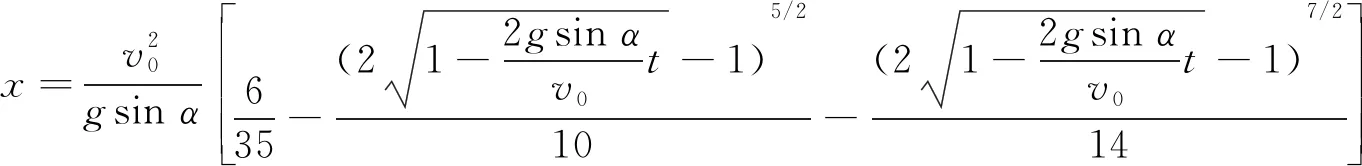
(38)

(39)

注意：这里x、y、t的单位均取1；而将式(37)和ε=3一起代入式(18)，则得

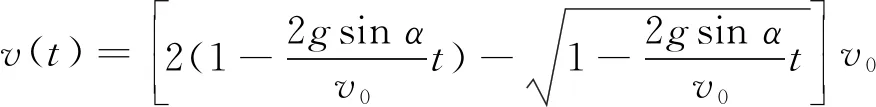
(40)

7 总结与说明

本文的研究丰富和完善了文献[1]对于该问题的讨论，且分析过程更加细致、条理；在给出具体图像的同时，也尝试解释了一些可能存在的疑惑。这些对于大中学物理的教学应具有一定的参考意义。

需要说明的是，虽然文献[7-8]在直角坐标系中利用数学技巧，同样也计算出滑块的含参运动学方程，但是它们的计算过程并不比本文及文献[1]所采用的自然坐标系方法简单，物理图像则更不如本文及文献[1]清晰。