一种低分辨率细胞显微图像的分割与统计

陈书文,曹 愚,赵小燕,王茄吉

(1.江苏第二师范学院 数学与信息技术学院，江苏 南京 210013；2.南京工程学院 信息与通信工程学院，江苏 南京 211167)

细胞数字图像是临床医学、细胞学、病理学的重要研究手段，在疾病诊断、癌细胞筛查中发挥着重要作用。凭借计算机图像分析技术，医生或科研人员能够对目标细胞进行定性或定量分析。这不仅能减少视觉工作量，还极大地提高了工作效率。细胞图像分割是细胞识别与统计的核心，当前分割方法可大致归纳为四类，第一类为阈值法；第二类为基于区域的方法；第三类为基于先验模型的方法；第四类是基于神经网络的方法。

阈值法[1]把每个像素的灰度值作为特征，通过比较灰度值对像素进行分类，一般分为单阈值法和多阈值法[2-3]，具有简单易行、性能稳定等优点[4]。目前流行的阈值法有Otsu法[5]、最大熵法[6]和聚类法[7]等。此类方法对于简单或无噪声的细胞图像表现较好，若遇光照不均匀、染色不均匀、或污染干扰的情况，细胞分割的准确性将受到影响。基于区域的方法不仅要考虑图像的灰度值，还要考虑融合环境。此类方法有区域生长法[8-9]、分水岭法[10-11]等。区域生长法要先确定生长准则，而分水岭法的缺点是容易过分割，这都不能独立地用于分析形状小、密度高的细胞图像。基于先验模型的方法是通过预定的形状来提取特定细胞，再进行分类。但实际问题是细胞形态各异，预先确定细胞模板很困难。而基于神经网络的方法是把图像的分割作为函数的最小化问题来处理，主要思想是用已知的结果作为样本对神经网络进行训练，此方法过程也较复杂。为寻找快速有效、且能应对各种染色污染问题的细胞图像分割法，本文提出基于K-means聚类和Canny算子相结合的新思路，并把新算法的效果与单独使用以上两种方法进行对比，旨在证明新方法的优越性。

1 算法原理

图1 算法流程图Fig.1 Flow diagram of algorithm

给定的细胞图像经过灰度化和中值滤波后，采用K-means聚类作为主分割法，同时用Canny算子的分割结果作为必要补充，把因染色问题导致未被正确检测的细胞统计进来，发挥两种算法的优点，提高细胞识别的准确率(算法流程如图1所示)。要注意的是，若原图像为RGB彩色图像，需先灰度化。预处理时提取图像的RGB三个通道值，选择直方图均衡最好的通道建立灰度图像。一般情况，图像中的细胞核、细胞质、环境背景是3种不同的灰度值，所以首次分割采用的K-means聚类，聚类中心数设置为3。但此分割结果不仅有正常细胞，还包含染色剂污染点，甚至有的浅染色细胞并没有分割出来。第二步，算法使用Canny算子检测细胞边缘，经过孔洞填充和腐蚀，重新确定了一组细胞核的位置坐标。然后对属于同一细胞核、被重复检出的细胞位置进行归并，最终用细胞的特征参数排除染色剂污染点，提高了算法精度。

2 细胞图像的K-means聚类分割

K-means算法是一种动态聚类算法[12]，以欧式距离作为相似度测度，以误差的平方和为聚类准则函数，迭代计算使得准则函数至收敛为止。算法目的是把n个样本点分为k个簇，使簇内具有较高的相似度。算法先随机地选取k个对象作为初始聚类中心(聚类中心代表簇的平均值)，然后对剩余样本根据到各个聚类中心的距离，将它们分配给最近的簇，再重新计算每个簇的平均值。此过程不断迭代直至准则函数J收敛。若进行第m次迭代，需先更新第i个聚类中心zi

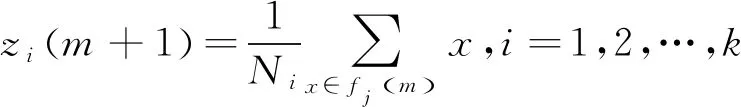
(1)

再计算准则函数

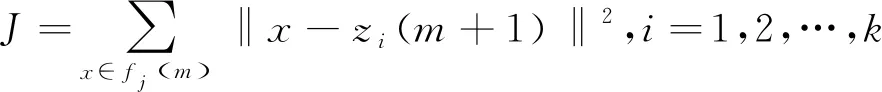
(2)

其中，聚类中心数为k，Ni表示第i个簇的样本数。本文设置聚类中心数为3。原图像灰度化后，其像素被分成了3个簇(即细胞核、细胞质、环境背景)，所以整张图也被分割成了三值图像。提取图像中的细胞核，并用细胞核的质心坐标代表每个细胞的位置，最终得到位置集合S1(I)。此时，S1(I)可能包含染色剂污染点，也可能遗漏染色较浅导致未被分割的细胞核。

3 Canny算子边缘检测分割

Canny算子是基于最优化算法的边缘检测算子[13]。实验证明，Canny算子在处理高斯白噪声污染的图像方面优于其它传统的边缘算子。Canny 算子的实现主要包括四个部分：1)平滑图像；2)计算梯度的幅值和方向；3)梯度方向上对梯度幅值做非极大值抑制；4)双阈值方法检测图像边缘。图像中，每个像素的灰度的梯度值为

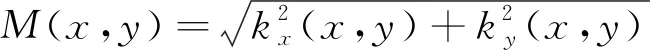
(3)

梯度方向为

H(x,y)=arctan (kx(x,y),ky(x,y))

(4)

其中，kx和ky分别为像素(x,y)的水平梯度和垂直梯度。

Canny算子作用后，图像I生成了关于细胞边缘的二值图像。使用形态学进行孔洞填充和腐蚀去噪，就得到了细胞核的质心坐标。这样，图像I产生了关于细胞位置的集合S2(I)。这里S2(I)包含了未被K-means检出的细胞位置。而属同一细胞核的质心位置一定会被重复检出，需要归并。所以算法需要考查上述二种分割得到位置的并集

S(I)=S1(I)∪S2(I)

(5)

4 结合Canny算子的必要性

(a)原图；(b)K-means；(c)Canny 图2 染色不足的情况举例Fig.2 The case of inadequate dyeing

关于染色问题的一种情况是细胞核染色不足(图2-a)。单独使用K-means聚类处理图像，形成了3个聚类中心，它们一般代表了图像中细胞核、细胞质、环境背景3种区域的灰度平均值。K-means聚类后，算法是根据分离出的细胞核来统计细胞数量，若染色不足(图2-b)，该细胞是不会被统计的。但实践中，即使染色不足导致细胞核灰度接近细胞质，聚类方法失效，也还是能用Canny算子检测出该细胞核的边缘(图2-c)，弥补K-means算法的缺陷。

(a)原图；(b)K-means；(c)Canny 图3 污染块与正常细胞边界模糊举例Fig.3 The fuzzy boundary between the contaminant and normal cell

另一种情况是染色污染块过于靠近正常细胞，两者边界模糊(图3-a)。K-means聚类之后，污染块和细胞核连成一体(图3-b)，导致要识别的细胞核像素面积远超均值，被算法当作大污染块自动排除了，此为统计错误。但由于污染块的颜色常不均匀，Canny算子作用后，污染块不易形成闭合边界(图3-c)，孔洞填充后就不易形成实心点。这样污染块就和正常的细胞分开了，也弥补了K-means算法的缺陷。

如果单独使用Canny算子分割图像，一方面会遗漏没有形成闭合边界的细胞，即对这样的细胞Canny算子是失效的。另一方面，也无法得到细胞核、细胞质的像素面积、周长等量化特征为算法的后续处理做准备。综上所述，Canny算子是K-means聚类的必要补充。

5 染色剂污染点的排除

当染色污染面积远大于细胞的平均值时，可以通过像素面积直接排除；当污染面积与细胞大小相当时，可以综合细胞形状特性参数来排除。第一种情况较为简单，这里不再赘述，主要讨论第二种情况。

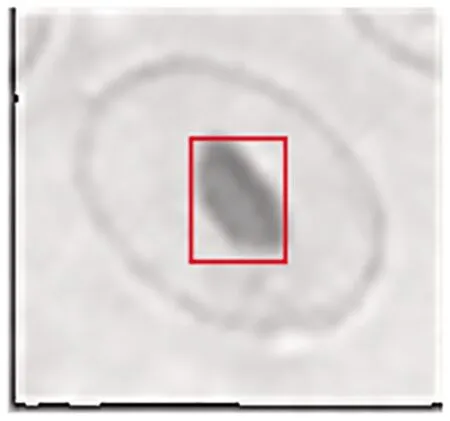
图4 像素计算范围Fig.4 Pixel computing range

6 实验

下面用二例细胞显微图像测试所提出方法的有效性，并把结果与其它算法做了对比，显示新算法的优越性。

6.1 算例1

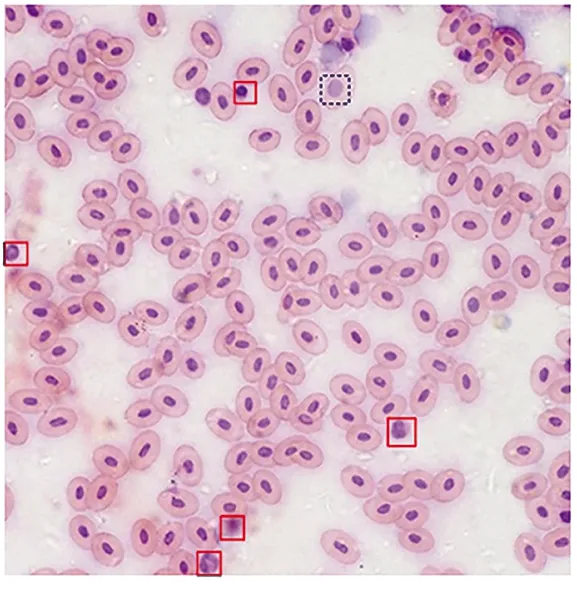
图5 算例1的细胞图像Fig.5 Original cell image of ex.1

图5是一张经过瑞士吉姆萨染色的原细胞图像，其中有浅染色细胞(图5蓝虚线框)和若干染色剂污染点(图5红实线框)。

1)算法的有效性

第一次分割使用聚类中心数为3的K-means法得到三值图像，如图6所示。在图6中提取白色的细胞核，再经孔洞填充和腐蚀去噪，得到二值图像(图7)。图7中发现，K-means分割出了大部分细胞核，但包含了不该包含的染色剂污染点(图7红实线框)，却没包含应该包含的浅染色细胞(图7白虚线框)。

然后使用Canny算子做二次分割获取细胞边缘特征，如图8所示。经孔洞填充(图9)，再腐蚀去噪，由图10计算出细胞核的质心坐标。分割效果令人满意，因为图5中的蓝虚线框所标识的浅染色细胞，在图9或图10的对应地方被Canny算子检测出来了。

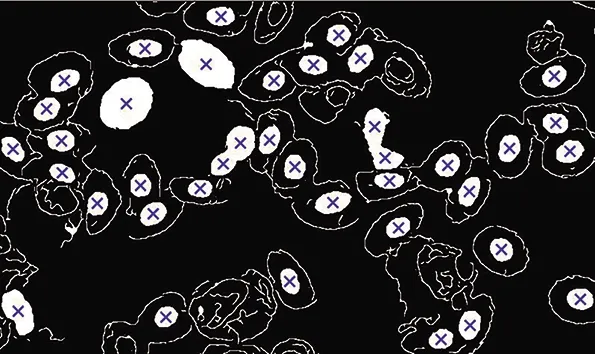
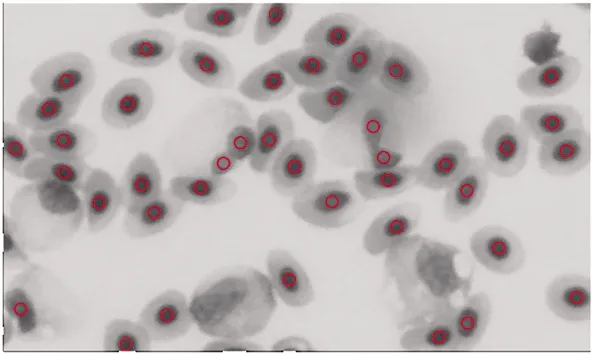
求图7、图10的位置的并集，得到图11。其中红圈表示K-means聚类得到的细胞位置，蓝叉表示Canny算子得到的细胞位置。对属于同一细胞核、被重复检出的细胞质心位置进行归并，并利用细胞核占比、细胞核面积等参数综合筛选出真实的细胞。对于此例，设置细胞核面积阈值为22像素、核占比取值为0.25

图6 K-means分割Fig.6 K-means segmentation

图7 提取细胞核并腐蚀Fig.7 Nuclear extraction and corrosion

图8 Canny算子检测边缘

图9 孔洞填充Fig.9 Hole filling

图10 腐蚀和去噪Fig.10 Corrosion and denoising

图11 合并位置标识Fig.11 Merge position identification

2)与其它方法比较

本文提出的方法与单独使用K-means方法、Canny算子法、脉冲耦合神经网络(PCNN)分割和人工统计的方法对比，统计相对误差如表1所示。K-means方法结果如图7所示，Canny算子法标识如图9所示，PCNN神经网络标识如图13所示。从表1可以看出，本文提出的方法与人工统计相比，相对误差最小(1.1%)，精度达到了98.9%。

图12 合并标识并排除染色剂污染点Fig.12 Eliminate contamination points

图13 PCNN分割后再腐蚀Fig.13 PCNN and corrosion

6.2 算例2

用另一幅经瑞士染色的细胞图像来验证新方法的有效性，如图14所示。其中有浅染色细胞(蓝虚线框)和若干染色剂污染点(红实线框)。

1)算法的有效性

经中值滤波且使用聚类中心为3的K-means法分割，提取细胞核并去噪得到二值图像，如图15所示。与上例不同，本例还需用分水岭法分割粘连细胞(红框中)，得到图16。

表1 不同算法的统计精度Table 1 Statistical accuracy of different algorithms

计算图16中所有细胞核的质心位置，结果标注在图17上。

图14 算例2的细胞图像Fig.14 Original cell image of ex.2

图15 提取细胞核

图16 分割粘连细胞Fig.16 Clustered cells separated

图17 K-means法标注的细胞位置Fig.17 Cell locations labeled by the K-means

以上看出，K-means法标出了大部分细胞核的位置，但也存在着问题。17号点是染色污染点已被K-means排除，而 45和54号染色污染块并没有被K-means排除，这2点为错误统计；另外， 6号点是细胞核(蓝虚线框)，也没能被K-means法识别。原因是K-means无法区分与6号点紧密相连的染色剂污染块(见图16)，导致提取的细胞核面积远超平均值被算法自动排除了。限于篇幅，类似问题不一一叙述。

所以必须借助Canny算子做图像的二次分割，辅助统计。Canny算子获取细胞边缘特征后，经过孔洞填充(图18)、分水岭分割粘连细胞和腐蚀去噪(图19)等步骤获得细胞位置(在图18中用蓝×标注)。将图18结果与图17对比，可以看出原6号位置的细胞在图18中与染色剂污染块分开了；且原54号位置的染色污染块在图18中也被Canny算子自动排除了。

求图17、18的位置的并集，即对属于同一细胞核、被重复检出的细胞质心位置进行归并，并利用细胞核占比、核面积等参数综合筛选细胞，最终得到图20所示结果(统一用红圈标识位置)。从图20看出，新方法排除了染色剂污染的干扰，提高了统计精度。

图18 Canny算子检测Fig.18 Canny operator detection

图19 腐蚀和去噪Fig.19 Corrosion and denoising

图20 合并标识并排除染色剂污染点Fig.20 Eliminate contamination points

2)与其它方法比较

算例2与单独使用K-means方法、Canny算子法、脉冲耦合神经网络(PCNN)分割和人工统计的方法对比，统计相对误差如表2所示。可以看出，本文的方法与人工统计相比，相对误差最小(2.3%)，精度达到了97.7%。

表2 不同算法的统计精度Table 2 Statistical accuracy of different algorithms

7 结论

本文提出了基于K-means聚类与Canny算子相结合方法用于细胞显微图像分割和统计。对于染色程度较浅、或有其它染色污染导致K-means聚类法未能正常识别细胞核的情况，本文采用Canny算子辅助分割以提高统计的准确性。此方法不仅降低了细胞分析中对图像染色质量的要求，还有效地解决了现有细胞统计方法的误差较大的问题。