一类随机反应扩散方程的快速扩散极限

雷 婷,陈光淦

(四川师范大学 数学科学学院&可视化计算与虚拟现实四川省重点实验室,四川 成都 610068)

反应扩散方程在动力学上的主要特征一方面是物质在相互转化下局部化学反应的影响[1],另一方面是物质在空间中扩散。反应扩散方程因其广泛的实际应用背景而被众多数学家关注[2-5]。

本文研究下列Hilbert空间H中带加性噪声的随机反应扩散方程

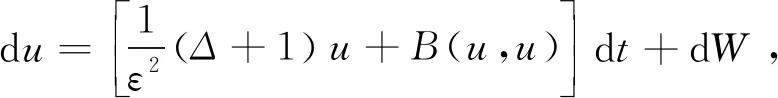
(1)

其中随机过程u=u(t,x):[0,T]×[0,π]→,有界算子B和有限维的Wiener过程W在第1节将给出详细定义。本文的主要目的是严格建立方程(1)在快速扩散的极限条件下的有效近似。

用类似于Flandoli[6]的方法,在下节的基本假设下,易知方程(1)的Cauchy问题存在唯一的局部解。本文主要证明了方程(1)的解可由方程

u(t)=b(t)+Z(t)+error

有效近似,其中Ornstein-Uhlenbeck过程Z(t,x)将在定义1.2中给出。

db(t)=2Bc(b,Z)+Bc(Z,Z)+dWc,

其中Wc=PcW,Bc=PcB,Pc是投射到核空间N的算子[7],详细定义将在第一节给出。

本文的结构如下,在第1节,给出了随机反应扩散方程的相关定义和假设。在第2节,给出文章的主要结论。在第3节,证明了主要结论。

1 预备知识

设Hilbert空间H的内积和范数可分别表示为〈·,·〉和‖·‖。记算子A=△+1,则A满足Aek=-λkek,其中λk满足0λ1λ2…λk…,并且对所有足够大的k,有λk≥Ckm成立。是H中的标准正交基。

令N:=kerA,T:N⊥在N空间H的正交补集,并且Pc:H→N。Ps:=I-Pc。Pc和Ps与算子A可交换。假设N的维数为n,其对应基为{e1,…,ek}。

定义1.1[8]对任意的α∈,定义空间Hα为

进一步算子A生成的解析半群{etA}t≥0为

并且存在常数M>0和K>0,对任意的t>0,βα和任意的u∈Hβ,满足

‖etAPsu‖α

(2)

假设1.1设α,β是公式(2)中的参数,B是从Hα×Hα到Hα-β的有界双线性映射,有B(u,v)=B(v,u)=u·v成立,并且对任意的u∈N,满足PcB(u,u)=0。简记符号Bs=PsB,Bc=PcB,其中PsPc如上定义的投射算子。

假设1.2W为H空间上的Wiener过程,假设当t>0,

其中βk(t)是上独立的标准Brownian 运动,ρk为实数,N是某个正整数。

注记1.1若控制无穷级数收敛,则当N=时,假设1.3也成立。例如:W的有界协方差算子为其中{αk}k是一组有界实序列,{fk}k∈是H空间上的一组正交基。假设

因此为了简单起见,取假设1.2中的N<。

定义1.2定义O-U过程Z(t)为

其中

定义1.4对于随机过程{Xε(t)}t≥0,若对任意的p≥1,存在常数Cp,满足

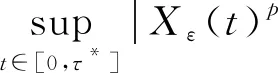
C

p

f

ε

,

本文除特别说明外,C表示所有正的常数。

2 近似理论

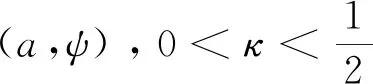
将方程(1)的解u分解为

u(t)=a(t)+ψ(t),

(3)

其中a∈N,ψ∈N⊥。将u=a+ψ带入到方程(1)中, 可得

da=[2Bc(a,ψ)+Bc(ψ,ψ)]dt+dWc，

(4)

和dψ=[ε-2Asψ+Bs(a,a)+2Bs(a,ψ)+Bs(ψ,ψ)]dt+dWs。

(5)

方程(5)的温和解为

(6)

其中Z(t)在定义1.2中被定义。在第一步逼近中,ψ近似于O-U过程 (引理3.1中有严格的证明过程)。因此,用Z替换公式(4)中的ψ,得到

da≈[2Bc(a,Z)+Bc(Z,Z)]dt+dWc。

令b:[0,T0]→N是方程

db=[2Bc(b,Z)+Bc(Z,Z)]dt+dWc

(7)

的解。

下面给出本文的主要结论：

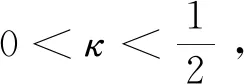
其中

Q(t)=Z(t)+eε-2tAsψ(0)。

3 定理2.1的证明

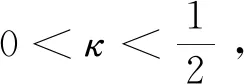
‖ψ(t)-eε-2tAsψ(0)-Z(t)‖αCε2-2κ。

证明由公式(6),利用三角不等式和半群估计

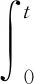
其中运用公式(2),引理3.1得证。C>0

引理3.2[8]在定义1.1和假设1.2的条件下,存在常数,αk,λk,κ0>0和T0,满

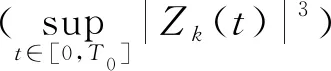
Cε

,

Cε

,

其中Zk(t)和Z(t)在定义1.2中被给出。

引理3.3在引理3.1,3.2条件下,若ψ(0)=O(1),则存在常数C>0,满足

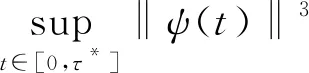
C

。

证明利用引理3.1,3.2和三角不等式,由公式(6)得到

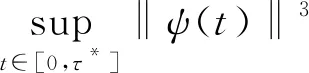
Cε

6-6κ

+

C

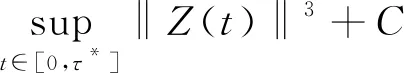
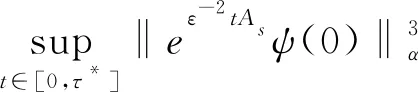
完成引理3.3的证明。

引理3.4在定义1.2和假设1.1,1.2的条件下,定义随机过程b(t),其初始条件‖b(0)‖C,

(8)

那么对于T0>0, 存在常数C>0, 满足

C

。

证明为了验证b(t)有界,定义X为

X(t)=b(t)-Wc(t)。

(9)

将公式(9)代入到公式(7)中, 得到

∂tX(t)=2Bc(X+Wc,Z)+Bc(Z,Z)。

在公式等号两边同做内积,则

再利用Cauchy-Schwarz不等式和Young不等式,可得

∂t‖X‖2C[1+‖Z‖2]‖X‖2+C‖Z‖2[‖Z‖2+‖Wc‖2]。

由引理3.2,

∂t‖X‖2

利用Grownwall引理,当ε充分小时,

‖X‖2

结合公式(9),得到

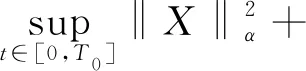
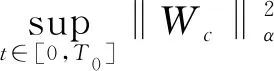
C

。

引理3.5存在常数C>0,满足

证明利用公式(2)得到

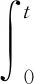
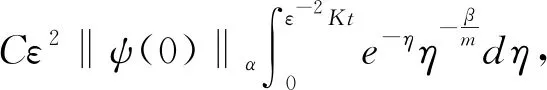
结论得证。

引理3.6若假设1.1,1.2成立,则

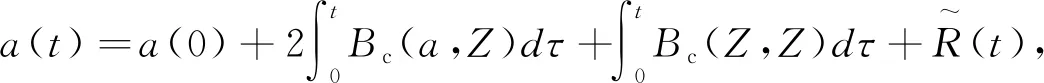
(10)

证明由公式(6)和引理3.1,得到

ψ(t)=eε-2tAsψ(0)+O(ε2-2κ)+Z(t)。

(11)

记

y(t)=eε-2tAsψ(0)，R(t)=O(ε2-2κ)。

将公式(11)代入到公式(4)中,得到

对Bc运用[9]的方法上,从而得到

其中

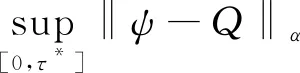
引理3.7集合Ω*的概率近似于1,因为

运用Chebychev不等式和引理3.1,3.2,3.4,3.6,得到

引理3.8在定义1.2和假设1.1,1.2的条件下,b为方程(9)的解,a在空间Ω*上由公式(5)定义,且‖a(0)‖C。如果初始条件满足a(0)=b(0),那么在空间Ω*上,对于0κ满足

(12)

和

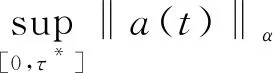
(13)

证明定义

h(t):=a(t)-b(t),

由公式(10)得

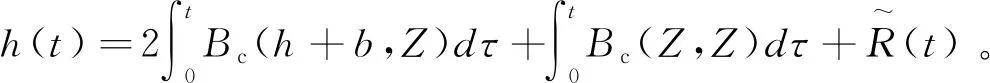
(14)

定义

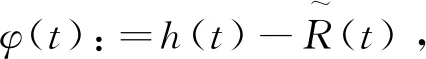
由公式(14)得

(15)

在公式(15)等号两边同做内积,得到

运用Young不等式和Cauchy-Schwartz不等式,有

利用定义3.1,得到

运用Gronwall不等式,有

因此,在空间Ω*上

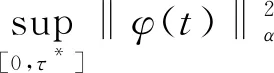
(16)

考虑运用公式(16)和定义3.1,得到

公式(12)获证。进一步

运用公式(12)和定义3.1,得到(13)。

定理2.1的证明

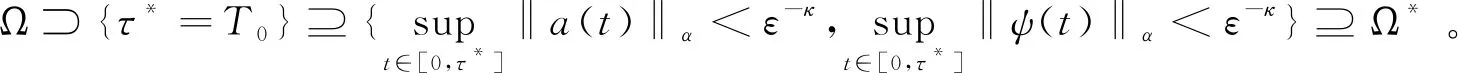
对于近似结论,运用公式(13)和三角不等式,得到

因此,