Littlewood-Paley算子的变指数交换子在变指数空间上的有界性

房成龙,张 婧

(伊犁师范大学 数学与统计学院,新疆 伊宁 835000)

引 言

二十世纪三十年代,Littlewood和Paley在文献[1-3]中讨论Fourier级数的二进分解问题时,首次引入了下面一维的g函数定义,

对于Fourier级数的分解,函数g的研究是一个基础,Littlewood和Paley证明了

‖g(f)‖p≈‖f‖p

(1)

基于上面一维理论,Stein运用Poisson积分给出了n维的Littlewood-Paley g函数定义,并验证了(1)依然成立。之后,许多学者对n 维Littlewood-Paley算子产生了浓厚的兴趣。

1989年,王[4]介绍了比Poisson核更弱的核ψt，对应定义了更一般的n维Littlewood-Paley g函数:若ε>0,ψ是满足下面性质的一个固定函数；

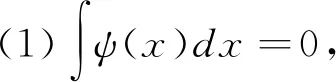
(2)|ψ(x)|C(1+|x|-(n+ε)),

(3)|ψ(x+y)-ψ(x)|C|y|ε(1+|x|-(n+1+ε)),当2|y|<|x|;

则Littlewood-Paley g函数定义为

其中Ft(f)=ψt*f,ψt(x)=t-nψ(x/t),t>0。

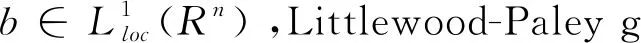
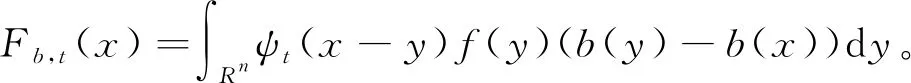
2005年，张和刘[5]验证了gψ,b在加权Lebesgue空间上的有界性。2009年,薛和丁[6]获得了gψ,b在端点处的加权估计。

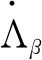
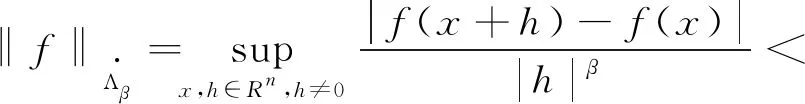
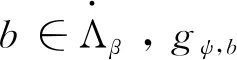
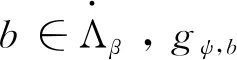
另一方面,2010年,范[9]给出了下面形式的变指数Lipschitz空间定义：

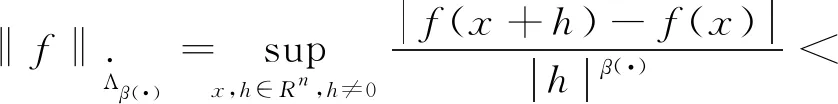
并获得了变指数Lipschitz空间的一个重要刻画,

2018年,郭,周和房[10]运用范[9]的结果证明了一些算子的变指数Lipschitz交换子在变指数Lebesgue空间上有界性。

受上面研究启发,本文作者产生一个疑问:Littlewood-Paley算子的变指数Lipschitz交换子在变指数空间上是否有界? 文章第二部分给出了肯定回答。下面将介绍变指标空间有关的概念。

为了方便,我们给出本文中的一些基本记号,Rn表示n-维实欧几里得空间,C为一般的非负常数。若存在常数C1,C2>0,使得AC1B且BC2A,则A≈B。

1 定义和引理

将所有p:Rn→[1,)且满足

的可测函数组成的集合定义为Ρ(Rn)。

另外,将所有p:Rn→(0,)且满足

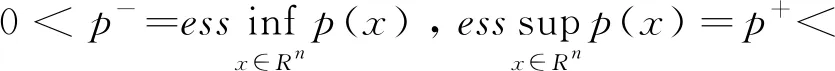
的可测函数组成的集合定义为Ρ0(Rn)。

引理1(见[9]) 若β(·)∈Ρ0(Rn),q(·)∈Ρ(Rn),则

这个结果的具体证明可见文献[9,p4159]和文献[11]。值得注意的是,若Q*⊂Q,有

|fQ*-fQ|

对于一个连续函数g,若存在clog>0使得对所有的x,y∈Rn,满足

|g(x)-g(y)|

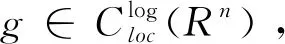
|g(x)-g|

则称g是全局log-HÖlder连续的,简记为g∈Clog(Rn)。其中g

定义2若p:Rn→(0,)是可测函数,Lp(·)(Rn)空间表示下面函数的集合,

其范数定义如下:

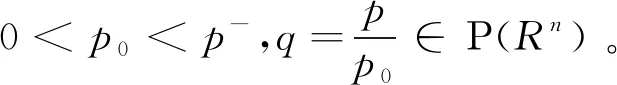
在讨论Littlewood-Paley算子交换子的有界性时,要借助于极大算子,下面给出与极大算子相关的一些结果。

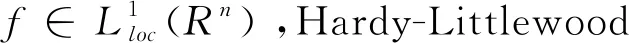
记Β(Rn)为所有满足p∈Ρ(Rn)且Hardy-Littlewood极大算子在Lp(·)(Rn)上有界的函数组成的集合。同时,变指数分数次极大算子Μα(·)定义如下:

定义4(见[12]) 变指数Riesz位势算子Iα(·)定义如下:

变指数分数次极大算子与变指数Riesz位势算子具有下面关系

Μβ(·)f(x)CIβ(·)(|f|)(x),

证明见[9,p11],而变指数Riesz位势算子在变指数Lebesgue空间上有界(见[12]),故有下面引理。

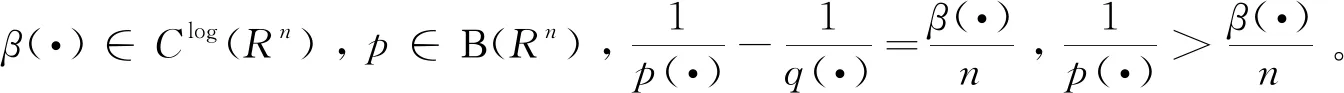
则

‖Μβ(·)(f)‖Lq(·)C‖f‖Lp(·)。

2 主要定理

则对每个固定的x∈Rn,Ft(f)(x)可以看作是一个从[0,)到H的映射,明显的

gψ(f)(x)=‖Ft(x)‖,gψ,b(f)(x)=‖Ft(bf)(x)-b(x)Ft(f)(x)‖。

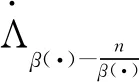
证:假设Q=Q(x0,l),suppf⊂(2Q)c。明显的,当x∈Q,y∈(2Q)c时,可得

|x0-y|≈|x-y|。

首先,根据引理1可得,

‖Ft(f(b-bQ))(x)-Ft(f(b-bQ))(x0)‖

运用上面估计,分别去证明(a)和(b)。

(a)明显的

Ft(bf)(y)-b(x)Ft(f)(y)=Ft((b-bQ)fχ2Q)(y)+Ft((b-bQ)fχ(2Q)c)(y)-(b-bQ)Ft(f)(y)。

则运用前面估计即有

|gψ,bf(y)-gψ((b-bQ)fχ(2Q)c)(x0)|

=‖Ft(bf)(y)-b(y)Ft(f)(y)‖-‖Ft((b-bQ)fχ(2Q)cx0)‖

=‖(b-bQ)Ft(f)(y)‖+‖Ft((b-bQ))fχ2Q(y)‖+‖Ft((b-bQ))fχ(2Q)c(y)

+Ft((b-bQ))fχ(2Q)c(x0)‖。

故

=I+II+III。

首先,由引理1得

I

II

最后,估计III,明显地,运用gψ的有界性得III

(b)运用前面(a)的估计,可得

因此,运用引理2,有

‖gψ,bf‖Lq(·)

故定理得证。