装甲装备观瞄系统状态评估的方法研究
杨延超,李英顺,李 茂,贺 喆
(1.广西科技大学 电气与信息工程学院,广西 柳州 545000;2.大连理工大学 控制科学与工程学院,辽宁 大连 116200;3.陆军驻沈阳地区第三军事代表室,辽宁 沈阳 110000)
针对装甲装备智能化、模块化、集成化、数字化程度高,各部件机理复杂,关联性强,出现故障时无法及时有效地判断故障位置和故障原因,设计专门故障诊断与健康管理系统十分必要[1],而状态评估作为故障排查与故障检修的必要前提也越来越被人们所重视。装甲装备中的观瞄系统构造机理极为复杂,由瞄准镜控制盒、瞄准镜、陀螺仪组、驱动电机等部分组成[2],在众多指标中存在大量定性指标和定量指标,不能使用常规数据分析方法对信号数据进行处理;另一方面,由于整个火控系统是一个闭环结构,多数信号相互叠加,评估指标之间的相互关联直接导致各指标状态等级之间存在着模糊不确定的关系,由此看出仅仅分析独立信号很难对观瞄系统整体状态得出结论,在状态评估方面宜采用多指标综合分析系统。
层次分析法不仅仅是单纯的数学方法,更多的是将行为、逻辑、推理等定性的方法与定量方法有机地结合起来,使得思维过程数学化和系统化,它可以处理许多传统的最优化技术无法着手的实际问题,尽管所需要的定量数据较少,但是对于问题的本质以及内在因素的分析极为清晰[3]。文献[4]中电缆绝缘寿命评估健康指标包含定性、定量指标,针对定性、定量指标统一标准化问题,提出基于模糊层次分析法的寿命评估模型;但是层次分析求权重通常较为主观,例如文献[5]中采用的是评估专家打分制,利用专家经验构建样本矩阵,结果往往不具有客观性;文献[6]针对层次分析主观性较强的问题,采用三标度法取代九标度法,降低了人的主观性对评价结果的影响。在实际工程中常常面对复杂决策的不确定性问题,文献[7]提出了利用灰色理论方法对指标进行灰色分类构建多标准决策分析方法,重点研究指标之间的相互作用问题;文献[8]则对灰色聚类进行了改进,使用了修正模型-指数型白化权函数,解决不同灰类等级指标之间零权重的问题,避免出现当两个指标量数值差异较大时被省略掉的有价值信息从而影响评估结果,为后续评估工作提供客观条件。
纵观已有文献,对观瞄系统状态评估的研究尚未深入,观瞄系统是一个结构复杂、信号繁多的控制系统,针对信号相互叠加和定性、定量指标相结合的特点,采用灰色聚类融合层次分析法建立评估模型,将定量指标、定性指标有效结合,并充分分析指标之间相互作用的影响,提高评估的客观性、科学性和准确性。
1 层次分析法
1.1 基本原理
层次分析法是将多种影响因素进行层次化分解,并逐层比较分析其相关性,主要是对研究对象的评估和对事物发展的预测提供依据。面对一个复杂系统,层次分析法首先会对其包含的各种影响因素进行分析,并将这些因素按照一定逻辑顺序进行分类,以构建层次有序的等级结构;其次按照分组的不同,对其分组内部的各影响因素进行相对重要性的比较,建立判断矩阵;通过一系列公式计算求得该矩阵的特征值和特征向量,得到下一层次各要素对上一层次某要素的重要性次序,从而建立相应的权重向量和权重矩阵,具体流程如图1所示。

1.2 改进的层次分析法
通过查阅文献[9-10],从1-9标度和9/9-9/1标度的层次分析法的计算步骤中可以看出,传统方法主要基于专家经验的分析判断,难以避免人为因素对分析结果的影响;某些因素难以两两比较,往往导致结果的不合理性。针对以上问题,笔者对层次分析法进行改进,改进的层次分析法在两个方面进行了调整,首先使用三标度法代替九标度法,降低人的主观性对评价结果的影响;其次采用最优传递函数构造判断矩阵和拟优一致矩阵,通过计算拟优一致矩阵特征值可以直接求得权重,在这个过程中省略了一致性检验的步骤,简化计算过程提高评估效率。具体计算步骤如下:
1)求出比较矩阵:
(1)
式中:A是以检测值aij为元素的初始样本矩阵;aij为第i(i=1,2,…,m)个对象关于第j(j=1,2,…,n)个指标的检测值。
2)求出第i个对象与所有指标比较结果并分别求和得到排序指数:
(2)
3)根据排序指数ri构造判断矩阵B,其元素bij为
(3)
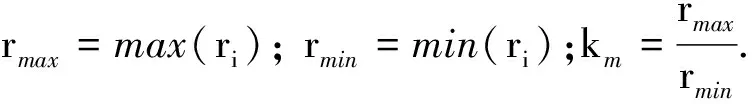

(4)
Cik=lgbik.
(5)
5)求出拟优一致矩阵B′的特征值w11,首先按列归一化B′矩阵,得到矩阵T,其各元素为
(6)
求取T矩阵特征值w11(即指标权重):
(7)
重复步骤1到5,求出其他准则的权重值w12、w13、w14、…,以及准则层对于目标层的权重w1、w2、w3.
2 白化权函数的建立
2.1 传统白化权函数
常见的白化权函数多采用降半梯形结构,不同级别灰类的白化权函数只与其相邻的两个级别灰类存在相互关联的情况,但是当灰类级别之间的指标量数值差异较大时,在中间就会省略掉许多有价值的信息,因此笔者采用灰色白化权函数的修正模型-指数白化权函数[8],指数白化权函数可以有效解决指标在不同灰类等级之间零权重的问题。
指数白化权函数模型如图2所示。

对应图2的(a)、(b)、(c)数学表达式,分别为
(8)
(9)
(10)
2.2 利用FCM聚类计算转折阈值
白化权函数转折点的值称为阈值,通过查阅文献发现传统计算白化权函数阈值主要由相对阈值[11]和平均值法[10]两种获取方式,但是这两种选取方式较为主观,比较依赖于样本矩阵的最终结果。笔者使用一种新的选取方式,使用FCM聚类计算阈值。
笔者利用改进的FCM聚类算法求取聚类中心,详细计算过程参考文献[12]。根据FCM聚类算法得到C个类别,结合灰色聚类的知识体系,将聚类中心带入到式(11)确定相应各白化权函数的阈值,进而得到观瞄系统各指标标准状态的灰色聚类系数。
(11)

2.3 灰色评估系数
对于评估指标Aij,其属于第e个评估灰类的灰色评估系数记为ηije,则有
(12)
对于评估指标Aij,其属于各个评估灰类的灰色评估系数记为ηij,则有
(13)
2.4 权向量及权矩阵
第i组对象第j个评估指标Aij属于第e个灰类等级的灰色评估权记为rije,则有
(14)
通过式(14)得到评估指标Ai所属指标Aij对应各个评估灰类权组成的灰色评估权矩阵R,则有:
(15)
灰色评估权向量ri由评估指标Ai对所属指标Aij的权重集Wi=(wi1,wi2,…,wij)与灰色评估权矩阵的乘积得到,则有
ri=Wi·R=

(16)
3 实例分析
3.1 评估样本数据采集整理
装甲装备的火控系统是一个闭环结构,而观瞄系统作为其中的重要环节承担着信号传输、信号反馈和信号调节的作用,所以观瞄系统的输入输出信号多达几十个,且其中许多信号与其他设备信号相互叠加综合作用。受篇幅限制只选取某型装甲装备观瞄系统上反射镜力矩电机为评估对象,对稳像工况和装表工况条件下上反射镜碰框时力矩电机的运行状况进行评估。选取一台已知状态的武器装甲观瞄系统的上反射镜力矩电机,分别在两种工况条件的同等环境下分别测得5组数据,检测其运行状况与实际运行状况相比较是否相同,以验证本文改进的算法的有效性。首先通过层次分析将能够反映上反射镜碰框时力矩电机运行状况的典型指标进行层次分解,分别得到一级故障源和二级故障源,典型指标如表1所示。

表1 典型指标
具体层次分解图如图3所示。

对于定量指标,需要对4个电源模块进行数据采集。通过在某装甲维修厂的实车采集可得到上反射镜力矩电机运行的监测数据,由于本实例是动态评估,所以对上反射镜力矩电机进行有条件多组采样,分别在装表工况和稳像工况条件下分别采集5组数据,具体定量数据如表2所示。
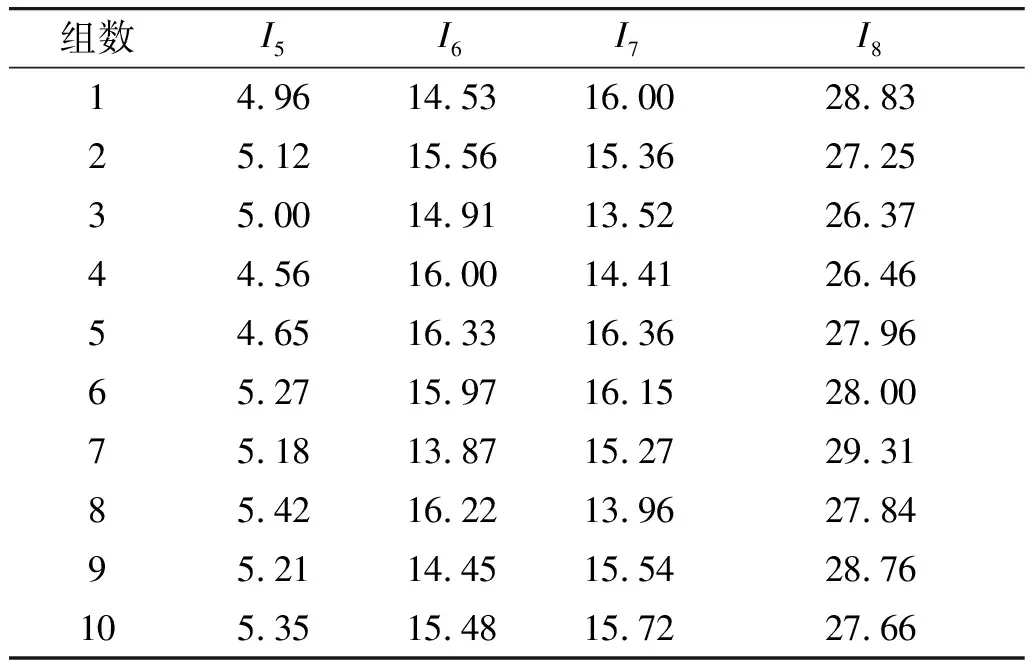
表2 上反射镜碰框时力矩电机运行定量试验数据
因不同指标的量纲与数量级存在差异,导致数据较难统一计算,故需对各指标量进行归一化处理。对于定量指标(即I5、I6、I7、I8)类的指标量,通过规范化式(17)进行归一化:
(17)
使试验数据处于[0,1]区间内,其中最大、最小值如表3所示。

表3 定量指标最大最小值范围
对于定性指标(即I1、I2、I3、I4、I9、I10、I11、I12)类的指标量,根据查询某装甲维修厂观瞄系统上反射镜力矩电机的近两年的历史维修记录,并结合参考某型号装甲装备观瞄系统技术勤务手册,对常见故障进行整理分类,分别求出近两年每种故障源的发生概率。
观瞄系统是典型的电子设备,电子设备由于种类的不同,其质量与可靠性也不同,需要将电子设备的可靠性预计考虑在内,本文中使用GJB/Z 299A—1991电子设备可靠性预计手册分别计算元器件失效率预计[13],根据电子设备的可靠性预计及其使用年限相比较,适当将临界电子设备考虑到潜在故障源,并计算出近两年内电子设备发生故障的概率,具体定性指标描述如表4所示。定量指标归一化及定性指标故障源发生概率如表5所示。

表5 实验测试数据
3.2 评估指标权重确定
在确定评估指标体系后对指标进行权重分析,使用前文中改进的层次分析法对指标进行赋权,首先利用三标度法求出比较矩阵,根据比较矩阵求出的排序指数构造拟优一致矩阵,最后通过计算拟优一致矩阵的特征值获取各指标权重,由于受篇幅影响,此步骤直接给出最后的一级故障权重矩阵和二级故障权重矩阵w1和w2:
w1=[0.170 0.670 0.170],
3.3 FCM求取灰类阈值
将表5中的实验数据带入到FCM聚类算法流程中,通过文献[12]计算流程分别求出初始聚类中心、距离矩阵d(xi,xj)和划分矩阵U(b),最后根据式(10)获取各个指标的白化权函数的灰类转折阈值,具体阈值矩阵为

3.4 指数型白化函数模型的建立




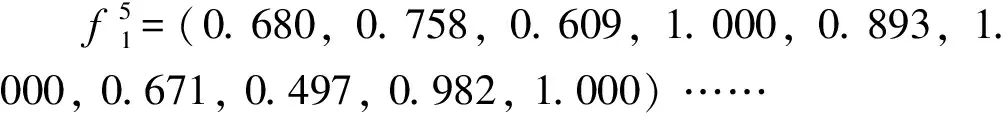
3.5 灰色评估
根据前文所述的方法,以上反射镜碰框时力矩电机为例计算各指标灰类的评估系数及评估权向量,将白化权函数值带入到式(12)~(15)得到灰色评估权矩阵:

根据最大隶属度原则,上反射镜碰框时力矩电机运行时各指标状态等级如表6所示。

表6 上反射镜碰框时力矩电机运行时各指标状态等级
3.6 综合评估
综合状态评估是对评估对象的整体情况进行全面评估,获得其整体运行情况,根据一级故障权重w1和评估权向量R的乘积得到最终评估值r.
由于计算得出的评估结果r是一个向量,它只能够反映研究对象评估结果属于各灰类的程度,并不能反映出对象的综合评估结果,故对r进行单值化处理,引入新的向量符号CT,使用评估灰类等级为其赋值:CT=[0.363 5 0.507 3 0.602 8 0.710 8 0.796 8]T,故R=r×CT=0.628 0,综合评估值r=0.628接近阈值0.603,故判定该上反射镜碰框时力矩电机运行状态为一般。笔者计算得到的结果与实际参与实验的上反镜力矩电机状态一致,故方法准确有效。
3.7 算法评估对比
再取10台同等型号装甲装备的观瞄系统上反射镜力矩电机,分别在稳像工况和装表工况条件下测得10组数据,采用本文改进后的方法和传统的方法如文献[9]和[11]分别对10台上反镜力矩电机进行综合评估,具体评估结果如图4所示。

从图4可知改进前的算法和改进后的算法分别产生了不同的状态结果,其中第5、6、8、9组评估结果发生了跳变。评估结果不同的主要原因是传统的灰色白化权函数多采用的是降半梯形结构,忽略了不相邻指标之间的关联性,导致部分有效信息的缺失;传统的九标度层次分析法无法避免人为因素对权重结果的影响,不具有客观性。多种原因导致了传统算法评估结果的偏差,从而验证了改进的灰色理论融合层次分析法所建立的模型是合理并且科学有效的。
4 结束语
针对信号繁多复杂的观瞄控制系统,所提方法相比较其他传统状态评估方法更加符合实际应用。采用层次分析法可以将定性指标和定量指标有效结合起来,并且改进后的层次分析法可以客观确定指标权重;将模糊聚类与指数型白化权函数相结合,充分考虑不相邻指标之间的关系,解决灰色聚类算法中不相邻指标之间零权重的现象,避免漏掉有价值信息,使得评估结果更加科学、客观,为维护人员提供了维修建议,也为后续设备的故障诊断和健康管理提供了理论基础,具有实际意义。此方法适用于任意具有定性、定量指标的系统对象,具有普遍性。

