基于故障树分析的弹载固态存储器可靠性研究

胡时光，尤文斌，丁永红，路万里，王海霞

(中北大学 电子测试技术国家重点实验室，山西 太原 030051)

随着导弹技术的发展，固态存储器在其研发过程中的地位愈发重要，其可靠性直接决定了所测的飞控数据是否准确有效，关系着导弹的后期设计改进研发。因其具有发射回收负载高、一次使用及长期贮存的特点[1]，使得在可靠性方面存在诸多问题，可能会导致数据存储失败，如何可靠地获取数据一直是固态存储器的研究重点[2]。通常研制部门基于经验预估判断固态存储器可靠性，缺乏定性定量分析描述系统的失效机理和失效模式，在系统故障时难以及时找出故障位置，未能形成有效的可靠性研究。

针对以上问题，笔者提出了基于故障树分析的固态存储器可靠性研究。通过研究固态存储器的组成和测试原理，建立固态存储器的故障树模型，定性定量分析研究固态存储器的可靠性，阐明系统的逻辑关系，对各底事件进行重要度排序，有助于研发人员及时定位故障位置，为今后的固态存储器研发改进提供参考。

1 故障可能性分析

在测试过程中，固态存储器位于弹体内部，需进行回收，要经过发射、飞行以及跌落3个过程，发射与跌落过程属于瞬态高冲击、强振动过程。在此过程中，固态存储器会受到极大的加速度冲击，在此恶劣工作环境下经常会导致固态存储器的关键部件失效，这将会对新型武器的研制改进造成难以估量的损失。

固态存储器主要组成有机械壳体和存储记录电路，在高过载条件下常见失效形式主要分两类：一是机械壳体变形；二是存储记录电路失效。在跌落回收过程中固态存储器受高g值冲击载荷[3]，可能导致机械壳体变形压缩内部空间致使内部电路失效；或直接导致内部电路构件松动、断裂等情况失效。因此固态存储器可靠性研究重点在于存储记录电路。

以某型号弹载固态存储器为例进行分析，其内部存储记录电路实物图如图1所示。主要由模拟采编模块1、模拟采编模块2、数字采编模块、电源调节模块以及存储控制模块5个部分组成。

存储记录电路主要完成多路模拟信号的采集调理、编码及存储；完成PCM数字量的采集、串并转换及存储；完成外部输入电源的隔离转换；完成记录数据的发送和接收单元测试台的控制命令。 从底层元器件出发对存储记录电路进行剖析，电路各模块是由电阻与电容、连接导线、集成电路、接插件、印制板与焊点、半导体分立器件等组成。集成电路又包括模拟电路、模拟开关、A/D变换器、数字电路、Flash存储。半导体分立器件又包括二极管和光耦。存储记录电路框图如图2所示。

鉴于模块分析的冗余性和复杂性，以及保证测试数据的完整性，根据固态存储器电路系统组成和测试原理，按照部件种类划分可靠性预计单元，把不同模块间的相同器件进行归类合并，分析研究其各类元器件的主要失效模式和失效机理，依据单元在电路系统上的功能，采用元器件应力分析法，建立形成典型失效案例[4]。可靠性框图如图3所示。

2 相关理论

2.1 可靠性知识

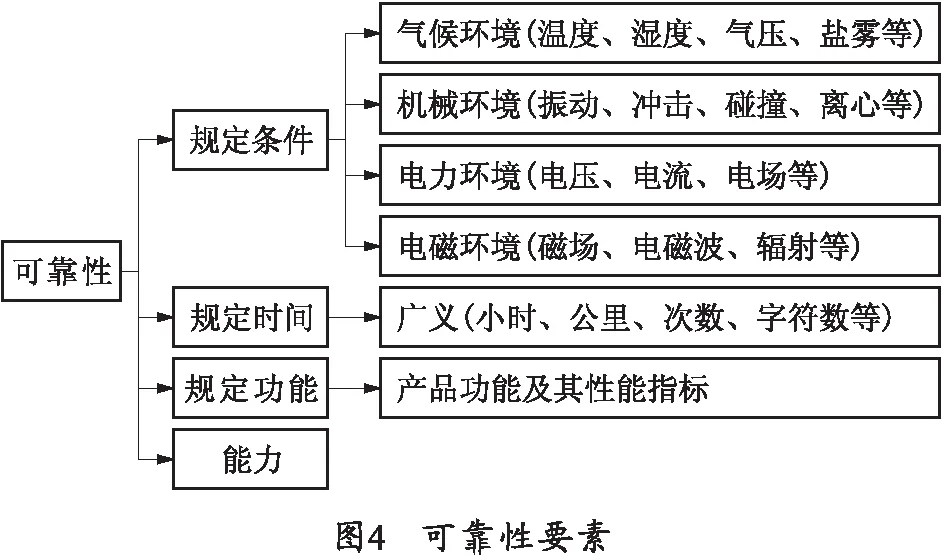
系统的可靠性是衡量产品质量的一项重要依据，按照国家标准，可靠性定义为产品在规定条件下和规定时间内完成规定功能的能力[5]，如图4所示。经常作为可靠性衡量的特征量有两类：一是以概率指标表示，如可靠度、失效率及失效概率等；二是以寿命指标表示，如平均寿命和可靠寿命等。

根据固态存储器电路的可靠性框图，拟选用GJB/Z 299C—2006《电子设备可靠性预计手册》中所给出的21类元器件概率指标作为衡量指标，采用元器件应力分析方法对固态存储器的可靠性进行预计分析[6]。除微电路外，大多数元器件工作失效率λp预计模型均为基本失效率λb与πE、πQ等一系列π系数相连乘的形式[7]。

对于电阻电容、接插件以及分立器件等常规电子元件，其典型失效率模型为

λPi=λbπEπQπX，

(1)

式中：λb为基本失效率；πE为环境系数；πQ为质量系数；πX为类别系数。

对于模拟电路及Flash存储等半导体单片集成部件典型失效率模型为

λPj=πQ[C1πTπV+(C2+C3)πE]πL，

(2)

式中：πT为温度系数；πV为电压应力系数；πL为成熟系数；C1、C2为复杂度失效率；C3为封装复杂度失效率。

因绝大多数电子产品和机电产品服从指数分布，则可靠度为

R(i)=e-λit，

(3)

式中：λi为元器件失效率；t为工作时间。

顶事件失效概率为

(4)

式中：Xi为最小割集；N为最小割集个数。

在许多实际工程问题中，多数零件可靠度较高，也就是底事件失效概率很小。因此在实际计算中，常取首项来近似：

(5)

2.2 故障树分析理论

故障树分析(FTA)[8]是在系统设计过程中对可能造成系统故障的各种因素进行分析，选取系统失效故障为顶事件，以运行状况和实践经验逐层搜索引起故障发生的中间事件和底事件[9]，通过逻辑关系图演绎，从而确定系统故障原因的各种可能组合方式或其发生概率，以计算系统故障概率。该方法通过定性分析和定量计算[10]，可以很好地分析出各底事件对顶事件的影响，具有准确、高效、形象等特点，在故障分析中得到了广泛应用[11-12]。

故障树分析的步骤如图5所示，其重难点是故障树建立以及定性定量分析。

2.2.1 定性分析

定性分析的目的是寻找导致顶事件发生的故障模式，明确导致系统顶事件发生的全部最小割集。每一个最小割集代表了系统的一种故障模式，只要在设计过程中能够保证每个最小割集中至少有一个底事件能够不发生，那么顶事件就一定不会发生。

2.2.2 定量分析

定量计算的目的是计算顶事件发生的概率，以及通过对底事件的重要度进行计算，分析底事件发生故障对顶事件发生的影响大小。

重要度分析[13]是故障树分析中的重要组成部分，不同的底事件在系统中呈现非均等的重要性。为了从不同角度评估各底事件对系统失效的贡献，有必要分析并计算底事件的重要度。重要度又分为结构重要度、概率重要度和关键重要度。

1)结构重要度反映单元在故障树结构中所处位置的重要程度，与该单元发生概率无关。其计算公式为

(6)

式中：Ist(i)为底事件关键重要度；ni为因第i个单元从正常变为故障而使系统由正常变为故障的次数。

2)概率重要度反映单元概率的变化对系统概率变化的影响程度。即各底事件对顶事件失效概率计算公式求一次偏导。其计算公式为

(7)

式中：Ipr(i)为底事件概率重要度；Pi代表底事件的失效概率；PT代表系统的失效概率。

3)关键重要度反映单元故障概率改进的难易程度。其计算公式为

(8)

式中：Icr(i)为底事件关键重要度；Ipr(i)为底事件概率重要度；Pi代表底事件的失效概率；PT代表系统的失效概率。

3 系统故障树模型计算

根据固态存储器的组成和测试原理，其可靠性模型应为串联模型，固态存储器随弹体飞行时间设计为1 000 s.

3.1 故障树建立

根据对存储记录电路的分析，建立该系统的故障树模型如图6所示，事件说明如表1所示。

表1 事件说明表

3.2 定性分析计算

定性分析的方法有上行法和下行法两种[14]，所谓下行法，就是由顶事件开始，由上而下逐级寻找事件集合，最终获得故障树的最小割集；所谓上行法，就是从底事件开始，由下而上逐级寻找事件集合，最终获得故障树的最小割集。笔者应用下行法对故障树进行定性分析。基本思想是：OR门使割集数目增加，AND门使割集容量增加。经分析，系统最小割集为{X1}，{X2}，{X3}，{X4}，{X5}，{X6}，{X7}，{X8}，{X9}，{X10}，{X11}，{X12}，{X13}.

3.3 定量分析计算

定量分析主要有两方面内容：一是通过底事件的概率来计算系统的概率；二是计算系统各底事件的重要度。定量分析涉及到众多参数的选取和繁杂的计算过程，其中质量等级划分为A、B、C三等，细分又可分A1～A6、B1～B2及C，笔者主要选取B等级进行计算。其他参数选取如表2所示。

表2 定量分析各事件参数选择

3.3.1 底事件概率计算

根据式(1)～(2)，将表2所列各参数带入对应的公式中，即可求各底事件失效率数值，如表3所示。

表3 基本事件及失效率

将固态存储器随弹体飞行时间和表3中计算出的底事件失效率代入式(3)，可知各底事件的可靠度R(i).查阅可知失效概率(即不可靠度)计算公式为

P(i)=1-R(i)，

(9)

则可知各底事件失效概率结果如表4所示。

表4 基本事件失效概率表

3.3.2 重要度计算

根据式(5)和(7)对各底事件的概率重要度进行计算得知，系统各底事件的概率重要度相等，且计算得出其值为Ipr(Xi)=1.

根据式(5)、(7)、(8)进行联合计算，将计算结果按照比例划分，系统各底事件的关键重要度结果及所占比例如图7所示。

3.4 FTA报告

通过定性分析，发现在失效故障中，13个底事件都可能导致顶事件的发生。因此，在研发过程中需加强对底事件的重视。同时，在进行定量分析及重要度排序过程中，由于各底事件结构重要度和概率重要度计算结果相等，因此着重参考关键重要度。通过对关键重要度进行百分比排序得知模拟电路(X5)、AD转换(X7)以及Flash存储(X9)在存储电路系统中占有较大比重。因此在存储电路设计中重点关注此三类元器件，尽可能选用更可靠稳定的厂商器件，同时加强筛选实验以避免偶然失效事件的发生。

3.5 实验验证

在某次实验测试中，测试过程如图8所示，模拟采编模块1通道10出现数据峰值过低问题，波形图如图9所示。

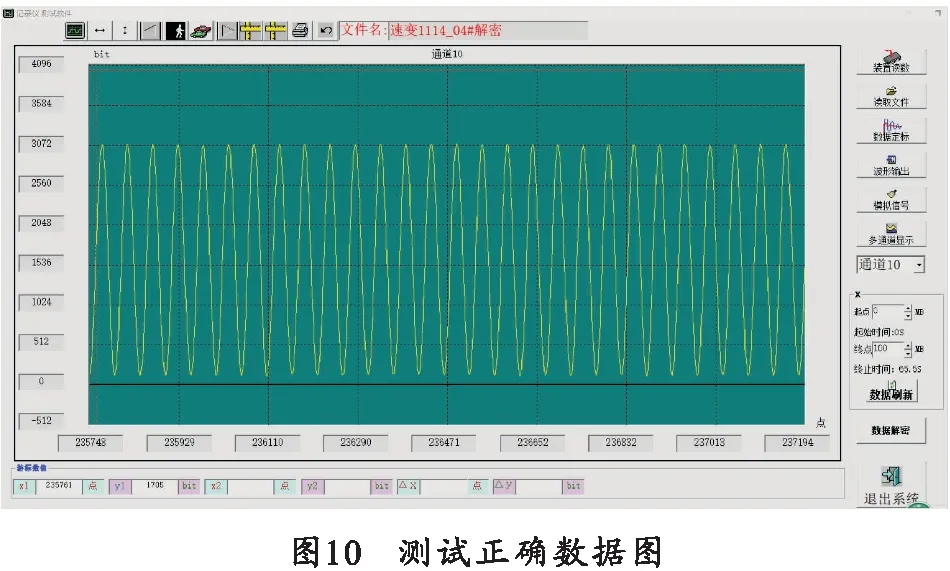
通过故障树定性分析找出底事件，参考前文定量分析中重要度比例大小进行排序检查，X9>X5>X7>X3>X6>X4>X8>X13>X10>X12>X11>X2>X1，在检查到第4步电阻部分时，发现此通道调理电路部分分压电阻有问题，在更换电阻后再进行数据的测试读取，读取结果如图10所示，结果显示正常。此次实验说明故障树分析可以很好地应用在固态存储器的故障定位上，方便人员快速进行故障定位。

4 结束语

针对固态存储器缺乏定性定量分析和故障难以定位的问题，提出了基于故障树分析的固态存储器可靠性研究。采用基于故障树的分析方法，研究固态存储器的系统组成和工作原理，按照元器件种类划分可靠性单元，建立故障树模型；对故障树进行定性分析找出底事件，确定引起系统失效的最小割集；进行定量分析计算各底事件失效概率及3种重要度,并对重要度进行排序，确定各底事件对系统的影响程度；最后以实验验证了故障树分析在固态存储器可靠性方面的可行性。

通过故障树方法中的分析计算，分析阐明系统的逻辑关系，从而对各部件的重要程度进行合理准确的判断，有助于人员快速定位故障位置，对合理高效地解决突发故障提供理论参考依据。通过这次分析发现，故障树分析可以很好地应用在固态存储器设计中，为提高固态存储器的可靠性提供科学指导。