侧孔参数对炮口制退器流场结构及超压的影响研究

徐 达，罗 业，张 杰，王春茂

(1.陆军装甲兵学院 兵器与控制系, 北京 100072；2.内蒙古北方重工业集团有限公司技术中心,内蒙古 包头 014033)

轮式轻型底盘加装大口径坦克炮是实现现役装甲装备更新换代的有力举措，在炮口添加炮口制退器是其中的关键技术之一。高膛压坦克炮相对于一般火炮具有装填密度大，膛压高，炮口剩余能量高的特点[1]，因此高膛压坦克炮安装炮口制退器后，一方面在膛口周围产生更强的冲击波超压，危害后方人员及设备；另一方面在炮口制退器内引起更强的扰动，影响射击精度；此外，对炮口制退器本身的强度也提出了更高的要求。这些问题的研究均以对膛口流场的气流发展规律及流场结构的深入认识为前提[2-5]。

大口径火炮射击时间极短且受膛口焰的干扰剧烈，难以通过试验获得流场数据及灵活研究参量变化对膛口流场的影响。随着CFD技术的发展，采用数值模拟方法研究大口径火炮膛口流场问题具有十分重要意义[6]。由于采用相同的侧孔结构时火药燃气通过各个侧孔的流量是递减的[7]，因此第1排侧孔的设计对身管后方冲击强度的影响最大，流入侧孔的流量及流速与侧孔轴线角度、侧孔孔径等参数有关[8]。

鉴于上述情况，为定性分析第1排侧孔参数对炮口流场的影响，笔者将炮口制退器模型简化为二维轴对称模型，采用有限体积法对适用于湍流和粘性流动的二维Navier-Stokes(N-S)方程进行离散化，结合具有二阶空间计算精度的AUSM+格式及结构化动网格技术，以初始冲击波到达膛口为起始时刻，对弹丸从膛内飞离膛口的过程中进行了瞬态数值模拟。以激波管实验及弹丸风洞实验为例，对采用的数值方法进行了实验验证。以125 mm坦克炮为例，研究了加装炮口制退器后膛口流场的发展过程，并对比了对第1排侧孔采用倾角为0°、10°及20°，孔径为20、30及40 mm时膛口周围压强的变化及产生机理。

1 数值模拟

1.1 控制方程

由于膛口流动为高超声速流，因此选取可压缩Navier-Stokes方程为流动控制方程，基于连续介质假设并忽略体积力及热源，笛卡尔坐标系下无量纲形式的二维轴对称非定常可压Navier-Stokes方程可表示为

(1)

式中：

式中，黏性系数μ的计算公式为

μ=μL+μT，

(2)

此外为使N-S方程封闭，还需添加气体状态方程，完全气体条件下，无量纲形式的气体状态方程为

(3)

式中：Ma为射流马赫数；T为温度。

采用有限体积法对方程(1)进行空间离散，离散项中无粘通量采用AUSM+格式离散，时间项的求解则采用二阶精度的Runge-Kutta法。笔者所研究的坦克炮采用的是坦克身管，因此只考虑弹丸沿轴线方向的平移，同时为避免非结构网格带来过多的数值耗散，采用结构网格，相应的动网格的更新方法采用动态分层模型。

1.2 计算模型

弹丸运动的计算域模型如图1所示，计算域被分割为膛内弹后的A区、膛内弹前的B区和膛外的C区，同时为实现仿真，通过添加滑移界面将整个计算域分为动网格区域和固定网格区域，其中动网格区域由膛内流域及沿轴线延伸至流域边缘的流域组成。

边界条件设置如下：膛底、身管及炮口制退器采用绝热固壁面；弹丸采用绝热运动壁面；C区的边缘采用压力远场；以身管轴线为轴对称边界(只取对称轴上半部分进行计算)；此外为减少计算域边界反射波对流场的影响，出口边界均采用非反射壁面条件。为充分研究身管后方超压变化规律并考虑到计算域的对称性，在以膛口截面中心为圆心，半径为1 m的1/4圆弧上取4个压强监测点，记为pi(i取1～4)；其中p1在膛口横截面上，p4在膛外壁上，p2和p3是膛口外壁面与p4之间线段等分点在圆弧上的投影。图1中各参数取值如表1所示，图中h和α分别表示侧孔孔径及相对膛口截面的倾角。

表1 125 mm坦克炮身管参数

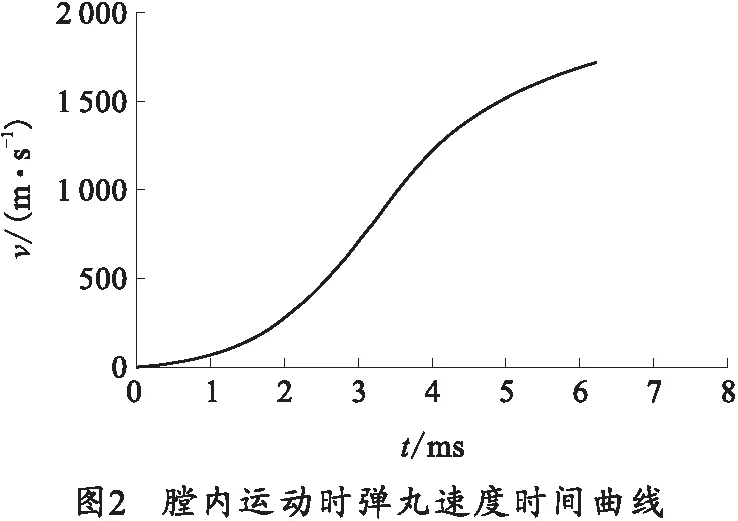
弹丸在火药燃气的作用下加速运动，假定弹丸周围气体随弹丸以相同速度运动，且运动规律已知，则初始冲击波到达膛口时，弹丸所在位置及位于弹头和初始冲击波之间的流场分布特性能够通过兰金-雨贡纽关系式及绝热冲击方程获得。据此，笔者以通过经典内弹道理论得到如图2所示的弹丸速度时间曲线为基础，得到了初始冲击波到达膛口时弹底至膛底距离l3=5 540 mm，并以此作为之后数值仿真的初始时刻(t=0).

弹后空间(A区)的初始条件如初始压力和速度沿内膛的分布等根据内弹道计算得到，其结果如图3所示；B区的流场分布取弹前和初始冲击波之间的流场计算结果，如图4所示。

C区气体为理想气体，气体分子量取23.5，温度和压力分别为T=293 K，Pa=101.3 kPa，粘性采用sutherland函数定义；弹丸的运动采用6DOF刚体运动模型来描述，其中弹丸质量为7.4 kg，惯性张量IXX=0.013 669 kg·m2,IYY=0.085 464 kg·m2.

为提高对激波的捕捉精度，对弹底和弹头周围的附体网格及膛口周围网格进行局部加密，整个计算域被划分为803 649个网格单元。

2 实验验证

膛口流场的发展主要受两种现象的支配，即冲击波在膛口处的衍射及超音速弹丸前方的弓形激波，由于实际中难以通过一个实验对二者进行综合验证，因此笔者分别采用激波管实验和弹丸飞行实验来对笔者所采用数值方法和计算模型的正确性及可信性进行验证。

首先，采用激波管实验对冲击波以Ma=1.6的速度从膛内运动至周围空气中，并在出口处绕边缘衍射的情况进行了数值模拟，计算域及边界条件的设置与图1类似，得到的数值纹影结果与文献[9]中实验纹影图的对比如图5所示。可见，除了很少的细微特征差别外，二者无论条纹的数量还是每条条纹的分布都能够很好地吻合，从而验证了笔者所用方法及模型的正确性。

其次，采用与本研究类似的计算模型(不考虑身管)对弹丸以Ma=3.6的速度在大气中水平飞行时的情况进行了数值模拟，仿真结果与文献[10]中实验结果的对比如图6所示。由图可知仿真结果与实验结果具有很好的一致性，实现了对动网格边界条件的验证。

3 计算结果及讨论

从初始时刻开始，炮口制退器流场发展主要包含以下4个过程：初始流场的发展、火药燃气流场的发展、弹体周围冲击波的发展及冲击波与弹丸的相互作用。

3.1 α=0°、h=40 mm时的膛口流场发展过程

图7为数值模拟结果的时间顺序图。图中对称轴上半部分为压力云图，对称轴下半部分为速度云图，并在速度云图中添加了能够反映涡旋特征的流线。

图7(a)表示初始冲击波从膛口冲出0.28 ms，即t=0.28 ms时的膛口流场特征。此时弹丸运动至膛口，弹前气流在弹丸的推动下依次从第1个侧孔、第2个侧孔及弹孔喷出，形成初始流场，流场结构具有以下特征：初始冲击波是弹孔和两排侧孔独立形成的初始冲击波合成的结果；侧孔分流射流及弹孔主射流在喷口处膨胀加速，剪切并卷吸周围空气，在前后侧孔及弹孔附近形成涡旋分别记为v1、v2、v3；侧孔与弹孔射流具有不同的流动特征，即在弹孔处二次冲击波沿轴线方向接近球形，而径向在涡旋v3的作用下，二次冲击波的边缘被卷吸入低压涡核中，形成稳定的“冠状”前沿，而在侧孔处由于两排侧孔射流间的相互干扰，二次冲击波的结构特征并不明显。此外，由第1排侧孔的速度云图可知，在侧孔入口处气流撞击中间挡板而改变方向，但主要沿中间挡板边缘膨胀喷出，从流线图可知，也有少部分气体向弹孔方向偏折并在两排侧孔射流间循环反射。

图7(b)表示t=0.34 ms时的膛口流场特征。从流线图可知，从第1排侧孔喷出的偏折向弹孔方向的气流也卷吸周围空气，而在第1排侧孔射流右侧产生涡旋v4；随着弹丸运动，从前方侧孔喷出的射流能量增加，冲击第1排侧孔射流后使其方向改变。此外从速度云图可知二次冲击波两侧的速度梯度很明显。

图7(c)表示t=0.46 ms时的膛口流场特征。此时弹丸封闭了侧孔，侧孔气流自由发展，从流线图可知，从前方侧孔喷出的射流冲击第1排侧孔射流后产生涡旋v5，并诱导产生旋转方向相反的涡旋v6.此时流场中逆时针旋转的涡旋有v2、v4、v5，顺时针旋转的涡旋有v1、v3、v6.

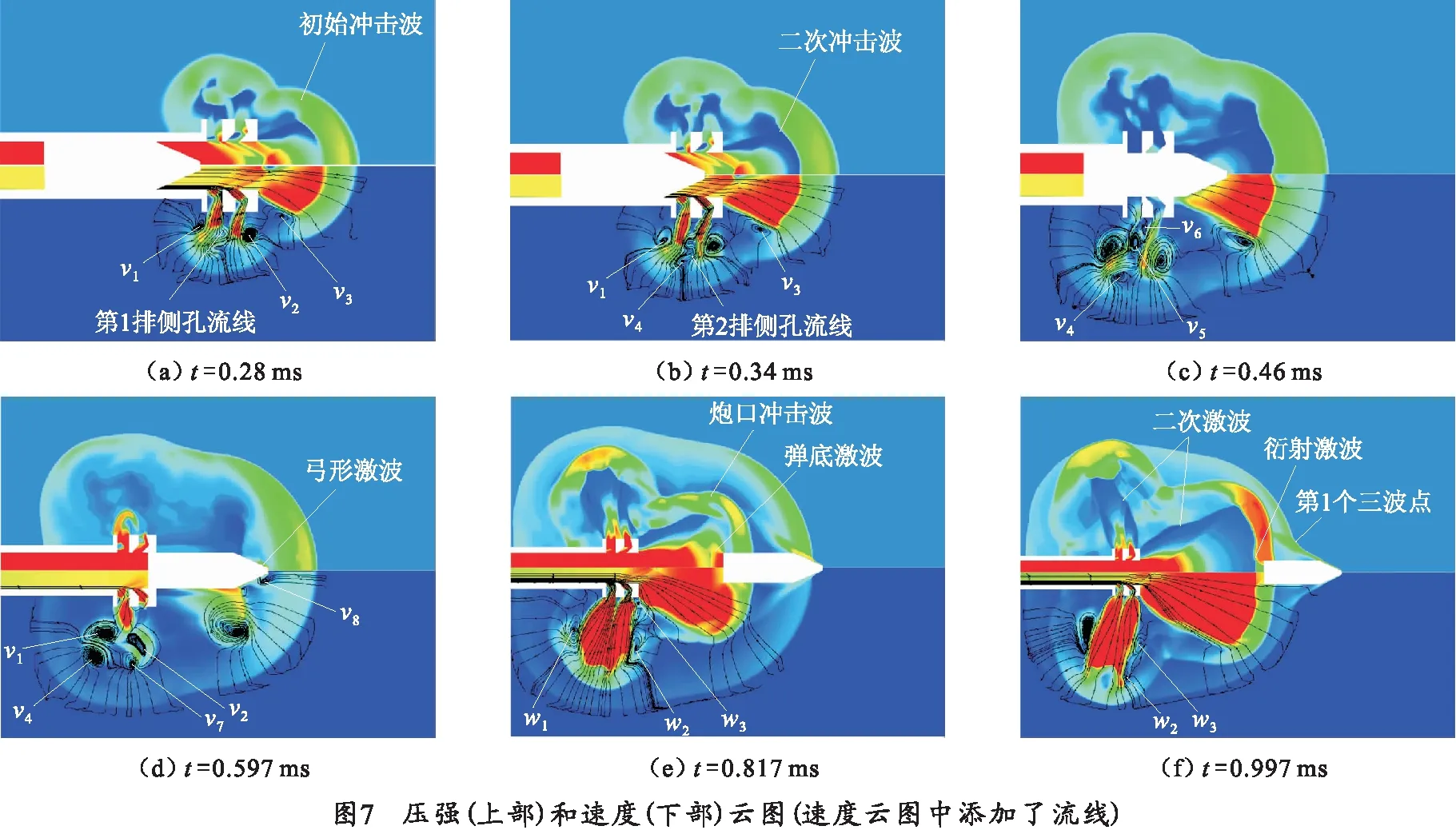
图7(d)表示t=0.597 ms时的膛口流场特征。此时弹头部从初始流场的二次冲击波中穿出；由于涡旋v2的环量大于涡旋v5的环量，因此v5移向v2并与之合并，使得v2的强度增加的同时诱导产生顺时针涡旋v7；此时由于弹丸相对周围气体超音速运动，因而在弹前产生弓形激波，与此同时在弓形激波后分离的流线与弹丸之间产生了涡旋v8，之后被涡旋v2合并；此时弹底到达弹孔，火药燃气从侧孔喷出，与初始射流类似，第1排侧孔中的膨胀射流被中间挡板反射后主要沿径向喷出。

图7(e)表示t=0.817 ms时的膛口流场特征。此时初始冲击波发展成为稳定的椭球面，且火药燃气流场的结构清晰可见，包括炮口冲击波及火药燃气流场的二次冲击波；由于燃气射流速度远高于弹丸速度，弹底压缩弹后气流，形成弹底激波；由于流体的粘性和斜压性，初始射流涡旋很快在具有很高能量的火药燃气作用下消失，并卷吸周围气体形成与初始射流中涡旋v1和v2类似的涡旋w1和w2；此外射流在右侧挡板下方产生与扰流问题类似的逆时针旋转涡旋w3.

图7(f)表示t=0.997 ms时的膛口流场特征。此时侧孔方向上的炮口冲击波率先赶上初始冲击波；弹丸移出激波栅格，二次冲击波在弹丸尾部发生衍射，产生衍射激波；弓形激波赶上初始冲击波后在相交点处产生了第1个三波点；与初始射流不同的是，火药燃气射流在侧孔和弹孔处均产生结构特征明显的二次冲击波；此外由于涡旋w2的环量大于涡旋w3的环量，因此w3快速移向w2并与之合并。

3.2 侧孔参数对流场结构及超压的影响

等口径炮口制退器的侧孔参数主要是指孔径及侧孔倾角，侧孔参数直接影响流入侧孔的流量，鉴于第1排侧孔的重要性，主要研究第1排侧孔参数改变时，膛口流场的动态特性。第1排侧孔参数取不同值时的膛口流场的动态发展过程基本一致，但膛口流场结构及超压分布随侧孔参数的改变呈现出一定的规律。

压强监测点p1取得超压峰值时的仿真结果如图8、9所示，图中均只取计算域的一半，为便于观察激波，图中采用压强等值线，且等值线数量在压强取值范围内取为50.

图8表示α=0°改变孔径h时的结果。由图8可知，随着孔径的增加，侧孔处的炮口冲击波球面逐渐向前方倾斜，同时侧孔处二次冲击波的变宽，弹孔处的二次冲击波变窄，这是由于孔径增加使得从第1排侧孔喷出的气体流量增加，而从弹孔喷出的气体流量减少，一方面使得第2排侧孔喷向身管后方的气流更多地被喷向径向的第1排侧孔射流所阻挡；另一方面侧孔射流获得的能量增加，而弹孔射流获得的能量减少。

图9表示h=40 mm改变倾角α时的结果。由图9可知，随着倾角的增加，侧孔处的二次冲击波逐渐向前方倾斜，甚至导致了图9(c)中弹孔处二次冲击波后方“变窄”，这是由于倾角增加使得侧孔气流被更多的喷向前方，弹前射流受到的扰动加剧引起的。

采用不同的侧孔孔径及侧孔倾角时的各监测点的超压峰值分别如图10、11所示。

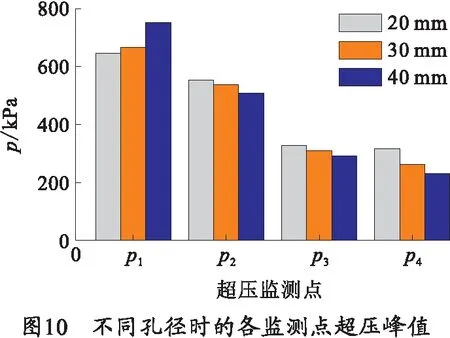
由图10可知，随着孔径的增加，p2至p4点的超压峰值降低，而p1点则相反，这是因为p2至p4点的超压主要受第2排侧孔射流的作用，孔径增加时第1排侧孔射流对前方侧孔射流的阻挡作用增强，使得喷向身管后方的气流减少，超压下降，而p1点位于第1排侧孔正上方，因此孔径增加的同时，射流对p1点的作用也增强，超压升高。由图11可知，随着倾角的增加，4个监测点的超压峰值均下降，由前面的分析可知，喷向第1排侧孔上方及后方的射流减少，导致压强下降。

4 结束语

考虑了炮口制退器第1排侧孔参数对膛口流场的影响，基于二维非定常Navier-Stokes方程，结合高精度AUSM+离散格式及结构化动网格技术，对弹丸诱导的炮口制退器流场进行了数值求解。仿真分析了具有两排侧孔的等口径炮口制退器流场的动态特性，揭示了冲击波/冲击波、冲击波/弹丸的相互作用机理及马赫盘、特征涡旋等流场特征的发展规律。对比侧孔参数对流场结构及超压的影响可知，侧孔处的炮口冲击波球面的方向主要受侧孔孔径的影响，而侧孔处二次冲击波方向主要受侧孔倾角的影响，此外随着侧孔倾角及孔径的增大，身管后方的超压峰值均下降，而膛口截面上p1点的超压峰值则呈现出相反的规律。笔者的研究为开展炮口制退器的结构设计及炮口扰动的研究提供了参考。