悬挂特性对某高炮射击密集度的影响研究
宁变芳,刘 欢,薛庆阳,赵 萌,单春来
(西北机电工程研究所,陕西 咸阳 712099)
悬挂是轮式武器系统底盘的重要组成部分,是连接武器系统车体和车轮的主要装置,其功能是衰减由车轮振动传递给车体的冲击。传统的圆柱弹簧悬挂结构形式简单、可靠性高,但是其空/满载车体高度变化幅度较大,无法实现悬挂参数与整车在不同承载状态下的良好匹配[1];而油气悬挂可以通过改变油气弹簧的充气压力来实现悬挂刚度变化,因此可适应武器系统不同负载及射击工况,具有良好的车炮匹配特性。
杨业海[1]对某高机动性越野车油气悬架系统进行了设计与开发,将所涉及的各种参数计算程序、仿真模型、优化算法及分析工具进行了整合与模块化,开发了油气悬架系统设计软件;徐文立[2]建立了油气悬架试验车的整车模型,研究了油气悬架对整车操纵稳定性和平顺性的影响;李魁武等[3]结合火控闭环控制技术,建立了误差综合补偿模型,利用火控解算前一时刻的误差特性,对后一时刻火控解算进行误差实时综合补偿,以提高射击精度。以上文献均未涉及悬挂特性对高炮射击精度的影响。
为了掌握悬挂特性对某轻型高机动平台射击精度的影响,采用集总参数识别方法获取了悬挂系统振动阻尼特性参数,研究了连发射击载荷下圆柱弹簧悬挂系统平台的振动特性。针对圆柱弹簧刚度不可调、车炮匹配性不佳的特点,研究了油气悬挂的刚度特性对车体振动的影响,优化后油气悬挂刚度可大幅度减小车体振动,从而实现车炮匹配优化。在模拟射击线稳定的补偿力矩作用下,该高炮可满足射击精度指标要求。
1 基于试验测试曲线的集总参数识别
1.1 集总参数单自由度自由振动特性分析
某轻型高机动武器系统采用6×6双横臂独立悬挂系统底盘,悬挂系统的阻尼特性参数一般通过试验获取,笔者通过对底盘振动特性分析和转膛自动机工作特性分析,将某轻型高机动高炮连发射击近似视为一个在高频(射击频率16.667 Hz,车体振动频率约1 Hz)激励作用下的单自由度强迫振动系统。
车体振动的单质量系统模型如图1所示。

该模型是由车身质量m和弹簧刚度K、减振器阻力系数为C的悬挂组成[4]。
车身垂直位移坐标z的原点取在静力平衡位置,根据牛顿第二定律,得到描述系统运动的微分方程为

(1)
令
(2)
那么,齐次方程为
(3)
式中:ωn为无阻尼时系统固有圆频率,而阻尼对运动的影响取决于n和ωn的比值ζ,ζ称为阻尼比:
(4)
汽车悬挂系统的阻尼比数值ζ通常在0.25左右,属于小阻尼,此时微分方程的解为
(5)


阻尼比ζ对衰减振动有两方面影响,与有阻尼固有频率ωd有关。
(6)
式中:ζ增大,则ωd下降;当ζ=1时ωd=0,此时运动失去振荡特征。汽车悬挂系统阻尼比ζ大约为0.25,ωd比ωn只降了3%左右,在工程上可以近似认为ωd≈ωn,车身部分无阻尼振动的固有圆频率ωn、无阻尼固有频率fn分别为
(7)
(8)
图2中两个相邻的振幅A1与A2之比d称为减幅系数,决定振幅的衰减程度,其表达式为
(9)
取自然对数:
(10)
可以由实测的衰减振动曲线得到减幅系数d,进而求出阻尼比ζ:
(11)
1.2 基于测试曲线的参数识别
基于摸底试验车体横滚角位移测试曲线,对该试验数据进行参数识别[5-6],测试曲线参数识别如图3所示。

得到:
(12)
(13)
(14)
(15)
(16)
通过分析单自由度高频强迫振动系统特性,认识系统的基本振动特性,为开展油气悬挂参数优化及车炮匹配分析奠定基础,也可更好地对射击线稳定采取有效补偿措施。
1.3 集总参数简谐激励下强迫振动与测试数据对比
针对原采用圆柱弹簧悬挂的底盘系统,基于识别的参数,建立了发射过程整车动力学模型,结合实弹射击试验,对侧向10连发射击载荷作用下的底盘振动响应进行验证,计算与测试曲线对比如图4、图5所示,测试曲线由安装于车体上的高精度陀螺姿态传感器[7]获取。


通过理论计算与测试值进行对比,计算车体横滚角位移最大值为71.2 mrad,测试横滚角位移最大值为70.4 mrad,计算误差1.2%,理论计算具有较高的精度,为开展悬挂参数优化奠定基础。
由图4、5可以看出,采用圆柱弹簧悬挂的底盘,由于圆柱弹簧悬挂的刚度具有不可调节的特点,使得车体在满载侧向射击工况下,其刚度表现较弱,10连发侧向射击工况下车体横滚角位移最大值达到约5°,车炮匹配性能不佳。
2 油气悬挂刚度特性分析
油气弹簧是用油液来传递压力[8],用压缩气体作为弹性介质的一种弹性元件。图6为油气弹簧的结构简图。

蓄能器(气室)内的气体状态方程:
P0Vr0=PVr,
(17)
式中:P0为开始充入蓄能器内的惰性气体压力;V0为开始充入蓄能器内的惰性气体体积;r为气体多变指数,一般r=1.28.
油气悬挂系统的刚度为[9]
(18)
式中:T0为油气弹簧的初始负载;x为正值表示油气弹簧活塞拉伸时产生的位移,负值表示油气弹簧活塞压缩时产生的位移;Af为气腔截面积。
从油气悬挂的工作原理以及力学特性可以看出,在油气弹簧内部油液往返流动的通道上设置阻尼阀和单向阀,可以使其自身就具有减振器的功能;油气悬挂具有非线性变刚性、渐增性的特性。
3 油气悬挂刚度对车体振动影响
油气悬挂通过改变油气弹簧的充气压力,即可实现油气悬挂的刚度变化,以实现适应不同负载工况,因此油气悬挂具有良好的车炮匹配特性[10-11]。
原武器系统底盘的悬挂系统采用圆柱弹簧,实弹横向射击时车体最大横滚角达到70.4 mrad,立靶密集度超差。
在原圆柱弹簧悬挂的底盘动力学模型的基础上,对油气悬挂刚度进行多方案对比分析,每次增大10%悬挂等效刚度,分析侧向射击工况条件下车体姿态横滚角位移、角速度变化情况,计算结果如表1所示。因版面所限,只列出部分车体姿态横滚角位移、角速度变化曲线,所示曲线对应表1中相应序号,如图7、8所示。

表1 油气悬挂刚度对侧向射击车体横滚角位移、角速度影响


由表1可知,应用油气悬挂刚度可调的优点,当车体前悬、中后悬挂等效线刚度各增大到256、316 N/mm时,车体横滚角位移降低到38.1 mrad,相对原圆柱弹簧悬挂试验炮降低了46.5%,车体横滚角速度降到158.3 mrad/s,相对降低了42.7%.
4 力矩补偿下射击密集度研究
基于对车体10连发侧向射击横滚振动基本特性和三相交流永磁同步电机(PMSM)负载扭矩响应特性,采用优化后油气悬挂刚度参数,构造与射速匹配的脉冲补偿力矩,实现对射击线稳定有效补偿。构造补偿力矩、炮膛合力、炮口角位移对应关系如图9所示。图中十字依次为第1~10发弹丸出炮口时刻炮口角位移量。

补偿力矩作用下炮口垂直及方位位移曲线如图10、11所示。
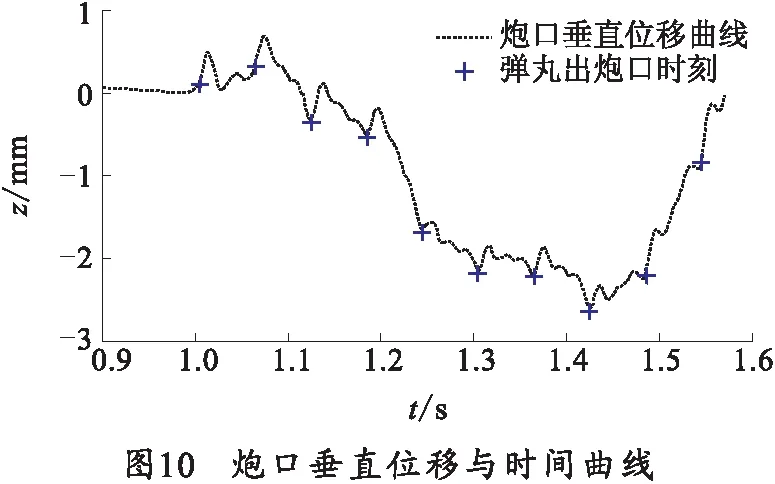

该高炮弹丸外弹道计算高低散布0.5 mrad,方位散布0.4 mrad;炮口振动引起的高低中间误差Ez及方位中间误差Ex分别为
(19)
(20)
由式(19)、(20)计算得到炮口振动引起的高低中间误差为Ez=4.574 mm,对应高低角位移中间误差为0.8 mrad;方位中间误差为Ex=2.4 mm,对应方位角位移中间误差为0.6 mrad.计算200 m立靶高低密集度为1.4 mrad,方位密集度为1.0 mrad.
根据分析计算结果,将该武器系统底盘悬挂系统由圆柱弹簧改为油气悬挂,经靶场5组实弹射击试验,横向射击200 m立靶密集度如表2所示,达到密集度指标要求。

表2 200 m试验立靶密集度
5 结论
1)根据油气悬挂刚度、阻尼可调的优点,在车体固有振动频率0.9~1.2 Hz易于实现的范围内,将车体前悬挂等效线刚度从128 N/mm增大到256 N/mm,中、后悬挂等效线刚度从158 N/mm增大到316 N/mm时,发现车体横滚角位移从71.2 mrad降低到38.1 mrad,降低了46.5%,车体横滚角速度从275.9 mrad/s降到158.3 mrad/s,降低了42.7%.
2)利用油气悬挂刚度、阻尼可调的优点,更易于实现车炮参数匹配,使系统振动位移、速度、加速度幅值降低,可有效减小随动补偿误差。
3)构造了与射速匹配的脉冲补偿力矩,计算表明,在补偿力矩作用下,该轻型高机动高炮侧向射击条件下高低立靶密集度为1.4 mrad,方位密集度为1.0 mrad,可满足高低及方位立靶密集度的指标要求。
4)对悬挂特性匹配优化后的武器系统进行了射击试验,横向射击5组,密集度试验均达到指标要求,验证了优化改进措施的有效性。

