复合优化问题的ε-对偶间隙性质和ε-强对偶*

田利萍，方东辉

(吉首大学数学与统计学院，湖南 吉首 416000)

1 问题的提出

inff(φ(x))

s.t.x∈C,h(x)∈-S.

(1)

特别地,当X=Z,φ为单位算子时,问题(1)即为如下经典的锥约束优化问题[10-14]：

inff(x)

s.t.x∈C,h(x)∈-S.

(2)

许多学者对复合优化问题进行了深入研究,得到了一系列有意义的结论.Bot等[1-2]在函数具有连续性、集合是闭集的情形下,刻画了无约束条件下复合优化问题与其对偶问题之间的强对偶和稳定强对偶.方东辉等[3-4]在函数不一定是下半连续函数、集合不一定是闭集的情形下,利用共轭函数的上图性质,等价刻画了问题(1)与其对偶问题之间的零对偶间隙性质、强对偶和Farkas引理.Boncea等[10]利用上图类条件和ε次微分类条件，等价刻画了问题(2)的ε-对偶间隙性质和稳定ε-对偶间隙性质.特别地,Boncea等[9]利用上图类条件和次微分类条件,建立了复合优化问题与其对偶问题之间的ε-对偶间隙性质、稳定ε-对偶间隙性质和ε-Farkas引理.受上述文献启发,笔者拟在函数不一定下半连续、集合不一定是闭集的情况下,通过引入新的约束规范条件,来等价刻画问题(1)与其对偶问题之间的ε-对偶间隙性质、ε-强对偶和ε-Farkas引理.

2 记号与定义

设X*,Y*和Z*分别是X,Y和Z的共轭空间,分别赋予弱*拓扑w*(X*,X),w*(Y*,Y)和w*(Z*,Z).〈x*,x〉表示泛函x*∈X*在x∈X处的值,即〈x*,x〉=x*(x).X的子集C的对偶锥和示性函数分别定义为

C⊕∶={x*∈X*:〈x*,c〉≥0,∀c∈C},

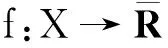
domf={x∈X:f(x)<+∞},

epif={(x,r)∈X×R:f(x)≤r},

f*(x*)∶=sup{〈x*,x〉-f(x):x∈X} ∀x*∈X*.

由文献[15]中的定理2.3.1可知,

f(x)+f*(x*)≥〈x,x*〉 ∀(x,x*)∈X×X*.

(3)

epif*+epig*⊆epi(f+g)*,

f≤g⟹f*≥g*⟺epif*⊆epig*.

(4)

定义f与g的下端卷积函数f□g:X→R∪{±∞} 为

(h+p+r)*(x*)=h*(x*-p)-r∀x*∈X*,

(5)

epi(h+p+r)*=epih*+(p,-r).

(6)

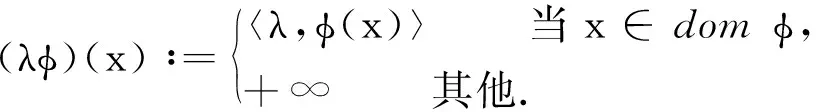
3 ε-对偶间隙性质和ε-强对偶

设p∈X*.考虑带线性扰动的复合优化问题

inff(φ(x))-〈p,x〉

s.t.x∈C,h(x)∈-S，

(7)

及其Lagrange对偶问题

(8)

特别地,当p=0时,问题(7)即为问题(1),而问题(8)转化为

(9)

令v(i)(i为问题对应的序号)表示问题的最优值,则有

v(7)≥v(8),

(10)

即问题(1)与(9)之间的稳定弱对偶成立.设A表示系统{x∈C;h(x)∈-S}的解集,即A∶={x∈C:h(x)∈-S}.如不加特殊说明,文中均假设A∩dom(f∘φ)≠Ø.

由共轭函数的定义，有

(11)

于是,对于∀r∈R和p∈X*,有

(p,r)∈epi(f∘φ+δA)*⟺v(7)≥-r.

(12)

如不加特殊说明,下文均假设ε≥0.

定义1(ⅰ)若v(1)-v(9)≤ε,则称问题(1)和(9)之间的ε-对偶间隙性质成立.

(ⅱ)若存在(λ,β)∈S⊕×domf*，使得对于∀x∈C，有

v(1)≤(βφ)(x)-f*(β)+(λh)(x)+ε,

则称问题(1)和(9)之间的ε-强对偶成立.

(ⅲ)若对于∀p∈X*,有v(7)-v(8)≤ε,则称问题(1)和(9)之间的稳定ε-对偶间隙性质成立.

(ⅳ)若对于∀p∈X*,存在(λ,β)∈S⊕×domf*，使得对于∀x∈C，有

v(7)≤(βφ)(x)-f*(β)+(λh)(x)-〈p,x〉+ε,

则称问题(1)和(9)之间的稳定ε-强对偶成立.

为了简便起见,记

为了研究问题(1)和(9)之间的ε-对偶间隙性质和ε-强对偶,引入如下约束规范条件:

epi(f∘φ+δA)*⊆Ω1-(0,ε),

(13)

epi(f∘φ+δA)*⊆Ω2-(0,ε).

(14)

(13)式称为(CQIε)条件, (14)式称为(CQε)条件.

命题1如下包含关系成立:

Ω2⊆Ω1⊆epi(f∘φ+δA)*.

(15)

证明设p∈X*.对于∀(λ,β)∈S⊕×domf*，有

于是,由(4)式可知Ω2⊆Ω1.接下来只需证明

Ω1⊆epi(f∘φ+δA)*.

(16)

(βηφ-f*(βη)+δC+ληh)*(p)≤r+η.

(17)

由(3)式可知，〈βη,φ(x)〉-f*(βη)≤f(φ(x)),∀x∈X,同时δC(x)+(ληh)(x)≤δA(x),∀x∈X,因此

(βηφ)(x)-f*(βη)+δC(x)+(ληh)(x)≤f(φ(x))+δA(x) ∀x∈X.

(18)

由(4)，(17)和(18)式可知，

(f∘φ+δA)*(p)≤(βηφ-f*(βη)+δC+ληh)*(p)≤r+η.

令η→0，则(f∘φ+δA)*(p)≤r,即(p,r)∈epi(f∘φ+δA)*，故(16)式成立.证毕.

注1(ⅰ)由命题1可知(CQε)条件⟹(CQIε)条件.

(ⅱ)当ε=0时,由(15)式可知(CQIε)条件转化为

epi(f∘φ+δA)*=Ω1,

(19)

(CQε)条件转化为文献[4]中的(CQ3)条件,即epi(f∘φ+δA)*=Ω2.

定理1(ⅰ)问题(1)和(9)之间的ε-对偶间隙性质成立，当且仅当

epi(f∘φ+δA)*∩({0}×R)⊆Ω1∩({0}×R)-(0,ε).

(ⅱ)问题(1)和(9)之间的稳定ε-对偶间隙性质成立，当且仅当(CQIε)条件成立.

证明因命题(ⅰ)和(ⅱ)的证明基本类似,故此处只证明命题(ⅱ).由共轭函数的定义可知，

(20)

于是,由(11)和(20)式可知,问题(1)和(9)之间的稳定ε-对偶间隙性质成立等价于

(21)

由(4)和(6)式可知,(21)式等价于epi(f∘φ+δA)*⊆Ω1-(0,ε),因此结论成立.证毕.

定理1等价刻画了问题(1)和(9)之间的ε-对偶间隙性质和稳定ε-对偶间隙性质.

当ε=0时,由定理1、注1(ⅱ)和(10)式可得如下结论：

推论1(ⅰ)问题(1)和(9)之间的零对偶间隙成立(即v(1)=v(9))，当且仅当

epi(f∘φ+δA)*∩({0}×R)=Ω1∩({0}×R).

(22)

(ⅱ)问题(1)和(9)之间的稳定零对偶间隙成立(即v(7)=v(8))，当且仅当(19)式成立.

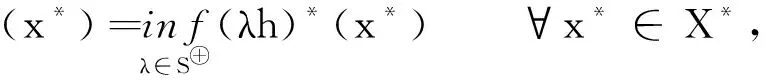
由(4)式可知，

注2文献[3]中的定理 4.2和定理 4.4分别利用约束规范条件

(23)

(24)

建立了问题(1)与其对偶问题

(25)

之间的零对偶间隙性质和稳定零对偶间隙性质.

命题2如下结论成立:(23)⟹(22),(24)⟹(19).

证明因“ (23)⟹(22) ”和“ (24)⟹(19) ”的证明基本类似,故此处只证明“ (24)⟹(19) ”.假设(24)式成立.由命题1可知,欲证(19)式成立,只需证明

(26)

又由(3)式可知,对于∀(λ,β)∈S⊕×domf*和y*,z*∈X*，有

〈z*,x〉-(λh)(x)+〈p-y*-z*,x〉-δC(x)+f*(β)=

〈p,x〉-(βφ-f*(β)+δC+λh)(x) ∀x∈X.

于是

从而(p,r)∈Ω1，故(26)式成立.证毕.

注3由共轭函数的定义可知,问题(25)与(9)等价.而由命题2可知,(23)和(24)式分别强于(22)和(19)式.因此,推论1改进了文献[3]中的定理4.2和定理4.4.

定理2下列命题等价:

(ⅰ)(CQε)条件成立.

(ⅱ)对于∀p∈X*,存在(λ,β)∈S⊕×domf*，使得

(f∘φ+δA)*(p)≥〈p,x〉-(βφ-f*(β)+λh)(x)-ε∀x∈C.

(27)

(ⅲ)设p∈X*，r∈R.若对于∀x∈A，有f(φ(x))-〈p,x〉≥-r,则存在λ∈S⊕，β∈domf*，使得

(βφ)(x)-f*(β)+(λh)(x)-〈p,x〉≥-r-ε∀x∈C.

(28)

(ⅳ)问题(1)和(9)之间的稳定ε-强对偶成立.

证明(ⅰ)⟹(ⅱ).假设(CQε)条件成立.令p∈X*，若(f∘φ+δA)*(p)=+∞,则(27)式成立.下设r∶=(f∘φ+δA)*(p)<+∞,则(p,r)∈epi(f∘φ+δA)*.由(CQε)条件可知 (p,r)∈Ω2-(0,ε),于是存在(λ,β)∈S⊕×domf*，使得

(p,r)∈epi(βφ-f*(β)+δC+λh)*-(0,ε),

即

(p,r+ε)∈epi(βφ-f*(β)+δC+λh)*，

从而

(βφ-f*(β)+δC+λh)*(p)≤r+ε.

(29)

由(3)和(29)式可得，

〈p,x〉-(βφ-f*(β)+λh)(x)≤r+ε∀x∈C,

因此(27)式成立.

(ⅱ)⟹(ⅲ).假设(ⅱ)成立.令p∈X*，r∈R.若对于∀x∈A，有f(φ(x))-〈p,x〉≥-r,则由(11)式可知,-(f∘φ+δA)*(p)≥-r. 又(ⅱ)成立,则存在(λ,β)∈S⊕×domf*，使得

-r≤-(f∘φ+δA)*(p)≤(βφ-f*(β)+λh)(x)-〈p,x〉+ε∀x∈C，

即(28)式成立.

(ⅲ)⟹(ⅳ).假设(ⅲ)成立.令p∈X*，-r∶=v(7)∈R,则对于∀x∈A，有f(φ(x))-〈p,x〉≥-r.由(ⅲ)可知,存在(λ,β)∈S⊕×domf*,使得对于∀x∈C,有

(βφ)(x)-f*(β)+(λh)(x)-〈p,x〉≥-r-ε,

于是

v(7)=-r≤(βφ)(x)-f*(β)+(λh)(x)-〈p,x〉+ε∀x∈C,

因此问题(1)和(9)之间的稳定ε-强对偶成立.

(ⅳ)⟹(ⅰ).假设(ⅳ)成立.任取(p,r)∈epi(f∘φ+δA)*.由(12)式可知,v(7)≥-r.又因(ⅳ)成立,故存在(λ,β)∈S⊕×domf*，使得

-r≤v(7)≤(βφ)(x)-f*(β)+δC(x)+(λh)(x)-〈p,x〉+ε∀x∈C,

于是

从而(p,r+ε)∈epi(βφ-f*(β)+δC+λh)*,即(p,r)∈Ω2-(0,ε),因此(CQε)条件成立.证毕.

定理2等价刻画了问题(1)和(9)之间的稳定ε-强对偶和稳定ε-Farkas引理.

当p=0时,由定理2可得如下结论：

定理3下列命题等价:

(ⅰ)

epi(f∘φ+δA)*∩({0}×R)⊆Ω2∩({0}×R)-(0,ε).

(30)

(ⅱ)设r∈R.若对于∀x∈A，有f(φ(x))≥-r,则存在(λ,β)∈S⊕×domf*，使得

(βφ)(x)-f*(β)+(λh)(x)≥-r-ε∀x∈C.

(ⅲ)问题(1)和(9)之间的ε-强对偶成立.

注4由注1(ⅱ)可知,当ε=0时,(CQε)条件和(30)式分别是文献[4]中的(CQ3)条件和定理3.6(ⅰ). 因此,结合(10)式可知,定理2和定理3分别推广了文献[4]中的定理4.1和定理4.4.

4 应用

设p∈X*,X=Z,φ为单位算子,则问题(7)转化为

inff(x)-〈p,x〉

s.t.x∈C,h(x)∈-S,

(31)

问题(8)转化为

(32)

当p=0时,问题(31)转化为问题(2)，问题(32)转化为

(33)

同时,(CQIε)和(CQε)条件分别转化为

(34)

(35)

于是，由定理1～3可得如下结论：

定理4(ⅰ)问题(2)和(33)之间的ε-对偶间隙性质成立，当且仅当

(ⅱ)问题(2)和(33)之间的稳定ε-对偶间隙性质成立，当且仅当(34)式成立.

定理5下列命题等价:

(ⅰ)(35)式成立.

(ⅱ)设p∈X*，r∈R.若对于∀x∈A，有f(x)-〈p,x〉≥-r,则存在λ∈S⊕，x*∈domf*，使得-f*(x*)-(δC+λh)*(p-x*)≥-r-ε.

(ⅲ)问题(2)和(33)之间的稳定ε-强对偶成立.

定理6下列命题等价:

(ⅱ)设r∈R.若对于∀x∈A，有f(x)≥-r,则存在(λ,x*)∈S⊕×domf*，使得

-f*(x*)-(δC+λh)*(-x*)≥-r-ε.

(ⅲ)问题(2)和(33)之间的ε-强对偶成立.

注5Boncea等[10]利用

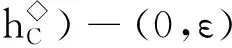
(36)

得到了定理4(ⅱ)的相关结论.由下端卷积函数的定义可知,(34)与(36)式等价，因此定理4(ⅱ)推广了文献[10]中的推论2.12.