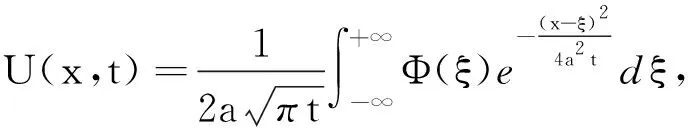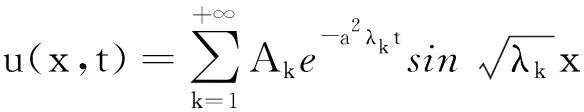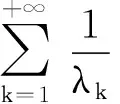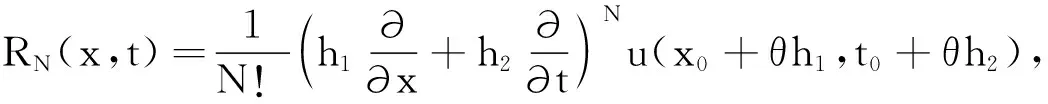热传导方程的解是解析函数的几种证明方法*
邢家省,杨义川,吴 桑
(1.北京航空航天大学数学科学学院,北京 100191;2.北京航空航天大学数学、信息与行为教育部重点实验室,北京 100191)
热传导方程的解是解析函数,这是热传导方程的一个深刻的结果,在偏微分方程的研究中起着重要作用.文献[1-16]对调和方程的解是解析函数给出了证明.奥列尼克[16]对热传导方程解的各阶偏导数给出了先验估计,证明了热传导方程的解是解析函数,但证明过程较复杂.笔者拟对热传导方程的解是解析函数这一结果给出几种简单直接的证明方法,以丰富热传导方程理论.
1 齐次热传导方程初值问题的解是解析函数的证明
对于齐次热传导方程初值问题
(1)
利用Fourier变换,可得形式解
(2)
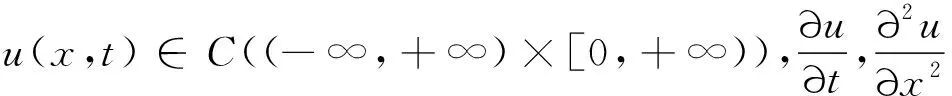
定理1设φ(x)在(-∞,+∞)上连续,且满足
|φ(x)|≤A+Ber|x|-∞ (3) 其中常数A,B,r>0,则(2)式所确定的函数u(x,t)∈C((-∞,+∞)×[0,+∞)),u(x,t)∈C∞(R×(0,+∞)),且u(x,t)是问题(1)的古典解. 证明令 由N>0,0<δ 定理2[1,15]设φ(x)∈C(-∞,+∞),且φ(x)有界,则对于每一个t>0,由(2)式所确定的函数u(x,t)是x的整解析函数. 定理3设φ(x)∈C(-∞,+∞),且φ(x)有界,则对于每一个t>0,由(2)式所确定的函数u(x,t)是x的整解析函数. 证明设|φ(x)|≤M,对于任意给定的t>0,存在δ>0,T>0,使得δ 记 定理3中初值函数的有界性条件可放宽为如下结果中的条件: 定理4设φ(x)∈C(-∞,+∞),且满足|φ(x)|≤A+Ber|x|(-∞ 定理4可仿照定理3进行证明. 考虑线性齐次热传导方程初边值问题 (4) 利用分离变量法和叠加原理,问题(4)的级数形式解为 (5) 在初值φ∈C[0,l],且φ(0)=φ(l)=0的条件下,由(5)式所确定的函数也是问题(4)的古典解[3,6].然而这个结果的证明要用到文献[12,15]中的方法. 设φ∈C[0,l],且φ(0)=φ(l)=0.对φ(x)进行奇、周期为2l的对称开拓,即定义Φ(x),使得 Φ(-x)=-Φ(x),Φ(x+2l)=Φ(x) -∞ Φ(x)=φ(x) 0≤x≤l. Ut-a2Uxx=0 -∞ 显然,U(x,t)关于x是奇函数,U(x,t)=-U(-x,t),U(0,t)=0(t>0).U(x,t)关于x是周期为2l的周期函数, U(l-x,t)=U(2l-l-x,t)=U(-l-x,t)=-U(l+x,t),U(l,t)=0t>0. U(x,t)是x的整解析函数. 其中α,β为非负整数.对于∀δ>0,当t≥δ时,有 (6) 对于任意给定的(x0,t0),t0>0,0≤x0≤l,存在δ>0,使得t0>δ.设x-x0=h1,t-t0=h2,则函数u(x,t)在(x0,t0)处的泰勒展开式为 即u(x,t)可展开成收敛的幂级数,故u(x,t)是(x,t)∈[0,l]×(0,+∞)的解析函数. 由解的唯一性可知,线性齐次热传导方程初边值问题的解是解析函数.
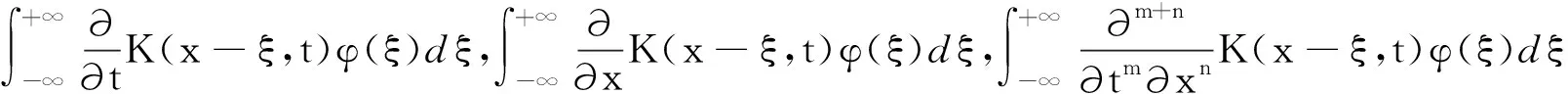
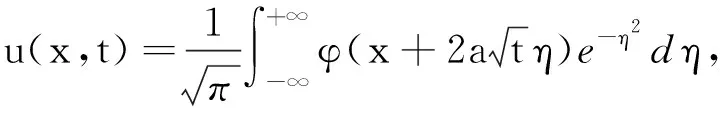


2 线性齐次热传导方程初边值问题的级数形式解的收敛性


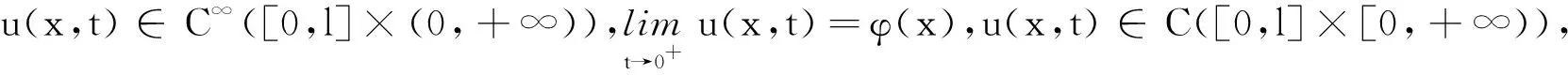
3 线性齐次热传导方程初边值问题的解是解析函数的证明