基于子阵的稀布阵列天线优化方法
丛友记,周 雷,吴苏兴,彭 芃,黄彩华
(中国船舶集团有限公司第八研究院,南京 211153)
0 引 言
相控阵体制雷达具有抗干扰能力强、搜索和跟踪目标快、可靠性高等优势,是现代雷达的发展方向之一。在相控阵雷达系统中,为了满足战技指标要求,一般含有几百乃至上万个有源通道,制造成本很高,系统非常复杂。稀布阵列可以在降低系统成本和复杂性的同时又不显著降低天线性能[1],在满足某些技术指标的前提下可以大规模减少有源通道数,是降低阵列天线成本与复杂度的技术途径之一,同时还有利于阵面散热提高可靠性。然而,稀布阵列一般存在扫描范围较小、较易出现大副瓣等缺陷。因此,在稀布阵列优化设计中需要解决这些问题。[2]
当前,对于稀布阵列天线优化主要有经典的统计法[1]、群智能优化方法[2-3]、迭代傅里叶变换法[4]、压缩感知与稀疏重建法[5]等等。这些方法均具有一定的局限性,如经典的统计法需要进行多次试探优化才能达到优化目标,群智能优化方法收敛时间长且较易陷入局部最优解,迭代傅里叶变换法需要天线阵元均匀栅格排列,而压缩感知与稀疏重建方法往往求解结果的健壮性不好。这些方法在工程应用中受到了限制。本文将以一非均匀分布的满阵作为模板,将经典的统计法与群智能优化方法结合,并利用NUFFT技术加速计算,解决了基于子阵的稀布阵列天线的优化设计问题。
1 优化设计方法
1.1 稀布阵列优化方法
稀布阵列设计问题就是在给定阵列形状的情况下如何确定阵元位置以最大限度地降低阵列旁瓣。由于阵元位置与最大旁瓣电平之间是复杂的非线性关系,目前还没有相应的解析解,因此只能采用非解析的方法得到相应的阵元位置解。传统的经典稀布算法有试探法、确定法、统计法等,其中针对等间距栅格状稀布阵列主要有统计法。本文将经典的统计法与差分进化(DE)结合在一起的优化方法来对稀布阵列进行优化,以下简要介绍这种方法。
所谓统计法就是不等间距阵在等间距阵地栅格上以参考分布作为概率密度函数随机地放置或者不放置单元而构成的。如果Aij表示第i行j列单元的振幅值,且有0≤Aij≤1,则此等间距阵的阵因子或方向图函数可写为
(1)
不等间距阵的间距常常是某一间距的整数倍,因此可把这种不等间距阵划分成许多等间距的栅格。在阵的栅格上随机地确定是否放置单元,即每个栅格上的单元幅度fij可为1或者0,这全部由概率决定。如令:fij=1放置单元的概率为Aij,fij=0无单元的概率为(1-Aij)。fij为一随机变量,则该阵列的方向图函数为
(2)
此阵因子的均值为
(3)
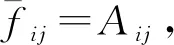
fij=1,Rij≤Aij
(4)
fij=0,Rij>Aij
(5)
当fij=1时放置单元,fij=0时则不放置单元。按上述步骤对全部单元进行判断,决定取舍。这样就可以确定单元排列位置并计算阵列的方向图,并判断是否满足预先给定的方向图指标,如不满足则重复以上过程直至获得满意的结果为止。统计法往往需要多次试探优化才能达到给定的优化目标。
为了得到更好的结果,本文首先利用经典的统计法在种群中寻得的多个解集作为初始种群,然后利用差分进化进行优化得到当前的最优解。算法流程如图1所示。
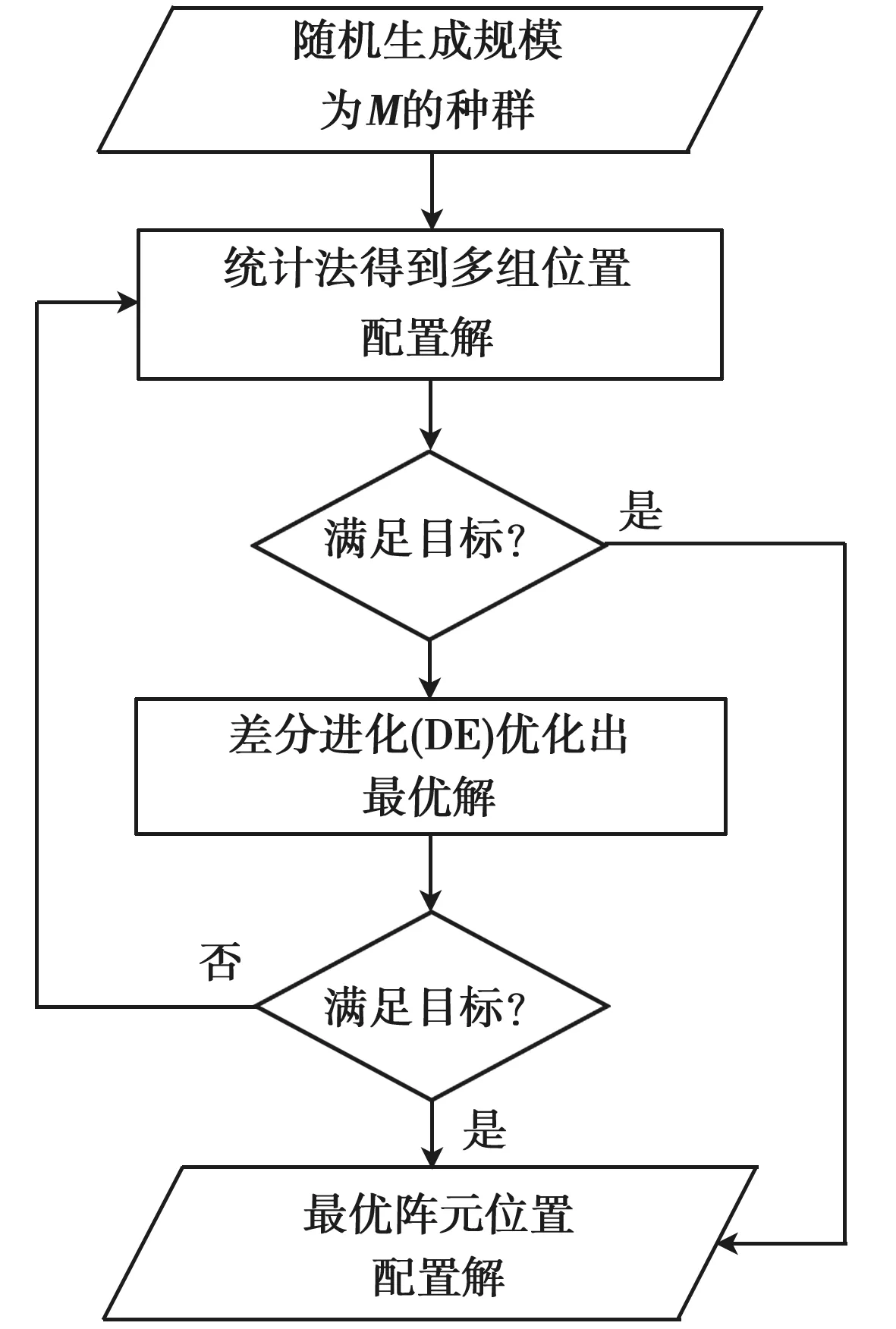
图1 算法流程图
本文的优化目标是阵列副瓣指标。为了抑制扫描状态时阵列天线的副瓣,本文将单元的排列非周期化。上述算法中的统计法是基于某一非均匀栅格的满阵模板进行的。由于本文是在非周期阵列上进行稀疏优化,优化过程中需要对非均匀阵列天线方向图进行反复计算,本文采用了NUFFT方法对方向图计算加速。
1.2 非均匀阵列方向图高效计算方法
对于非周期结构的天线单元,由于无法采用快速傅里叶变换法进行快速计算方向图,而利用传统的计算方法计算其三维方向图将十分耗时,因此本文采用了NUFFT技术进行优化加速。该算法的思想是将非周期阵列中的每个阵元都通过一个虚拟均匀阵列中的几个阵元来近似表示,通过优化这个虚拟均匀阵列的权值使得达到目标阵列方向图,最后真实的阵元激励通过虚拟阵列激励得到。
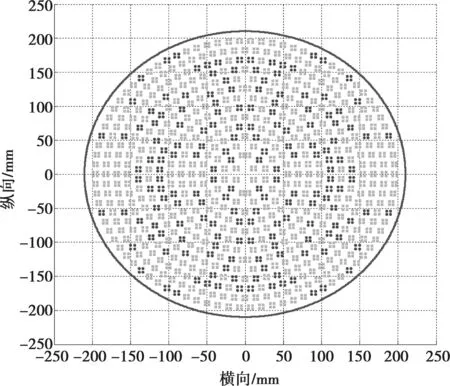
对于在x轴上的N元非周期阵列,假设其阵元位置为[x1,x2,x3,…,xN]T,其中xn为第n个阵元位置,并满足x1 (6) 其中,w=[w1,w2,w3,...,wN]T为阵列激励;u=cos(φ),φ为方位角度(从x轴测量);λ为波长。为解决非均匀阵元快速计算问题,可以将非周期阵列插值为一个虚拟的均匀阵列[6]。对于阵列中的每个阵元,将其阵元因子用几个虚拟均匀阵元的阵元因子加权叠加来近似(即用虚拟均匀阵列中的一个子阵的阵因子来近似),对于第n个阵元的阵元因子ej2πxnu/λ,可以用下式近似表示: (7) 其中,q为一个偶数;cn=2xn/λ;t=uM/2;L=rM,M=⎣cN-c1」+p,[x]与⎣x」分别表示与x最近的整数和大于x的最小整数,p为一个正整数,L为整数,r为过采样系数且大于1;a(xn)=[a-q/2(xn),…,aq/2(xn)]T为位置的复系数,q+1为对每个阵元因子插值时选择的虚拟阵元个数。非周期阵列被插值为一个虚拟的L阵元阵列。非周期阵列中的每个阵元用虚拟阵列中与该阵元位置邻近的几个阵元来插值得到。如图2所示,在实线框中的9个阵元(q=8)用来插值真实阵列中的第1个阵元。 图2 阵列插值示意图 为了计算ak(xn),首先均匀地在[-1,1]区间对u采样M点,然后将式(7)写为矩阵形式: Gna(xn)=vn (8) 其中 a(xn)=[a-q/2(xn),…,aq/2(xn)]T (9) (10) vn=[ω(-M/2)rcn,ω(-M/2+1)rcn,…,ω(M/2-1)rcn]T (11) 式中,ω=ej2π/L。由于M>>q,因此式(8)为超定方程,利用最小二乘法求得 (12) 得到系数a(xn)后,将式(2)代入式(1)中可得 (13) 其中,t∈[-M/2,M/2]为虚拟空间域,β=Tw,β=[β1,β2,…,βL]T。变换矩阵T的第1行第n列元素为 (14) 向量β为虚拟均匀阵列激励。由于虚拟阵列为均匀阵,可以应用FFT方法对方向图的计算进行加速,采用该方法后稀布阵的优化效率得到了极大的提升。 本文以某圆口径阵列天线为例对阵列天线进行稀布设计。该阵列天线为宽角扫描的圆极化天线,由于单圆极化天线单元在阵中很难实现宽带宽角扫描的要求。本例中采用了4个单极化天线依次相位滞后激励的原理实现了圆极化特性,并可以通过改变相位滞后顺序实现左右旋圆极化的切换。圆极化天线单元拟将4个单元作为最小的天线子阵单元进行稀布优化布局。由于阵列天线有方位、俯仰和差波束的需要,阵面4个象限需要镜像对称设计,因此在本例中上节所述的优化设计方法需要在4象限对称的约束条件下进行。 根据阵列天线波束宽度,整个天线口径为420 mm,若满阵布置的话需要2 544个射频通道。采用本节所述方法后,稀布后的子阵式阵列天线其有效射频通道数仅为满阵的27.4%(696个射频通道),大规模降低了射频通道数。基于圆环阵的子阵级稀布优化后的单元分布如图3所示。为了保证天线单元的阵中电磁环境的相对一致性,本文拟在接有射频通道天线单元周围布置“哑元”。 图4给出了稀布后的阵面典型波位的三维波束情况。从图中可以看出,扫描范围内阵列天线副瓣基本在-15dB以下,阵列波束扫描至60°时未出现栅瓣。 为了比较稀疏后的阵列性能与满阵阵列性能,本文将稀布前后的波束宽度、副瓣、增益等指标进行了计算,各项指标对比如表1所示。 从表中可以看出,稀布阵的波宽、副瓣等指标与满阵基本相当,但方向性系数下降较多。这也是稀布阵列带来的代价。从案例可以看出,本文所述的基于子阵的稀布阵列天线优化方法是有效的。 图3 阵列单元排布图(黑点表示激励单元, 灰点表示哑元) 稀布阵列与口径相同的满阵阵列天线具有几乎相同的主瓣宽度,其以较少的阵元数目实现了相同的分辨率。稀布阵不仅减少了阵列天线的制造成本,还大大降低了系统复杂性,提升了可靠性。本文通过在经典统计法的基础上结合群智能优化方法的混合优化算法对稀布阵列天线副瓣进行了优化设计,同时还利用阵列单元的非周期性排列抑制了天线扫描出现的远区副瓣。对于非周期性排列的阵列天线方向图的计算可以采用NUFFT技术进行加速。为了验证本文所述方法的有效性,本文以某圆口径圆极化阵列天线为研究对象,对该阵列进行了稀布优化设计。稀布后的通道数较满阵降低了72%以上,且波束宽度、副瓣等性能指标与满阵基本相当。本文所述方法可以为工程中相关稀布阵列天线优化问题提供参考。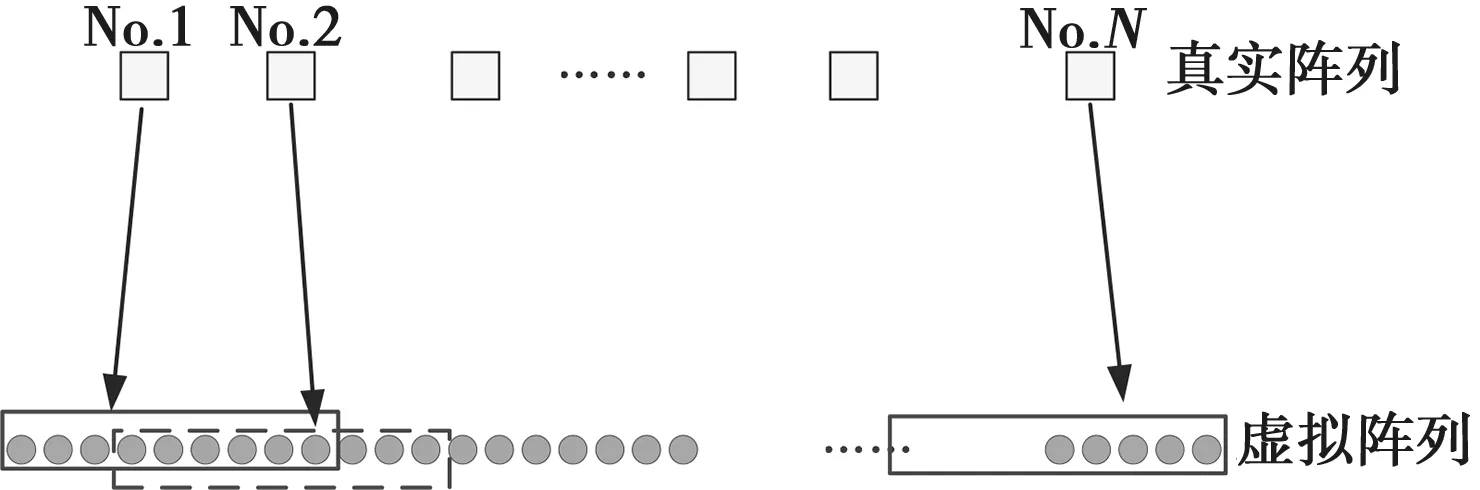
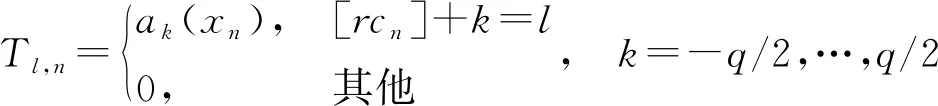
2 仿真案例
3 结束语

