分布式RS码的协作及基于权重分配的联合译码研究
张立康,仰枫帆
(南京航空航天大学 电子信息工程学院,江苏 南京,211106)
0 引言
在过去的几年中,许多作者研究了不同的信道编码在协作通信系统下的性能表现,包括低密度奇偶校验码 (Low Density Parity Check,LDPC)[1],Turbo码[2]和Polar码[3]等,但关于协作通信下的RS码的研究却很少。里德-所罗门 (Reed Solomon Code,RS)码是当今无线通信系统中使用最广泛的编码方案之一,已经被几种3G标准采用,包括数字视频广播(Digital Video Broadcasting,DVB) 标准[4]以及全球微波接入互操作性 (Worldwide Interoperability for Microwave Access,WiMAX)标准等[5]。
协作分集是最近引入的分集技术,利用中继节点来改善系统的范围和可靠性。最常见的协议是解码转发 (Decode and Forward,DF)协议和放大转发(Amplify and Forward,AF)协议 。在DF协议中,中继首先从源广播中解码信号,重新编码并将其转发到目标[6]。AF协议中,中继放大接收到的信号,并将放大后的信号转发到目的地[7]。将不同的信道编码方案与所述的中继协议集成,可以进一步提高协同系统的性能。这些类型的方案,也称为分布式编码,显著提高了协作系统的端到端性能[8]。RS码,作为一种极大距离可分码 (Maximum Distance Separable,MDS),广泛用于分布式存储[9],以求更好地达到冗余和可靠性的权衡点,已经被证实为最好的检错编码[10]。在无线通信的过程中,无限信道的衰落特性与通信质量息息相关,协作技术的提出有效地改善了信道衰落对无线通信质量的影响[11],但是基于RS码的协作研究是非常少的。
本文提出了一种新的基于分布式RS码的权重协作方案,由于不同信道条件对判决结果所带来的影响不同,利用源节点和中继节点到目的节点的信道条件的差异性和多进制正交振幅调制(Multiple Quadrature Amplitude Modulation,MQAM)硬判决的特性[12],在目的节点对两路信号权重分配后,采用文献[13]中提出的伯利坎普(Berlekamp) 迭代译码算法进行联合译码。通过实验仿真证明了该方案具有良好的性能增益,同时也从数学理论角度对该算法进行了推导,为该方案提供了理论依据。
1 RS码的编码与译码
1.1 RS码编码
符号取自GF(q)、纠t个错误的RS码,其生成多项式h(x)以α,α2,…,α2t为其全部的根,这是文献[14]中给出的定义,如式(1)所示:
h(x)=(x-α)(x-α2)…(x-α2t),
(1)
式中,αi为GF(q)中的元素,0≤i≤2t。RS码具有如下参数:
分组长度:n=q-1,
(2)
奇偶校验符号数:n-k=2t,
(3)
维数:k=q-1-2t,
(4)
最小距离:dmin=2t+1。
(5)
从另一个角度来说。RS码是商环R=Fq[x]/(xn-1) 上的主理想[15],其中R是主理想环(每个理想环都可以由单个元素生成)。
令u(x)=u0+u1x+…+uk-1xk-1为消息多项式,其中uj∈GF(q),0≤j≤k-1,编码过程是一种映射[16]:
ρ:u(x)→v(x)。
(6)
其中,系统级RS码的编码过程是:
v(x)=u(x)xn-k-[u(x)xn-kmodh(x)]。
(7)
1.2 Berlekamp译码算法
w(x)=w0+w1x+…+wn-1xn-1,
(8)
r(x)=r0+r1x+…+rn-1xn-1,
(9)
e(x)=r(x)-w(x)=e0+e1x+…+en-1xn-1,
(10)
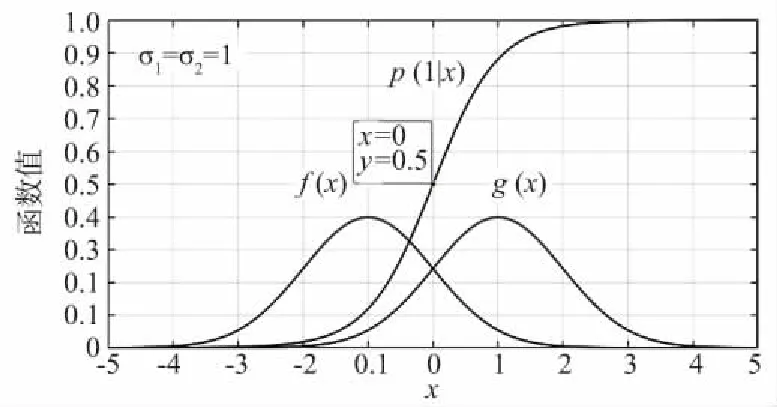
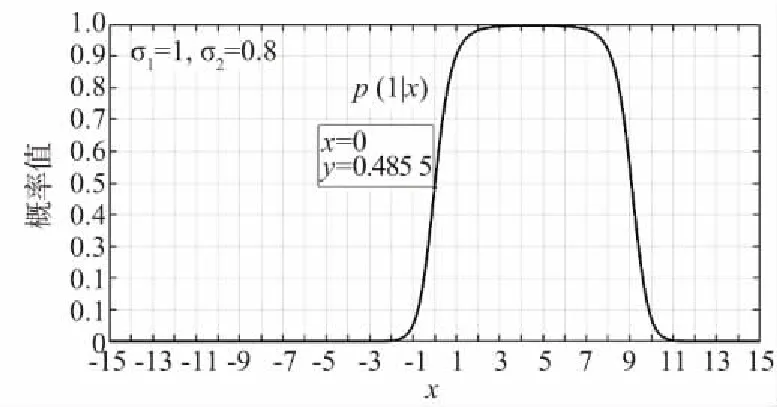
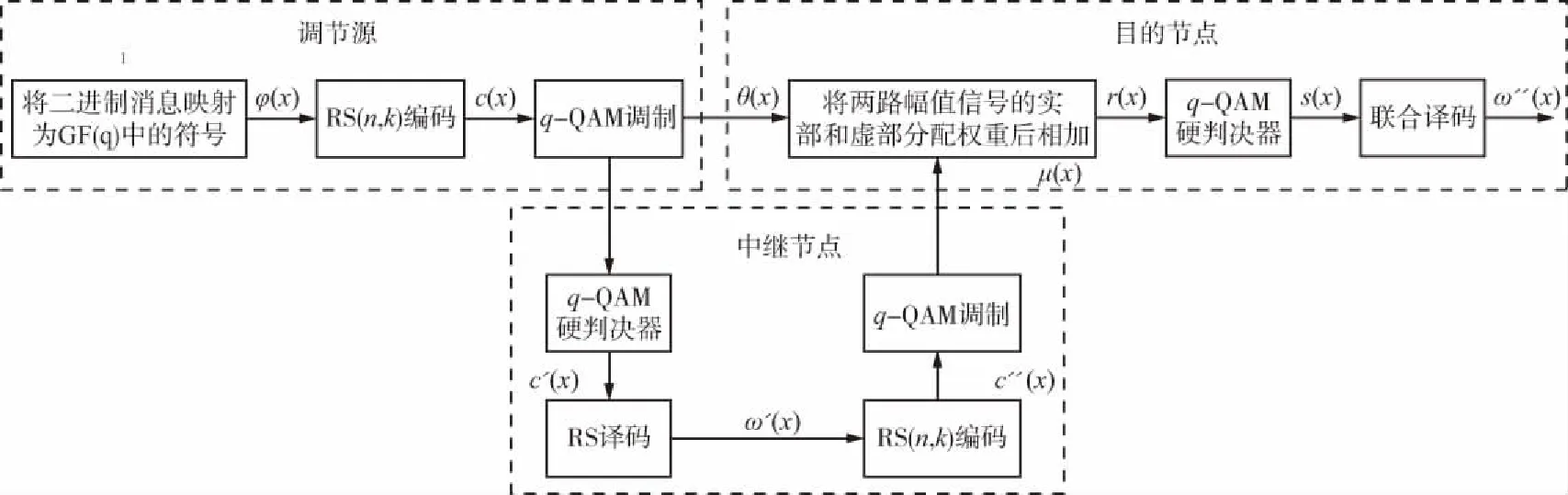
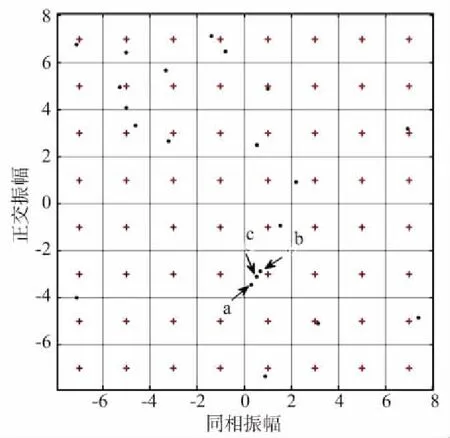
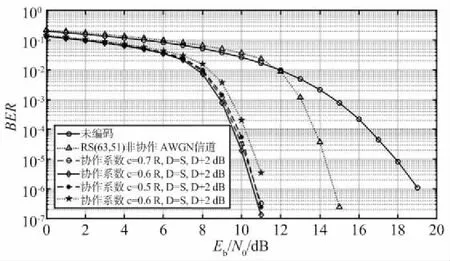
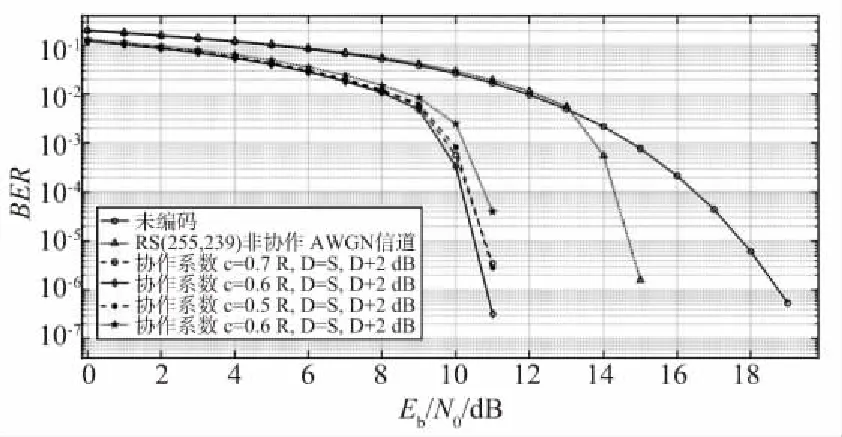
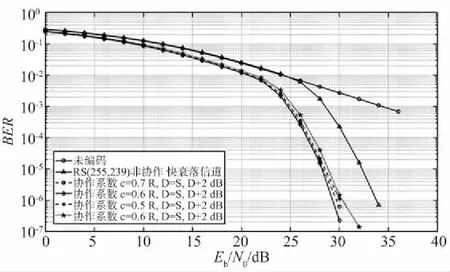
式中,w(x) 为传输的码多项式;r(x) 为接受多项式;e(x) 为错误模式[17]。由定义得ei=ri-vi,ei是GF(q)中的符号,假设e(x)在位置xb1,xb2,…,xbv上v个错误,其中0≤b1 e(x)=eb1xb1+eb2xb2+…+ebvxbv。 (11) 同时定义矫正子如下: Mi=e(αi),1≤i≤2t,α1,α2,…,α2t∈GF(q)。 (12) 对于1≤i≤v,令βi≜αbi,μi≜ebi。 定义错误位置多项式为: δ(x)=(1-β1x)(1-β2x)…(1-βvx)= δ0+δ1x+…+δvxv=1+δ1x+…+δvxv。 (13) 译码步骤为: (1) 计算矫正子(M1,M2,…,M2t)。 (2) 确定错误位置多项式: 在求解错误位置多项式的过程中,设定: δ(-1)(x)=1, (14) δ(0)(x)=1, (15) δ(1)(x)=1-M1x。 (16) 需要经过2t次迭代后取得错误位置多项式δ(x)=1+δ1x+…+δvxv,其中迭代方程如下: 1≤s≤2t-1,-1≤ρ (17) ρ的取值于[-1,s]范围内使得{ρ-lρ}的值最大的值,其中,ls和lρ为δ(s)(x)和δ(ρ)(x)的多项式的阶,ds和dρ的定义如下: (18) (19) 经过2t次迭代后,得到δ(x)=1+δ1x+…+δvxv,自此确定了错误位置多项式。 (3) 确定错误估值函数: 求得δ(x)的根,并求得这些根的倒数集{β1,β2,…,βv},并定义错误估值函数: (20) (21) (22) 整理得: (23) 相对于传统的点对点或者一点对多点的蜂窝网络,协作网络基于复杂的相互作用,所涉及的节点彼此协作,从而改善自己的通信性能[19]。基于中继节点的协作通信已经成为提高网络覆盖、频谱与功率效率以及减少中断概率的有效方法[20]。 2.1.1 AWGN信道 加性高斯白噪声(Additive White Gaussian Noise,AWGN) 信道是常见的通信研究信道,噪声是符合N~(0,σ2)的高斯白噪声,其条件概率密度函数如式(24)所示: (24) 对于RS(63,51) 码,采用的是64-QAM的调制方式,MQAM是一种将多进制数字相位键控(Multiple Phase Shift Keying,MPSK) 和多进制幅移键控(Multiple Amplitude Shift Keying,MASK) 结合起来的调制技术。可知SNR=Eb/N0+10lg(K/N)+10lg(lb(M)),其中K为信息位长度,N为码长,M为调制的阶数。在信号功率一致时,噪声功率不同的加性高斯白噪声概率密度函数的方差不同。 为了方便解释权重加法的原理,这里基于AWGN信道下的1 bit情况的2PSK调制进行讨论信噪比不同所带来的影响。 (25) (26) 根据PDF的定义,当收到1 bit信息x时,判决为-1的概率p(-1|x)为: (27) 判决为1的概率p(1|x)为: (28) 当σ1=σ2=1时,f(x),g(x)及p(1|x)的函数图如图1所示。 图1 f(x),g(x) 和 p(1|x) 的数学函数图Fig.1 Mathematical function diagram for f(x),g(x) and p(1|x) 图1的横坐标为自变量x的取值范围,纵坐标为对应函数的值。当σ1=σ2=1时,1 bit信息x加噪前为1的概率满足图1中的函数p(1|x),在x=0时,加噪前为1和-1的概率都为0.5。在x>0后,加噪前为1的概率大于0.5,并逐渐趋近于1。当σ1=1,σ2=0.8时,p(1|x)的函数图如图2所示,图2的横坐标为变量x的取值范围,纵坐标为条件概率函数p(1|x) 的取值。 图2 条件概率函数 p(1|x) 的数学函数图Fig.2 Mathematical function graph of conditional probability function p(1|x) 由图2可知,在x=0时,函数的值为0.485 5,此时加噪前为1的概率小于加噪前为-1的概率,这是由于方差不同所带来的对置信率(即判决结果的可靠性)的影响。 对于协作方案,做一个假设,设从源节点发送来的1 bit信息为x1=a+n1,从中继节点发送来的1 bit信息为x2=a+n2。假设中继节点到目的节点的信道的SNR要比源节点到目的节点的信道的SNR大2 dB,即: SNR(r,d)=SNR(s,d)+2。 (29) 即噪声n1的概率分布函数的方差比噪声n2的概率分布函数的方差要大,因此在这种条件下,从概率分布的角度上说,x1的置信率要比x2稍大。令权重加法系数c=0.6。因此,将判决前的信号表示为x=a+0.4n1+0.6n2。并且基于条件,从置信率角度来说,p(n1>n2)>p(n1 假设a=1:① 当n1和n2同为正号时,将x判决为1的置信率较高,此时判决正确。② 当n1和n2同为负号时,进行加权后,在Eb/N0较大的情况下,x<0的概率极低。因此,即使出现了n1和n2其中一个小于-1的情况,在和另一个加权后,会削弱较强噪声带来的影响,加权后x的值也会有一定的概率大于0。③ 当n1和n2异号时,同时有p(n1>n2)>p(n1 当a=-1时,与a=1的情况是对称的,因此不在此讨论。对于以上3种情况的讨论,在|n1|和|n2|不变的情况下,对判决影响最大的是情况②。不难得出,在n1和n2都不为0时,发生n1和n2同为负号的概率为1/4。 2.1.2 衰落信道 衰落是指信号强度随时间的变化,由于接收信号是通过天线接收从远端的发射机发出的,所以变化是在发送方与接收方之间的通信信道中产生的。在接收信号含有直达分量时,信号幅度衰落呈现莱斯分布,反之,信道幅度衰落服从瑞利分布[21]。其概率密度函数为: (30) 本文主要研究的是瑞利信道,信道模型如图3所示。 图3 瑞利信道模型Fig.3 Rayleigh channel model 图3中,xk,yk分别为信道输入及输出信号;nk为服从N(0,σ2)的信道高斯白噪声;rk为信道衰落系数,与时间具有相关性,因此该信道模型可表示为: yk=rkxk+nk。 (31) (32) 衰落通常分为快衰落和慢衰落2种: (1) 快衰落 幅度变化随着频率变化很快,快衰落起因于多路径引起的相消干涉,多普勒扩展导致频率扩散和时间选择性衰落[22]。 (2) 慢衰落 它不会随着频率变化很快。它的产生受机动性的影响,是由阴影和障碍物(如树木或建筑物等)引起的信号路径变化的结果[23]。 系统模型采用方案如图4所示。 图4 RS码的中继协作方案图Fig.4 RS code relay cooperation scheme 2.2.1 分布式RS码编码 1.1小节中论述了RS码的编码,对于源节点,φ(x)要编码的信息,其中生成多项式如式(1)所示。信息进行编码后得到码字c(x),将c(x)分别发送给中继节点和目的节点。在中继节点接收到来自源节点的信号解调判决后得到码多项式c′(x),使用Berlekamp译码后得到消息多项式φ′(x),并将译码后的信息重新编码得到码字多项式c″(x) ,调制后发送至目的节点。 例1:设α为GF(26)的本原元,该域是使用如下的本原多项式进行构造: q(x)=1+x+x6。 (33) 考虑码长为63个符号,信息长度为51个符号,最小距离为13的RS(63,51)码,符号取自GF(26)。其生成多项式有6个连续根,依次为α,α2,α3,α4,α5,α6,所以生成多项式为: h(x)=(x+α)(x+α2)(x+α3)(x+α4) (x+α5)(x+α6)。 (34) 1.1小节中论述了RS码的编码原理,使用式(34)中的生成多项式即可编码。 ① 首先将消息比特ω1映射为GF(26) 中的符号,映射后得到消息多项式φ(x)=φ0+φ1x+φ2x2+…+φ50x50,通过RS(63,51)编码器编码后得到码多项式c(x)=c0+c1x+c2x2+…+c61x61+c62x62,然后经过64-QAM调制后,发送至目的节点和中继节点。 2.2.2 联合译码算法 目的节点接收到来自源节点的幅值多项式θ(x)和来自于中继节点的幅值多项式μ(x)之后,对2个多项式相同的位进行带权值的加法运算,得到幅值多项式r(x)。将r(x)送入判决器之后得到码字多项式s(x),对s(x)进行联合译码后得到消息多项式φ″(x)。 例2:目的节点接收到来自源节点的幅值多项式θ(x)=θ0+θ1X+θ2X2+…+θ61X61+θ62X62,θi为复数,0≤i≤62。收到来自中继节点[17]的幅值多项式μ(x)=μ0+μ1x+μ2x2+…+μ61x61+μ62x62,μj也为复数,0≤j≤62。对每一符号位的值进行带有权值(Coefficient)的加法。 为了方便说明,在64-QAM中取点a和点b。其中点a=0.304 1-3.445 4i,b=0.682 6-2.867 3i,c=0.4a+0.6b。a,b,c在星座图中的位置如图5所示,图中横坐标为同相振幅,纵坐标为正交振幅。 图5 64-QAM星座图中的权重分配示例Fig.5 Example of weight assignment in a 64-QAM constellation diagram 假设r(x)为相加后的幅值信号,设权重系数为0.6,则r(x)的值如式(35)所示: r(x)=(0.6μ0+0.4θ0)+(0.6μ1+0.4θ1)x+…+ (0.6μ61+0.4θ61)x61+(0.6μ62+0.4θ62)x62= r0+r1x+r2x2+…+r62x62。 (35) 在仿真中,假设从源节点到中继节点之间的SNR=∞,仅考虑从中继节点到目的节点之间的差异性影响。 之前介绍了RS(63,51) 码的编码,为探究在不同信道条件下,权值加法系数对码性能的影响,加入RS(255,239) 码进行参照对比。 设β为GF(28)的本原元,该域使用如下的本原多项式进行构造: p(x)=1+x2+x3+x4+x8。 (36) 考虑码长为255个符号,信息长度为239个符号,最小距离为17的RS(255,239)码,所有符号取自GF(28)。其生成多项式有8个连续根,依次为β,β2,β3,β4,β5,β6,β7,β8,所以生成多项式为: h(x)=(x+β)(x+β2)(x+β3)(x+β4)(x+β5) (x+β6)(x+β7)(x+β8)。 (37) 1.1小节中论述了RS码的编码原理,使用式(37)中的生成多项式即可编码。 其中第一组为RS(63,51) 码和RS(255,239) 码在AWGN信道下的仿真结果,由图6可知,在源节点到中继节点信道完美,且在SNR(r,d)=SNR(s,d)+2 时,对于码RS(63,51),最佳权值系数(Coefficient)c=0.6(注:这里的量化单位精度到小数点后1位,即量化间隔最低0.1,经实验证实,0.01的单位精度下,系数之间的性能差异性不是很大。所以通过沿着(Eb/N0)从小往大并从大往小两侧逼近的方式,找到精度为0.1的最佳系数)。误码率在10-6时,相比于非协作通信,c= 0.6的方案大约有4 dBs的增益。 图6 采用权重协作方案的分布式RS(63,51)通过AWGN信道的BER性能曲线,编码率r=51/126 Fig.6 BER performance curve of distributed RS (63,51) using weight cooperation scheme over AWGN channel,coding rate r=51/126 考虑码RS(255,239) 在AWGN信道下的协作表现,图7采用和图6中一样信道条件进行仿真对比,显而易见,c=0.6 依旧是在SNR(r,d)=SNR(s,d)+2信道条件下的最佳系数。可知,在AWGN信道下,权值分配方案在协作通信中具有较好的性能表现。 图7 采用权重协作方案的分布式RS(255,239)通过AWGN信道的BER性能曲线,编码率r=51/126 Fig.7 BER performance curve of distributed RS (255,239) using weight cooperation scheme over AWGN channel,coding rate r=51/126 图8是在快衰落信道下的表现。在SNR(r,d)=SNR(s,d)+2 的信道条件下,在25 dB之后,各协作方案的BER曲线都有了大幅下降。系数c=0.6的协作方案的误码率是要略低于c=0.7的协作方案,是性能最优的方案,且性能差异较为明显。系数c=0.6的协作方案,相对于非协作方案来说,误码率在10-6时,大约有5 dBs的性能增益。 图8 采用权重协作方案的分布式RS(255,239)通过快衰落信道的BER性能表现,编码率r=239/510Fig.8 BER performance of distributed RS (255,239) using weight cooperation scheme over fast fading channel,coding rate r=239/510 提出了分布式RS码的中继协作系统和基于权重分配的译码算法,研究了2种信道条件下的性能表现。对于RS(63,51)和RS(255,239)来说,该方案带来的性能增益显著,不过在特定情况下,不同协作系数的性能差异不明显。除了文中提到的情况外的系数选择,需要通过实验中逐渐逼近的方式得到。该方案加入MIMO之后的性能增益和不同MIMO带来的性能差异,是之后的研究方向。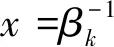
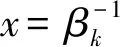
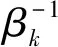
2 分布式RS码中继协作系统的构造
2.1 信道模型
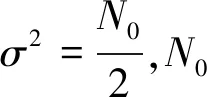

2.2 系统模型
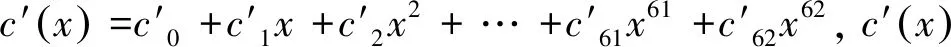
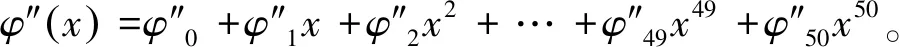
3 仿真结果与分析
4 结束语

