基于自适应权重Retinex和小波变换的彩色图像增强算法

冯红波，李 萍，王 博

(宁夏大学 物理与电子电气工程学院，宁夏 银川 750021)

0 引言

非均匀环境光照射的图像通常具有低全局对比度和小灰度分布，这会导致暗区的内容模糊和细节丢失。此外，由于不均匀光线所造成的局部过度曝光或欠曝光会严重限制图像分析系统和设备的性能。因此，应增强图像暗部区域的细节，抑制过度曝光，增强欠曝光，改善全局对比度和动态范围来恢复此类图像。

当前，常用的图像增强算法包括直方图均衡化(HE)算法[1]、小波变换[2]、Retinex算法[3]和图像融合[4]等。其中，小波变换算法是将图像从空间域换到小波域分解为高频图像和低频图像，使用各种增强算法对图像进行增强，实现对比度和细节增强[4]。图像融合的增强算法主要是将不同图像中人们感兴趣的特征提取出来进行综合得到质量更高、视觉较好的图像[5]。另一个表现比较出色的算法就是基于Retinex[3]算法，例如单尺度Retinex(Single Scale Retinex，SSR)[6]、多尺度Retinex(multi scale Retinex，MSR)[7]以及带色彩恢复的多尺度Retinex(Multi Scale Retinex with Color Restoration，MSRCR)[8]等。近些年学者们对Retinex算法进行了深入研究，提出了许多改进的算法。Gabriele Gianini[9]等人提出了基于马尔可夫链的Retinex图像增强模型。同年，常戬[10]等提出一种基于回转对称双边滤波的Retinex图像增强算法，采用回转对称双边滤波进行光照估计，增强后的图像视觉效果表现良好。石磊[11]等提出了一种可控核函数双边滤波Retinex水下图像增强算法，该算法通过可控核函数的双边滤波对光照分量进行估计，有效解决了边缘模糊现象。Shu Zhang[12]使用改进的MSR算法对水下图像进行增强，并利用双边滤波与三边滤波结合的方式对彩色图像进行滤波。卢玮[13]等提出了一种利用Retinex与融合思想结合的彩色图像增强算法，主要解决光晕现象与过增强。Retinex算法是基于光照均匀条件下的增强算法，对于光照不均图像，Retinex算法虽然能够增强图像的亮度和对比度，但是存在色彩失真现象，MSR算法是SSR算法在3个尺度下的加权平均，色彩得到改善，但仍存在失真现象。

针对以上算法存在的问题，提出了一种基于自适应权重的多尺度Retinex +(Adaptive weighted multi scale Retinex，AMSR)和小波变换(Wavelet Transform，WT)结合的图像增强算法(AMSR-WT)。通过自适应权重代替平均权重，在HIS空间中对亮度分量I进行AMSR-WT算法增强。实验结果表明，该算法增强效果明显，色彩保真度高且有细节。

1 Retinex算法原理及存在的问题

1.1 Retinex算法原理

Retinex理论是LAND E H[3]提出的基于色彩恒常的色彩计算理论。该理论认为在光照均匀条件下，图像S(x，y)是由反射分量R(x，y)与照射分量L(x，y)组成：

S(x，y)=R(x，y)·L(x，y)，

(1)

式中，R(x，y)包含了图像的内在属性；L(x，y)包含了图像的动态范围。常见的使用高斯滤波来估计照射分量：

L(x，y)=F(x，y)*S(x，y)，

(2)

式中，*为卷积运算；F(x，y)为高斯滤波函数，定义为：

(3)

式中，c为高斯尺度；λ令F(x，y)积分和为1。

将式(1)～式(3)转换到对数域可得：

r(x，y)=lnR(x，y)=

lnS(x，y)-ln[F(x，y)*S(x，y)]，

(4)

式中，r(x，y)为最后的增强图像。

1.2 Retinex算法存在的问题

经典的MSR算法是SSR算法的延伸，它结合了小尺度、中尺度和大尺度的优点，既实现了动态压缩，又实现了色调还原。一般情况下，小尺度算法会以色彩欠饱和以及光晕为代价实现图像增强；大尺度算法可以在不改变全局对比度的条件下实现图像的色调还原，但仍存在部分失真；而中等尺度则为大尺度和小尺度之间的折中算法。MSR 增强模型可以表示为：

(5)

式中，N为尺度个数，一般N=3；ωn为权重占比，一般使用平均权重：

(6)

由于不同尺度的Retinex算法在明暗区域具有不同的增强效果，在加权求和时也应具有不同的权重值，而不应该一概而论地使用平均权重。图1为一幅RGB图像分别使用小中大三尺度(15，80，250)增强后的结果。

(a)原图

(b)小尺度增强图

(c)中尺度增强图

(d)大尺度增强图

由图1(b)可以看出，小尺度增加了局部对比度，但是色调变差，如天空的颜色出现失真，并且建筑边缘出现光晕；由图1(d)可看出，大尺度算法可以很好地保留亮度区域与暗度区域的整体色调；图1(c)为大小尺寸的折中表现。

2 AMSR算法增强模型

由1.2小节可知，对于亮度区域和暗度区域，大尺度的SSR算法是优选，因此大尺度SSR的权重占比大，小尺度和中尺度SSR占比小。权重的获取需依据原图的像素值。首先将图像中的像素平均分为4种类型，即暗像素点、中暗像素点、中亮像素点和亮像素点。在[0，255]范围内利用标准正态分布代表，参数为：

(7)

正态分布结果如图2所示。

图2 正态分布结果Fig.2 Normal distribution results

对原图像的4类像素点分别计算似然概率，其中中间2类(中暗、中亮)作为一类像素点进行计算，则有：

p1(x，y)=e-(I(x，y)-μ1)2/2σ12，

(8)

p2(x，y)=e-(I(x，y)-μ2)2/2σ22，

(9)

p3(x，y)=max{e-(I(x，y)-μ0)2/2σ02，e-(I(x，y)-μ3)2/2σ32}。

(10)

p1(x，y)，p2(x，y)，p3(x，y)分别对应小尺度、中尺度和大尺度的概率值。

为了能够得到原图像的权重，定义p0(x，y)=1。根据这些概率值，原图像与3个尺度的SSR算法的权重定义为：

(11)

原图以及3个尺度下每一个像素点的权重如图3所示。

的权重

的权重

的权重

(d)原图的权重

由图3(a)可以看出，对于小尺度SSR增强图像在边缘部分亮度大，具有较大的权重值，在其他地方亮度低，具有较小的权重值；图3(c)中，对于大尺度SSR增强图像在黑暗和明亮区域亮度大，具有较大的权重值，在边缘处亮度低，具有较小的权重值。

依据原图得到的自适应权重值与SSR增强结果进行加权求和即得到最后的增强图像：

(12)

3 AMSR-WT算法

3.1 颜色空间转换

考虑到Retinex算法在RGB空间进行图像增强会使颜色趋于灰色，且RGB空间的图像在红、黄和蓝3个通道存在相关性。HSI空间更与人眼视觉观察图像相近。因此将图像从RGB空间转换到HSI空间，色调分量H与饱和度S和亮度分量I相互分离，仅对亮度分量I进行处理。

对于一张RGB图像，将其归一化到(0，1)，I，H，S定义为：

(13)

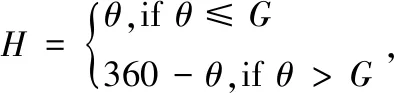
(14)

式中，θ定义为：

(15)

(16)

从HIS空间到RGB空间的转换：

H=2πH。

(17)

若H∈[0，2π/3)，则：

(18)

若H∈[2π/3，4π/3]，则：

(19)

若H∈[4π/3，2π]，则：

(20)

图4为一幅图像的HSI空间图以及各分量图。

(a)H分量

(b)S分量

(c)I分量

(d)HSI空间图像

3.2 小波变换

WT是通过一系列的小波函数族去表示某一信号。小波函数族可以定义为[14]：

(21)

式中，j0为开始尺度；cj0(k)为尺度度系数；dj(k)为小波系数。

数字图像作为二维离散信号可以通到离散小波变换(DWT)进行分解为低频系数和高频系数，低频系数图像主要是图像的平滑区域，高频系数包括图像的细节轮廓[15]。本文使用‘sym4’小波函数族对I分量图像进行一级小波变换分解为1个低频系数和3个高频系数(垂直、水平和对角线)，示例如图5所示。

(a)近似分量

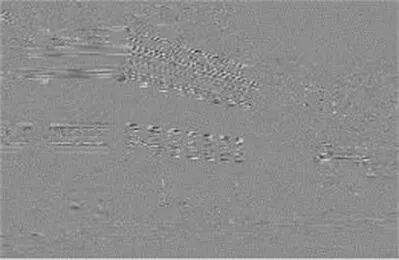
(b)水平分量

(c)垂直分量

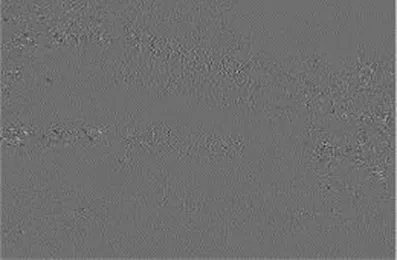
(d)对角线分量

通过离散小波变换得到的近似分量可理解为图像的近似表示。亮度分量I经过小波变换后分解得到近似分量，然后利用AMSR算法进行增强，增强结果如图6所示。

(a)近似分量

(b)近似分量增强

从图6可以看出，原图的对比度以及亮度得到明显提升。

3.2 高频系数去噪

本文采用小波阈值去噪算法对高频系数进行处理。阈值估计采用固定阈值估计法：

(22)

式中，λ为固定阈值；σ为噪声标准差；median()为中值函数。

本文采用的是文献[16]的渐近软阈值函数。计算表达式为：

(23)

将去噪后的高频系数与增强后的低频图像通过小波逆变换得到增强的亮度分量I_enh，最后利用gamma校正进一步增强对比度。图像从HIS空间转换回RGB空间得到最后的增强彩色图像：

I_enh`(x，y)=(I_enh)1/γ，γ∈[1，+∞)。

(24)

4 实验分析

本文选取3幅图像用本文算法进行实验仿真，并与HE，MSR和MSRCR算法进行结果对比。算法仿真环境：Intel(R)Core(TM)i5-8400 CPU@2.80 GHz，操作系统：Windows10，软件环境：python3.6。参数设定：小波基：‘sym4’，λ1=15，λ2=80，λ3=250，G=5，b=25，a=125，β=46。

图7～图9为3幅图像的仿真结果。以图7的结果对比图为例，可看出4种算法在对比度和亮度上都有明显提升，但是前3种算法出现了明显的色彩失真现象：图7(b)中的天空部分因过增强而颜色失真，且建筑边缘细节模糊；图7 (c)和图7 (d)整体颜色偏向灰色，且局部出现严重色彩失真(如天空，本为晴天，增强后为阴天);图7 (e)无色彩失真现象，细节提升明显，亮度与对比度增强不存在过增强和欠增强，整体视觉效果良好。图(8)与图(9)可以得出同样的结果，因此本文提出的AMSR-WT算法优于其他3种经典算法。

(a)原图

(b)HE增强结果

(c)MSR增强结果

(d)MSRCR增强结果

(e)AMSR-WT增强结果图7 建筑物增强结果对比Fig.7 Comparison of building enhancement results

(a)原图

(b)HE增强结果

(c)MSR增强结果

(d)MSRCR增强结果

(e)AMSR-WT增强结果图8 室内人物增强结果对比Fig.8 Comparison of indoor character enhancement results

(a)原图

(b)HE增强结果

(c)MSR增强结果

(d)MSRCR增强结果

(e)AMSR-WT增强结果图9 室内物体增强结果对比Fig.9 Comparison of indoor object enhancement results

人眼主观评价是评判图像增强算法的一个重要标准，但为了进一步说明所提出增强算法的效果，通过计算对比度、信噪比、信息熵和算法时间进行比较。图像越清晰对比度越高；信噪比为图像信息量与所含噪声的比值；信息熵反映图像信息的丰富程度；算法时间反映算法实时性的强弱。结果如表1～表3所示。

表1～表3的仿真数据表明，本文算法AMSR-WT在3幅实验图像增强结果中，绝大多数指标均优于其他算法。对比度最高表明图像最清晰，信噪比优于其他算法说明降噪明显，信息熵最优，表明拥有更多的信息量和呈现更多的图像细节。算法时间由于算法复杂度略高于其他算法。

表1 建筑图像质量评价对比
Tab.1 Comparison of architectural image quality evaluation

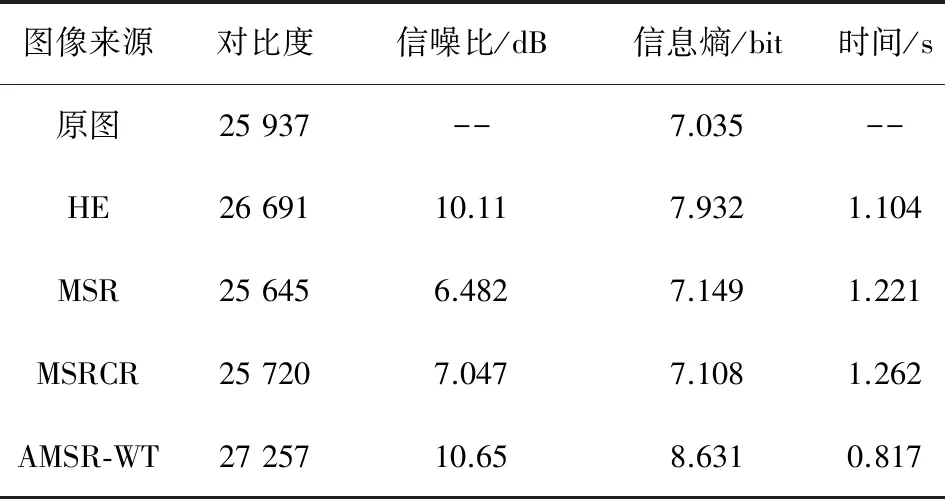
图像来源对比度信噪比/dB信息熵/bit时间/s原图25 937--7.035--HE26 69110.117.9321.104MSR25 6456.4827.1491.221MSRCR25 7207.0477.1081.262AMSR-WT27 25710.658.6310.817

表2 人物图像质量评价对比
Tab.2 Comparison of character image quality evaluation

图像来源对比度信噪比/dB信息熵/bit时间/s原图21 365--7.301--HE23 14816.217.4940.212MSR21 5628.3737.0870.878MSRCR21 6118.7817.0770.899AMSR-WT23 25817.057.6390.892

表3 室内图像质量评价对比
Tab.3 Comparison of indoor image quality evaluation

图像来源对比度信噪比/dB信息熵/bit时间/s原图15 109--5.34--HE15 4496.097.240.474MSR17 7916.816.811.350MSRCR17 7417.027.161.620AMSR-WT19 30511.027.270.703

5 结束语

针对光照不均彩色图像增强过程中细节丢失、色彩失真和扩大噪声等问题，本文提出了基于小波变换与自适应权重Retinex的单张彩色图像增强算法(AMSR-WT)。选取3幅图像，通过python进行仿真并与3种经典增强算法进行对比，结果表明本文算法在人眼主观评价、客观数据评价上具有明显优势，但是算法运行时间较长，下一步将对算法进行优化，降低算法的复杂度，减少算法的运行时间，提高本文算法的实时性。