那些年我们追过的江苏卷上的热点——兼谈对高考真题研究的思考

卞康林 (江苏省溧阳市戴埠高级中学 213300)

2020年高考落下了帷幕，江苏高考自主命题也完成了它的历史使命．尽管江苏卷大多数时候给人的印象是难度很大、要求较高，但不可否认的是，江苏卷的命制一直维持在较高的水准，既侧重考查考生的基本数学能力和数学核心素养，又能引导考生对数学思想的追寻和数学应用的探索．尤其是从2008年起，江苏卷自成一格，试题也是自带热点，每年都会有一些设计精妙、蕴含一定数学思想的试题引起众多专家及师生的热议和关注，试题本身所涉及的数学原理、思想方法、知识背景，以及典型的解法都会引起广泛的研究和讨论，也会在很大程度上成为下一年备考的热点题型，由此产生了高考热点问题的模型化、结论化、题海化等现象．本文通过对部分江苏卷上典型的热点问题进行回顾，对上述现象进行一定的剖析和思考，同时向曾经带给我们无数痛苦、快乐、深思的江苏卷致敬．

1 那些年我们追过的热点

热点1 有一种图形叫隐形圆

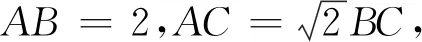
此题一出，接下来的每一届高三学生都知道了阿波罗尼斯圆，更进一步，大家都在研究哪些方程形式可以化归为圆的方程，真是初见不识圆，再看处处圆，隐形圆从此名声大噪．事实上，此题完全可以从解三角形的角度表示出面积关于边长或角的函数来求解，相比隐形圆的角度，我们可以理解为平面几何与解析几何的碰撞，解析几何的角度赋予了图形的动态直观，体现了方程与曲线的互相转化，也就是可以从数形结合的角度进行理解．此外，可用隐形圆的角度解决的高考试题多次出现过，如2013年第17题，2017年第13题．

热点2 第一定义、第二定义，还有第三定义

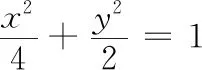
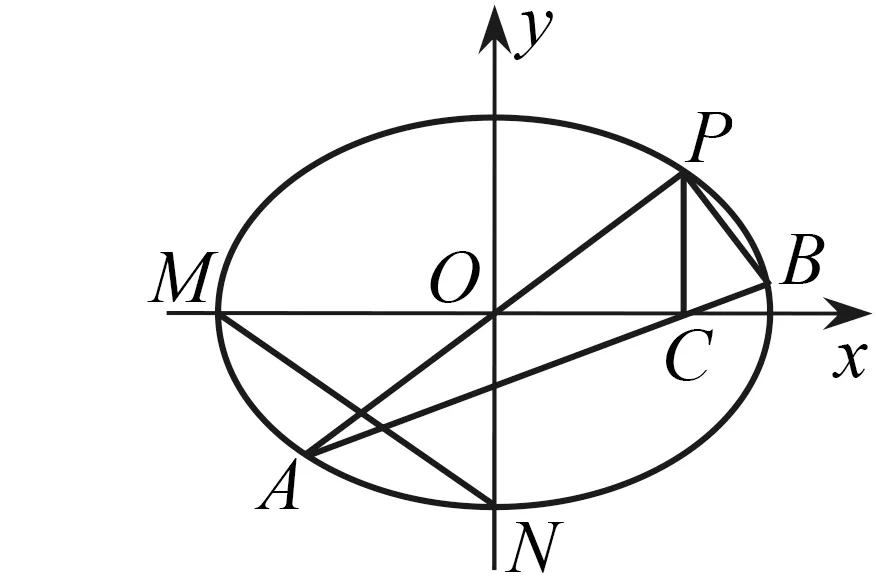
图1

(1)(2)略；(3)对任意k>0，求证：PA⊥PB．

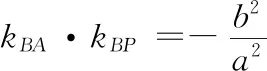
热点3 有一种数量积的解法叫极化恒等式

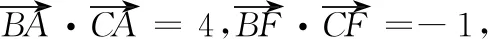
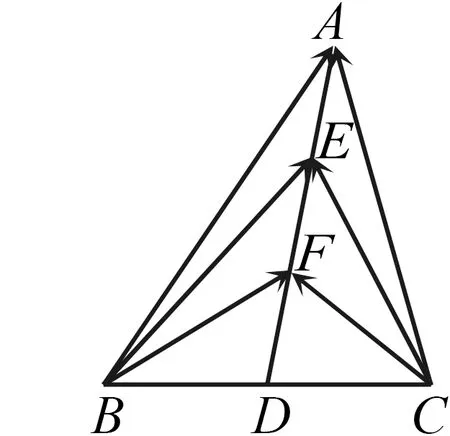
图2

作为一道考查向量数量积的高考试题来讲，从基底法或坐标化的角度来解决并不复杂，从极化恒等式的角度来说，更高效，无论哪种方法都能很好地体现方程思想．我们发现，当已知条件集中在三角形的中线和对边、继而考查向量数量积的时候，极化恒等式的效果是比较明显的．但是，在教学过程中，一些教师过于神话这一方法，而忽视了这一方法的本质依然是基底法，只不过是选择了两个特殊的向量作为基底．这就说明，我们在研究高考题时，不要机械地停留在某些方法的表面，不要将其神话，而应该发掘试题背后的数学思想，探究其本质，从而进一步加深对通性通法的理解．

热点4 定点、定值的热度从未减退

典型试题(2008·江苏18)在平面直角坐标系xOy中，设二次函数f(x)=x2+2x+b(x∈R)与两坐标轴有三个交点，经过三个交点的圆记为C．

(1)(2)略；(3)问圆C是否经过定点(其坐标与b的值无关)？请证明你的结论．

凡是高三学生复习到解析几何的内容，定点、定值问题是无法回避的．这类问题综合程度高，涉及到的通性通法多，复习价值大．此题的常规解法为将图形过定点的几何特征转化为方程恒成立(与参数无关)的代数关系．此后，2009年第18题、2010年第18题均考查了定点问题，2011年第18题(第3问证明题，本质上是求证两直线斜率乘积为定值)、2012年第19题均考查了定值问题．

热点5 不会“取点”是无法驾驭“零点存在性定理”的

典型试题(2013·江苏20)设函数f(x)=lnx-ax，g(x)=ex-ax，其中a为实数．

(1)略；(2)若g(x)在(-1,+∞)上是单调增函数，试求f(x)的零点个数，并证明你的结论．

江苏卷对函数的零点的考查频率是很高的．回头来看此题中的两个函数，是现在研究运用零点存在性定理解决函数零点问题最常见的两个函数模型，由此可见此题的经典非同一般．两个函数中汇集了指数函数、对数函数、一次函数，这似乎在告诉我们，弄清楚不同函数的变化率就可以判断清楚由它们组合而成的新函数的变化趋势，加上一些适当的放缩，就可以取得一些能够使得函数值为正或负的合适的点．对于学生来说，如果对于一些常见函数的性质理解不到位，就会对取点的方法把握不好，导致不能解决问题．不得不说的是，对函数零点的考查，重点还是应用零点存在性定理研究零点的个数及分布，“取点”只是其中的一个要素，怎样取到合适、“好看”的点只是小技巧，不能一叶障目，不见泰山．

江苏自主命题一路走来，热点远远不止以上所列的几个.中学教师对高考真题向来是相当重视的，历年来的研究也是成果丰硕．然而，如何从高考热点真题中汲取营养，既提高个人的数学素养，又高屋建瓴、更加合理地服务于学生对数学学习的需求，提高学生的核心素养，就不仅仅是几个研究的小成果能解决的了．

2 对高考热点试题研究的思考

对高考真题的研究一般都会深入探究其内涵及其外延，即前面所提到的数学原理、思想方法、知识背景，以及典型的解法等，主要目标是弄清高考考什么，怎样备考更有针对性、更高效．对试题内涵的探究能够帮助我们更好地理解高考的考查方向，加深对知识本身的感悟，更好地串联起题型与方法之间的联系．很多模考试题都改编自高考题，通过对高考真题的提炼、重组，形成新的问题情境，不难看出对高考题深入研究的重要性．

在具体实践中，我们也容易发现有一些用力过猛、提炼不当的情况.

(1)贴标签式的专题复习

以热点3为例，在一些复习资料中，将大量适用极化恒等式解决的向量问题进行罗列，忽略审题，不分析解题目标，通篇地套公式，题目做得很多，产生思维定势，甚至原本可以轻松地用基底法或坐标法解决的问题，也变得“不识庐山真面目”．如何解决这样的问题呢？笔者认为，某个方法的提炼一定有其合理性，关键是教学过程中要阐述清楚为什么这个方法更高效(寻找数学原理、思想方法)，对用来做巩固的练习要精选，量少而精(体现知识背景)，从引导学生“就这么做”到“为什么这么做”，从方法体系的扩充到数学思想的完善，从而提高学生的数学素养．

(2)过于强调二级结论

在对高考真题知识背景的研究过程中，很容易引出一些二级结论．以热点2为例，引出椭圆的第三定义是比较自然的，但我们一些教师过于强调二级结论，盲目地补充，要求学生识记，本末倒置．一方面，我们发现，高考考查从来都不会依赖所谓的二级结论才能解决，高考试题一大特点是来源于课本、以本为本，因此，考查的重心一定是通性通法；另一方面，我们可以更加关注二级结论的推导、形成过程，追根溯源，才能更好地理解问题的本质．

3 结束语

江苏考生将从2021年起迎来全国卷，一些教师认为研究江苏卷已经失去了实际意义，从前面的论述不难看出，如果定位是曾经的江苏卷上出现的某个具体的方法、具体的某个知识点与全国卷的对应关系，确实我们很难有太多收获．因为，那些从未改变的是我们在学习和探索的过程中所认识到的深刻的数学思想、缜密的解题逻辑、精巧的解题策略．我们认识到从“维纳斯身高”到“埃及胡夫金字塔”的题目实为异曲同工，对学生核心素养的考查从未曾改变．