在教学设计细节中体悟“数学味”

黄厚忠 (江苏省镇江市教育科学研究中心 212008)

刘新春 (江苏省扬中市教师发展中心 212200)

在平时的教学研究活动中，广大教师通过听课、说课、议课等形式加深对数学教学内容、课堂教学设计和教学策略方法的理解，同时进一步提升自身的学科素养和教学素养．但我们也发现，部分教师在课堂教学设计中只重视教学总目标和教学结构的设计，缺乏对教学细节的琢磨，缺少了一点“数学味”，导致数学核心素养像天上的云到处飘，无法扎根.数学核心素养的培养应渗透在具体的教学细节之中，教师不仅要仰望星空瞄准大目标，更要关注细节，对每一个教学行为、每一个知识点，甚至是学生的每一个带有疑问的眼神进行思考分析，寻找实现教学目标的生长点．本文以“椭圆的标准方程”的教学设计细节为例谈谈如何思考细节，自然、合理、严谨地呈现数学的“原汁原味”．

“椭圆的标准方程”主要内容是从椭圆的定义出发，类比圆的方程的推导，通过建立恰当的直角坐标系，表示椭圆上点的坐标满足的数量关系——方程，合理化简推导椭圆的标准方程，研究椭圆的基本性质．在本节内容的教学过程中有许多细节值得推敲，教师的精心设计可以更好地展示数学的本质和魅力，教出一些“数学味”来，也有利于学生更好地理解数学本质，学习自然、优美、透彻的数学．现就本节课的教学细节结合平时教师上课、说课的状况提出一些思考．

思考1为什么设椭圆的两焦点F1,F2之间的距离为2c，椭圆上任一点P到F1,F2的距离之和为2a(2a>2c)，而不设F1F2=c，PF1+PF2=a？

许多教师认为这仅仅是为了运算方便，不需要让学生知道理由．其实这样的假设至少可以从以下四方面阐述理由：一是建立坐标系后设点方便，避免了用分数表示点的坐标(前提是按标准方程建系)；二是化简方程时由于根号里均为整式无分数，运算方便；三是a,b,c的几何意义明晰；四是最终的椭圆方程的形式最简单，便于通过标准方程研究椭圆的基本性质.如若在推导了标准方程后提出假设F1F2=c，PF1+PF2=a，把设点的坐标、化简方程、方程的最后形式与标准方程比较，让学生自己体会如何合理、简洁地进行运算．在推导双曲线的标准方程时，学生就会自然而然地想到如何设焦距和实轴长.但是在推导抛物线的标准方程时为什么设焦点到准线的距离为p而不是2p呢？这是因为尽管设为p但抛物线方程的化简形式并不复杂，而且其结果y2=2px(p>0)已经是整系数形式，如若设焦点到准线的距离为2p，则标准方程为y2=4px(p>0)，系数反而增大，不符合简单精炼的原则．

抓住这一问题，以小见大，讲清道理，学生可以知道数学中的假设是合理的、表达是明白的、结果是简捷的．

思考2为什么以椭圆的两焦点F1,F2所在直线为x轴，以线段F1F2的垂直平分线为y轴建立直角坐标系？

从圆的方程的几种形式中我们知道，圆在坐标系中的位置不同，圆的方程的形式也不相同，圆的最简方程是圆心在原点、半径为R的方程，即x2+y2=R2．椭圆的方程有没有最简形式呢？如有，要找到椭圆的最简单的方程形式，就要建立恰当的直角坐标系，就要遵循简单、方便、美观等原则，便于用最少的字母和最简单的形式表示点的坐标和曲线方程．对椭圆来说，一开始就由圆心类比椭圆中心并不恰当，但反向思考，如若以一个焦点为原点建立直角坐标系，则直观感觉两焦点不对称、不和谐．因此，从焦点的对称性来看，以两焦点的中点为原点较好．

对于整式方程来说，如果曲线图形关于x轴对称，则曲线方程不含有y的奇次项；如果图形关于y轴对称，则方程不含有关于x的奇次项；如果曲线同时关于x轴、y轴对称，则方程既不含有x的一次项又不含有y的一次项；如果曲线经过原点，则方程不含有常数项．对于椭圆来说，直觉认为它是匀称的，这为我们建系提供了感性帮助．

这样的建系方法对于双曲线来说同样是简单的，在建立抛物线的标准方程时也可以再次得到验证．

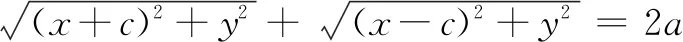
怎样想到要化简的？这既是直觉(因为形式繁、有根式)又是愿望，直线和圆的方程的形式都比较简单，不含有根式，我们当然希望椭圆的方程也比较简单.化简方程首要的问题是如何去掉根号，许多教师为了节省时间直奔主题，直接告诉学生移一个根号到另一边平方化简．如果稍加思考，就会产生许多问题：不移项直接平方行不行？不平方行不行？等式两边平方与原等式是否等价变形？化简方程有哪些策略与方法？化简到什么程度才是最简形式？

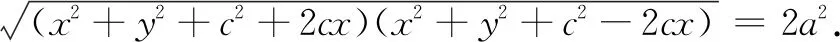
移项平方，由于等式两边都只含有一个根号，看起来比较平衡协调，平方后的项数较少，且次数最高为二次，便于化简，因而教科书采用了此法．

第二，根据数式化简的基本要求，尽量不含根号，项数尽可能少，不含有分式，并且与直线的截距式方程、圆的最简方程类比，不难获得化简方程的目标．如果先布置学生推导一个具体的椭圆方程，再启发学生与直线的截距式方程对比，则对于一般椭圆的标准方程的化简目标更加明确.数学讲推理但也要讲道理，步步有理、自然而然才是数学的本质．

第三，各种推导方法如何选用？是每种方法都讲，还是只讲一种方法？应该根据班级学生的实际和学生在推导过程中出现的方法和问题因势利导.首先立足于掌握教科书上的方法正确，这是最基本的要求，让所有学生既掌握一种推导方程的基本方法，又经历如何进行数式运算、如何采取相应的策略简化运算过程，在推导过程中提高数式运算和推理论证能力．如果学生基础较好，可把探究其他方法作为研究性课题交给学生思考交流．

思考4为什么假设a2-c2=b2？

此假设基于以下原因：

(1)a,c均为正数，且a>c，因而a2-c2>0，a2-c2表示一个正数．

(2)在方程中每一个字母的次数都是二次，如设a2-c2=t，则代入方程明显不协调，也不能准确表达t为正数的特性．

(3)a,c表示距离，b是否也有几何特征呢？这就很容易联想到直角三角形，结合图形OF2=c，PF1+PF2=2a，当PF1=PF2=a时，点P恰好是椭圆与y轴的交点，此时b就可以表示原点到上下顶点的距离．

(4)此假设使椭圆方程更加简单，还具有对称性，更便于研究椭圆的性质．

思考5为什么只要把焦点在x轴上的椭圆的标准方程中x,y交换位置就可以得到焦点在y轴上的椭圆的标准方程？

有的教师教学生猜焦点在x轴上的椭圆的标准方程，说这体现了归纳猜想的思想，这是不对的，这里没有用到归纳．还有教师说由椭圆的对称性，只需将x,y交换就可以得到焦点在y轴上的椭圆的标准方程，这种说法也不妥当，缺乏依据.猜想必须依据已有的事实，而依据椭圆的对称性并不恰当，因为推导椭圆方程的过程中并不知道椭圆的对称性，以下对比分析具有合理性．

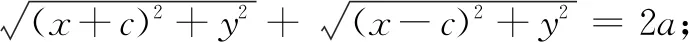
对比分析两式的差异，交换两式之一中x,y的位置就可以得到另一等式，因而猜测其结果可能是交换化简后的方程中x,y的位置可以得到另一个方程，但这并不能代替推导证明.数学讲究严谨，让学生自行推导，既进一步熟练了推导过程，又验证了自己的判断，可谓一举两得．

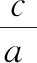
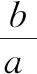
教师可从两个角度加以分析．

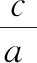
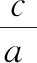
思考7为什么用椭圆的标准方程研究椭圆的性质？

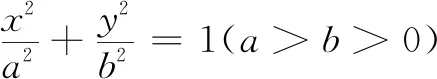
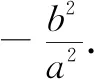
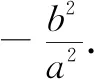
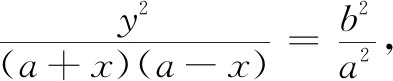
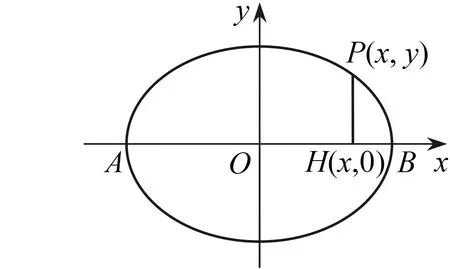
图1

思考8研究椭圆的标准方程及其性质用到哪些数学思想方法？

部分教师对本节内容中隐含的数学思想方法有所忽视，或知之甚少，或无意疏忽，其实解析几何是代数与几何的有机结合，是数形结合的经典范例，椭圆的标准方程的各种变形形式无不揭示着相应的几何性质．类比是解析几何研究问题的常用方法，本节内容中椭圆与圆的研究方法和性质的类比，后续内容双曲线与椭圆的方程、性质以及研究方法的类比，整个圆锥曲线知识的类比，无不渗透在每节课的教学之中．方程的思想更是贯穿解析几何教学始终．椭圆的标准方程的推导过程的等价转化思想、研究椭圆性质时方程的等价变形、解决与椭圆相关问题时解题过程中的等价转化思想随处可见．在课堂教学中举手投足皆思想，就看教师是否用心去体会、实践、显化．