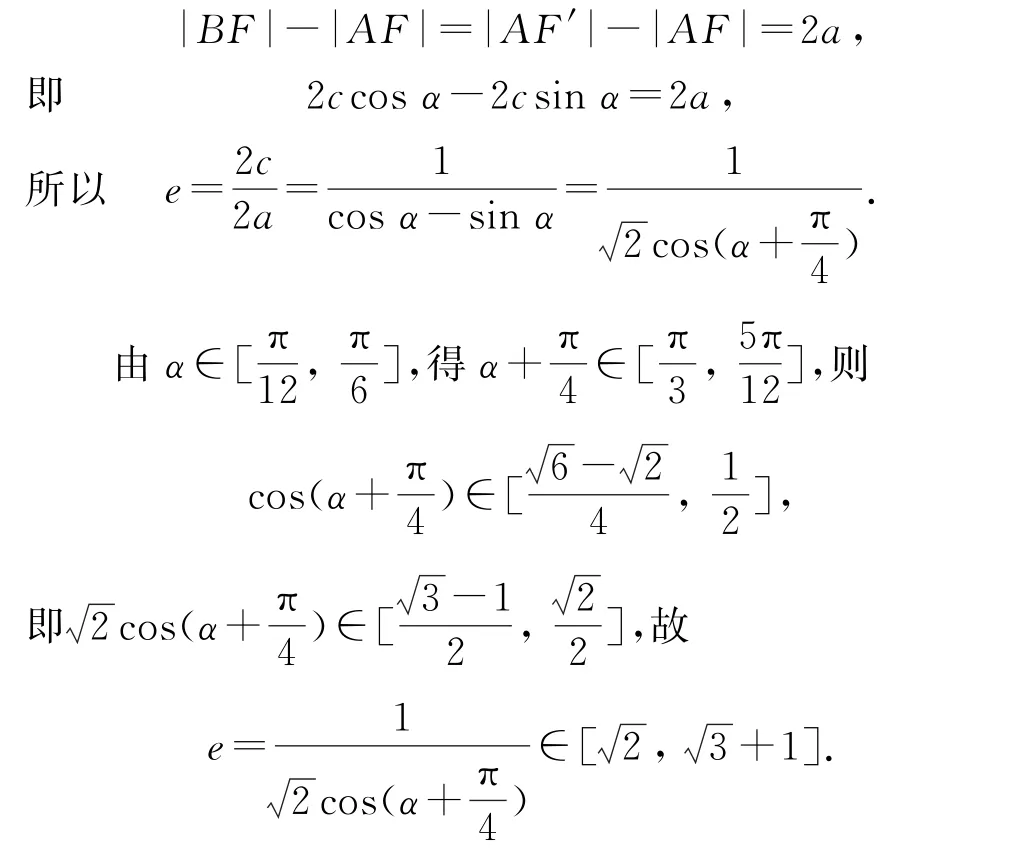求双曲线离心率的几种方法
◇ 河南 张振继(特级教师)
1 从离心率的定义出发考虑
已知双曲线的焦距及实轴的长分别为2c,2a,则其离心率.
例1已知双曲线的左、右焦点分别是F1,F2,过F1作圆x2+y2=a2的切线,切点为E,交双曲线右支于点P,若则双曲线C的离心率为_______.
解析

点评
本题通过题设条件求出a,c的值,然后再利用离心率的定义求得离心率.
2 从双曲线渐近线的斜率出发考虑
中心在原点O,焦点在x轴上的双曲线渐近线的斜率为k,则离心率.
中心在原点O,焦点在y轴上的双曲线渐近线的斜率为k,则离心率.
例2(1)已知抛物线x2=-4by的准线与双曲线的左、右支分别相交于B,C两点,A为双曲线的右顶点,O为坐标原点,若∠BOC=4∠AOC,则双曲线的离心率为________.
A.(1,2] B.(1,2)
C.[2,+∞) D.(2,+∞)
解析
(1)抛物线的准线方程为y=b,与双曲线方程联立,可得由∠BOC=4∠AOC,可得所 以 ∠AOC=30°,所以
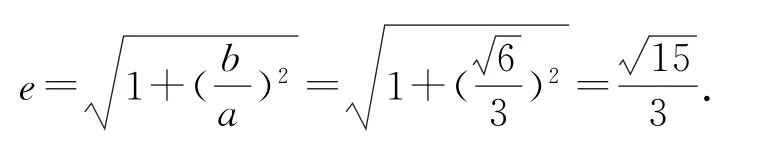
3 从双曲线的渐近线与实轴的夹角考虑
已知双曲线的渐近线与实轴的夹角为α,则其离心率.
例3(1)已知双曲线的左、右焦点分别为F1(-c,0),F2(c,0),圆x2+y2=c2与双曲线一条渐近线交于点A,若直线AF1与另一条渐近线的交点B恰好是AF1的中点,则双曲线的离心率为( ).
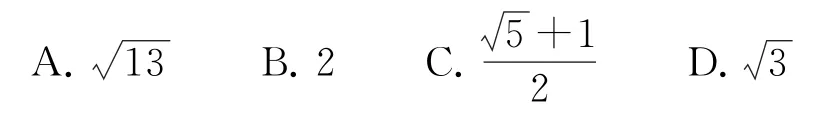

解析
(1)由题设,得F1A⊥AF2,B,O是分别是AF1,F1F2的中点,所以OB⊥AF1,故∠BOF1= ∠AOB.又 ∠AOF2= ∠BOF1,所 以∠AOF2=60°,离心率故选B.
(2)由题设|F1F2|=2c,∠F1AF2=90°,∠AF2F1=30°,所以 ∠AF1F2=60°,而|OF1|=|OA|,所以△AF1O为等边三角形,所以∠AOF1=60°,即其中一条渐近线的倾斜角为60°,故e=所以选A.
4 构建离心率e的方程
例4(1)(2019年全国卷Ⅱ文12)设F是双曲线的右焦点,O为坐标原点,以OF为直径的圆与圆x2+y2=a2相交于P,Q两点,若|PQ|=|OF|,则双曲线C的离心率为( ).
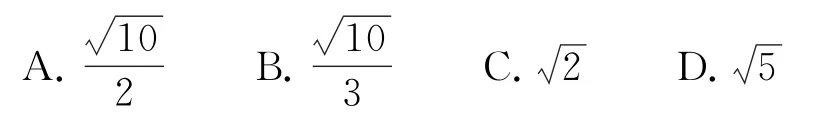
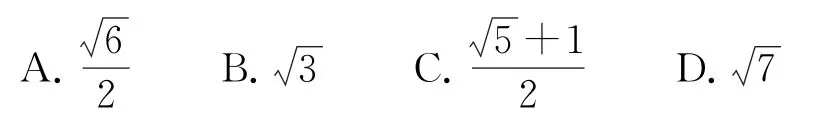
解析
(1)以OF为直径的圆的方程为两式相减得所以
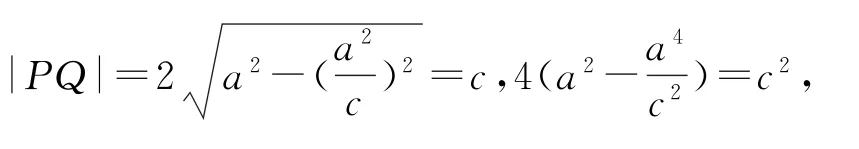
即e4-4e2+4=0,解得e2=2,所以,故选C.
(2)设△F2AB边长为t,由双曲线的定义,得|BF1|-|BF2|=2a,则|BF1|=2a+t,所以|AF1|=2a.
又|AF2|-|AF1|=2a,所以|AF2|=4a,在△AF1F2中,∠F1AF2=120°,|F1F2|=2c,由余弦定理,得(2c)2=(2a)2+(4a)2-2×2a·4acos120°,解得,即双曲线的离心率为7,故选D.
5 构建离心率e的不等式
例5已知双曲线的左、右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|=4|PF2|,则双曲线的离心率e的最大值为( ).

方法1利用|PF1|+|PF2|≥|F1F2|构造不等式.由双曲线定义,得|PF1|-|PF2|=2a,又|PF1|=4|PF2|,解得又.
方法2利用右支上的点的焦半径大于等于ca构造不等式.设右顶点为A,则|PF2|≥|F2A|,即.
方法3利用右支上的点的横坐标大于或等于a构造不等式.设P(x,y),则所以解得.
6 构建离心率e的函数
例6已知双曲线右支上有一点A,它关于原点的对称点为B,点F为双曲线的右焦点,AF⊥FB,∠ABF=α,且则双曲线C的离心率e的取值范围是________.
解析
设双曲线的左焦点为F′,连接AF′,BF′,则四边形AF′BF为矩形,故|AB|=|F′F|=2c.在 Rt△ABF中,|AF|=2csinα,|BF|=2ccosα.由双曲线的定义,得