例谈2020年高考圆锥曲线定义的应用
◇ 山东 苏丽娟
圆锥曲线的定义既是重要的数学概念,也是解答许多问题的重要工具,因此成为高考考查的重点.在解答问题时,若能灵活、巧妙地应用圆锥曲线的定义,就能深化对圆锥曲线概念的理解,同时还能提高运用定义去分析和解决问题的能力,开拓解题思维与视野.下面举例说明圆锥曲线定义在求解2020年有关高考题中的应用.
1 求参数的值
例1(全国卷Ⅰ理4)已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p=( ).
A.2 B.3 C.6 D.9
解析
利用抛物线的定义建立方程即可得到答案.设抛物线的焦点为F,点A到y轴的距离为9,即点A的横坐标为9,由抛物线的定义知|AF|=解得p=6,故选C.
点评
本题主要考查利用抛物线的定义计算参数p的值,考查学生转化与化归能力.
例2(全国卷Ⅲ理11)设双曲线(a>0,b>0)的左、右焦点分别为F1,F2,离心率为是C上一点,且F1P⊥F2P.若△PF1F2的面积为4,则a=( ).
A.1 B.2 C.4 D.8
解析
根据双曲线的定义、三角形面积公式、勾股定理,结合离心率公式,即可得出答案.因为,根据双曲线的定义可得|PF2|=4,即|PF1|·|PF2|=8.
因为F1P⊥F2P,所以|PF1|2+|PF2|2=(2c)2,所以(|PF1|-|PF2|)2+2|PF1|·|PF2|=4c2,即a2-5a2+4=0,解得a=1或a=-1(舍),故选A.
点评
本题主要考查了双曲线的性质以及定义的应用,涉及勾股定理及三角形面积公式的应用.
2 判断位置关系
例3(北京卷7)设抛物线的顶点为O,焦点为F,准线为l.P是抛物线上异于O的一点,过P作PQ⊥l于Q,则线段FQ的垂直平分线( ).
A.经过点OB.经过点P
C.平行于直线OPD.垂直于直线OP
解析
依据题意不妨作出焦点在x轴上的开口向右的抛物线,根据垂直平分线的定义和抛物线的定义可知,线段FQ的垂直平分线经过点P.如图1所示,因为线段FQ的垂直平分线上的点到F与Q的距离相等,且点P在抛物线上,根据定义可知,|PQ|=|PF|,所以线段FQ的垂直平分线经过点P,故选B.

图1
点评
本题根据线段的垂直平分线和抛物线的定义作出判断,考查了抛物线的定义的应用.
3 求长度
例4(江苏卷18,节选)如图2所示,在平面直角坐标系xOy中,已知椭圆的左、右焦点分别为F1,F2,点A在椭圆E上且在第一象限内,AF2⊥F1F2,直线AF1与椭圆E相交于另一点B.求△AF1F2的周长.
解析
根据椭圆定义可得|AF1|+|AF2|=4,从而可求出△AF1F2的周长.因为椭圆E的方程为F2(1,0).由 椭 圆 定 义,得|AF1|+|AF2|=4,所以△AF1F2的周长为4+2=6.
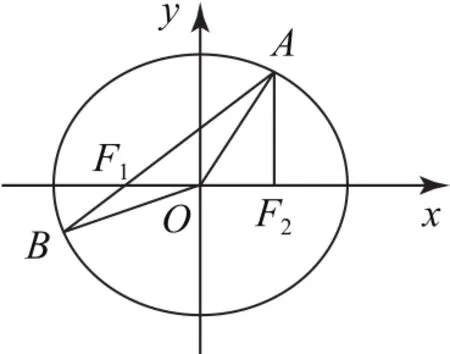
图2
点评
本题是椭圆定义的典型应用,一般地,已知椭的左、右焦点分别为F1,F2,点A是椭圆上的点,则△AF1F2的周长为2(a+c).
例5(新高考卷13)斜率为的直线过抛物线C:y2=4x的焦点,且与C交于A,B两点,则|AB|=________.
解析
先根据抛物线的方程求得抛物线的焦点坐标,再利用点斜式得出直线方程,与抛物线方程联立消去y并整理得到关于x的一元二次方程,最后利用抛物线定义求得结果.
因为抛物线的方程为y2=4x,所以抛物线焦点F的坐标为(1,0).又因为直线AB过焦点F且斜率为,所以直线AB的方程为y=(x-1),代入抛物线方程消去y并化简得3x2-10x+3=0,Δ=100-36=64>0.
设A(x1,y1),B(x2,y2),则.过A,B分别作准线x=-1的垂线,设垂足分别为C,D,如图3所示,则
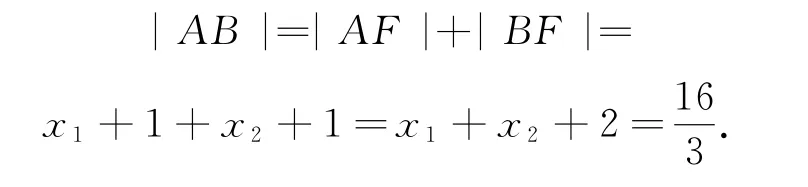
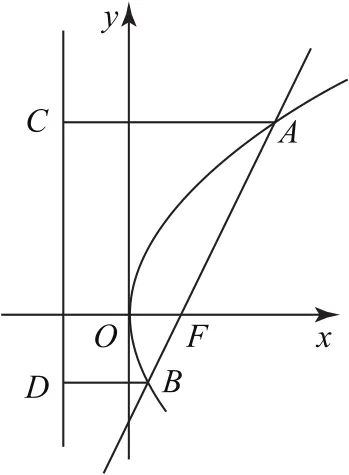
图3
点评
本题考查了直线与抛物线的位置关系,同时考查了抛物线定义的应用.
例6(浙江卷8)已知点O(0,0),A(-2,0),B(2,0).设点P满足|PA|-|PB|=2,且P为函数图象上的点,则|OP|=( ).

解析
根据题意和双曲线的定义,可知点P既在双曲线的一支上,又在函数的图象上,从而可求出点P的坐标,得到|OP|的值.
因为|PA|-|PB|=2<4,所以点P在以A,B为焦点,实轴长为2,焦距为4的双曲线的右支上,由c=2,a=1,可得b2=c2-a2=4-1=3,即双曲线的右支方程为而点P又在函数y=的图象上,所以由解得故选D.
点评
本题主要考查双曲线定义的应用,以及二次曲线的位置关系的应用,考查了考生数学抽象、直观想象和数学运算等数学核心素养.
4 求方程
例7(全国卷Ⅱ理19)已知椭圆(a>b>0)的右焦点F与抛物线C2的焦点重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点,且|CD|=.
(1)求C1的离心率;
(2)设M是C1与C2的公共点.若|MF|=5,求C1与C2的标准方程.
解析
(1)椭圆C1的离心率为(求解过程略).
(2)由(1)知a=2c,b= 3c,椭圆C1的方程为的方程为y2=4cx,联立C1与C2的方程,求出点M的坐标,再利用抛物线的定义结合|MF|=5可求得c的值,进而可得出C1与C2的标准方程.联立消去y并整理得3x2+16cx-12c2=0,解得或x=-6c(舍去).
因此,曲线C1的标准方程为曲线C2的标准方程为y2=12x.
点评
本题第(2)问考查了利用抛物线的定义求抛物线和椭圆的标准方程,考查计算能力.
圆锥曲线的定义是用圆锥曲线上的点到焦点的距离来刻画的,因此涉及圆锥曲线上的点到焦点的距离问题,灵活运用定义是问题获解的根本,它是相应标准方程和几何性质的“源”,对于圆锥曲线的有关问题,要有运用圆锥曲线定义解题的意识,“回归定义”是圆锥曲线问题重要的求解策略之一.

