减速带路面工况下线性和非线性模型悬架的最优阻尼比
戴振泳, 李 涛, 宋廷伦*, 提 艳
(1.奇瑞汽车股份有限公司, 芜湖 241006; 2.南京航空航天大学能源与动力学院, 南京 210016)
减速带对于降低汽车行驶速度,进而减少道路事故具有重要意义[1-3]。然而当汽车通过减速带时,会引起车身强烈振动,降低了乘坐舒适性和安全性。
汽车悬架作为减少路面传递至车身振动的重要组成部件,其阻尼比适当匹配直接影响车辆行驶的平顺性和操纵稳定性。目前,国内外学者对悬架阻尼比展开了大量研究[4-6], 探寻各个优化目标下的最优阻尼比。文献[7-10]通过理论仿真求解随机路面下的最优阻尼比,而针对减速带路面下悬架最优阻尼比的研究较少。
基于上述研究的理论基础,结合机械振动和汽车理论,建立正弦截面减速带路面模型和频率加权函数滤波网格,以1/4悬架线性模型和非线性模型作为研究对象,采用振动剂量值(vibration dose va-lue,VDV)和轮荷冲击系数k作为减速带路面下的平顺性评价标准,基于MATLAB/Simulink 仿真求解,探讨考虑车轮离地非线性,不同悬架限位块刚度非线性以及不同行驶车速下的悬架最优阻尼比。
1 正弦截面减速带模型的建立
减速带路面是车辆振动的输入。目前,常采用正弦截面、圆弧截面、梯形截面等作为路面减速带的常用断面形状。采用正弦截面形状减速带模型作为车辆振动的输入[11]。
正弦截面形状减速带由正弦曲线半个周期构成,如图1所示。
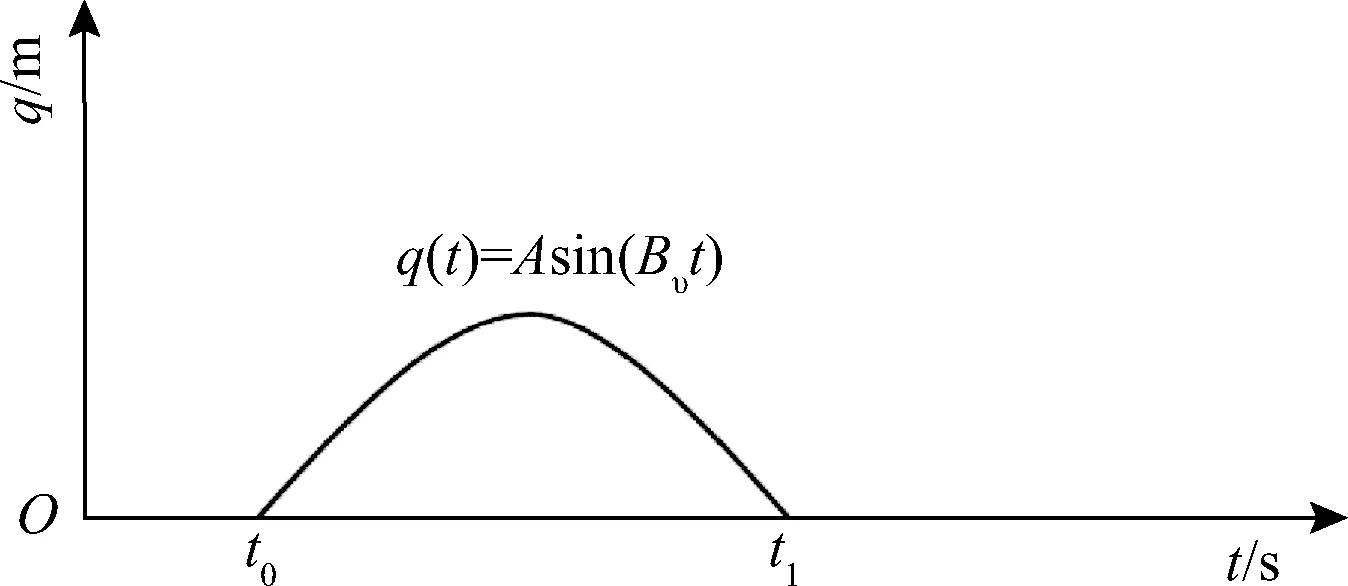
t0为行驶汽车初遇减速带时间;t1为行驶汽车离开减速带时间
假设减速带数学模型为
q(t)=Asin(Bυt)
(1)
式(1)中:q(t)为关于时间t的减速带函数;A为减速带截面高度;Bυ为关于车速的圆频率函数,其计算式为
(2)
式(2)中:L为减速带截面宽度,m;v为车速,m/s。
通过MATLAB/Simulink建模仿真,其中取v=5 m/s,A=0.05 m,L=0.4 m,t0=0.2 s。仿真结果如图2所示。

图2 减速带仿真
由图2可知,在车速为5 m/s的情况下,单个车轮通过减速带的时间为0.08 s, 与理论计算结果相吻合,验证了该模型的准确性。
2 减速带路面下的汽车平顺性评价标准
由于减速带路面输入使汽车系统输出的振动波形峰值系数大于9,根据ISO 2631-1:1997(E)所规定的基本评价方法——加权加速度均方根值,不适用于对大脉冲激励的评价,故采用辅助评价方法——加权加速度4次方和根值的方法来评价[12],它能够更好地估计偶遇大脉冲引起的高波形峰值系数振动对人体的影响。加权加速度4次方和根值的方法又称作振动剂量值VDV,计算公式为
(3)
式(3)中:T为暴露时间;aw为加权加速度均方根值。式(3)不仅考虑到汽车通过减速带时刻的振动响应,还考虑到汽车通过减速带后的振动表现。振动计量值越大,表征汽车平顺性越差。
当行驶车辆通过减速带时,不仅对驾驶平顺性产生影响,同时也对驾驶安全性产生不可忽视的作用。为了保证汽车驾驶安全性,需要最大程度降低车轮动载荷,从而尽可能避免由于车轮通过减速带而产生的车轮离地现象。此处引用轮荷冲击系数k作为评价汽车驾驶安全性的评价指标[3],计算公式为
(4)
式(4)中:Fz_max为车轮最大载荷;Fz_start为车轮静态载荷;Fzd_max为车轮最大动载荷。式(4)表征,当车轮动载荷越大,轮荷冲击系数越大,车轮跳离地面程度越大,汽车驾驶安全性越差。
3 二自由度悬架模型及频率加权滤波网格建立
目前乘用汽车均采用接近于1的轴荷分配系数进行整车设计,使得前后悬架振动相互独立解耦。由于二自由度车辆悬架模型结构简单,可以准确反映车辆基本平顺性动态特性[13]。故采用二自由度模型作为研究平顺性的基本模型。
线性二自由度模型,因为计算方便的特点,常用于车辆平顺性分析,然而所涉及的减速带路面输入,即脉冲激励输入,使得系统中车轮以及车身有较大位移变化。例如,当车轮经过减速带路面时发生的车轮离地和车轮撞击限位块等非线性场景,此处线性模型不能准确描述该状态。故同时建立线性二自由度模型和考虑车轮离地及车轮撞击限位块情况下的非线性二自由度模型,进行两模型对比研究。
3.1 二自由度悬架线性模型的建立
二自由度汽车悬架线性模型如图3所示。
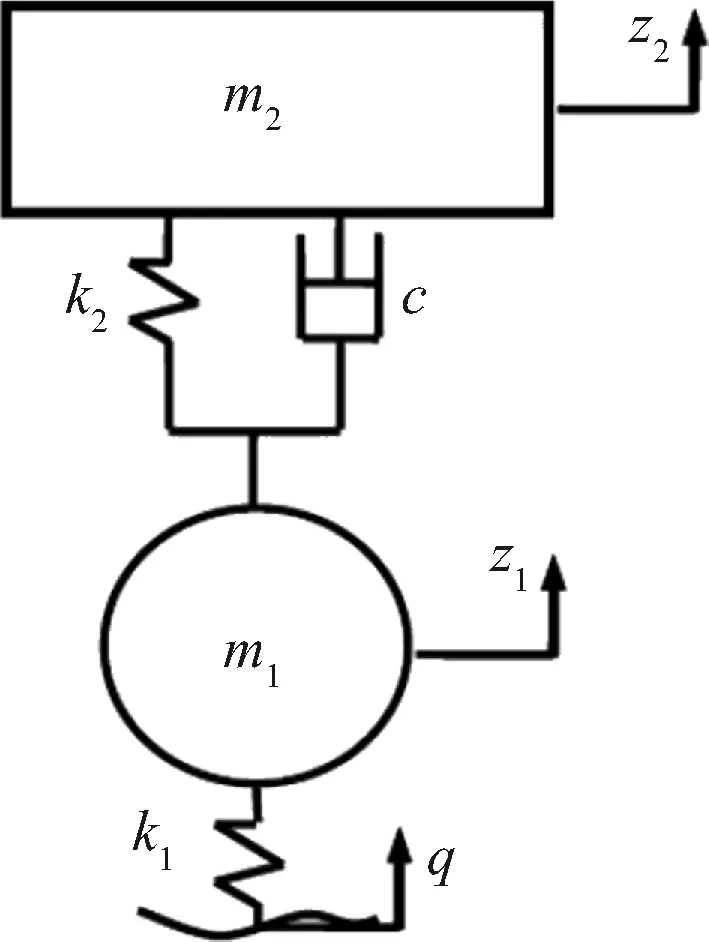
m2为簧载质量(车身质量); m1为簧下质量(车轮及车桥等质量); k2为悬架弹簧刚度;c为减震器的阻尼系数;k1为轮胎刚度;z1为车轮垂直位移;z2为车身垂直位移;q为路面不平度时域输入
取坐标原点为各自平衡位置,可建立其运动微分方程为
(5)
3.2 二自由度悬架非线性模型的建立
二自由度汽车悬架非线性模型如图4所示。求其运动微分方程为
(6)
式(6)中:减震器的阻尼力为
(7)
式(7)中:c为减震器的阻尼系数。

Fk2为悬架位移力; Fc为减震器的阻尼力;Fk1为接地力;其他参数定义同图3
由于限位块的刚度远大于悬架弹簧刚度,则考虑撞击限位块前后的悬架位移力Fk2,表达式为
(8)
式(8)中:k2为悬架弹簧刚度;k22为限位块刚度;H为悬架动挠度限位行程。
由于车轮离地后,轮胎与地面无接触,不会有相互作用力产生,此时,整个系统仅受到重力作用返回地面,由于线性系统建模时取各自平衡位置,进而忽略了重力和支撑力。此时考虑重力的非线性模型中,接地力Fk1表达式为
Fk1=k1(z1-q-Δs)+(m1+m2)g
(9)
式(9)进一步可写为
(10)
式中:Δs为系统处于静止平衡点时车轮垂向变形量。
3.3 频率加权滤波网格的建立
采用振动剂量值(VDV)作为汽车平顺性评价指标,其中aw(t)为时间历程下的加权加速度均方根值,通过相应频率加权滤波网格滤波后才能得到。依据ISO 2631-1标准[12],人体对于不同频率下的振动敏感程度不同,对于垂直轴向振动,人体敏感频率范围为4~12.5 Hz,其中4~8 Hz频率范围内,车身振动会与人体内脏器官产生共振,8~12.5 Hz频率范围内,车身振动会对人的脊椎系统产生严重不良影响。
对于垂向振动的频率加权函数w(f)表示为

(11)
式(11)中:f为频率,Hz。
汽车平顺性主要研究振动响应的幅频特性,而对相位差可忽略不予考虑,文献[14]采用带通滤波网格模拟标准频率加权函数,保证了4~12.5 Hz幅值的准确性,其他频率区间失真较为严重。参考式(11)设计相应的滤波网格,由于标准频率加权函数近似由多个理想惯性环节组成,故设计基于惯性环节的频率加权滤波网格,其传递函数为
(12)
通过式(12)可设计针对垂直方向振动的频率加权滤波网格,将其幅频特性与标准频率加权函数幅频特性进行对比,如图5所示。
从图5中可以看出,标准曲线与设计曲线尽管频段内存在一定误差,却极大地保留了曲线趋势,贴合度较高。在人体最为敏感的频段4~12.5 Hz,误差控制在0.05范围内,其他频率范围最大误差控制在0.2范围内,平均误差控制在0.1左右。因此,设计的频率加权滤波网格可以应用于时间历程下的加速度均方根值信号处理中。
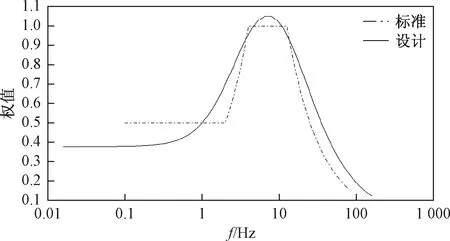
图5 频率加权函数对比
3.4 二自由度模型在减速带路面下的数值仿真验证
基于以上减速带模型及二自由度线性和非线性模型,通过Simulink建模,进行数值仿真验证。悬架模型仿真参数如下:m2=400 kg;m1=40 kg;k1=180 N/mm;k2=20 N/mm。非线性模型限位块刚度为10k2,限位块行程为0.05 m。汽车以5 m/s速度行驶0.2 s后通过减速带,比较线性和非线性二自由度车身加权加速度曲线变化,如图6所示。
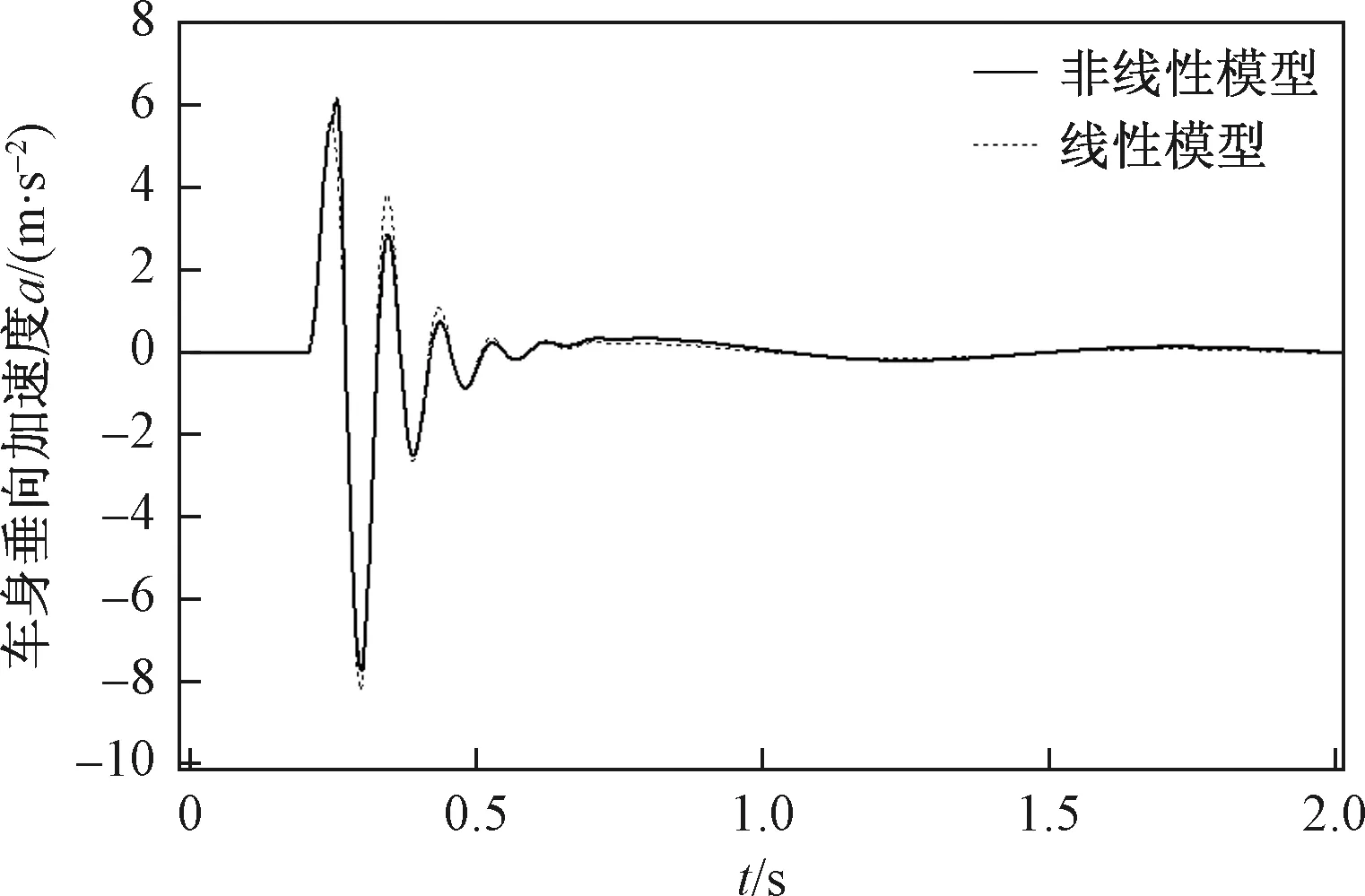
图6 二自由度模型验证
由图6可以看出,非线性模型和线性模型重合度较高,验证了二自由度非线性模型的准确性。同时比较曲线区别,非线性模型第一个正峰值高于线性模型,是由于该时间节点下,汽车通过减速带时的脉冲输入,导致悬架行程压缩过大,撞击限位块所致;而非线性曲线第一个负峰值绝对值小于线性曲线,是由于汽车通过减速带后,车轮跳离地面所致。而线性模型假设轮胎不会跳离地面,故该情况下,会用更大的弹簧力拉回车轮,有所失真。在车轮脉冲输入下,无论是悬架撞击限位块情况或车轮跳离地面情况都有可能发生,较大程度影响平顺性,不可忽视。
4 多因素下非线性及线性模型最优阻尼比对比
4.1 仅考虑车轮离地的非线性及线性最优阻尼比对比
行驶汽车通过减速带时,常会引起车轮离地现象,此处研究探讨仅考虑车轮离地的非线性模型与传统线性模型下对最优阻尼比的影响。
选择常用轿车通过减速带车速5 m/s (18 km/h)作为仿真车速,其他基础仿真参数如下:m2=400 kg;m1=40 kg;k1=180 N/mm;k2=20 N/mm。图7、图8分别为二自由度线性和非线性模型下振动剂量值VDV和轮荷冲击系数k随阻尼比ζ的变化曲线。
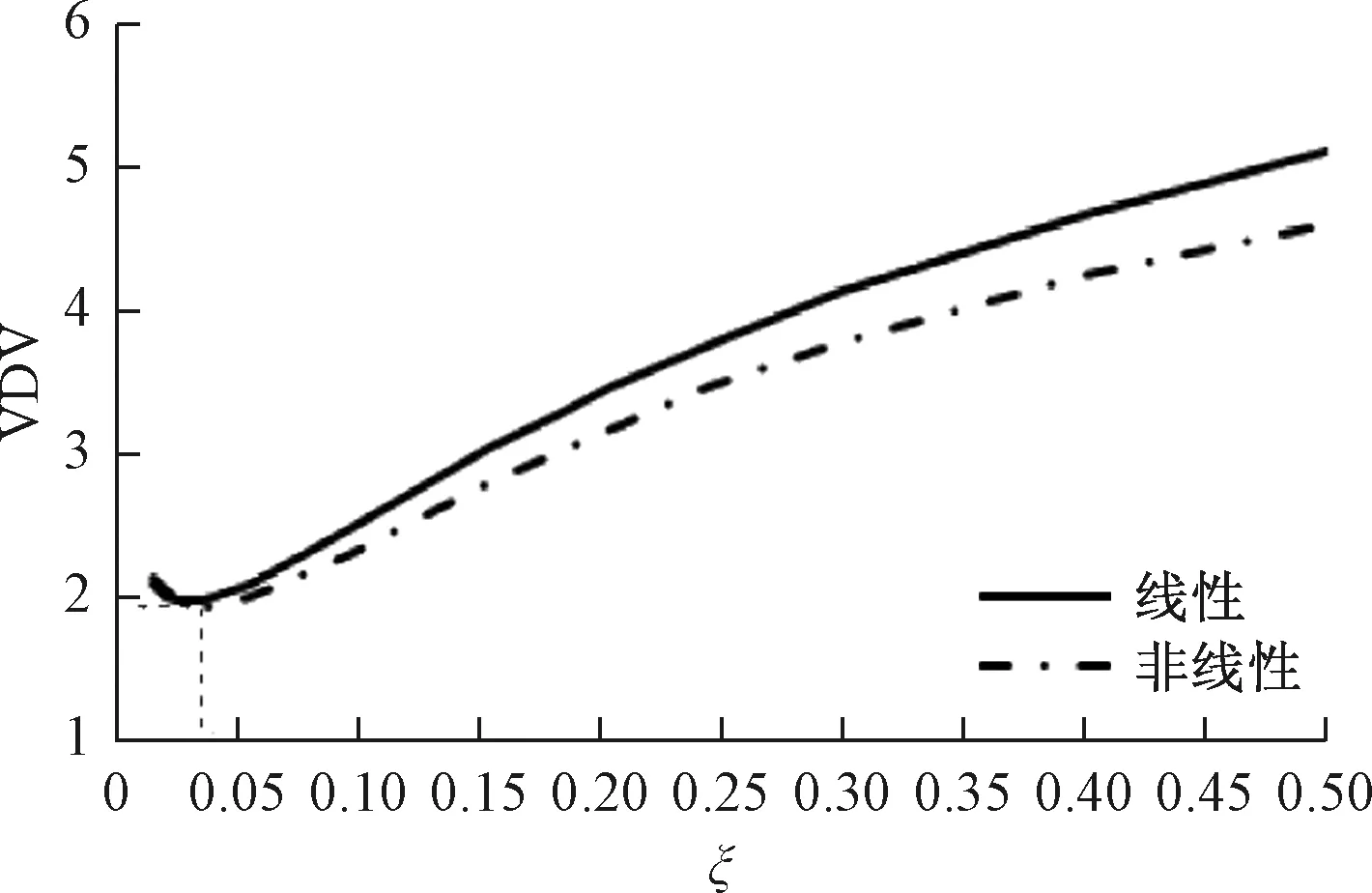
图7 仅考虑车轮离地非线性模型和线性模型VDV对比

图8 仅考虑车轮离地非线性模型和线性模型k对比
图8中,线性和非线性曲线均不重合,说明在该汽车使用参数和结构参数下,存在车轮离地现象。从图7可以看出,线性和非线性VDV仿真曲线趋势相同,均随着阻尼比的增加先减小后增大,且存在相同最优阻尼比ξs1,该最优阻尼比下两曲线的振动计量值较为接近,乘员乘坐体验最为舒适; 从图8可以看出,线性和非线性轮荷冲击系数k仿真曲线趋势也相同,存在公共最优阻尼比ξs2,然而,非线性仿真曲线由于考虑车轮离地情况,在车轮离开地面后,整车只受到重力作用返回地面,而线性模型当车轮离开地面后,车轮将受到大于整车重力的作用拉力返回地面,故非线性曲线整体轮荷冲击系数k较线性仿真曲线偏大,操纵稳定性偏差,更加接近真实情况。由于考虑车轮离地的非线性曲线趋势和线性曲线类似,但更加接近现实场景,故之后的数值仿真中,非线性模型均考虑车轮离地非线性情况。
4.2 考虑限位块刚度的非线性及线性最优阻尼比对比
车辆行驶通过减速带,有一定概率撞击限位块,为研究限位块刚度作为变量因素对最优阻尼比的影响,此处选取较小动挠度限位行程0.05 m。其他汽车基础结构参数、使用参数不变,比较线性模型和分别采用限位块刚度为5k2、10k2、15k2的非线性模型下(考虑车轮离地非线性)的最优阻尼比,k2为悬架刚度。仿真曲线如图9、图10所示。
图9、图10中,线性曲线和非线性曲线均不重合,说明在该汽车使用参数和结构参数下,存在撞击限位块现象。从图9可以看出,线性和非线性VDV仿真曲线趋势虽然相同,最优阻尼比却存在较大差异,线性模型仿真曲线的最优阻尼比为0.035左右,而非线性模型最优阻尼比平均为0.1以上,更加具有工程意义,进一步验证了非线性模型的准确性和可行性。在非线性模型曲线中,随着限位块刚度的增加,最优阻尼比不断增大,振动计量值VDV也不断升高,意味着增大限位块刚度不利于汽车平顺性。由图10可以看出,随着限位块刚度的增加,最优阻尼比不断增大,轮荷冲击系数却不断降低,意味着增大限位块刚度有利于操纵稳定性。以上仿真曲线可以看出平顺性和操纵稳定性的矛盾所在,例如要想提高汽车平顺性,需要减小限位块刚度,却导致操纵稳定性的恶化。这说明,实际工程中,在选择限位块刚度时,需要多方面衡量,全面考虑,在满足操纵稳定性的前提下,尽可能优化平顺性。
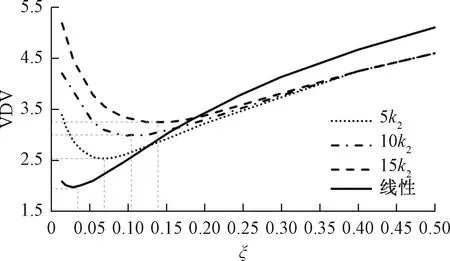
图9 考虑限位块刚度的非线性模型和线性模型VDV对比
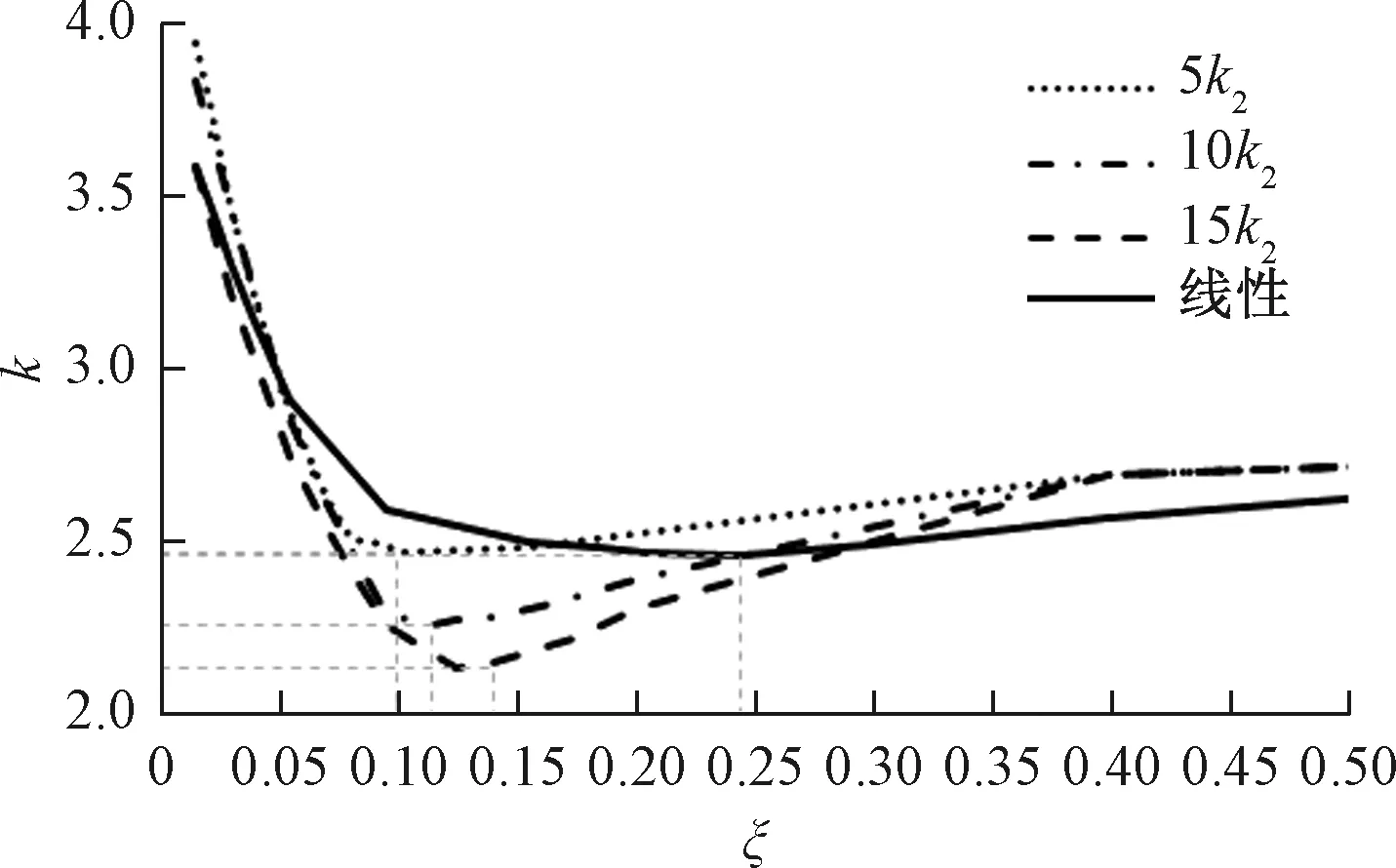
图10 考虑限位块刚度的非线性模型和线性模型k对比
4.3 不同车速下的非线性及线性最优阻尼比对比
本小结研究汽车行驶车速作为变量因素对最优阻尼比的影响。由于驾驶习惯及道路限速等限制条件,一般驾驶员通过减速带常用车速为15~40 km/h,使用线性仿真车速5 m/s, 非线性(考虑车轮离地和撞击限位块下)仿真车速5、7、10 m/s作为比较,分析相同车速下线性和非线性最优阻尼比的区别,以及不同车速非线性模型下最优阻尼比的变化。此外,选取限位块刚度为15k2, 其他汽车基础结构参数、使用参数不变。仿真曲线如图11、图12所示。
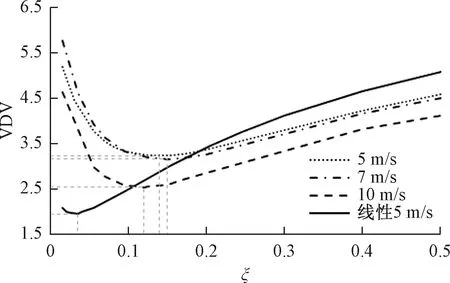
图11 不同车速下非线性模型和线性模型VDV对比
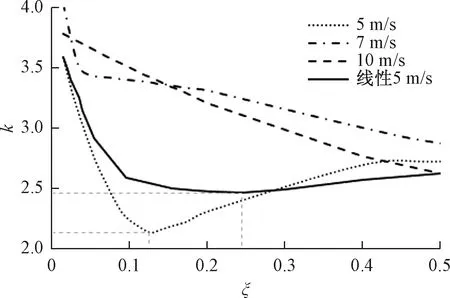
图12 不同车速下非线性和线性k对比
从图11可以看出,相同5 m/s行驶车速下,非线性仿真曲线最优阻尼比远大于线性曲线最优阻尼比,更加接近于实际工程值,振动计量值VDV也较高,平顺性相对表现较差。非线性模型下,不同车速,最优阻尼比不同,由于7 m/s车速下过减速带时,路面对车轮的激励频率更接近于系统固有频率,小阻尼时,其VDV大于车速为5、10 m/s时,汽车平顺性较差。汽车行驶时,应尽量避开该车速下通过减速带。其次,车速10 m/s的仿真曲线相比车速为5 m/s有较低的VDV,说明车速增大并不一定导致平顺性降低,然而本文未考虑车身部件结构强度,过高的车速通过减速带也会加剧车身零部件的冲击磨损;从图12可以看出,当前仿真车速中,当且仅有5 m/s车速下存在最优阻尼比,且非线性最优阻尼比大于线性最优阻尼比,轮荷冲击系数k相对较大,操纵稳定性相对表现较差。
5 结论
建立正弦截面减速带及二自由度悬架线性、非线性模型,同时基于振动剂量值VDV的时域法设计频率加权滤波网格,研究探讨考虑车轮离地非线性,不同悬架限位块刚度非线性以及不同行驶车速下的悬架最优阻尼比。
研究表明,仅考虑车轮离地非线性不会影响最优阻尼比,当考虑撞击限位块时,不同限位块刚度及不同车速都决定不同最优阻尼比。阻尼半主动控制策略中可通过汽车传感器实时测量出路面减速带断面高度、宽度和自身车速,进而实时调整悬架系统阻尼系数,维持最优阻尼比通过减速带,从而提高乘员舒适性和操纵稳定性。

