单向冻结条件下兰州地区黄土的温度场变化规律

张 正, 马学宁, 王 聪

(兰州交通大学土木工程学院, 兰州 730070)

冻土是指温度低于0 ℃且含冰的岩土,其由水、冰、气体和固体矿物颗粒组成[1]。冻土是一种不同于普通土的的特殊土体,是一种多相体系,性质受未冻水含量和含冰量的控制,而含冰量与温度的变化密切相关。中国冻土分布面积广大,永久性与季节性冻土面积约占中国陆地总面积的2/3,冻土主要分布在中国西北和纬度较高的东北地区[2]。随着“一带一路”的进一步推进,冻土地区将进行大量的重大工程建设。这些工程在低温作用下不可避免的会产生冻胀和融沉病害问题,比如水平冻胀力造成支挡结构和输水渠道的破坏,冻胀造成公路路面开裂、造成铁路轨面不平顺,这些问题都是冻土地区工程建设所要面对的挑战,因此对冻土温度场及其变化规律进行深入研究显得尤为重要。确定未冻水与热参数之间的联系,进而准确计算冻土温度场对于提升寒区工程建设质量、冻害处理和人工冻结法施工中的温度场预测精度具有重要作用。

随着冻土温度场计算理论的发展,中外学者对冻土热参数测试和冻结温度场计算进行了相应的研究。Vinson等[3]、Ling等[4]研究了含水率对冻结土体动态特性的影响。李岩等[5]应用三维模拟冻结实验系统,对竖向直排冻结条件下不同深度土体的水平冻胀力分布进行了模型试验研究。胡坤等[6]通过一维冻胀实验研究了多种不同约束条件下土体水分场、冻胀量、冻胀率和冻胀力的变化规律以及土体冻胀量与冻胀力之间的关系。在冻土温度场计算方面,胡向东等[7]推导了环形单圈冻结管稳态温度场的解析解,通过数值计算方法进行了验证,并提出了简化的解析公式。张明礼等[8]以单向冻结下的垂直土柱实验结果为基础,应用COMSOL Multiphysics软件的数学模块实现了考虑冰水相变和水分对流的温度场与水分场的偏微分耦合方程的求解,分析了冻土水分对流和温度变化的关系。沈世鑫[9]通过数值模拟方法研究了多年冻土区公路路基温度场分布规律,对冻土地区路基温度场的影响因素及其分布进行了分析研究。夏锦红等[10]基于MATLAB PDE工具箱对冻土温度场的一维热传导进行了计算。胡俊等[11]运用有限元软件ADINA建立了三维数值模型,分析研究了大直径杯型冻土壁温度场的发展变化与分布规律。蔡海兵等[12]运用有限元软件ABAQUS对某地铁联络通道的冻结温度场进行了数值计算。王彦洋[13]运用FLAC3D对地铁联络通道的冻结法施工进行了数值模拟,分析了冻结过程的温度场的变化规律。王心同[14]结合东北地区某新建客运专线工程,通过经验计算、理论分析和数值模拟,对比分析了中俄两国冻结深度的计算方法,并通过建立了非稳态路基温度场有限元计算模型分析研究了深季冻区路基温度场分布规律。

中外学者对土体冻胀机理、冻胀特性、冻胀力的发展规律、冻害治理措施和冻害预测模型做了大量的研究,发现了大量规律并提出了许多理论。但采用室内模型试验对单向冻结下土体温度场变化规律的研究较少。现以兰州黄土为研究对象,室内模型试验和数值模拟相结合,研究在单向冻结过程中土体温度的变化规律,给出土体温度的变化曲线。以期通过不同含水条件下黄土单向冻胀实验来探索黄土冻胀灾害防治的有效措施和方法。

1 模型实验

1.1 材料性质

实验土料取自甘肃省兰州市九州台地区,基本物理指标依据《铁路工程土工试验规程》(TB 10102—2010)[15]中的相关规定进行。试验测得黄土基本物理指标如表1所示。

表1 黄土基本物理指标

1.2 实验装置

实验采用单向封闭冻结实验系统,实验系统可以按照实验要求控制温度,该系统由温度控制系统、环境箱和模型箱、测量系统3部分组成,如图1所示。

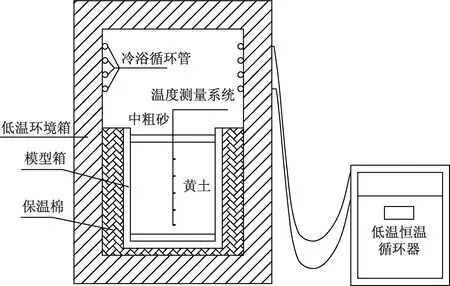
图1 实验系统示意图

温度控制系统使用杭州雪中炭恒温技术有限公司生产的低温恒温循环器,其输出温度范围为-30～+50 ℃,精度0.2 ℃,循环液使用无水乙醇。模型箱由角钢和有机玻璃制成,尺寸为80 cm×60 cm×80 cm,侧壁和底部粘贴10 cm厚的保温棉,并且在模型箱和环境箱之间的空隙中填充保温棉从而实现试验设计的单向冻胀,保温棉的导热系数为0.03～0.035 W/(m·K),保温棉的导热系数约为土体导热系数的2%～3.5%,故可以认为试验设备温度边界条件能满足单向冻结条件。

测量系统包括：①土体温度的测量。温度测量采用铂热电阻pt100,其工作范围为-50～+200 ℃,精度为0.1 ℃；温度测量传感器从土体上表面开始沿深度方向每隔12 cm布设一个。②数据采集。使用LCXAF温度巡检仪和安装相关采集软件的计算机,实验仪器实物如图2(a)所示。

1.3 实验方案

研究采用封闭单向冻胀模型实验,来模拟冷源单向冻结条件。两组实验中土体的含水率分别为14%、16%,压实度为0.9,按照实验方案将拌和均匀的土分层填入模型箱,填土过程中将温度传感器按照试验要求埋设在相应位置,填筑完成后将箱内土体静置48 h,使土体中水分分布均匀。冻结阶段环境箱温度设定为-20 ℃,实验开始后开启低温恒温循环器使环境温度快速达到实验设定值然后保持温度恒定,当土体温度下降到实验方案的设计值时,冻结阶段结束；将环境箱温度调至20 ℃并保持恒定来模拟融化过程。实验模型填筑完成后如图2(b)所示。

图2 模型实验装置实物图

2 实验结果分析

2.1 温度场分析

各阶段土体温度沿土体深度变化分别取不同时刻的数据,以土体温度为横坐标,温度传感器距离土体顶部的深度作为纵坐标,得到土体在不同冻结时刻土体温度T变化规律如图3所示。实验结果表明,不同含水率w土体温度变化规律一致,沿深度h呈线性变化。冻结阶段初期温度下降较快,后期逐渐减慢,温度下降速度在-0.4 ℃附近最慢。

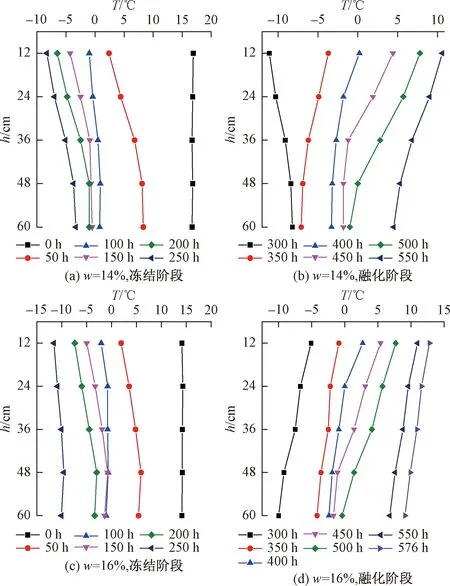
图3 实验土体温度沿深度的分布规律

图4所示为一个冻融循环周期试验过程中土体不同深度处温度的变化曲线。以土体含水率14%、16%的结果为例进行说明,环境箱内的温度在实验开始20 h后达到实验设计的温度并且保持稳定。实验进行312 h后有冻结状态转变为融化阶段,环境温度快速上升到实验设定的温度20 ℃。由温度变化曲线可以看出,距冷端表面较远处的土体温度曲线呈现出对称变化,降温速率相近。接近土体表面的点,土体冻结和融化过程曲线差异较大,升温的速率大于降温的速率并且在-0.4 ℃出现转折,降温阶段的温度变化速率为0.051 ℃/h,升温阶段的温度变化速率为0.156 ℃/h。

当温度变化至-0.4 ℃时距离表面较远处的土体温度变化曲线出现一个平稳阶段,温度变化曲线基本平行于横坐标,并且在降温和升温两个阶段表现出很强的对称性。出现这一现象的主要原因是土体中的水分在相变过程中释放潜热,并且含水率越高现象越明显。冻结后期(土体温度从-0.4 ℃下降到试验降温结束)各深度土体的温度下降速率较慢,这主要是土体冻结后土体导热系数和比热容发生了变化。含水率不同的土体温度变化规律相似,土体不同深度处的升温过程与降温阶段对称。

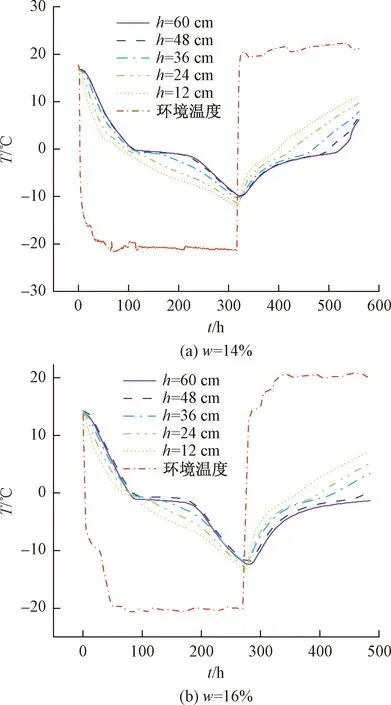
图4 试验温度变化曲线

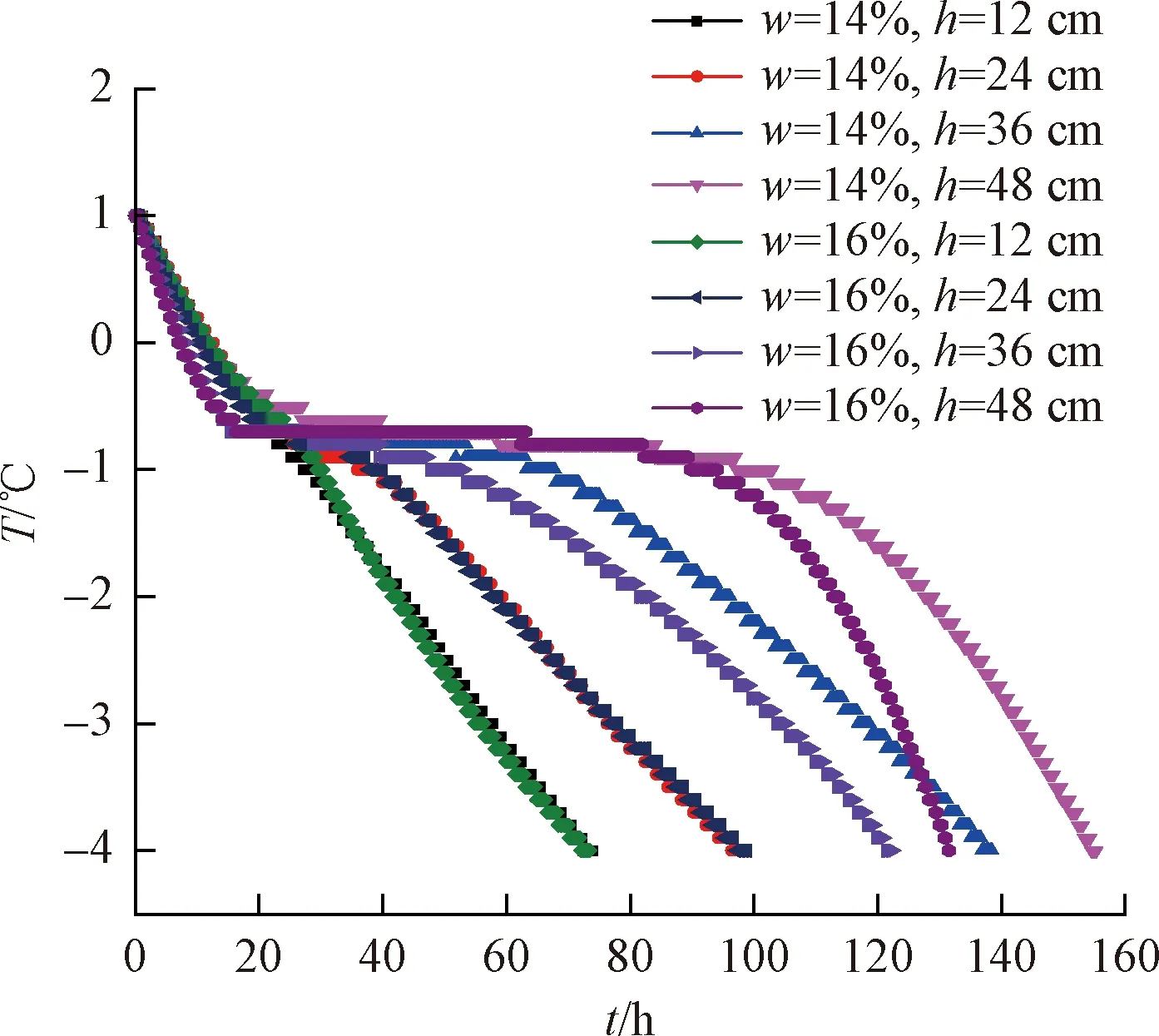
图5 不同含水率下土体的温度变化曲线

2.2 含水率对温度的影响

影响土体冻胀特性的因素有土质、含水率、温度和压实度等。而在相同的土质条件下,含水率则是冻胀的主要影响因素。分别进行了不同含水率的试验,选取-4～1 ℃区间的土体各个位置温度数据绘制图5。结果表明,不同含水率条件下的土体的温度的变化规律相似,含水率越高土体的降温速率就越快,土体冻结后更明显,含水率对平稳阶段影响有限。越靠近土体上表面土体的温度变化趋势越接近,在深度12、14 cm处的温度曲线基本重合。

3 数值计算

3.1 数值计算实现

数值计算采用COMSOL Multiphysics 软件中的孔介质模块和理查兹方程模块进行数值模拟。考虑相变的热传导微分方程为

(1)

式(1)中：C为土体的体积比热容，J/(m3·K)；λ为土体的导热系数，W/(m·K)；T为温度，℃；t为时间，s；为微分算子,对于二维问题为[∂/∂x,∂/∂z],x和z为直角坐标，m；L为水的相变潜热，J/kg,取值为3.35×105J/kg；ρi为冰的密度，kg/m3；θi为冻土中冰的体积含量，%。

土体中未冻水的迁移遵循达西定律,根据有相变项的Richard方程,非饱和冻土中未冻水迁移的微分方程为

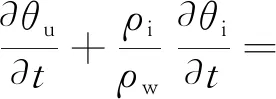
(2)

式(2)中：D(θu)为非饱和冻土的水分扩散系数，其主要由于含水量的差异引起，m2/s；Kg(θu)为非饱和冻土重力方向的导水系数,表示单位水力梯度下的流量，m/s；θu为冻土中未冻水的体积含量，%。

土体中的水分在降温冻结成冰的过程中存在着相的变化,为了克服某些变量在相变区间内存在数值突变,造成计算过程中难以收敛等问题,计算过程中认为冰水相变只发生在冻结温度附近一个很小温度范围内,在此区间内相变过程逐渐完成,因此引入阶跃函数来表征冻结过程中冰水相变过程,设置过度区间为0.4 ℃。相变过程设置如图6所示。

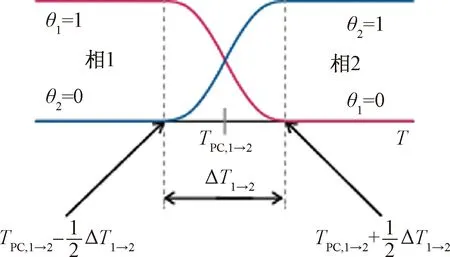
TPC,1→2为相1与相2之间的相变温度；ΔT1→2为相1与相2之间的转变间隔；θ1为相1的体积含量；θ2为相2的体积含量

土体的初始温度为16 ℃,环境箱温度同试验设定值,上表面为第三类边界条件,其余为绝热边界条件；土体初始含水率分别为14%、16%、18%,边界条件为无流动；网格划分采用预定义的超细化的映射网格；设置求解时长为578 h,求解步长为0.1 h,计算土体内部的温度场。

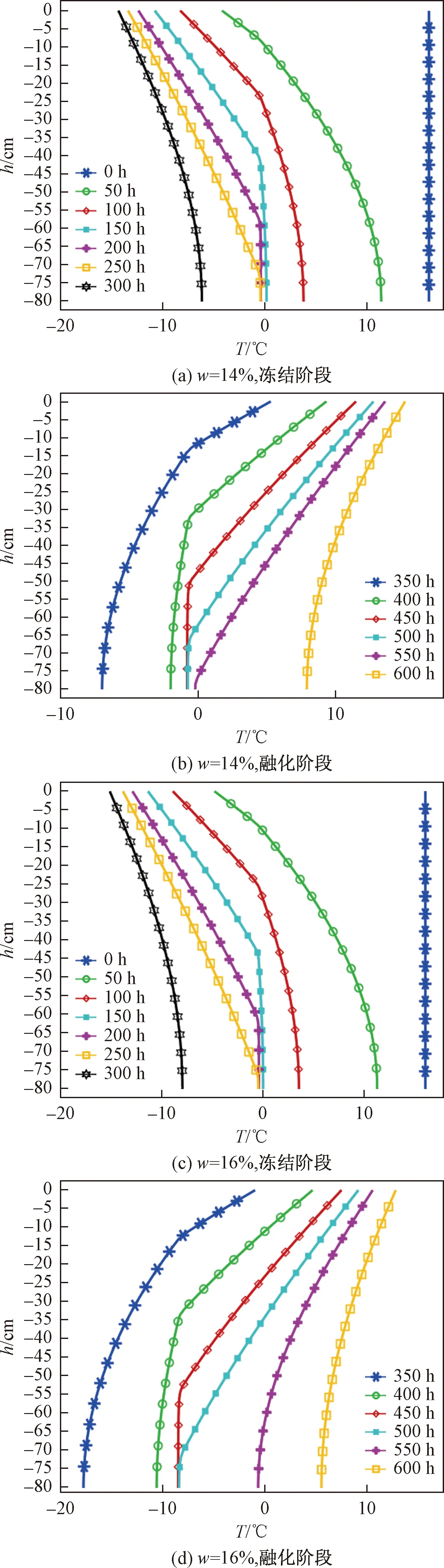
图7 不同条件下温度沿深度的分布规律

3.2 数值计算结果分析

不同含水率下土体温度的变化趋势相似,以含水率14%、16%为例进行说明。不同条件下土体温度沿深度变化规律如图7所示,数值计算结果与模型试验规律基本一致,土体温度沿深度线性变化,由于水冻结变为冰之后导热系数和比热发生会变化,所以曲线在-0.4 ℃出现转折点。在冻结阶段土体冻结前100 h温度下降较快,然后逐渐减慢-0.4 ℃左右下降最慢。融化阶段土体变化规律与冻结阶段类似。土体温度数值计算结果与实验值变化规律基本一致,冻结阶段数值计算结果稍低于实验值,融化阶段则相反。

对比图4、图8可知,数值模拟的土体各点温度变化曲线与模型实验实测的温度变化曲线发展规律基本一致,建立的数值计算模型能较为准确地计算冻土温度场变化规律。冻结初期土体与空气之间的温度梯度较大,热量交换剧烈,土体温度迅速下降。随着冻结时间的增加,土体与空气之间的温度梯度减小,土体温度下降缓慢。温度下降至-0.4 ℃左右出现平缓段,最后温度快速下降。对比不同深度处测温点结果可以看出,-0.4 ℃以下时,数值模拟的降温速率稍大于试验实测降温速率。可能存在以下几方面原因：①模拟中相变潜热的设置与实际试验情况存在差别，随着土体冻结时间的增加,土体中的水分达到冻结温度后开始结冰并释放大量潜热,会导致土体降温速率变慢；②试验所测的导热系数和比热容不够准确,数值计算中设置导热系数和比热容为线性变化与实际存在误差；③模型箱四周填充保温材料,不是理想的绝热条件。

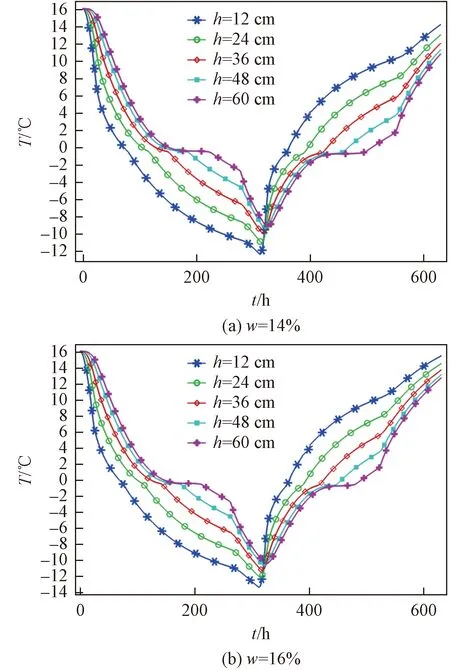
图8 土体温度场变化曲线

由图9可知,不同含水率下,靠近冷端位置土体含水率对温度的影响相对较小,变化曲线基本重合,这主要是含水率的变化幅度较小并且热量交换剧烈。不同含水率在试验初期温度差值较小,随着土体的冻结,温度在-0.4 ℃附近差值逐渐增大,土体含水率越高土体温度下降越快。

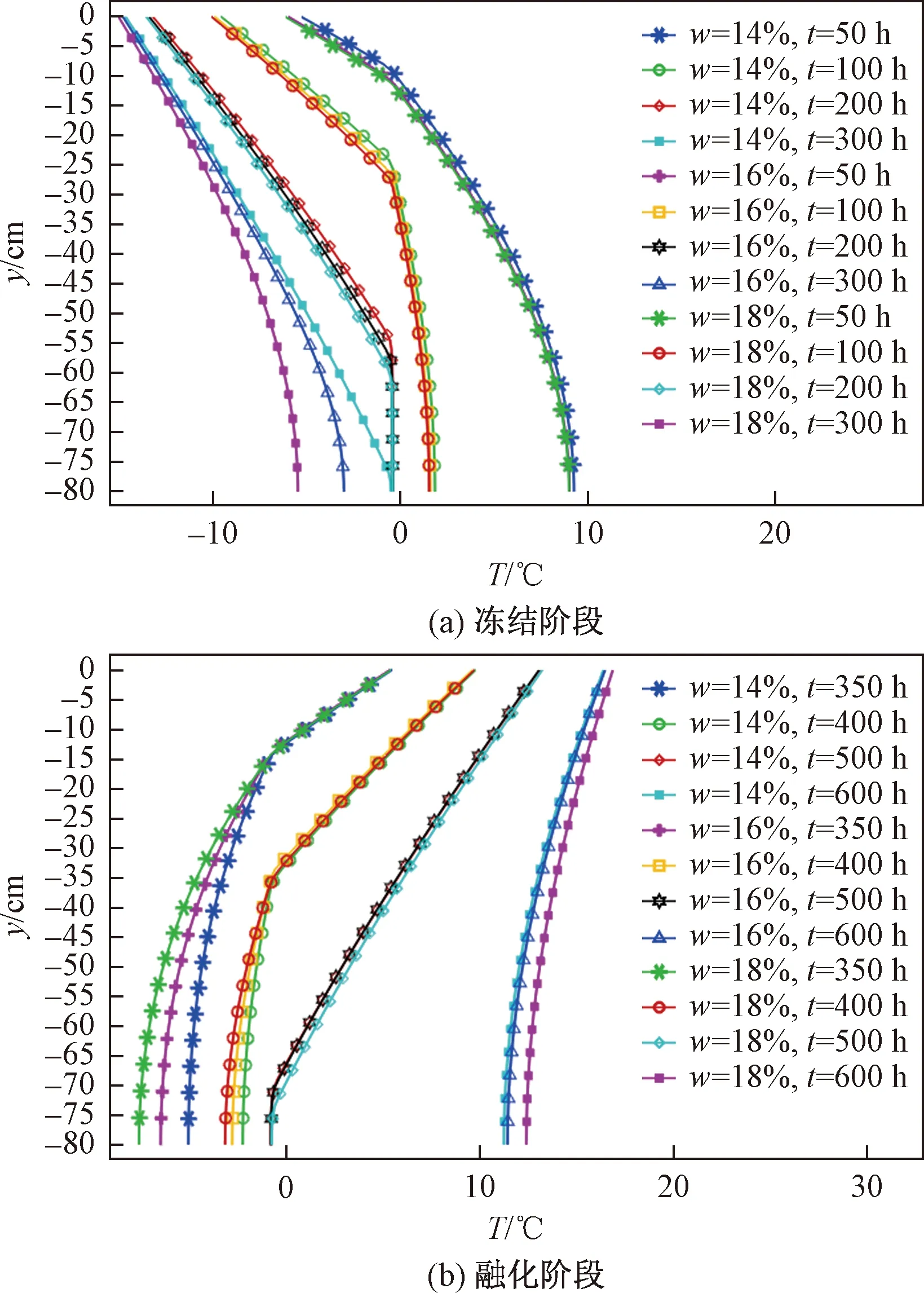
图9 不同条件下温度沿深度的分布规律

4 结论

通过室内封闭单向冻胀模型试验研究了兰州地区黄土的温度场的变化规律,得到如下主要结论。

(1)土体不同深度处的降温过程可分为3个阶段,第1阶段在冻结初期各深度土体的温度下降速率较快；之后土层各深度在-0.4℃附近降温速率曲线近乎平行于横坐标的平稳段；第3阶段在-0.4 ℃末端土体温度继续降低,下降速率较第1阶段有所减缓,且含水率越高这种现象越明显；冻结后期各深度土体的温度下降速率较慢。

(2)含水率不同的土体其温度变化规律相似,土体不同深度处的升温过程与降温阶段对称。

(3)含水率越高土体降温速率越快,土体的最终温度也越低。平稳段的长度与含水率的关系不明显。

(4)土体温度数值计算结果和模型实验值规律基本一致,建立的数值计算模型能较为准确地计算冻土温度场的变化与分布规律。