循环荷载下结构性黏土的动力特性试验研究

臧 濛， 太 俊， 汪为巍

(1.武汉轻工大学土木工程与建筑学院, 武汉 430023； 2.中国市政工程中南设计研究总院有限公司, 武汉 430010)

天然沉积黏土大多具有结构性,世界各国各地均有结构性土的存在,中国沿海地区广泛也分布着深厚的软黏土层,这些软黏土的含水率大、透水性差、孔隙比大、具有一定的流变性和触变性,而沿海地区的机场、高速公路、地铁等大型交通工程都建在软黏土地基上,投入运营之后必然会受到循环荷载作用,对工程造成了较大的安全隐患。如温州机场跑道由于飞机起降造成地基沉降,建成4年后工后沉降达16.6 cm,远高于机场跑道的容许沉降值,严重影响了机场跑道正常使用,增加了维修成本[1]。日本Saga机场道路开放通车后,3年运营期内交通荷载产生的附加沉降达到15 cm左右[2]。

软黏土地基在动荷载下失稳或工后沉降过大,通常与软黏土的结构性及动力学特性有关,当软黏土所受动荷载在其结构强度能承受的范围内,土体结构不会发生明显变化,土体变形也较小；而一旦动荷载作用导致结构强度丧失,土体会产生较大变形。对于结构性黏土,尤其是强结构性土,结构破坏前土体的轴向应变均较小且没有明显先兆,呈突然破坏特征, Seed等[3]、陈颖平等[4]、臧濛等[5]在对黏土进行的不排水循环荷载试验中都观察到这种现象。结构性黏土在长期循环荷载作用下可能会经历结构强度的丧失,这将会导致地基土产生大变形而失稳,引发土体的灾难性破坏,故需要特别考虑结构性对土体动力响应特征的影响。

软黏土由于结构性表现出与重塑土不同的工程性状,目前针对结构性土的动力响应研究较多,黄珏皓等[6]对循环轴向偏应力和循环围压耦合作用下宁波饱和重塑软黏土的孔压试验研究表明,孔压随循环应力比、循环围压的增加而增大,随振动频率的增加而减小。何绍衡等[7]通过不排水连续-停振循环三轴试验,发现荷载间歇对原状淤泥质软土的长期动力特性有显著影响。王家全等[8]探究了相同动应力比和相同动应力幅值下围压对加筋砾性土应变、模量和动孔压的影响,表明了加筋砾性土具有良好的抗液化性能。综上所述,以往开展的土体循环荷载作用下的动力变形特性研究一般以砂砾土、重塑土或中等、弱结构性黏土为主。然而,重塑土和原状土之间在结构上存在着很大的差别,即使人工制备结构性土也难以反映天然结构性黏土的工程特性[9-10]。原状结构性黏土能够反映地质历史时期的沉积过程和天然环境与土体的相互作用,臧濛等[5]研究表明结构性黏土的临界动应力和动强度与结构损伤密切相关,而固结压力增长造成的土体结构破坏程度对天然黏土动力特性的影响,以及当结构性黏土的结构破坏后,原状黏土尤其是强结构性黏土的动力变形特性是否逐渐趋于重塑土则鲜有比较研究。

因此,为了保证越来越多大型建、构筑物的安全与稳定,减少工程事故的发生,研究循环荷载作用下土结构性改变对结构性黏土动力特性影响具有重要意义。现开展一系列不同固结压力下湛江原状土与重塑土的不排水循环加载三轴试验,对结构性黏土在动荷载下的变形、强度及孔压特性进行系统性的试验研究。

1 试验土样及方案

试验仪器为英国GDS公司的饱和-非饱和动三轴试验系统DYNTTS,动三轴试验系统由GDSLAB软件来控制,通过不同的加载路径,可开展一系列循环加载三轴试验。土样取自广东省湛江市,物理力学性质指标如表1所示,该黏土具有含水率高、孔隙比大、液塑限高和竖直方向上渗透系数低的物理特性,同时,由无侧限抗压强度试验及十字板剪切试验可知,湛江原状黏土具有较高的力学强度指标。天然状态下,湛江黏土的压缩变形性状具有结构性土分段式的压缩曲线特征,存在明显屈服点,是一种典型的结构性黏土。

表1 湛江黏土基本物理力学性质指标平均值

土的动力特性试验的影响因素很多,包括固结应力水平、动应力幅值、静偏应力、振动频率、振动次数、土体饱和度等,此外,土的结构性、应力历史等也会影响土的动力特性。主要考虑结构性对土体动力响应的影响,为了体现固结应力水平造成的土体结构损伤对天然黏土动力特性的影响,试验方案中最大围压应大于土的结构屈服强度,故选取100、200、400 kPa 3种围压,与之对应有相同固结压力的重塑土动三轴试验,实现与原状土对照。试验方案如表2所示,围压为σ3,循环动应力比ηd=σd/σ3,其中σd为循环动应力,振动频率f=1 Hz。原状样由固定活塞的薄壁取土器钻取,室内推土器缓缓推出后经切土器切成圆柱形试样,尺寸为φ38 mm×76 mm,重塑土采用揉搓法备样,试样先等压固结,再进行不排水循环三轴试验,试验终止条件为轴向应变ε达10%。

表2 湛江土在不同动应力下的循环三轴试验

2 试验结果与分析

2.1 湛江原状土和重塑土的动变形特征

循环荷载作用下土体会产生累积塑性变形,动应力幅值的大小对累积塑性应变的增长规律有重要影响,由图1、图2中原状土和重塑土在不同围压不同动应力幅值下的应变与振次曲线可知,饱和软黏土的应变发展形态主要有“稳定型”和“破坏型”。当动应力幅值小于临界动应力时,试样应变曲线为“稳定型”,振动过程初始阶段,试样的应变有所增加,但随着振动次数的增大,应变增长速率逐渐衰减,应变趋于稳定,整个过程土样应变一直较小。而当动应力幅值大于临界动应力,应变曲线则为“破坏型”,与稳定型曲线的差别在于,当循环荷载作用到一定次数后,应变出现转折,土样变形开始急剧增大,随后在很少的循环振次范围内就产生大变形而破坏。

图1 原状土在不同围压下的应变与振次曲线

图2 重塑土在不同围压下的应变与振次曲线

对比围压σ3=100 kPa下原状土和重塑土的应变与振次曲线[图1(a)、图2(a)]，其应变曲线形态具有明显差异性,原状结构性黏土在循环荷载作用下的破坏突然,具有脆性破坏特征,原状土的应变-振次曲线达到一定的应变后呈快速增长型,应变曲线存在明显的转折,而重塑土的应变发展则呈现逐渐增长至破坏。为了观察湛江原状土应变-振次曲线的拐点,试验结果仅示意了轴向应变ε≤6%的应变-振次曲线。某一动应力下,土的变形介于 “稳定”与“破坏”的中间状态-“临界”状态,此时对应的动应力定义为临界动应力,σ3=100 kPa时原状土的临界循环应力比明显大于重塑土的临界循环应力比,随着循环动应力比ηd的增加,原状和重塑土样发生破坏所需的循环振次均不断减少。随着固结应力水平的增大,原状土的临界循环应力显著降低,而重塑土的临界循环应力变化则相对较缓慢,不同固结压力下重塑土的应变曲线形态以及临界循环应力基本一致。

然而当σ3=400 kPa时,如图1(c)所示,原状土脆性破坏特征逐渐变得不那么明显,随围压增大,原状土在不同动应力幅值下的轴向应变-振次关系曲线逐渐向重塑土的逐步增长型应变曲线发展,且原状土的临界循环应力比仍在显著下降,当固结压力超过结构屈服应力时,即使动应力比ηd小,软黏土的变形发展也很快。

从土体微观结构分析,原状黏土在结构破坏前为大孔隙空间结构,是构成土结构的基本形态,亚稳定的凝絮结构和颗粒间的强胶结作用[11],使土体结构在外力作用下不易破损。当随着固结压力的增大,原状土的结构逐渐破坏,土性逐渐趋于重塑土。重塑样制备方法是揉搓法将较大的结构单元破碎,土体内部大多为排列无序的较小土颗粒单元,颗粒间联结力较低,容易发生错动和移动,在较小的动应力下土体也会迅速发生塑性变形直至破坏。

2.2 破坏标准和动强度

土在循环荷载作用下的动强度一般理解为一定动荷载振动次数下满足某一破坏标准所需的动应力[12]。对于循环荷载作用下的结构性饱和软黏土,一般采用动荷载作用过程中变形达到某一破坏应变作为破坏标准,以便在土体破坏之前就能采取相应的防治措施。

不同的学者根据不同的研究对象和工程控制标准提出了不同的破坏应变标准。Seed等[3]对压实黏土在交通荷载作用下土体的变形特性研究中,提出将轴向应变达到5%作为应变破坏标准,Lee[13]利用两种灵敏性原状黏土进行循环三轴试验,发现灵敏性黏土在动荷载下会形成剪切破坏面,之后土体将发生非常大的变形,并提出以3%单幅应变作为判定灵敏性黏土破坏的一个应变标准,陈颖平等[4]将动荷载作用过程中变形开始急速陡转时的转折点作为破坏标准,将破坏应变与破坏振次之间进行曲线拟合。图3绘出σ3=400 kPa的重塑土在不同破坏应变标准(2%、3%、5%)下的动强度曲线,可见在同一围压相同振次条件下,随着破坏应变标准的增大,动强度增加。

图3 重塑土在不同破坏应变标准的动强度曲线(σ3=400 kPa)

根据湛江重塑土的变形特征,采取Seed等[3]提出将轴向应变达到5%作为应变破坏标准,而对具有突然脆性破坏特征的天然结构性黏土,将应变急剧增加时的转折点作为破坏标准,如图4所示为不同固结压力下原状土的转折应变。采取ε-lgN曲线,不同固结压力下原状土的转折应变均在3%左右,与Lee[13]提出的以3%的应变作为判定灵敏性黏土破坏标准基本一致,但随着围压的增加,转折应变略有增长,说明随着围压的增加,土体的脆性破坏特征会逐渐趋于不显著。对于结构性黏土来说,为防止土体结构的坍塌性破坏,需谨慎选择合理的特征点作为应变破坏标准,重塑土则一般可以结合实际工况对变形的要求来确定合适的强度破坏标准。

图4 不同固结压力下原状土的转折应变

在应变破坏标准下得到土的动强度规律,均可以表示为达到上述破坏标准时的振次N与动应力幅值σd之间的关系,表示为循环动应力比与循环次数即σd/σ3-N曲线,称为土的动强度曲线。采用转折应变作为破坏标准的原状土的动强度曲线如图5(a)所示,与图5(b)中重塑土在不同围压下的动强度曲线差异性十分明显,随围压的增大,原状土的动强度曲线迅速下降,而重塑土的动强度曲线下降趋势则较为缓慢。

图5 湛江黏土的动强度曲线

从湛江黏土的应变与振次曲线可以看出,在不同的固结压力下,当循环动应力比σd/σ3很小时,即使荷载的循环次数很大时,土样也不会发生强度破坏,土体的累积变形很小并趋于一个稳定值,因此,能使土体发生破坏的最小动应力比即为土体的最小动强度,土体的动强度曲线随着振次的无限增大最终将趋于一条稳定曲线,低于最小动强度的动应力比不会对土体产生弱化效应,土样不会产生过大变形而导致结构损伤破坏。湛江黏土不同围压下最小动强度如图6所示,原状土的最小动强度随有效固结压力降低,衰减趋势很快,在围压大于结构屈服应力时最小动强度趋近但仍略高于重塑土,重塑样的最小动强度随围压的增加衰减缓慢。最小动强度对循环荷载作用下结构性黏土的变形发展和强度破坏有重要意义,工程中将外部动荷载设计低于土体的最小动强度,地基土就不会发生破坏。

图6 湛江黏土在不同围压下最小动强度

选取指定的破坏应变标准和破坏振次,确定不同围压下的动强度,通过莫尔圆求得土体的动强度参数-动黏聚力和动摩擦角。表3分别列出了原状土和重塑土在不同破坏振次(N=10、100、1 000)下的动黏聚力和动摩擦角。

表3可以看出,不同破坏振次N对原状土的动黏聚力cd影响不大,动内摩擦角φd随着破坏振次的减小而增大,重塑土的φd在不同破坏振次下差别不大,cd变化明显,随着破坏振次的增大动黏聚力cd减小。比较固结不排水的静三轴试验结果可知,原状土的内摩擦角φ和黏聚力cu分别为5°、75.6 kPa,重塑土的φ和cu为11.9°、14.3 kPa,结果表明,湛江结构性黏土的动强度参数中动黏聚力cd小于静强度参数之黏聚力cu,而动内摩擦角φd与静内摩擦角φ是接近的。但原状土的cd仍远大于重塑土cd,动内摩擦角则小于重塑土的φd,与静力学参数规律一致。

表3 原状土和重塑土的动强度参数

2.3 结构性对湛江黏土动孔压特性的影响

动荷载作用下饱和黏土动孔压的发展规律颇为复杂,由于孔压滞后性及测试手段有限性,主要讨论结构性对黏土的动孔压影响规律。

由图7、图8(a)中原状土在不同围压下的孔压与振次关系曲线可知,随着循环次数的增加,孔压增长规律可分为两种：①当动应力比ηd较小时,土体应变曲线为“稳定型”,土颗粒间的相互错动和位移较小,孔压上升的速率较慢,但由于振动次数较大,孔压测量的滞后效应越不显著,且累积效应导致孔压随振次不断增长,故最终的累积孔压也能达到较大值；②当动应力比ηd较大时,土体结构在振动荷载作用下处于亚稳态状态并最终会破坏失稳,故孔压增长速率快于稳定型试样的孔压曲线,但对于同为“破坏型”应变曲线的孔压-振次曲线[如图7(a)中ηd=0.9、0.95、0.98三条曲线],孔压发展速率随动应力比的增加并未明显提高,即“破坏型”应变曲线对应的孔压-振次曲线基本一致,破坏振次越大,孔压滞后效应就越小,测得土体破坏时的最终累积孔压越大。

图7 原状土在不同围压下的孔压与振次曲线

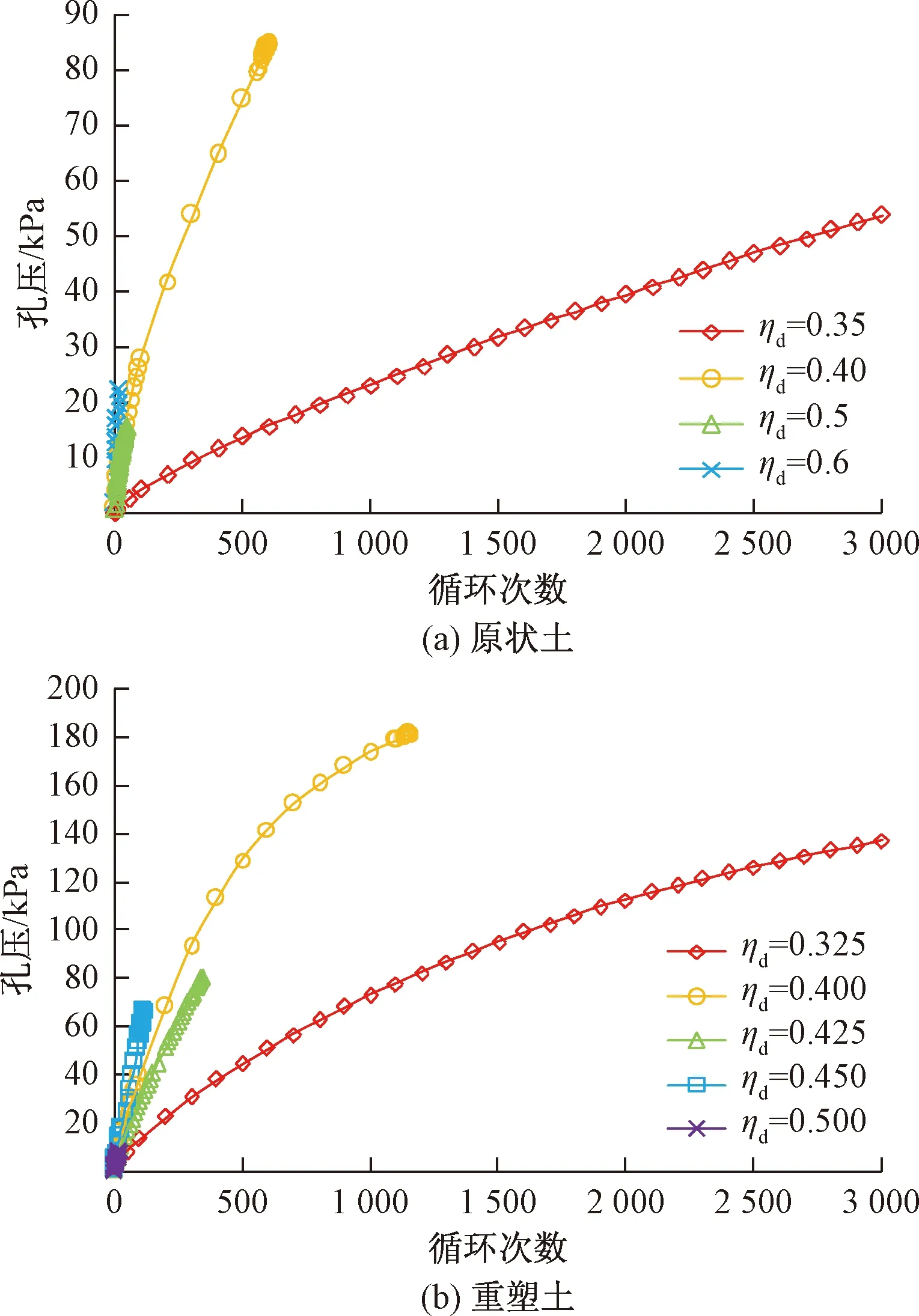
图8 原状土和重塑土的孔压与振次对比曲线(σ3=400 kPa)

由原状土的孔压-振次曲线发现,无论土体变形状态是“稳定型”还是“破坏型”,孔压随振次都呈增长势,即孔压不具有在土结构破坏时突然变化的特征,与破坏应变也没有明确的对应关系。因此,等压固结状态的动孔压-振次曲线无法反映天然土体结构的破坏特性。

对比图8的原状土和重塑土在围压σ3=400 kPa下孔压与振次关系曲线,重塑土的动应力比ηd远小于原状土的ηd,孔压却明显高于原状土,即重塑土在动荷载作用下的孔压累积效应更显著。重塑土在低于临界动应力比的小幅值循环荷载作用下,累积应变较小,孔压也会大幅增长,如图8(b)中动应力比ηd=0.325的动孔压-振次曲线,累积应变在2%左右,累积孔压高达140 kPa；同样的,当重塑土的ηd较大时,如图8(b)中动应力比ηd=0.4的孔压发展曲线,重塑土经历N>1 000次的循环荷载并振动破坏,孔压增长显著,孔压可达180 kPa。

由孔压的发展规律可知,随着循环次数的增加,原状土和重塑土的孔压均增加,但结构性对黏土的孔压特性影响较为显著,原状土颗粒之间的胶结作用阻碍了颗粒间的错动及变形,故循环荷载作用下结构性黏土的动孔压上升速率较慢。而重塑土的结构被破坏,颗粒间的联结作用基本丧失,土颗粒就容易发生较大错动,土孔压发展加快,结构性某种程度上抑制了原状土的孔压发展。

3 结论

(1)结构性黏土在循环荷载作用下呈脆性破坏特征,随固结压力增大,原状土的临界循环应力比显著下降,土体的脆性破坏特征逐渐趋于不显著,原状土的快速增长型应变曲线逐渐向重塑土的逐步增长型应变曲线发展。

(2)对于结构性黏土来说,为防止土体结构的坍塌性破坏,需谨慎选择合理的特征点作为应变破坏标准,重塑土则一般可以结合实际工况对变形的要求来确定合适的强度破坏标准。

(3)原状土和重塑土在不同围压下的动强度曲线差异性十分明显,随围压的增大,原状土的动强度曲线迅速下降,而重塑土的动强度曲线下降趋势较缓。

(4)结构性对循环荷载作用下黏土的孔压特性有一定程度的影响,原状土在动荷载作用下动孔压上升速率较慢,而重塑土在动荷载作用下的孔压累积效应更显著,结构性某种程度上抑制了原状土的孔压发展。