拉剪多轴载荷作用下的弹性梁弯曲变形
汤明刚, 郭泽鹏, 陆 晔
(中国船舶科学研究中心, 无锡 214082)
柔性管道和脐带缆是海洋资源开发中连接水面浮体与海底井口的一类重要的细长弹性体装备[1]。其在位运行过程中,顶端由于同时受到轴向拉力和弯曲载荷的作用而容易发生极限强度或疲劳失效[2],因此需要对细长弹性体进行拉弯作用下的结构响应分析[3]。考虑该装备内部多层结构的复杂性,需要采用能够模拟该复杂加载的试验模型进行研究[4]。传统的加载试验通常采用大型专用装置[5],一端施加稳定拉伸载荷,另一端通过摆动以实现管缆弯曲,尽管可以检测产品指标,但不能实现稳定的曲率分布;后续学者在摆动端添加了喇叭口装置[6],尽管可以实现稳定曲率加载,但是由于装置与细长体处处接触而影响了检测效果,因此最新的试验研究提出采用分布式多点加载技术,即稳定曲率加载通过对称横向集中剪力共同作用实现,且不影响试验效果[7]。因此为了基于该方法进行试验工况设计,需要从理论上研究细长弹性体在轴向拉伸载荷与对称横向集中剪力共同作用下的弯曲变形规律。
细长弹性体装备在有限长度内可看做是弹性梁[8],即使在小变形、平截面和线弹性假定条件下,轴向拉伸载荷的作用会引起附加弯矩,进而影响梁弯曲变形,因此梁挠度和弯矩与多轴外载荷不再呈现线性关系[9]。赵南等[10]对超大型浮体撑杆结构进行了弯剪多轴载荷作用下的响应研究,但并没有考虑轴向载荷作用的影响。王续宏等[11]通过引入阶跃系数研究轴向压缩和横向剪力作用下的柱梁变形,但是较难精确得到轴向载荷对弹性梁弯曲变形的影响。文献[12]对两端铰支跨内受均匀横向剪力的拉伸柱梁弯曲变形进行了研究,但由于均匀横向剪力与集中剪力的载荷本质与作用效果明显不同,因此无法通过对模型结果简单推导直接得到。宋文涛等[13]对不同配筋率的碳纤维增强复合材料编织网混凝土梁弯曲性能进行了试验研究,试件采用两端铰支约束,中间施加横向集中力,获取了载荷与梁曲位移的关系,但是并未提出梁弯曲变形的理论模型;张锡治等[14]采用Abaqus有限元软件对钢-混凝土预制混合梁在两端固支约束、中间施加横向集中力下的弯曲性能进行了分析,尽管获取了载荷与弯曲挠度的关系,但是并未对同时施加轴向拉力下的弯曲变形进行研究。综上可以看到,当前已有模型都无法直接获得轴向拉力载荷和横向多个集中力共同作用下弹性梁的弯曲响应规律。
1 拉剪多轴载荷下弹性梁弯曲变形解析模型
将具有一定弯曲刚度的柔性管缆试件简化为两端铰支的弹性梁,假设梁弯曲过程发生小变形、满足平截面假定,忽略轴向变形,不失一般性的施加双横向集中载荷,建立轴向拉力和横向集中力共同作用下的弹性梁弯曲模型,如图1所示。
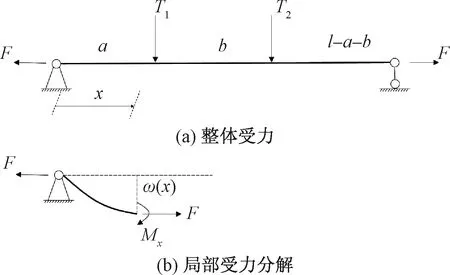
T1、T2为横向集中剪力;a为T1作用位置与原点铰支的间距;b为T2与T1作用位置的间距;l为梁总长;F为轴向力;M(x)为梁的弯矩;ω(x)为挠度
首先考虑简支梁仅受双横向集中力T1和T2的弯曲变形情况。如图1(a)所示,梁的弯矩平衡方程可以简化表示为
M(x)=Ax+B
(1)
式(1)中:A和B为代数式。设使梁下缘受拉的弯矩方向为正,分段展开式(1)可以得到:
(2)
式(2)中:EI为梁的弯曲刚度。当叠加轴向力F后,如图1(b)所示,梁的弯矩平衡方程变为
M(x)=EIω″(x)=Fω(x)+Ax+B
(3)
令n2=F/EI,则式(3)可以写为
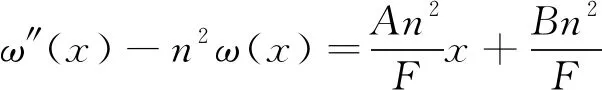
(4)
式(4)齐次微分方程通解的一般形式为:yI=C1e-nx+C2enx,取该非齐次微分方程特解:yII=-Ax/F-B/F,则式(4)的通解可以表示为
ω(x)=yI+yII=C1e-nx+C2enx+
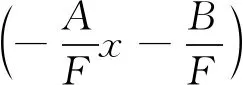
(5)
由于式(5)是分段方程,在梁的3个不同分段,其系数C1和C2是不同的,因此共有6个未知数。考虑静定梁的端部约束和连续性条件,式(5)需要满足如下6个边界条件:ω1(x)|x=0=0,ω1(x)|x=a=ω2(x)|x=a,ω′1(x)|x=a=ω′2(x)|x=a,ω1(x)|x=a+b=ω2(x)|x=a+b,ω′1(x)|x=a+b=ω′2(x)|x=a+b和ω3(x)|x=l=0。其中ωi(x)代表从梁端点沿x轴正向的第i个分段挠度。
通过联立方程组,可以解得6个未知系数如下:
式中:Cij为第i个分段内的第j个系数。将以上系数分别代入式(5)、式(3),可以得到简支梁在轴向拉力和横向集中剪力共同作用下的弯曲挠度和弯矩。
2 弹性梁弯曲变形有限元数值模型
2.1 有限元模型
采用ABAQUS结构有限元分析软件,建立考虑管道截面特性的弹性梁三维数值模型,如图2所示。采用三维Beam梁单元,赋予管道截面形状参数,材料为各项同性材料。为了同时满足管道弯曲刚度EI和截面拉伸刚度EA特性,在管道内径符合实际情况下,求解材料弹性模量和管壁厚度两个拟合参数[15]。
模型一端节点约束3个平移自由度,另一端仅放松管道轴向自由度和扭转自由度,从而实现两端铰支效果。在一端节点施加x方向集中拉伸力,而后在梁跨特定区域同时施加y方向若干横向集中力。分析采用准静态加载模块,并考虑几何大变形。考虑该有限元数值建模方法的有效性在细长柔性管道整体拉弯组合疲劳试验中得到验证[7],因此可以直接用来对本文提出的理论方法进行对比验证。

图2 弹性梁三维有限元模型
2.2 对比验证
以某195 mm内径、4 m有效长度的海洋柔性管道试件为例,弯曲刚度为120 kN·m2,截面拉伸刚度为5.04×108N,数值模型拟合材料弹性模量为 447 MPa。根据管道承载能力,轴向拉力从0施加至80 t,同时施加对称的两组1 t横向集中剪力,间隔2 m。在数值结果中直接提取梁节点的位移与弯矩。
图3显示了不同拉伸载荷下解析模型与数值模型得到的管道挠曲度对比情况。可以看出,不同拉伸载荷作用下,理论模型得到的梁曲挠度和数值模型结果总体吻合均较好,验证了解析模型的正确性。当拉伸载荷增加时,梁曲挠度逐渐减小,但分布趋势保持不变,说明弯曲变形被抑制;同时随着拉伸载荷线性增大,跨中最大挠度降幅逐渐降低。需要说明的是,数值模型由于考虑了管道轴向拉伸刚度而更趋于实际情况,因此当没有拉力作用时,其水平长度由于弯曲效应而有所减小,当拉力逐渐增加时,管道长度逐渐变长,大于理论模型4 m的长度,但总体结果分布与理论模型保持一致。
为了消除管道长度变化因素,在数值模型中提取节点弯矩并按照节点在初始位置的坐标进行弯矩分布绘制,进而与理论模型结果对比,如图4所示。可以看出,轴向拉力为0时,管道中间2 m段内曲率恒定,管道处于纯弯曲状态。当施加轴向拉力后,管道弯矩整体下降,说明拉力使得弹性梁弯矩变形减小,尤其在中间2 m段内,曲率分布呈现“凹”形态,横向剪力施加处的曲率极大,而管道中间附近曲率相对平缓。随着轴向拉力线性增大,管道曲率下降幅度逐渐降低,中间曲率越平滑。数值模型弯矩分布相对理论模型结果略微偏右,这是由于管道产生伸长变形影响所致,但是两者总体吻合很好,进一步验证了理论模型的正确性。

图3 不同拉力下梁弯曲挠度结果对比
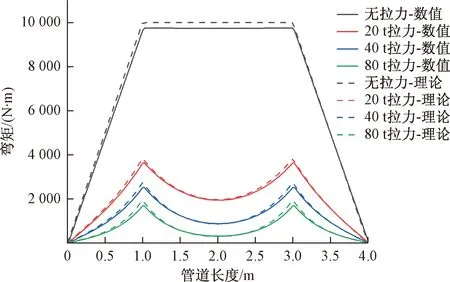
图4 不同拉力下弹性梁弯矩分布结果对比
3 弯曲变形影响因素分析
根据理论模型,除了轴向拉伸力外,影响拉剪梁弯曲变形的因素同时还包括横向集中剪力与弯曲刚度,下面以第2节相同实例进行分析讨论。
3.1 横向集中剪力影响
在轴向拉伸载荷为20 t条件下,不同横向集中剪力作用下的弹性梁曲率分布如图5所示。可以看出,随着剪力逐渐增大,梁曲率总体变大,但趋势保持一致。且随着横向剪力线性增大,其剪力作用位置极大曲率与弹性梁跨中曲率呈现线性增加,但梁跨中曲率平滑性降低。保持横向剪力不变,仅改变剪力对称分布位置,梁曲率分布变化如图6所示。当集中剪力作用间距逐渐加大,弹性梁曲率分布趋势保持不变,但是剪力作用处的曲率极大值逐渐下降,这是由于剪力对梁弯曲作用被铰支端限制所致。因此,弹性梁整体弯曲变形减小,同时跨中区域曲率分布更加平缓。
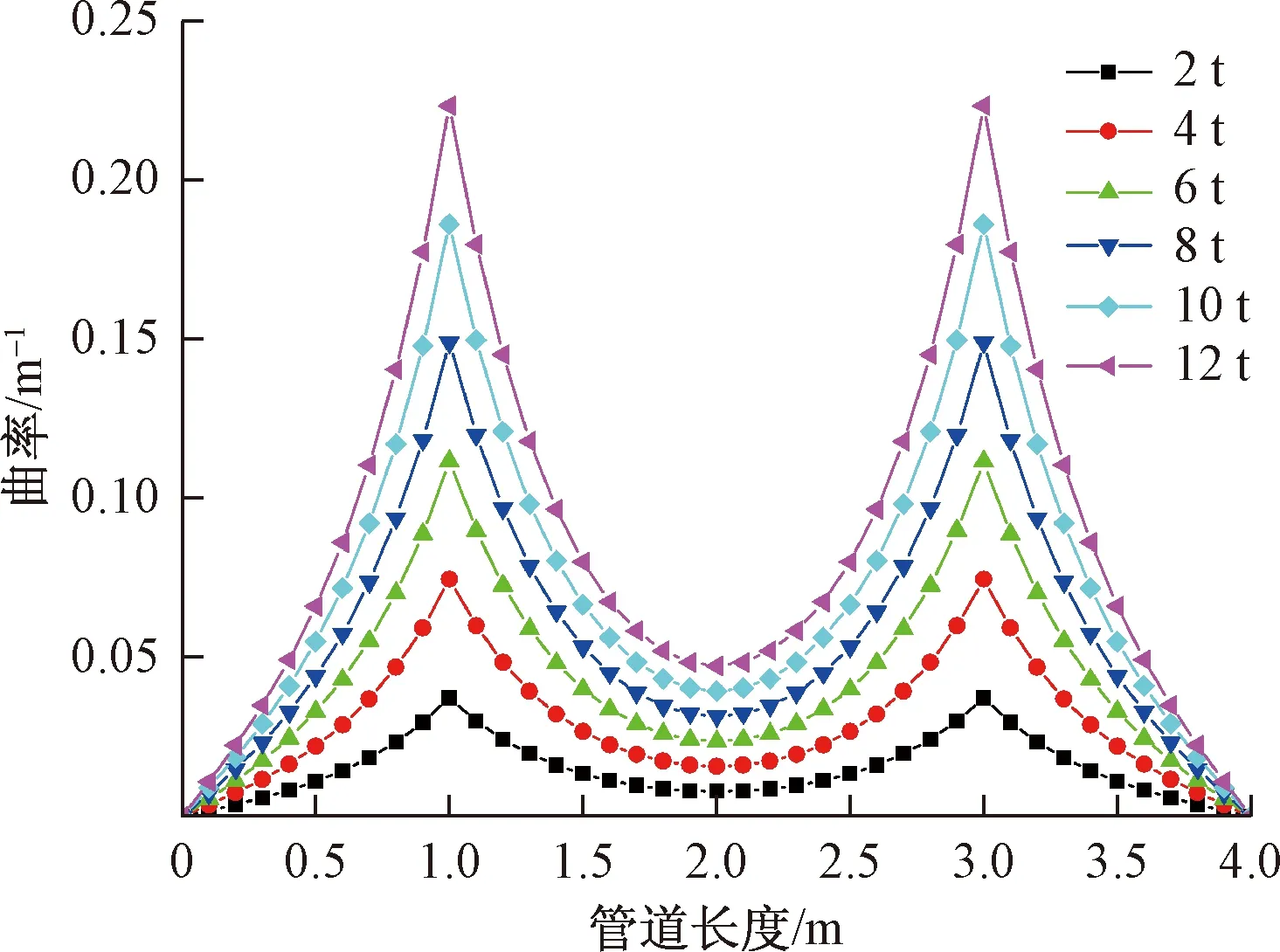
图5 不同横向集中剪力作用下弹性梁曲率分布
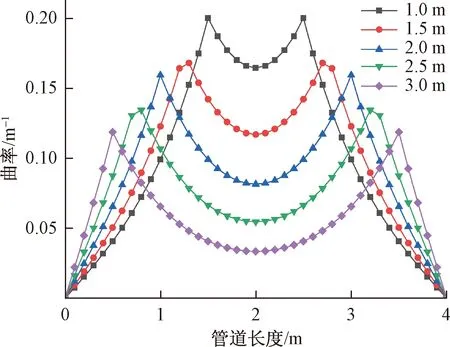
图6 不同位置横向集中剪力作用下弹性梁曲率分布
3.2 弯曲刚度影响
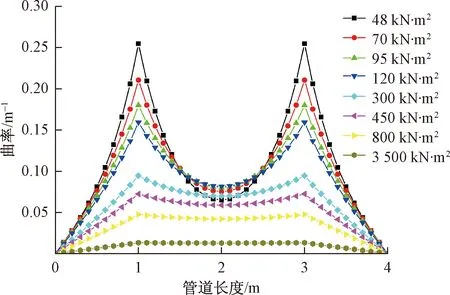
图7 不同弯曲刚度条件下弹性梁曲率分布
当轴向拉伸载荷为20 t,横向集中剪力为5 t条件下,不同量值弯曲刚度对应的弹性梁曲率分布如图7所示。当弯曲刚度逐渐增加,弹性梁曲率总体上逐渐下降,尤其是横向剪力作用处的曲率极大值逐渐下降,同时中间区域曲率的“凹”形态逐渐平缓并趋于均匀,说明相同载荷作用下弹性梁更难发生弯曲变形。值得注意的是,随着弯曲刚度的逐渐增大,跨中曲率呈现先增大后减小的趋势,与其他位置曲率变化明显不同。这是由于当梁弯曲刚度较小时,同样载荷作用下,其弯曲变形由剪力加载位置向跨中位置下降更快,“凹”形态更加凸显。因此有时为了使得弯曲刚度更小(更容易发生弯曲)的弹性梁跨中曲率更大,可能需要施加更大的横向集中剪力才能实现。
3.3 拉剪耦合影响
由于弹性梁跨中曲率通常是实际工程中所关注的,因此当弯曲刚度保持120 kN·m2不变时,得到跨中曲率随拉剪多轴载荷共同作用下的变化规律,如图8所示三维分布曲面。可以看出,当轴向拉力越大,同时横向剪力越小,弹性梁跨中弯曲变形则越小;反之,跨中弯曲变形则迅速增大。当轴向拉力不变时,跨中曲率随横向剪力基本呈现线性变化;当横向剪力不变时,跨中曲率随轴向拉力的增加而下降,且下降幅度由大变小。因此,为获取同样的柔性管道中间曲率,可以根据试验加载能力灵活调整轴向拉力与横向集中剪力的配比。
为方便工程应用,将图8所示曲面拟合为弹性梁跨中曲率κ0随轴向拉力F和横向剪力T1同步变化的经验公式[式(7)],其中:0≤F≤60 t,0≤T1≤12 t。该公式根据曲面数据分布规律,采用Gauss方程进行拟合。拟合前后的对比情况如图9所示,可以看出,经验公式获得的曲面与原始数据点之间误差较小,满足工程使用精度。
κ0=0.003 94+5.16×

(7)

图8 弹性梁跨中曲率与拉力和剪力的综合关系
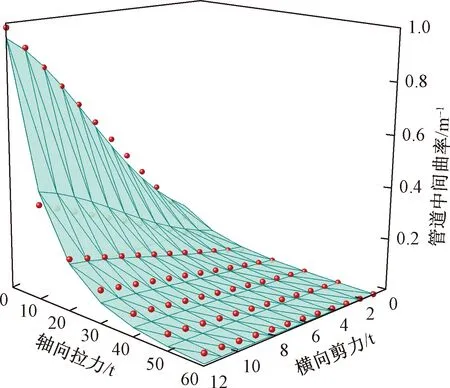
图9 拉剪作用下弹性梁跨中曲率分布拟合曲面
4 结论
推导了轴向拉伸载荷与横向集中剪力共同作用下弹性梁弯曲变形的一般解析表达式,并建立了结构三维有限元数值模型。以195 mm内径、4 m 有效长度的实际柔性管道试件为例,对弯曲变形的影响因素及变化规律进行了分析讨论,得到结论如下。
(1)由于考虑截面拉伸刚度,数值模型得到的梁曲挠度和弯矩普遍比理论结果略偏右,但是两者总体趋势和量值吻合较好,验证了解析模型的正确性。
(2)轴向拉力使得跨中区域曲率呈现“凹”形态。拉力越大,梁总体曲率越小且下降幅度渐小,跨中区域曲率分布越平滑,拉力的存在抑制了梁曲变形。
(3)横向集中剪力越小、分布越靠近铰支端,梁总体曲率基本线性减小,跨中区域曲率分布越平滑。弯曲刚度越小,由于“凹”形态加速突显,使得跨中曲率呈现先增大后减小的趋势。
(4)梁跨中曲率随拉力的减小和横向集中剪力的增大而迅速增大,将该变化规律拟合为满足工程精度的经验表达式,为柔性管道等试验加载工况的设计提供有效工具。

