谈谈高考中用“高等数学知识”和“二级结论”答题的那些事
◇ 江西 张金生(特级教师)
(作者单位:江西省南昌三中)
在高考中能否用“洛必达法则”“拉格朗日中值定理”等高等数学知识答题? 能否直接用常用的二级结论,会不会扣分? 这些一直是我们同学关心的问题.笔者多年参与高考试卷阅卷工作,现就这个问题来跟同学们聊聊.在高考中用高等数学知识解答一般不扣分,但不加证明直接使用二级结论扣不扣分要视具体情况具体分析.比如,新课改以来,导数模块成为高考的重点和热点内容,高等数学中的泰勒展开式、麦克劳林(Maclaurin)公式等是导数试题命制的一个重要题源.这些年在高考中使用“洛必达法则”“拉格朗日中值定理”等均未扣分.这里,我们来谈谈这两年高考阅卷中的几个典型案例.
例1(2020年全国卷Ⅰ理17)设{an}是公比不为1的等比数列,a1为a2,a3的等差中项.
(1)求{an}的公比;
(2)若a1=1,求数列{nan}的前n 项和.
(1)设{an}的公比为q,由题设得2a1=a2+a3,即2a1=a1q+a1q2,所以q2+q-2=0,解得q=1(舍去),q=-2,故{an}的公比为-2.
(2)设Sn为{nan}的前n 项和,由(1)及题设可得an=(-2)n-1.所以
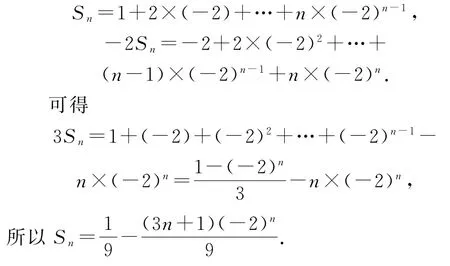
在试评中发现,有考生用二级结论:若cn=(an+b)qn-1,则{cn}的前n 项和Sn=(An+B)qn-B,其中本题cn=n(-2)n-1直接套公式得所以
该解法没有错位相减的过程,直接套用课外二级结论.经过试评组全体成员讨论,最后决定扣1分,除非证明了所用的二级结论.
例2(2018 年全国卷Ⅰ文18)如图1所示,在平行四边形ABCM 中,AB =AC =3,∠ACM =90°,以AC为折痕将△ACM 折起,使点M 到达点D 的位置,且AB⊥DA.

图1
(1)证明:平面ACD⊥平面ABC;
(2)Q 为线段AD 上一点,P 为线段BC 上一点,且求三棱锥Q-ABP 的体积.
大纲对文科生只要求了解空间直角坐标系(《必修2》),对空间向量应用不作要求,但在2018年阅卷过程中发现有几个文科考生用高等数学里的向量的混合积来解答,请看第(2)问解答过程:以C 为坐标原点的方向为y 轴正方向,建立空间直角坐标系C-xyz,则A(0,3,0),B(-3,3,0),D(0,0,3),由1),
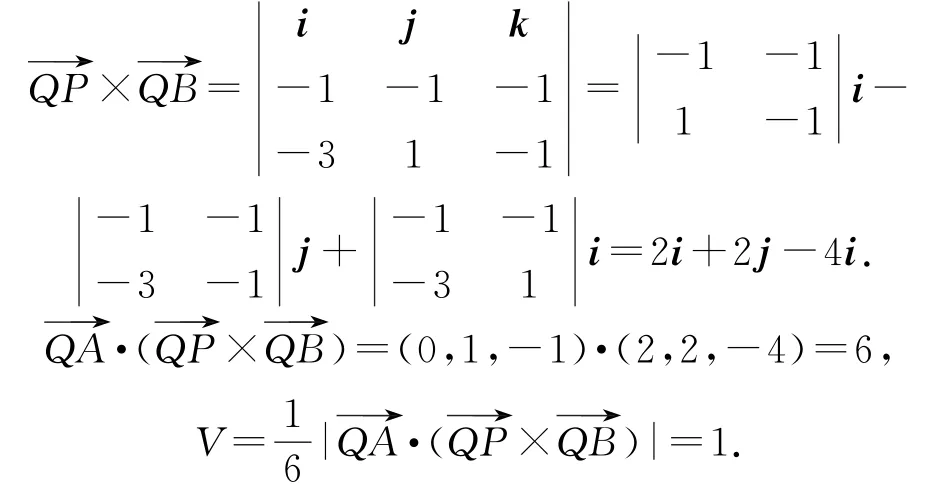
阅卷过程中发现这种应用高等数学空间解析几何的解法,解答过程完整,还是给予了肯定,没有扣分.
例3(2020年全国卷Ⅰ理20文21)已知A,B分别为椭圆的左、右顶点,G 为E 的上 顶 点为直线x=6上的动点,PA 与E 另一交点为C,PB 与E 另一交点为D.
(1)求E 的方程;
(2)证明:直线CD 过定点.
该题看似常规,但考生普遍反映很难算.根据试评结果,本题试评组给出了8种解法,常规解法之外,下面两种解法用了两个二级结论,即“椭圆上动点与长轴两端点连线斜率之积为定值”“椭圆上动点与中心对称两点连线斜率之积为定值”,开拓了解题思路,简化了运算.

一些对数学有浓厚兴趣的同学,自学了高等数学知识,碰巧在高考时用上了,这是值得肯定的.在解答步骤多的计算题中穿插了“二级结论”通常也不扣分.掌握一定的典型的课外二级结论,结合解题技巧是解题灵活性的表现,也直接影响着运算的快捷程度.在学习过程中不断地对典型试题寻本探源、总结反思、积累经验,总结出“二级结论”和一点解题小窍门、小技巧是必要的.但过于热衷 “秒杀”,死记太多 “二级结论”,把数学思维活动变成死记硬背,这不可取.

