高中数学解题的基本方法
———以函数与方程为例
◇ 山东 梁桂媛 李爱霞
(作者单位:山东省青州第一中学)
在解题过程中,数学思想和基本方法是解题的关键之处和灵魂所在.掌握好数学思想,解题就能如鱼得水,从而达到事半功倍的效果.所以高中数学教师在讲解新课的时候要注重对数学思想和数学解题方法的渗透,在上习题课的时候注重对数学解题方法的总结,从而帮助学生建立数学解题基本方法的框架,在解题时有规律性和条理性,提高解题的正确性.
1 配方法
配方法的主要思想是对题目中给出的关系式进行变形,得到已知条件和未知条件之间的数量关系.在使用完全平方式的时候需要注意,如果题目的已知条件或未知条件中含有一元二次函数、一元二次方程或是一元二次不等式,可以依据完全平方公式通过加项或减项的方式进行变形,最后得到完全平方的形式,达到“化繁为简”的目的.
例1若方程x2+y2-4kx-2y+5k=0 表示圆,则k 的取值范围是多少?
将圆的一般方程x2+y2-4kx-2y+5k=0化为圆的标准方程
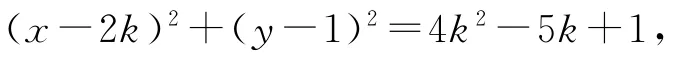
该方程表示圆,需要满足4k2-5k+1>0,从而可以通过因式分解进行求解,将4k2-5k+1>0化为
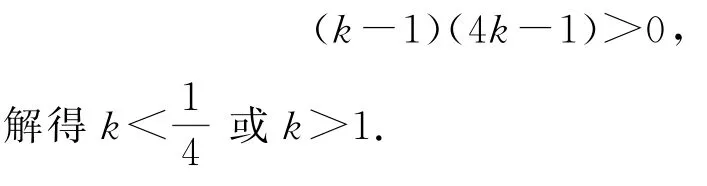
2 换元法
在解题的过程中,换元法也是我们经常应用的一种方法,换元法的主要思想是在一道数学题目中,把某个式子看作一个整体,在解题过程中,用一个简单的变量代替一个复杂的式子,达到“化繁为简”的目的.在换元的过程中,我们应该遵循的原则为“化繁为简”,尽量将一般式化为标准式.在解题的过程中,需要特别注意的一点是进行换元后,要注意新元的取值范围.
例2设实数x 和y 满足x2+2xy-1=0,则x+y 的取值范围为________.
x2+2xy-1=0可化为-x2+2x2+2xy-1=0,即x2-2x2-2xy+1=0,故可以得到x2-2(x+y)x+1=0.
将x+y=k 代入上式,可以得到x2-2kx+1=0,此时等量关系式变为含有未知量x 的一元二次方程,若方程有解,则需要满足Δ=b2-4ac≥0,即
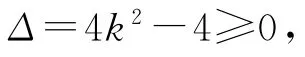
解得k≤-1或k≥1.
3 待定系数法
在有些数学题目中,我们需要确定自变量和因变量之间的函数关系,此时需要预先设出自变量,然后根据题目中的条件,列出含有未知系数的关系式,最后根据题目中给出的已知条件,列出关于待定系数的等量关系式,再求解待定的系数.
例3已知直线l的表达式为2x+3y+5=0,假设存在一条直线m 与直线l 平行,并且直线m 过点(1,-4),求直线m 的表达式.
因为直线m 与直线l平行,所以可设直线m的表达式为2x+3y+c=0,又因为直线m过点(1,-4),则将点(1,-4)代入2x+3y+c=0中,得2×1+3×(-4)+c=0,解得c=10,即求得直线m 的表达式为2x+3y+10=0.
4 定义法
定义法也是我们在解题的过程中常常应用的一种方法,在讲解新知识的时候,教师都会从定义开始讲起,只有把握好定义,才能为后面的学习奠定良好的基础,所以定义是解决问题的根本,利用定义进行解题,就是我们常常说的定义法解题.
例4证明:函数f(x)=-x3+1 在(-∞,+∞)上是减函数.
证明设∀x1,x2∈R且x1<x2,可知
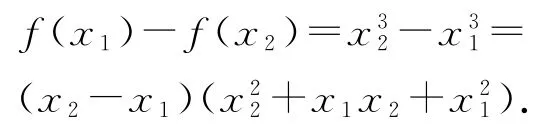
因为x1<x2,得到x2-x1>0,且在x1与x2中至少有一个不为0,不妨设x2≠0,故
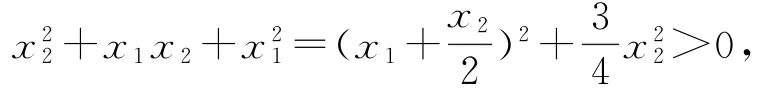
所以f(x1)>f(x2),故f(x)在 (-∞,+∞)上为减函数.

