新交规下路段无信号控制人行横道人车让行率估计方法研究

董洁霜，杨城城，王嘉文 DONG Jieshuang, YANG Chengcheng, WANG Jiawen

（上海理工大学 管理学院，上海200093）

(School of Management, University of Shanghai for Science and Technology, Shanghai 200093, China)

0 引 言

人车让行率是指当车辆和过街行人同时拥有通行权时，礼让行人优先通过的车辆占人车交互次数的比例，这里的人车交互是指车辆与过街行人之间：（1） 车让人同时人让车，（2） 车让人，（3） 人让车，（4） 人不让车同时车不让人这四种情形发生的过程。随着城市路网车辆的日益增多，过街行人安全越来越受到交通管理部门的重视，2016 年《中华人民共和国道路交通安全法》第四十七条规定：“机动车遇行人正在通过人行横道应当停车让行；机动车行经没有交通信号的道路时，遇行人横过道路应当避让”，“车让人”已由一种理念转变为具有强制性的交通法规。

目前，国内外对人车交互的相关研究主要分为两方面：人车交互的影响因素和人车交互对交通产生的影响。

（1） 对人车交互影响因素的研究主要从以下三方面展开：①行人方面：Kimberly[1]研究了种族和性别对驾驶员让行行为的影响，结果表明在人行横道处驾驶员倾向于不为黑人和男性行人让行。②车辆方面：驾驶员是让行行为决策做出的一方，目前对车辆的研究主要集中在流量和速度方面。窦水海[2]研究表明，随车流量和车速的增加让行率有所下降。③交通环境方面：Stapleton[3]研究了道路设施对让行率的影响，结果表明在增加了矩形信号指示灯的交叉口，让行率会显著提升。

（2） 让行率对交通产生的影响主要从以下三方面展开：①通行能力方面：Wei Dali[4]建立了行人绝对优先情况下通行能力计算公式，此公式虽考虑了行人因素，但模型假设条件过于理想，与实际相差较大。②延误方面：Zheng[5]建立了基于人车交互的行人延误模型，此模型缺乏对让行率动态变化特征的考虑。③信号配时优化方面：张凌煊[6]研究了考虑行人的交叉口配时优化，建立了交叉口多目标信号配时优化模型，此模型虽考虑了行人因素，但仍不能反映让行率变化对交叉口信号配时的影响。

对于人车交互问题，国内外学者虽然在人车交互影响因素和人车交互产生的影响两方面进行了一定研究，但定量研究让行率的文献几乎没有，所以笔者以此为切入点，运用主成分分析法与Logit 模型对让行率进行定量研究。

1 让行率影响因素

1.1 行人决策影响因素。根据前人研究，人车交互时行人选择通过与否时考虑的因素有车流量[2]、车速与道路宽度[3]、车辆种类[2]、车辆与行人的距离[5]、人行横道几何因素[3]、行人流量[5]、行人特征[1]、光线强度及监控设施[3]的有无。以下通过问卷调查分别对其中的车辆种类、行人种类与光线强度三种因素进行了影响程度划分和量化描述：

车辆种类：人车交互时车辆种类会对行人决策产生影响。研究中将机动车分为小汽车、中型车和大型车三类，根据李克特五分量表将行人对三种车型的危险感知程度进行分值为1-5 五级划分设计调查问卷，在上海市杨浦区延吉东路—松花江路、安

图路—靖宇东路交叉口处对行人发放并现场收回。通过问卷调查得到行人对不同车种的感知危险程度：小汽车1.36、中型车2.40 和大型车3.90。以小汽车为标准，得到各类车辆相对于小汽车的危险程度：1.00、1.76 和2.88。本文引入车辆特征系数概念表示车种对行人决策的影响，其计算方法如下：

其中：kv为车辆特征系数，1.00≤kv≤2.00；nvb、nvv、nvc和nv分别为大、中、小汽车及所有车的数量（veh/h），nvb+nvv+nvc=nv。

行人特征：人车交互时不同行人会对车辆决策产生影响[1]。与车种因素研究类似，得到驾驶员对青年、中年及老年人的让行意愿分别为1.00、1.80 和2.35。本文引入行人特征系数概念表示行人特征对驾驶员决策的影响，其计算方法如下：

其中：kp为行人特征系数，1.00≤kp≤2.35；npt、npa、npo和np分别为行人中青年、中年、老年人及所有人的数量（ped/h），npt+npa+npo=np。

光线强度：光线强度也会对人车决策产生影响[3]。与车种因素类似，经调查取人车交互在白天、傍晚和夜间的光线值分别为3、2 和1。

由于以上各因素对行人决策的影响程度不同，加之部分因素结论的得出所使用的方法不是定量方法，因此有必要对影响因素进行相关性分析。研究中采用Pearson 分析法进行相关性分析，过程如下：

选取上海市杨浦区敦化路、营口路、松花江路和延吉东路四条具有无信号控制人行横道的路段，于2019 年5 月16 日通过视频观测得到各路段10 组实际数据如表1 所示。对表1 中的数据进行Pearson 相关分析，结果表明：车流量、车速、车辆种类、车辆与行人的距离、人行横道长度以及过街行人流量的显著性（双尾） 水平小于0.05，即这些因素与行人决策有显著相关关系，在满足显著性水平小于0.05 的前提下，分析结果中Pearson 相关性的绝对值表示某因素与行人决策关系的强弱程度，正负值表示正负相关。

表1 行人车辆决策影响因素观测数据

此外，由于各因素之间还可能相关，因此需进行变量之间的相关性分析，并将这些因素转变为独立变量，研究中基于主成分分析法使用SPSS 软件进行变量间的相关性分析。

经主成分分析原始因素中的信息保留了68.357%，已提取了绝大部分信息；影响行人决策的因素已由原来相关的7 个抽象为相互正交的2 个主成分：F1p和F2

p，其分别由原来7 个原始因素经标准变换后的值线性表示。此外，与第一主成分较密切的因素是人流量、人车距离与车流量，相关系数分别为0.900、0.808 和0.735；与第二主成分较密切的因素是人行横道长度、车速，相关系数分别为0.631 和0.627，相对于第二主成分，第一主成分各指标间相关性较强。

行人决策主成分表达式为：

其中：Fip（i=1,2）为影响行人决策的主成分，xj（j=1,2,…,7）为行人决策影响因素标准值。

1.2 车辆决策影响因素。与行人决策影响因素分析类似，影响车辆决策的因素包括车流量、车速、道路宽度、车辆种类、车辆与行人的距离、人行横道长度、人行横道宽度、行人流量、行人特征、光线强度以及监控设施的有无。采用Pearson 相关分析法进行相关性分析。结果表明车流量、车速、车辆与行人的距离、人行横道长度、行人流量以及行人特征系数的显著性（双尾） 水平小于0.05，即这些因素与车辆决策有显著相关关系。

经主成分分析原始因素中的信息保留了80.193%，已提取了绝大部分信息；影响车辆决策的因素已由原来相关的8 个抽象为相互正交的3 个主成分：F1v～F3v，其分别由原来8 个原始因素经标准变换后的值线性表示。此外，与第一主成分较密切的因素是车流量、人车距离、人行横道长度及人流量，相关系数分别为0.810、0.811、0.802 和0.812；与第二主成分较密切的因素是车速，相关系数为0.785，与第三主成分较密切的因素是行人特征系数，相关系数为0.861。相对于第二、三主成分，第一主成分各指标间相关性较强。

车辆决策主成分表达式为：

式中：Fiv（i=1,2,3）为影响车辆决策的主成分，yj（j=1,2,…,8）为车辆决策影响因素标准值。

2 人车交互Logit 模型

2.1 行人决策模型。当过街行人遇到车辆时，等待与通过的决策本质上是一个离散选择行为，即从两种过街方式中选择“效用”最大的一种，本文采用Logit 模型建立行人过街决策分担率模型，Logit 模型如下：

式中：Pp（i）（i=1,2）为行人选择通过与否的概率（0≤Pp（i）≤1）；为行人决策效用函数。

效用函数确定：以影响行人决策的主成分作为效用函数自变量，给出表达式：

式中：θi、μi为主成分权重系数，ai为常数项。

权重系数确定：对式（7） 变形并以1.1 中观测数据对权重系数进行回归。首先将数据标准化并代入式（3）、式（4） 得到影响行人决策的主成分F1p和F2p，再通过F1p、F2p及行人选择通过的实测概率对权重系数进行回归，得到系数θ2-θ1、μ2-μ1及a2-a1的值分别为-0.420、0.089 和-1.502。此外，回归分析截尾概率为2.32E-8，接近于零，且从残差与变量关系图中可知残差与自变量没有关系，即残差独立，回归方程成立。

回归系数得到：

2.2 车辆决策模型。与行人决策模型类似，车辆决策Logit 模型如下：

式中：Pv（i）（i=1,2）为车辆选择通过与否的概率（0≤Pv（i）≤1）；Uiv为车辆决策效用函数。

效用函数确定：以影响车辆决策主成分作为效用函数自变量，给出表达式：

式中：αi、βi与γi为主成分权重系数，bi为常数项。

与行人权重系数确定类似，得到α2-α1、β2-β1、γ2-γ1及b2-b1值分别为0.319、-0.084、0.143 及1.550。

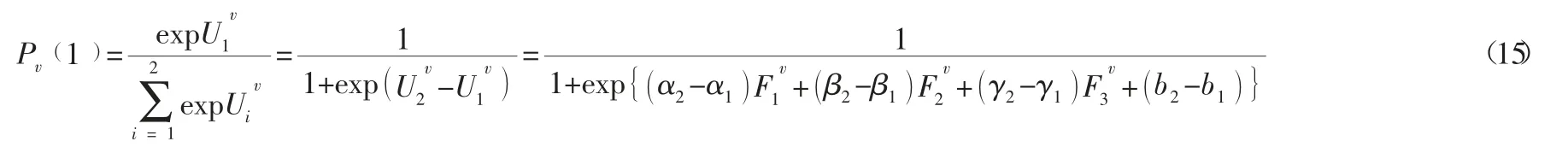
回归系数得到：

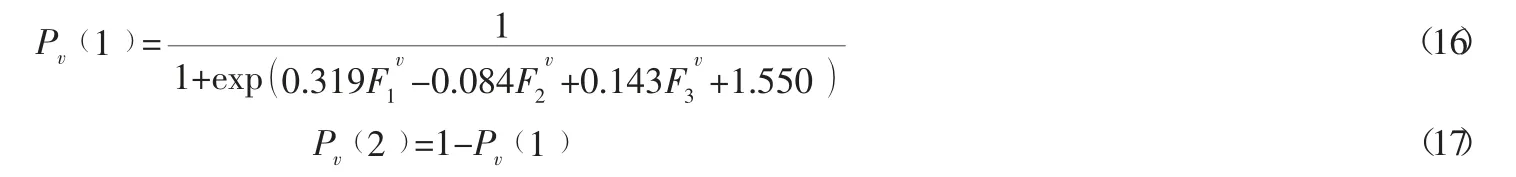
2.3 结果分析。由于行人决策与车辆决策相互独立，因此当得到行人与车辆选择通过的概率后，便可得到以下情形发生的概率如表2 所示。

表2 人车交互四种情形及发生概率

四种人车交互情形中，（2） 是交通法规所要求的，既能体现驾驶员交通文明程度，又能增加行人过街安全；（3） 虽是一方通过一方让行，一定程度上可减少人车直接冲突，但不符合以人为本的交通理念；（4） 最为不利，此情形下很可能会发生交通事故；（1） 虽然在很大程度上能保证人车安全，但也降低了通行效率，且在下一决策时刻可能演化为（4）。综上，（2） 的概率应尽可能提高，其他三种情形的概率应尽可能降低。

在实际中，不同人车交互情形对应的概率会随影响人车决策因素的变化而改变，因此，合理的交通管理应当能够使影响人车决策的正向因素增大，负向因素减小，从而使（2） 发生的概率增大，其它情形的发生概率减小，以改善人车交互时车辆与行人的安全、提高人车交互的效率。

3 模型验证

为验证模型的正确性，以上海市杨浦区靖宇东路公安局处和安图路杨浦区中心医院处无信号控制人行横道为例，于2019年5 月28 日通过视频观测得到10 组影响人车决策的实测。将观测数据标准化后，将其分别代入式（9）、式（14） 得到各组影响人车决策的效用值，再将效用值分别代入式（11）、式（16） 即可得到人与车选择通过的概率计算值Pp（1）、Pv（1）。

行人与车辆选择通过的计算概率与实测概率对比图如图1、图2 所示，图1 表明在此路段观测时间内，行人决策实测概率与计算概率曲线基本重合，即模型计算概率与实测概率的误差较小，经计算两者的平均、最大与最小误差分别为6.9%、12.0%和1.0%；类似的，图2 中车辆决策实测概率与计算概率的平均、最大与最小误差分别为5.6%、15.0%和2.0%。理论与实际存在误差的可能原因是：①模型中对行人差异进行了3 类划分，而实际中行人还有心理和教育背景等其他差异；②模型虽然考虑了诸多影响人车决策的因素，但实际的影响因素可能更为复杂，例如还可能包括天气等因素。

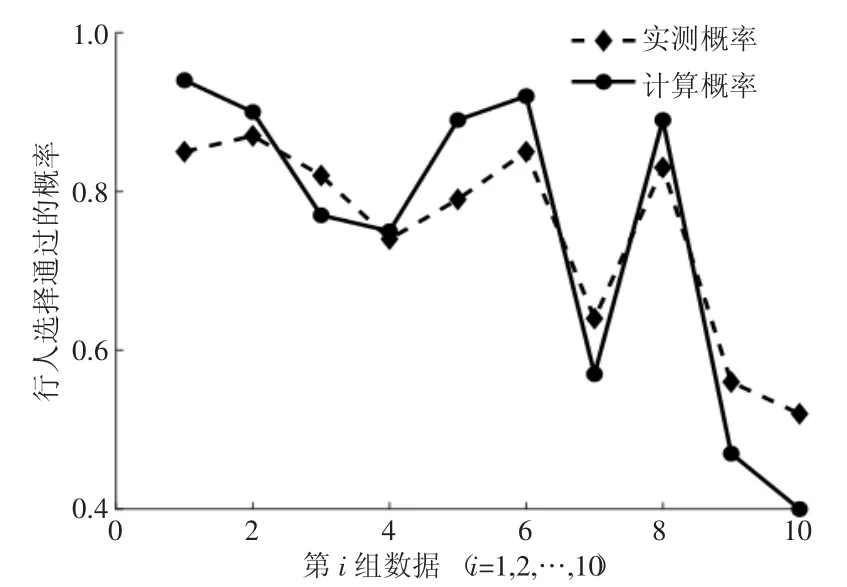
图1 行人通过的计算概率与实测概率对比

图2 车辆通过的计算概率与实测概率对比

以下根据模型所得行人与车辆的选择通过概率计算人车交互时四种情形的概率（如表3 所示）：

表3 四种人车交互情形概率计算值

结果分析：该路段情形（1） ～（4） 出现的概率平均值分别为0.13、0.61、0.08 和0.13，即该路段车让人概率较大，其余三种情形概率均较小（小于0.20），因此总体而言，该路段人行横道处人车交互状态尚可，即在具有较高安全度的同时运行效率也较高。此外，表3 中第9、10 组数据情形（2） 的概率明显较其他组小，分别为0.27 和0.23；情形（1） 概率明显较其他组大，分别为0.31 和0.34，出现这种现象的原因可能是第9、10 组数据采集的时间为21:00～23:00，虽然人流量与车流量较白天少，但因光线较暗，驾驶员与行人更倾向于保守的人车交互方式，即牺牲一定效率的同时增加了行人与车辆的安全。当交通管理部门致力于提高夜间的人车交互效率或因人车流量增加而必须提高人车交互效率时，采取的措施可以是采用亮度更高的路灯，以增加此路段夜间的光线强度。

4 结论与展望

本文对城市路段无信号控制人行横道处人车交互的影响因素做出了总结，运用相关性分析法和主成分分析法对主要因素进行提取，基于Logit 模型建立了人车交互Logit 概率模型，并以上海市两处人行横道为例，验证了模型的有效性。研究得出了以下结论：（1） 影响车辆让行与否的主要因素有车流量、平均车速、车辆与行人的距离、人行横道长度、行人流量、行人种类、光线强度、交通监控设施的有无。影响行人通过与否决策的主要因素有车流量、平均车速、车辆种类、车辆与行人的距离、人行横道长度、行人流量、光线强度。（2） 建立了路段无信号控制人行横道人车交互概率估计模型，并通过实例验证了模型的有效性。通过该模型可得到特定无信号控制人行横道处人车相遇时互不礼让的概率，即出现危险情形的概率，此概率可作为交通管理部门减少安全隐患与改善路段无信号控制人行横道处安全的依据。此外，此模型可作为通行能力计算模型中过街行人对车流影响的定量依据，从而为道路动态通行能力的估计提供了借鉴。（3） 本文所提出的人车交互Logit 概率模型适用范围仅限于行人到达服从泊松分布的情况，实际中人车交互现象还普遍存在于交叉口不受控制右转车流与过街行人之间，存在于左转车流与待转入道路过街行人之间，当这些交叉口对行人过街进行信号控制时，行人的到达将不再服从泊松分布，这些方面值得进一步研究。