基于大型直剪试验的土石混合体剪切强度特性及剪切变形模拟方法研究

罗亚琼， 张超， 马婷婷

(1.重庆科创职业学院 建筑工程系， 重庆市 402100； 2.湖南科技大学 岩土工程稳定控制与健康检测湖南省重点实验室； 3.重庆市渝北职业教育中心)

1 引言

土石混合体作为一种路基填料广泛应用于山区道路建设。土石混合体颗粒特征与土体、岩体相比具有复杂多样性和分布不均匀性，使填筑路基出现过大变形而发生剪切破坏，因此，为了使土石混合体填筑路基能够满足工程正常使用要求，土石混合体剪切强度特性及剪切变形模拟方法研究具有重要的理论意义和工程价值。

非连续非均质性使土石混合体剪切强度特性变得非常复杂，土石混合体含水量、含石量和颗粒级配等参数确定方法在路基填料设计中缺乏相应规范指导。由于直剪试验较贴近工程实际，具有可操作性强及经济的特点，被众多学者用于土石混合体剪切强度特性研究。为此，很多学者基于现场原位水平推剪试验和室内大型直剪试验对土石混合体剪切强度特性进行了研究，这些成果为路基填料设计提供了一定的参考依据。然而，当控制单一变量研究各因素对土石混合体剪切强度特性的影响规律时，试验次数呈指数增长使工作量剧增，同时，土石混合体与砂土材料在颗粒特征方面存在明显不同，仍采用黏聚力和内摩擦角表述土石混合体剪切强度特性具有一定的缺陷与不足。由于剪应力与剪切位移关系曲线是土石混合体剪切强度特性研究的参考依据，因此，土石混合体剪切变形模拟方法成为了土力学中研究的热点问题之一。G.W.Clough采用类似邓肯张模型建立能够反映应变硬化的双曲线剪切本构模型；C.S.Desai等和张嘎等基于损伤理论建立了能够在一定程度上反映应变软化的剪切损伤本构模型。然而，上述模型将剪切带的平均剪应变作为剪应变的度量方法，而剪切带厚度尚无可行的计算方法甚至有些岩土材料在剪切变形时不存在剪切带，由此将使剪应变数值出现无穷大的情况，显然与实际不符。为此，曹文贵等将剪应变替代为剪切相对位移，引入损伤理论建立了能够反映结构面与接触面间应变软化的剪切本构模型，但该模型是完全依赖应变等价性假设建立起来的，无法很好地阐释土石混合体剪切强度特性。

综上所述，为了研究土石混合体剪切强度特性及剪切变形模拟方法，该文首先考虑含水量、含石量、土性和岩性等因素，采用正交设计试验方法，对受多因素、多水平影响的土石混合体开展大型直剪试验，分析土石混合体剪切强度特性，建立抗剪强度指标合理表述方法，然后通过分析土石混合体剪切变形特征及剪切强度特性，引入损伤理论对基于应变等价性假设建立的损伤模型进行修正，进而建立能够反映土石混合体应变软化的剪切损伤本构模型，以期完善土石混合体变形力学性质研究的理论与方法。

2 土石混合体大型直剪试验

2.1 试验设备

土石混合体大型直剪试验研究设备主要包括大型直剪试验机、台秤、自动筛分机、烘箱和喷水壶等。直剪试验采用美国S2450型大型直剪试验机，仪器主要由水平加载系统、法向加载系统、长宽高为300 mm×300 mm×150 mm的剪切盒(上、下盒各高75 mm)和数据采集系统等组成。通过固定位移计和上剪切盒并由法向加载系统提供设定的法向应力，然后由液压缸提供剪切力水平移动下剪切盒，采用恒压微调阀实现应变率的无级变化，由数据采集终端系统实时生成土石混合体的剪应力与剪切位移关系曲线。

2.2 试验方案

以湖南省某山区高速公路土石混合体路基填料为研究对象，现场选取黏性土和角砾，同时，为了研究土性和砾性对土石混合体剪切强度和变形特性的影响规律，增加无黏性土和圆砾等掺量。土石混合体填料的不均匀系数Cu和曲率系数Cc等参数均需满足级配良好要求，因此，试验方案主要考虑含水量w、含石量P5、土性和砾性4种因素对土石混合体剪切强度特性的影响规律。

含水量(w)因素：考虑山区路基处在旱涝极端环境中且路基填料含水量最优宜压实阶段，该文将含水量设定为4个水平，即0、4%、7%、饱和。

含石量(P5)因素：大型直剪仪适用最大控制粒径为40 mm，土石粒径界限为5 mm，超过40 mm的路基填料采用5～40 mm等质量替代。考虑到含石量决定土石混合体骨架结构形式进而对剪切强度特性产生重要影响，该文将含石量设定为4个水平，即25%、40%、55%、70%。

由此可见，要获得多因素作用下土石混合体抗剪强度特性所需的全面试验方案为42×22=64种，每种方案又需在至少4种法向应力作用下进行直剪试验，可以看出试验工作耗时较长，需对试验方案进行科学合理的设计。为此，采用正交设计试验方法可得到受多因素、多水平影响的土石混合体试验方案，如表1所示。由表1可以看出：土石混合体正交试验方案有16种，仅为全面试验方案(64种)的25%，试验次数明显缩小。

表1 土石混合体正交试验方案

2.3 试验过程及结果

根据各编号正交试验方案的试验参数配制重量相等的土石料并充分拌和均匀，分4层装入上下均垫有5 mm厚透水板的剪切盒中进行土石混合体固结试验，结束标准为每隔1 h试样法向变形不超过0.01 mm。设定法向应力分别为150、200、250、300 kPa，控制剪切速率为3 mm/min，对土石混合体试样进行直剪试验，结束标准为剪切位移36 mm(试样长度12%)或出现残余剪应力。

土石混合体大型直剪试验结束后，根据数据终端采集系统可获得各编号试验方案在4种不同法向应力作用下土石混合体剪应力与剪切位移关系曲线，限于篇幅该文仅给出方案编号为1#的试验曲线，如图1所示。

3 土石混合体剪切强度特性

通过观察土石混合体剪切破坏面，可知试样剪切

图1 剪应力与剪切位移关系曲线(1#方案)

面呈明显的凹凸起伏状而非光滑平面状，颗粒相互交错镶嵌排列，存在砾石破碎、转动和翻转，甚至砾石剪断的现象。由此可见，土石混合体剪切破坏面并非土石颗粒表面摩擦的理想剪切平面，这显然与土石混合体含有不同粒径的砾石有关，因此，土石混合体剪切强度来源并不仅是颗粒表面内摩擦力，还存在颗粒相互交错镶嵌形成的咬合力，从而使土石混合体剪切强度得到较大提高，这与砂土材料剪切强度来源存在明显差异。因此，该文建议将土石混合体抗剪强度准则表述为：

τ=c+σtanφ

(1)

式中：τ和σ分别为剪应力和法向应力;c和φ分别为结构力和摩阻角。

尽管式(1)与摩尔库仑强度准则形式相似，但两者抗剪强度指标在物理含义和数值特征方面均存在显著差异，于是，该文分析各因素对结构力和摩阻角的影响规律。

由SL 237-1999《土工试验规程》可知：抗剪强度应取剪应力与剪切位移关系曲线上的峰值应力，若无明显峰值则取剪切位移为试样长度10%处的剪应力。于是，基于式(1)对土石混合体大型直剪试验曲线进行处理，可得各编号试验方案的抗剪强度指标，如表2所示。

采用正交设计分析方法研究各因素对土石混合体抗剪强度指标的影响规律，需对各因素的水平进行标号。对于因素为含水量和含石量，其水平均按数值由小到大依次标号为1、2、3和4；对于因素为土性和砾性，其水平按无黏性和黏性、原状和角状均分别标号为1和2。现举例说明计算含石量为25%(标号1)下土石混合体的结构力和摩阻角，首先，根据表1查出含石量为25%的方案编号，即1#、5#、9#、13#；然后，根据这些编号查出表2相应的结构力和摩阻角；最后，根据式(2)、(3)计算出该因素处于该水平下的抗剪强度指标均值。其余指标计算依此类推。

表2 土石混合体抗剪强度指标

c1=(2.41+2.33+5.68+1.68)/4=3.03 kPa

(2)

φ1=(32.19+35.76+27.93+28.44)/4=31.08°

(3)

Rφ=max(φ1,φ2,φ3,φ4)-min(φ1,φ2,φ3,φ4)

(4)

Rc=max(c1,c2,c3,c4)-min(c1,c2,c3,c4)

(5)

采用上述方法可得各因素各水平在正交设计试验方案中的抗剪强度指标均值，在此基础上计算各因素对抗剪强度指标影响程度的极差值，如表3所示。

表3 抗剪强度指标均值及极差值

由表3可以看出：

(1) 各因素对摩阻角和结构力的影响程度按由高到低的顺序分别为含石量>含水量>砾性>土性，砾性>含水量>含石量>土性。土石混合体抗剪强度主要来源于粗颗粒间相互嵌入、咬合以及相互摩擦，因此，在路基填料设计中需优化含石量和含水量等关键参数，使土石混合体形成完整土石骨架结构以提高土石混合体抗剪强度。

(2) 土石混合体抗剪强度指标由土、石料性质共同决定，各因素对土石混合体抗剪强度指标的影响规律存在显著差异。摩阻角随着含石量增大而增大，但随着含水量增大呈先增大后降低的变化规律；结构力受到各因素的影响程度较弱。

(3) 提高含石量能够增大粗、细颗粒间的接触面从而增大粗、细颗粒间咬合力和摩擦力。含水量对土石混合体抗剪强度增强效应存在最优值，含水量过低，不利于土石混合体密实，含水量过高，水的润滑效应明显，对土石混合体抗剪强度起弱化作用。

前述已获得了土石混合体剪应力与剪切位移关系曲线，在此基础上建立土石混合体抗剪强度准则并获得各因素对结构力和摩阻角的影响规律。下文将在土石混合体大型直剪试验基础上建立土石混合体剪切变形过程模拟方法。

4 土石混合体剪切变形模拟方法

4.1 土石混合体剪切变形特征

根据不同法向应力作用下土石混合体剪应力与剪切位移关系曲线，可知方案编号为1#土体混合体剪切破坏模式为应变软化型，概述如下：

(1) 土石混合体剪切过程分别经历线弹性、应变硬化、应变软化和残余强度等变形阶段。

(2) 随着法向应力增大，土石混合体剪切刚度不断增大，屈服应力、峰值应力和残余应力及其分别对应的屈服应变、峰值应变和残余应变均增大。

土石混合体剪切变形特征与三轴压缩试验条件下岩石轴向变形特征基本类似，均呈阶段性变形特征。岩石统计损伤本构模型研究已取得了显著成果，该类方法虽然是针对连续性固体材料提出的，但为该文建立土石混合体剪切损伤模型提供了一条值得借鉴的途径。为此，该文将在此基础上探讨土石混合体剪切变形破坏全过程模拟方法。

4.2 土石混合体剪切损伤模型

目前，得到广泛应用的损伤模型是基于应变等价性假设建立的，即：

σi=σ′i(1-D)

(6)

式中：σi和σ′i分别为岩土材料所受的名义应力和有效应力；D为损伤变量。

该损伤模型虽然在反映岩土材料应变软化特征方面具有明显优势，但它认为损伤意味着岩土材料内部将形成不具有任何承载能力的空隙，这使该损伤模型无法反映岩土材料残余强度变形阶段特征。为此，许多学者延续采用应变等价性假设建立损伤模型的思路不断进行改进，建立了能够反映岩土材料残余强度变形阶段特征的损伤模型。然而，应变等价性假设尚未完全得到科学合理的验证，也无法从微观力学角度分析岩土材料的损伤破坏机制，使这些损伤模型存在一定缺陷与不足。为此，该文引入损伤力学理论对土石混合体剪切损伤破坏机制进行分析以修正应变等价性假设，进而建立能够反映土石混合体剪切变形特征的剪切损伤模型。

根据损伤力学理论可推知基于应变等价性假设的土石混合体剪切损伤模型，即：

τ=τ′(1-D)

(7)

式中：τ和τ′分别为土石混合体名义剪应力和有效剪应力。有效剪应力τ′与剪切相对位移u可认为服从线弹性变形关系，即：

τ′=ksu

(8)

式中：ks为土石混合体剪切刚度。

将式(8)代入式(7)可得：

τ=ksu(1-D)

(9)

由式(8)可以看出：当土石混合体完全发生损伤(D=1)时，名义剪应力τ等于0，这显然与试验结果不符，因此需对式(9)进行修正。

事实上，土石混合体抗剪强度由结构力强度和摩阻强度两部分组成。特定法向应力作用下土石混合体在剪切变形初期，剪切微元强度未发生破坏，D等于0，宏观剪切过程表现为线弹性变形，但是，当剪应力不断增大至剪切屈服应力时，土石混合体剪切微元强度开始发生破坏，D由0递增，结构力强度逐渐破坏，初始裂隙萌生并不断扩展为局部贯通的剪切带，这些剪切带局部发生相对滑动，剪切表面形状不规则，随着剪切损伤进一步增大，局部剪切带不断扩展、贯通直至形成宏观剪切面，出现明显的滑动剪切位移，产生滑动摩阻，此时土石混合体抗剪强度主要表现为摩阻强度，D等于1。由此可见，土石混合体抗剪强度成因机制非常复杂，土石混合体处于残余强度变形阶段时摩阻强度可视为剪切残余强度τr。因此，对式(9)进行修正可得土石混合体剪切损伤模型，即:

τ=ksu(1-D)+Dτr

(10)

可以看出，式(10)在考虑剪切变形特征基础上认为土石混合体剪切强度主要来源于结构力强度和摩阻强度，在宏观剪切面形成过程中土石混合体抗剪强度主要表现形式不断发生变化，从微观力学角度合理阐释了土石混合体剪切变形破坏后的残余强度变形特征，尽管该模型与岩石类材料损伤模型形式上一致，但两者力学本质具有明显的差异。

4.3 土石混合体剪切损伤演化模型

根据损伤力学理论可将土石混合体剪切变形破坏全过程视为连续损伤的过程。假定剪切破坏面是由无数抗剪切微元体组成，设在某一级荷载作用下土石混合体损伤变量D为已发生剪切破坏的微元体数Nd与总微元体数N之比，即：

D=Nd/N

(11)

当微元体应力水平S达到抗剪强度F时，微元体发生剪切破坏。假设微元体发生剪切破坏具有随机性，抗剪强度F服从Weibull概率分布，即：

p(S)=(m/F0)·(S/F0)m-1·exp[-(S/F0)m]

(12)

式中：m和F0为分布参数。

于是，任意应力水平区间[S，S+dS]内发生剪切破坏的微元体数目dNd为：

dNd=N·p(S)dS

(13)

当加载F时，发生剪切破坏的微元体数目Nd为：

(14)

于是，结合式(11)～(14)可得：

D=1-exp[-(F/F0)m]

(15)

为了反映微元体强度受到应力状态和损伤阈值的影响，根据土石混合体剪切强度特性将微元体强度F的度量方法表示为：

F=τ′-(c+σtanφ)

(16)

于是，将式(8)代入式(16)可得微元体强度F的另一表达方法，即：

F=ksu-(c+σtanφ)

(17)

随着发生剪切破坏的微元体数量不断增加，D由0递增，直至形成宏观剪切破坏面，D等于1。于是，土石混合体剪切损伤演化模型可表示为：

(18)

可以看出：土石混合体在剪切变形过程中，微元体强度F的度量有3种取值：未发生剪切损伤时，F小于零；恰好发生剪切损伤时，F等于零；发生剪切损伤时，F大于零。因此，土石混合体承受剪应力作用并不意味着发生了剪切损伤，而是当剪应力达到剪切损伤阈值时，微元体发生剪切破坏，土石混合体产生剪切损伤，这显然符合土石混合体剪切强度特性。

4.4 土石混合体剪切损伤本构模型及参数确定

将式(18)代入式(10)，可得土石混合体剪切损伤本构模型为：

(19)

可以看出：要使式(19)能够反映土石混合体剪切变形破坏全过程，还需给出m和F0的确定方法。

由土石混合体剪切试验可知土石混合体剪切变形具有应变软化特性，因此，根据剪切试验曲线在峰值点具有极值特性，建立m和F0的确定方法，即：

(20)

式中：τf和uf分别为剪切试验曲线峰值点处的剪应力和剪切位移。

同时，剪切试验曲线峰值点也须满足式(19)中的第二式，于是，将其与式(20)联立可得m和F0的确定方法分别为：

(21)

(22)

Ff=ksuf-(c+σtanφ)

(23)

由于m和F0的确定方法是基于特定法向应力下剪切试验曲线进行推导建立的，式(21)及(22)含有与法向应力有关的剪应力τf及其剪切位移uf，对于不同的法向应力，τf和uf是不同的，因而m和F0也发生变化。为了建立能够反映不同法向应力下土石混合体剪切变形破坏全过程的剪切损伤本构模型，还需给出不同法向应力下τf和uf的确定方法。

由于土石混合体剪切变形时剪应力达到峰值即认为是强度发生破坏，因而根据土石混合体抗剪强度准则可得：

τf=cf+σtanφf

(24)

式中：cf和φf分别为土石混合体处于峰值剪应力时的结构力和摩阻角。

不同法向应力作用下土石混合体直剪试验表明，峰值点处剪切位移uf与法向应力σ表现为近乎线性关系，即：

uf=ρσ+u0

(25)

式中：ρ和u0为试验参数。

将式(24)和(25)代入式(19)和(20)可得不同法向应力作用下土石混合体剪切损伤本构模型参数的确定方法。至此，该文已获得土石混合体剪切损伤本构模型及其模型参数的确定方法。

4.5 土石混合体剪切损伤本构模型验证

为了验证土石混合体剪切损伤本构模型的可行性与合理性，基于试验方案编号为1#试验曲线进行分析。通过分析不同法向应力下土石混合体剪应力与剪切位移关系曲线可得cf=2.41 kPa和φf=32.19°，试验参数ρ=4.5×10-3mm/kPa，u0=9.33 mm，其余模型参数见表4。

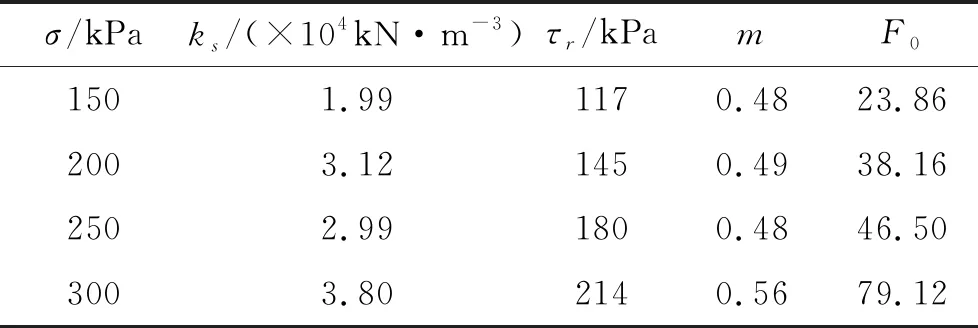
表4 不同法向应力下的模型参数

将上述模型参数代入该文模型可得土石混合体剪应力与剪切位移关系理论曲线，并将其与试验曲线进行比较，如图2所示。

图2 试验与理论曲线的比较

由图2可以看出：

(1) 该文模型不仅能够反映土石混合体剪切过程的阶段性变形特征，即线弹性、应变硬化、应变软化和残余强度等，也能够反映随着法向应力的增大，屈服应力、峰值应力和残余应力及其分别对应的屈服应变、峰值应变和残余应变均会增大的特点。

(2) 不包含非常规力学参数的该文模型能够很好地模拟土石混合体剪切变形破坏全过程，与试验曲线吻合情况良好，验证了该文模型具有一定的可行性和合理性。

5 结论

针对土石混合体剪切强度特性存在的问题与不足，开展对多因素、多水平影响的土石混合体大型直剪试验研究，通过探讨剪切变形特征与机理，引入损伤力学理论，对土石混合体剪切变形破坏全过程模拟方法进行了研究，可得如下结论：

(1) 含石量和含水量是影响土石混合体剪切强度特性的关键因素，含石量增大能够促进土石混合体形成完整土石骨架，含水量过低或过高均对土石混合体剪切强度特性起弱化作用。

(2) 建立了土石混合体抗剪强度准则，其抗剪强度指标表述具有合理性，获得了各因素对结构力和摩阻角的影响规律。

(3) 建立了土石混合体剪切损伤模型和剪切损伤本构模型，给出了模型参数的确定方法，该模型能够很好地反映不同法向应力作用下土石混合体剪切变形破坏全过程，表明该文模型和方法具有一定的合理性与可行性。