多拱肋宽幅异形钢管混凝土拱桥结构参数敏感性分析

李杰， 杜鑫， 张波， 梁岩

( 郑州大学 土木工程学院，河南 郑州 450001)

1 引言

常规拱桥的拱肋为对称曲线，且拱肋位于竖直平面内，平面的支承边界线垂直于拱轴线，不符合上述条件的拱桥均为异形拱桥。多拱肋宽幅异形钢管混凝土拱桥造型优美，不仅满足宽幅桥梁使用需求，而且多个拱肋平面构成不同视觉效果，在城市和有景观要求的地区被越来越多地采用。但由于其造型特殊，特别是结构中柔性可调构件多，受力及变形复杂，相关理论研究不多，相互借鉴性小，导致设计参数对结构静力行为的影响规律不易把握。目前，针对异形拱桥结构力学性能的研究还没有普通拱桥那么广泛，多数研究利用数值方法对关键施工步骤、特殊构件的力学行为进行分析。此外，还有一些研究对合理成桥状态及吊杆张拉、异形拱桥的施工控制等进行了详细分析研究。在这些研究中，有关异形拱桥设计参数对结构力学行为影响的讨论还不多。该文以某多拱肋宽幅异形钢管混凝土拱桥为工程依托，利用ALGOR软件建立精细有限元模型，研究二期恒载、整体升降温、拱肋钢管内填混凝土、拱肋钢管壁厚、索力(包括中吊杆、边吊杆及水平拉索)等单因素设计参数对结构变形、受力的影响；在此基础上，以边拱拱顶应力为例，探讨多拱肋宽幅异形钢管混凝土拱桥多参数对其静力行为的敏感性。

2 工程背景

某多拱肋宽幅异形钢管混凝土拱桥为单跨78 m、全宽59 m的三索面钢管混凝土系杆拱桥。拱肋为3根φ1.5 m钢管组成的空间结构，中拱位于竖直面内，边拱与竖直平面间的夹角为18.925°，中、边拱肋轴线均采用二次抛物线，起拱点间距离均为75 m，中拱肋矢高为25 m、矢跨比为1/3，边拱拱平面内矢高为37 m、矢跨比为1/2.207；拱顶吊杆耳板范围内板厚为40 mm，其余采用36 mm，拱内填C50微膨胀混凝土。拱桥吊杆采用三索面布置，中拱及两边拱分别有11根吊杆，共有PES7-37、PES7-55两种规格，顺桥向吊杆在主梁和拱肋上的锚点间距分别为6、2.5 m，边拱吊杆和中拱吊杆以桥梁纵、横向中线为对称轴，编号由拱顶向拱脚分别记为B0～B5、M0～M5。边拱与中拱间采用刚性斜拉杆连接，斜拉杆分工字形和闭口箱形两种，刚性斜拉杆关于桥梁纵横向中线对称，编号由拱脚向拱顶记为W1～W11。边拱钢管之间通过PES5-37的水平拉索相连，水平拉索以跨中为对称轴，编号由拱脚向拱顶记为T1～T11，各构件的编号及位置详见图1。拱座布置于7 m宽的中央分隔带内。主梁采用纵横梁格体系的钢-混组合梁截面形式，其中钢梁高度为2.75 m(道路标高处)，混凝土桥面板厚度为0.25 m，采用预制结构；根据钢梁截面形式，纵梁分为主纵梁、次纵梁和小纵梁共3种，截面形式有闭口箱形、槽形、工字形3种形式；每侧端横梁下设置6个球形钢支座。图1为大桥的立、平和侧面布置图，该桥结构复杂，造型特殊，设计参数的确定缺少类似桥梁工程参考，可调构件如边拱、中拱吊杆以及水平拉索等对结构的受力和变形等力学行为影响不易把握。

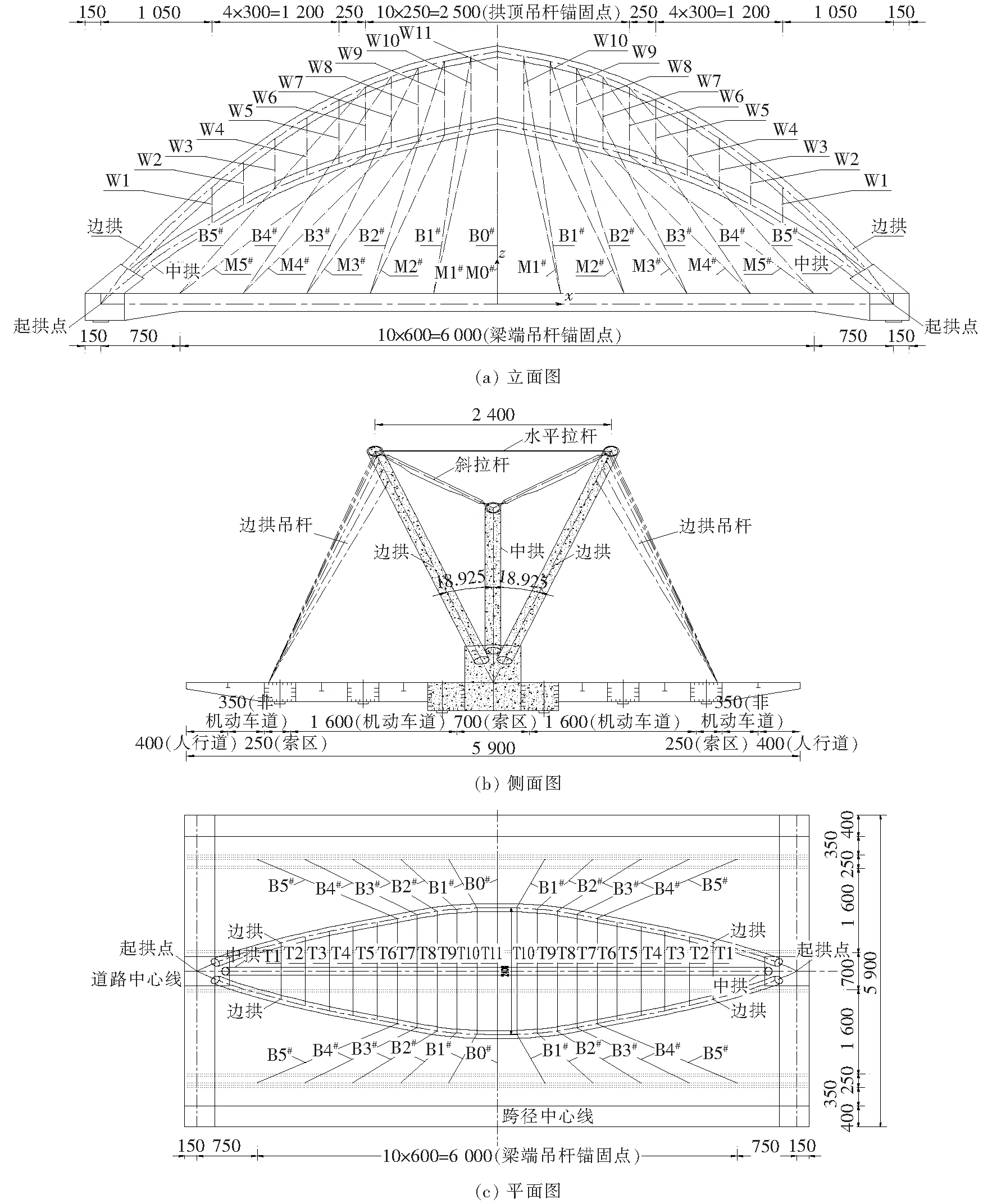
图1 多拱肋宽幅异形钢管混凝土拱桥布置图(单位：cm)

3 有限元模型及分析说明

3.1 有限元模型

采用大型通用有限元软件ALGOR建立大桥整体精细有限元模型，将纵桥向、横桥向和重力负方向记为X、Y、Z轴坐标正方向。其中拱肋和拱脚内填混凝土、预制混凝土桥面板、钢端横梁中的混凝土采用实体单元模拟；钢管拱肋、钢主梁等构件采用板单元模拟；吊杆和水平拉索采用杆单元模拟，斜拉杆采用梁单元模拟。结构自重软件自动计入，二期恒载按照设计图纸计算为面荷载施加于桥面对应位置，吊杆张拉力采用降温方式施加。全桥模型共计136 816个节点，157 096个单元。

3.2 设计参数及分析方法

影响该桥静力力学行为的结构参数可以分为3类：第1类为结构几何参数，如钢管壁厚t、二期铺装集度q(超方或欠方)、钢管中混凝土标号C；第2类为环境参数，主要考虑整体温度T；第3类为索构件张拉力参数，如边拱、中拱吊杆以及水平拉索的主动张拉力Fb、Fz和Fs。

由于该桥对称，为了探讨这些参数对多拱肋宽幅异形钢管混凝土拱桥静力行为的影响，选取边、中拱肋的拱脚、1/4跨和拱顶作为关键截面，分别记为BGJ、BG/4、BGD及ZGJ、ZG/4、ZGD；钢混组合梁选取跨中截面，记为ZHL/2；此外，选择一半的边拱吊杆(B0～B5)、中拱吊杆(M0～M5)和两边拱水平拉索(T1～T11)索力分析参数变化对可调杆件的影响(具体杆件编号见图1)。针对上述参数，以原设计为基准，取参数变化幅度为±10%，进行单因素敏感性分析，通过分析对比归纳这些参数对关键截面的变形、应力以及永存索力的影响。然后，依据单因素分析确定较敏感的参数，考虑多因素交叉影响，探讨多参数对多拱肋宽幅异形钢管混凝土拱桥静力行为的敏感性。

4 单因素敏感性分析

4.1 基准模型分析

鉴于大桥的主要施工过程在支架上完成，且为了探讨设计参数对结构静力行为的敏感性，数值分析没有考虑施工过程，拱肋吊杆和水平拉索按照成桥索力张拉，一次成桥进行分析。限于篇幅，图2仅给出了大桥整体竖向变形、钢构件Von Mises应力、可调构件(吊杆、拉索等杆单元)的永存应力。

由图2可知：大桥钢混主梁的竖向变形最大部位为跨中靠外侧区域，最大下挠-75.6 mm。三拱肋竖向呈现“M”形变形：边拱肋拱顶下挠-43.9 mm，1/4跨上挠15.1 mm；中拱肋拱顶下挠-32.4 mm，1/4跨上挠12.8 mm。由于边拱与竖直平面间夹角为18.925°，因此边拱拱顶横向外倾变形10.3 mm。边拱拱肋钢管拱顶和拱脚Von Mises应力：顶面分别为80.3、114.5 MPa，底面分别为53.5、83.0 MPa。中拱拱肋钢管拱顶和拱脚Von Mises应力：顶面分别为75.5、104.4 MPa，底面分别为49.9、102.1 MPa。永存应力最大的边吊杆和水平拉索均为最长索，其中边拱肋吊杆应力最大为B5(516.5 MPa)，中拱肋吊杆应力最大为M3(511.9 MPa)；拱顶的水平拉索应力最大为T11(605.1 MPa)。分析还表明：拱肋中混凝土的正应力和主应力分布与钢管应力分布有类似规律，即比较拱脚和拱顶截面的混凝土正应力和主应力可以发现，对于拱肋顶、底面应力，均为拱脚部位大于拱顶部位。

4.2 设计参数敏感性分析

4.2.1 结构几何参数

依据前述，几何参数主要考虑钢管壁厚t、二期铺装集度q、钢管中混凝土标号C。分别以原设计为基准，将t、q分别增大和减小10%，混凝土标号取C40、C60，表1为几何参数对结构力学行为的影响结果。

由表1可知：几何参数对结构静力行为有一定影响：① 钢管管壁厚度t变化会引起钢管拱肋的刚度和自重变化，拱肋竖向变形影响最大的位置均为1/4跨截面(边、中拱肋影响相对值为5.3%和6.3%)，边、中拱肋拱顶竖向变形影响相对值分别为3.2%和4.0%；对边拱和中拱的吊杆力、水平拉索索力以及钢主梁的变形、应力影响最大为2.3%(M5)；对钢管应力影响最大为5.8%(中拱肋拱脚顶面)；边拱肋1/4跨截面的横向变形影响最大为6.3%；且影响相对大的工况均为钢管壁厚减薄；② 二期恒载q变化会引起桥梁结构整体恒载变化，拱肋变形影响最大的位置均为1/4跨截面，边、中拱肋影响相对值为2.7%和2.3%，边、中拱肋拱顶变形影响相对值分别为2.1%和1.5%；对边拱B3吊杆力影响相对值为2.4%、对中拱M0吊杆力影响相对值为3.3%，水平拉索索力影响相对值为1.0%(T10)，对钢主梁的变形影响相对值为4.5%、应力影响最大变化为3.7%；对钢管应力影响最大为3.5%(边拱肋拱脚底面)；边拱肋拱顶截面的横向变形影响最大为7.8%；③ 混凝土标号C由C50变化为C40、C60，引起混凝土弹性模量变化为-0.3%、6.9%，拱肋竖向变形影响最大的位置均为1/4跨截面(边、中拱肋影响相对值为2.7%和3.9%)，边、中拱肋拱顶竖向变形影响相对值分别为2.3%和3.1%；对边拱和中拱的吊杆力、水平拉索索力以及钢主梁的变形、应力影响最大变化为1.0%；对钢管应力影响最大为3.4%(中拱肋1/4跨底面)；边拱肋横向变形影响最大为1.0%；且影响相对大的工况均为混凝土标号C40。

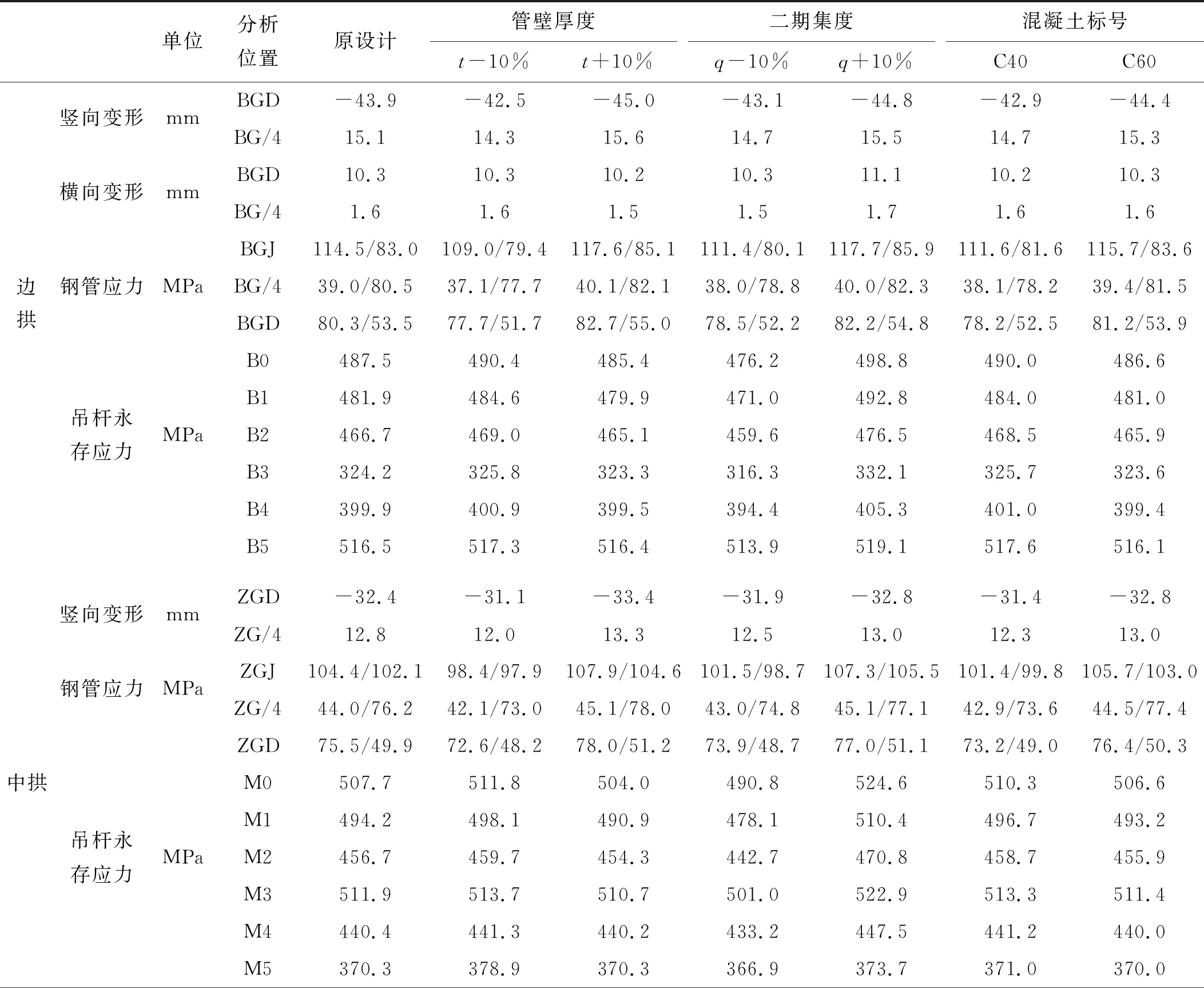
表1 几何参数对结构力学行为的影响

续表1

由上述分析可以看出：几何参数变化对拱肋和钢主梁变形、应力有一定影响，但对吊杆和水平拉索的影响较小，且几何参数变小对结构静力行为的影响相对显著。

4.2.2 环境参数

环境参数考虑了结构所有构件的整体升降温影响，图3～5为温度参数T对结构力学行为的影响结果。

图3 整体升降温对拱肋变形的影响

由图3～5可以看出：环境参数整体升降温T对边、中拱拱顶竖向变形影响较大；对边(中)拱拱顶、拱脚顶面的应力影响较大；整体升降温对水平拉索永存应力影响最大为T3，其余拉索应力影响较小；对中拱吊杆永存应力影响大，其中最大为M2；边拱吊杆永存应力影响最大为B3。由此可以看出：整体升降温T是影响结构静力行为的重要参数。

(a) 钢管拱肋顶面应力

(b) 钢管拱肋底面应力 图4 整体升降温对钢管拱肋应力的影响

(a) 拱肋吊杆永存应力

(b) 水平拉索永存应力 图5 整体升降温对永存应力影响

4.2.3 索构件张拉力参数

索构件张拉力参数主要指边拱、中拱吊杆以及水平拉索中主动张拉力。分析中分别按照边拱、中拱吊杆和水平拉索索力整体变化分析张拉力参数的影响。限于篇幅，图6仅给出部分结果。

图6 索构件张拉力对结构静力行为的影响

图6表明：中拱吊杆和水平拉索的张拉力对钢管和钢主梁应力影响很小；边拱、中拱吊杆以及水平拉索的张拉力对拱肋竖向变形影响小，但对边拱横向变形影响较显著；此外，边拱吊杆对中拱吊杆和水平拉索的永存应力影响大。因此，对水平拉索和中拱吊杆永存应力影响显著的参数为边拱吊杆张拉力，水平拉索和中拱吊杆张拉力对边拱吊杆永存应力影响很小，对拱肋横向变形敏感的参数为边拱吊杆、中拱吊杆和水平拉索的张拉力。

4.3 多参数敏感性分析

对于复杂的桥梁结构，力学行为规律复杂，仅通过单参数分析很难说明参数之间的交叉影响。为了探讨多参数对结构某力学响应的敏感性，可以应用Design-Expert软件进行多参数的回归分析。限于篇幅，以边拱拱顶的顶面应力σBGD为例进行多参数敏感性分析。由前面分析可知σBGD对t、q、C、T和Fb较敏感。5个参数生成的试验设计数据如表2所示，表2中参数水平值1(-1)分别代表参数的高水平(低水平)取值，1.82(-1.82)为软件生成的参数水平放大系数，0表示原设计值，经过多参数组合后得到σBGD。

表2 多参数试验设计

由表2可得：整体升降温T对σBGD影响最显著，其次是钢管壁厚t和整体升降温T、钢管壁厚t和边拱吊杆力Fb、二期铺装q和整体升降温T、混凝土标号C和整体升降温T、整体升降温T和边拱吊杆力Fb的交叉影响，此外整体升降温T的平方项对σBGD也有一定影响。回归后的关系式如式(1)所示。那么，在正常施工运营条件和环境条件下，且结构材料未超出线弹性范围，该公式可不依赖有限元数值分析，仅通过参数取值即可得出响应值。

(1)

式中：σBGD为边拱拱顶Von Mises应力(MPa)；t为钢管壁厚(mm)；q为二期铺装集度(N/mm2)；C为钢管中混凝土标号；T为整体升降温(℃)；Fb为边拱吊杆张拉力(N)。

5 结论

多拱肋宽幅异形钢管混凝土拱桥的结构参数可分为几何参数、环境参数和索构件张拉力参数3类，该文分析了单参数对结构静力行为的敏感性，并对多参数交叉影响进行探讨。主要结论如下：

(1) 一次成桥分析显示多拱肋宽幅异形钢管混凝土拱桥的各拱肋竖向呈现“M”形变形，永存应力最大的边吊杆和水平拉索均为最长索，中拱肋吊杆最大永存应力为1/4跨吊杆。

(2) 几何参数变化对拱肋和钢主梁变形、应力有一定影响，但对吊杆和水平拉索的影响较小，且几何参数变小对结构静力行为的影响相对显著。

(3) 整体升降温对边、中拱拱顶竖向变形和边(中)拱拱顶、拱脚顶面的应力影响较大，对1/4跨附近的水平拉索、中拱吊杆和边拱吊杆永存应力影响大；边拱吊杆张拉力对水平拉索和中拱吊杆永存应力影响显著，对拱肋横向变形敏感的参数为边拱、中拱和水平拉索张拉力。

(4) 边拱拱顶的顶面应力多参数敏感性分析显示：整体升降温对应力影响最显著，且应考虑不同参数交叉影响；通过试验设计可得到多因素交叉影响的响应计算公式，且该公式不必再进行有限元数值分析就能得到响应值。