悬挂式单轨交通系统连续轨道梁桥静力分析与截面参数比较研究

邱靖权,郑凯锋,熊籽跞

(西南交通大学土木工程学院,成都 610031)

引言

随着我国经济的迅猛发展以及城市化水平的不断提高，城市拥堵以及汽车排放污染等问题逐渐凸显，而城市轨道交通的出现，有效地缓解了这些问题。悬挂式单轨交通系统作为新型城市轨道交通，起步虽然晚于地铁和跨座式轨道交通，但凭借其地形适应能力强，能耗低、运输量适中和环境友好型[1-3]等一系列优点，在中等城市中具有广阔的发展前景[4-6]。目前，我国多座城市已开始规划和布局相应交通线路。

与传统的轨道梁不同，悬挂式单轨系统桥梁的轨道梁是实现其跨越能力的关键构件，轨道梁截面形式为下部开口箱梁，呈Π形。编组列车的走行轮及转向轮均在梁内，走行轮行走于底板上，列车的转向依靠腹板及与其接触的转向轮实现，因此轨道梁的设计、制造以及安装的精度均有非常严格的要求[7]；同时线路的电缆、管道等也均放置于轨道梁内，降低了相应养护维修成本[8-9]。

目前，德国与日本的悬挂式单轨系统技术已经相当成熟，并且已经应用于多条轨道线路[10-14]。而国内引进悬挂式轨道交通系统时间较短，缺乏系统性研究以及设计经验，并且尚未统一设计标准，故目前已有的设计方案均相对保守[15-18]。为保证悬挂式单轨交通系统设计的经济性与合理性，并为我国相关设计人员提供参考，结合一座悬挂式连续钢轨道梁桥设计，分析计算其在各个荷载组合下的应力与变形，研究各截面参数对结构强度、刚度以及用钢量的影响，最后以用钢量最少为目标进行适当参数削减，提出新方案，并建立新方案下的有限元模型进行强度和刚度检算。

1 方案设计

本文分析采用的悬挂式单轨交通系统连续轨道梁桥为(40+60+40) m钢结构轨道梁，两线轨道梁之间采用钢横梁连接，全桥钢梁采用Q345qD，总体布置如图1所示。

图1 总体布置(单位：mm)

悬挂式轨道梁桥的桥墩形式主要分为单线的倒L形和双线的门形、T形以及球拍形桥墩[19]。本桥的桥墩为门形墩，如图2所示，与传统门形墩不同，悬挂式单轨系统轨道梁并不是放置在门形墩的盖梁顶部，而是从盖梁下伸出两块吊梁，吊梁水平伸出牛角以放置支座并承受轨道梁传递的荷载。

图2 门形墩构造形式

轨道梁采用Π形截面，且为变截面，截面在中跨梁高最大且为2.5 m，在边跨靠近支座处梁高最小且为1.5 m，轨道梁截面形式如图3所示。此外，支座处的轨道梁顶板宽为1.372 m，在其余处顶板宽为1.172 m；顶板厚度为36 mm，顶板加劲肋厚度为30 mm，沿纵向每1 m布置1道顶板加劲肋，在支座处加密。腹板厚度为36 mm，腹板加劲肋厚度为30 mm，沿纵向每1 m布置1道腹板加劲肋，并在支座处加密。局部加劲底板的最薄处厚度为32 mm，底板加劲肋厚度为30 mm，沿纵向每1 m布置1道底板加劲肋，并在支座处进行加密。两线轨道梁之间除支座处不布置横梁外，其余位置每隔5 m设置1道横梁。

图3 轨道梁截面形式(单位：mm)

2 连续轨道梁桥静力分析

2.1 有限元模型

运用MIDAS/CIVIL建立全桥梁单元模型，双线钢轨道梁分开建模。轨道梁的每段梁单元长度为1 m并在支座处加密，每片横梁分为3段；桥梁的支座为球形钢支座，采用弹性连接模拟钢轨道梁与桥墩之间的连接，并且由于横向支座中心间距小于4 m，故将每个支座都进行横向约束；桥墩盖梁在横桥向均匀分段，并在吊板处适当加密；墩底采用固结约束。全桥模型共有659个节点，609个单元，全桥空间梁单元模型整体结构如图4所示。

图4 全桥梁单元模型

2.2 荷载类型及其组合

由于国内暂无悬挂式单轨系统的统一规范，本文依照专门编写的《四川省悬挂式单轨设计规范》中条文提出的要求在静力计算中考虑以下荷载：(1)结构自重与附属设备及附属建筑自重；(2)列车竖向静活载；(3)列车竖向动力作用；(4)列车横向摇摆力；(5)列车制动力；(6)风力；(7)温度影响力。

根据规范要求，列车竖向静活载采用最大轴重为4.5 t的两辆编组列车，每辆编组列车各有6对车轴，4个重轴轴重4.5 t，中间两个轻轴轴重0.75 t；两辆编组列车之间的轴距为2.1 m，相邻重轴间距为1.6 m，相邻轻轴间距为3.6 m，重轴与轻轴间距为0.95 m，列车各轴重布置如图5所示。

图5 列车静活载轴重布置(单位：m)

根据不同荷载组合，将材料基本容许应力和地基容许承载力乘以不同的提高系数，提高系数按表1选取，以此计算分析桥梁运营阶段下各最不利工况的内力、应力及变形。

表1 荷载组合及容许应力提高系数

2.3 计算分析

计算得到轨道梁主梁在列车竖向静活载作用+0.5倍温度影响力下产生的最大挠度值为23.72 mm，小于《四川省悬挂式单轨设计规范》规定的限值66.00 mm，如图6所示；而列车静活载作用下轨道梁桥由于挠度产生的梁端转角为1.73‰，小于规范规定的3.00‰，如图7所示。各个荷载组合作用下的应力计算汇总如表2所示。

图6 列车竖向静活载+0.5倍温度作用下的挠度(单位：mm)

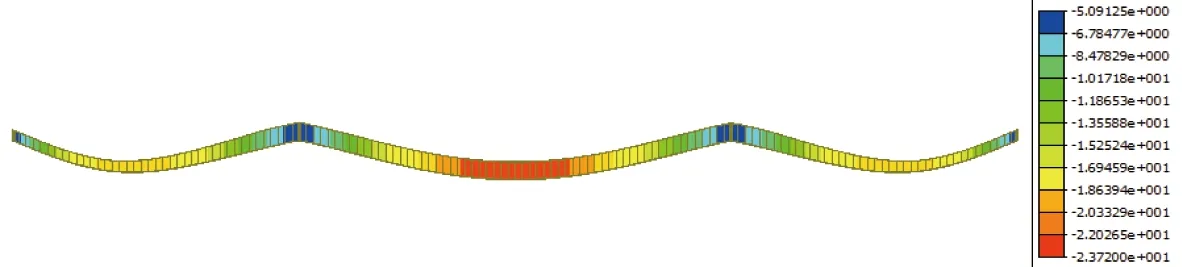
图7 列车静活载作用下的梁端转角(单位：rad)

计算结果表明，在组合3(恒载+列车活载+列车横向摇摆力+整体降温)作用下，钢主梁上缘产生最大组合应力80.0 MPa，并在下缘产生最小组合应力-81.0 MPa；而在组合6(恒载+列车活载+列车横向摇摆力+有车风荷载+整体升温)作用下，钢主梁上缘产生最小组合应力-55.0 MPa，并在下缘产生最大应力58.6 MPa；并且在组合7作用下，横梁产生最大组合应力和最小组合应力，其中最大组合应力为37.0 MPa，最小组合应力为-28.7 MPa。轨道梁各个部件在各个荷载组合下的组合应力极值均远小于相关设计规范条文所规定限值要求。

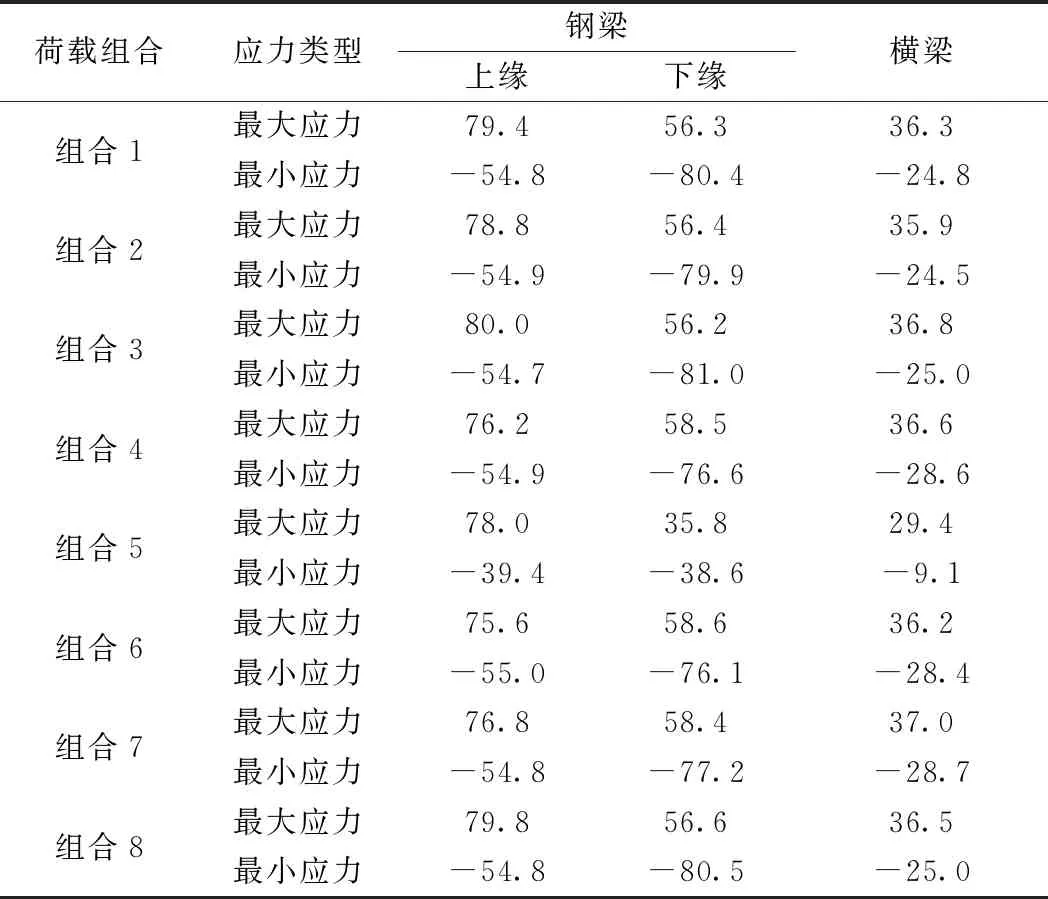
表2 轨道梁应力计算汇总 MPa

3 轨道梁截面参数比较分析

根据计算分析，本桥在各个荷载组合下的顶板、底板和腹板的最大应力以及变形等均远小于规范限值，钢材性能并未得到充分利用，不仅增加了工厂制造成本，也增加了现场施工的难度[20]。基于以上原因，利用MIDAS/CIVIL软件分别对轨道梁变截面高度、顶板厚度、腹板厚度和底板厚度等进行参数影响分析。根据参数分析结果进行适当的参数削减，以达到减少用钢量，降低成本，使设计更为合理的目的。

由各荷载组合下结构应力计算结果可知，各荷载组合下的轨道梁最大和最小组合应力差异并不大。取最不利的荷载组合3(恒载+列车静荷载+列车动力作用+列车横向力+整体降温)对不同参数条件下的结构应力和变形进行对比分析，各截面参数如图8所示。

图8 截面参数

3.1 变截面高度影响分析

梁高是影响桥梁刚度的重要因素之一，轨道梁的高度越高，则其刚度越大，但与此同时其自身的重力也会相应增加，因此梁高越高并不一定越有利于受力和变形。本桥边跨支点处截面高1.5 m，中跨支点处截面高为2.5 m，在满足轨道梁刚度和强度以及其他参数不变的条件下，分别取中支点处截面高度H为2.3，2.1，1.9，1.7 m和1.5 m，采用中跨等截面边跨变截面设计，其中H=1.5 m时为等截面设计。

对以上几组参数分别建立有限元模型进行分析，并与原方案结果(最大梁高为2.5 m)进行对比，计算得到各最大梁高下的轨道梁应力、竖向挠度以及梁端转角如表3所示。

表3 不同最大梁高下的轨道梁应力与变形

3.2 顶板厚度影响分析

顶板厚度对于结构的强度与刚度也有一定的影响，在满足轨道梁刚度和强度以及其他参数不变的条件下，逐渐减小顶板厚度以分析其对结构受力与变形的影响。分别取顶板厚度T为32，28，24，20 mm和16 mm分别建立有限元模型进行分析，并与原结果(顶板厚度为36 mm)进行对比。计算得到各顶板厚度下的轨道梁应力、竖向挠度以及梁端转角如表4所示。

表4 不同顶板厚度下的轨道梁应力与变形

3.3 腹板厚度影响分析

在满足轨道梁刚度和强度以及其他参数不变的条件下，逐渐减小腹板厚度以分析其对结构受力与变形的影响。分别取腹板厚度F为32，28，24，20 mm和16 mm分别建立有限元模型进行分析，并与原结果(腹板厚度为36 mm)进行对比。计算得到各腹板厚度下的轨道梁应力、竖向挠度以及梁端转角如表5所示。

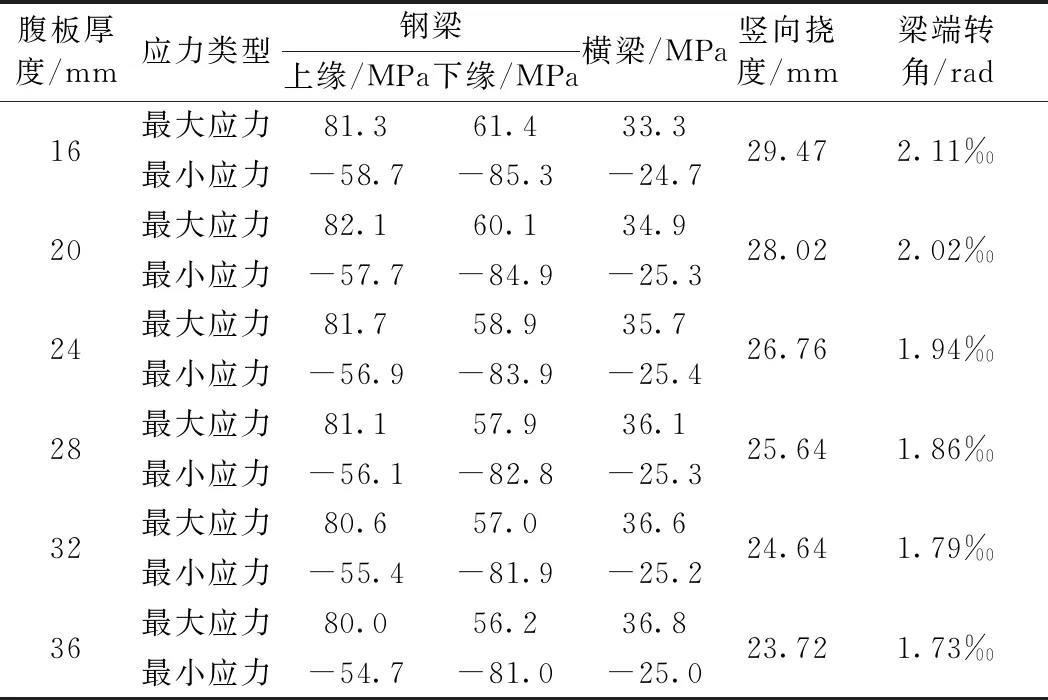
表5 不同腹板厚度下的轨道梁应力与变形

3.4 底板厚度影响分析

在满足轨道梁刚度和强度以及其他参数不变的条件下，逐渐减小底板厚度B以分析其对结构受力与变形的影响。由于底板内侧最薄处只有20 mm，故只能分别取底板外侧最厚处厚度B为28，24 mm和20 mm分别建立有限元模型进行分析，并与原结果(底板最厚处厚度为32 mm)进行对比。计算得到各底板厚度下的轨道梁应力、竖向挠度以及梁端转角如表6所示。

3.5 轨道梁截面参数比较分析

梁高为1.5 m的轨道梁总长30 m，变截面轨道梁总长40 m，最大梁高H的轨道梁总长70 m，因此可得到顶板、腹板、底板所用钢材体积V1(m3)、V2(m3)和V3(m3)分别为

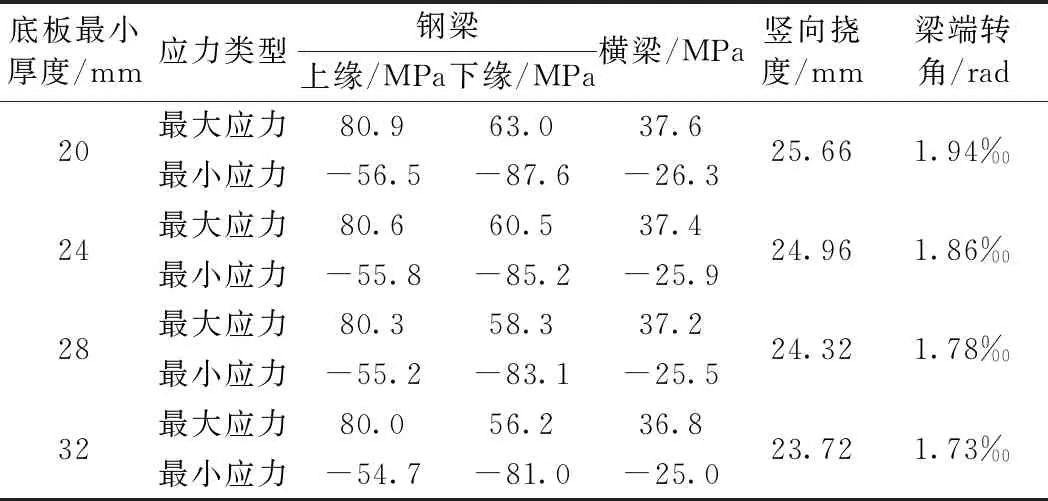
表6 不同底板厚度下的轨道梁应力与变形

V1=

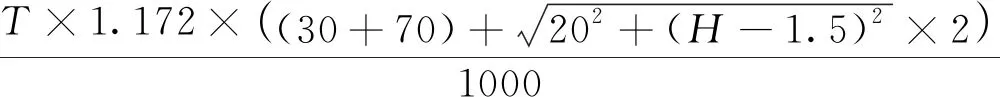
(1)

V2=

0.09HF+0.075F

(2)

(3)

轨道梁的总用钢体积V=V1+V2+V3，当顶板厚T在16～40 mm，腹板厚F在16～36 mm，底板厚B在20～32 mm，最大梁高H在1.5～2.5 m范围内时，将式(1)到式(3)相加得到总用钢体积V(m3)后，分别对T、H、F、B求偏微分，可以得到各偏微分值的范围如表7所示。

表7 总用钢体积V对各截面参数偏微分值范围

由表7可以得到，对于总用钢体积(总用钢量)而言，各参数影响程度从大到小依次是最大梁高H，腹板厚度F，顶板厚度T，底板厚度B。

综合轨道梁变截面高度、顶板厚度、腹板厚度和底板厚度对其竖向挠度、梁端转角与应力的影响，可以看出：(1) 对于竖向挠度，影响程度从大到小依次是最大梁高H，腹板厚度F，顶板厚度T，底板厚度B；(2) 对于梁端转角，影响程度从大到小依次是最大梁高H，顶板厚度T，底板厚度B，腹板厚度F；(3) 对于钢梁最大应力，影响程度从大到小依次是最大梁高H，顶板厚度T，腹板厚度F，底板厚度B；(4) 对于钢梁最小应力，影响程度从大到小依次是最大梁高H，底板厚度B，腹板厚度F，顶板厚度T。因此，各项轨道梁截面参数对钢梁应力、变形以及用钢量的影响如表8所示。

表8 各截面参数对轨道梁应力、变形及用钢量影响程度

由于各条件下的钢梁应力均远小于规范规定的容许应力，因此以竖向挠度和梁端转角满足规范要求为条件，以用钢量最小为目标，提出截面材料最省方案，最后再建模对强度进行检验。

根据得出的各截面参数与竖向挠度和梁端转角的关系，可以推出保持最大梁高H为最小值1.5 m，腹板厚度F与底板厚度B保持最初设计值不变，适当增加顶板厚度T，可在满足刚度要求的情况下，达到用钢量最小的目的。最终得到在用钢量最省的情况下的各截面参数值分别为：最大梁高H为1.5 m，腹板厚度F为36 mm，底板最厚处厚度B为32 mm，顶板厚度T为40 mm。建立梁单元模型，进行分析计算之后得到钢梁应力、变形以及与原设计结果的对比如表9所示。

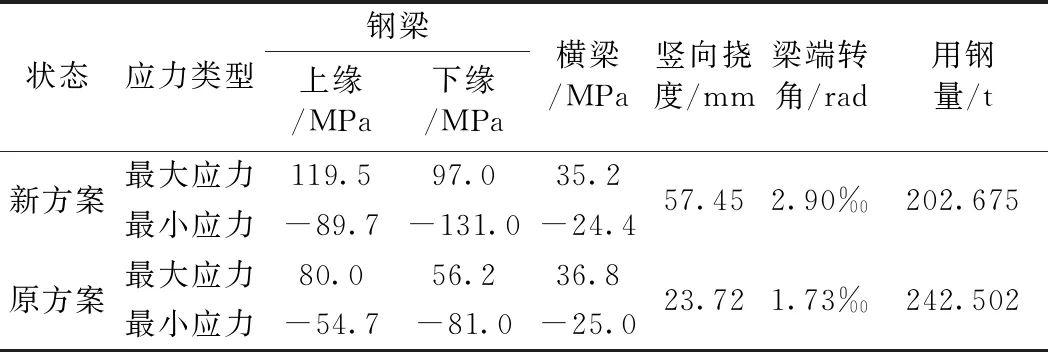
表9 新旧方案轨道梁应力与变形对比

根据表9可知，在保证轨道梁刚度的情况下，以减小用钢量为目标得到的新方案下轨道梁强度依然满足要求，并且用钢量减少16.4%，约39.827 t；同时，变截面连续轨道梁变为了等截面连续轨道梁，也减少了工厂加工成本以及现场施工难度。

4 结论

结合(40+60+40) m悬挂式连续钢轨道梁桥设计，通过MIDAS/CIVIL软件建立全桥梁单元模型，计算各荷载组合下结构的应力与变形，并分析各截面参数对结构应力、变形以及用钢量的影响，最后以用钢量最省为目标提出新方案，并进行强度、刚度验算，得到结论如下。

(1) 原设计方案在最不利荷载组合作用下的变形与应力均满足规范要求，且变形与应力幅值均远未达到规范容许限值。

(2) 提出的新方案结构强度与刚度均满足规范要求，并且用钢量较原设计方案减少了16.4%，约38.827 t；同时变截面连续梁变为等截面连续梁，降低了工程成本及现场施工难度。