地震作用下悬挂式单轨车桥系统动力性能分析

徐 翔,蔡成标,何庆烈,朱胜阳,杨泽钰

(西南交通大学牵引动力国家重点实验室,成都 610031)

1 概述

随着我国城镇化进程的不断推进和城市建设的飞速发展，城市地面交通拥堵问题愈加严重，大力发展能源消耗低、运输能力强和快捷安全的轨道交通刻不容缓。相比传统的地铁、轻轨等轨道交通形式，悬挂式单轨作为一种新型的中低运量的轨道交通系统，具有施工简便、占地少、投资小、工期短、噪声低、适应性强、乘坐舒适、视野开阔等诸多优点[1-2]。除此之外，悬挂式单轨交通可与常规公交、轨道交通等其他公交方式错位发展，是其他公共交通方式的有益补充和完善。图1为成都双流悬挂式单轨试验线。

图1 悬挂式单轨试验线

悬挂式单轨系统的轨道梁由钢立柱或水泥立柱支撑在空中，车体悬挂于轨道梁下方[3]。在正常运行情况下，轨道梁主要的振动来源为车辆、轨道梁与桥梁间相互作用所产生的振动[4]，轨道梁结构处于其承载范围内。但是当地震发生时，由于地震导致的轨道梁桥结构振动与列车动力作用相互叠加，悬挂式单轨系统将产生强烈的振动，甚至造成破坏，影响桥上运行列车的安全性和平稳性，对人民的生命财产造成巨大的威胁[5]。

我国早期关于悬挂式单轨交通的研究主要集中在悬挂式单轨的适用性研究。2010年以来，相关研究人员才逐渐开展了悬挂式单轨车辆及轨道结构的动力学计算研究。胡晓玲[6]建立悬挂式单轨车辆整车动力学仿真模型，并分析车辆通过曲线时，行车速度、曲线半径和车体质心位置等因素对车辆动力性能的影响；李天一[7]通过分析一系悬挂参数对车辆动力学性能影响，对其进行分析和优化，并提出了合适的数值；鲍玉龙[8]运用Simpack和ANSYS实现了悬挂式单轨交通系统车桥耦合振动的联合仿真分析，并分析了列车运行速度，轨道不平顺以及列车编组等因素对轨道梁和车体的动力响应影响；He[9-10]针对我国第一条悬挂式单轨交通试验线开展行车动力学试验，并根据试验线建立悬挂式单轨交通的车桥耦合系统，对悬挂式单轨交通系统轨道梁进行分析。

同时，目前也有许多学者研究了地震对铁路动力影响。韩艳[11]等采用相对运动法建立长大跨度桥梁—列车耦合系统的地震反应分析模型，讨论了列车速度和地震波行波效应对车桥系统动力响应的影响；ZHANG[12]等采用大质量法建立铁路斜拉桥车-桥-地震耦合系统模型，讨论了车桥响应与地震波速之间变化关系；彭立顺[13]对地震作用下高速列车通过桥梁时系统的动力响应进行了数值计算；徐鹏[14]通过建立地震作用下列车-轨道-路基耦合动力学模型，分析了地震强度和行车速度对结构响应的影响规律，并得到列车运行安全域；雷虎军[15]等分析了高速列车在不同地震激励输入方式下车辆和桥梁的动力响应区别；杨尚福[16]利用动力学分析软件TTBSIM，分析了地面振动对于高速铁路桥梁和行车的影响。

但到目前为止，针对地震作用下悬挂式单轨车辆-轨道梁桥耦合振动分析的研究还是空白。本文运用车辆-轨道耦合动力学理论[17]，建立地震作用下悬挂式单轨车辆-轨道梁桥耦合动力学振动模型，探究地震作用下悬挂式单轨系统的动力响应，对悬挂式单轨系统抗震设计具有一定的参考意义。

2 地震作用下悬挂式单轨车桥动力分析模型

地震作用下悬挂式单轨车辆-轨道梁桥系统振动分析模型是由车辆系统和轨道梁桥系统组成，通过轮轨关系耦合，地震荷载作为外部激励作用在该系统上[18]。图2为地震作用下悬挂式单轨车辆-轨道梁桥动态相互作用原理。

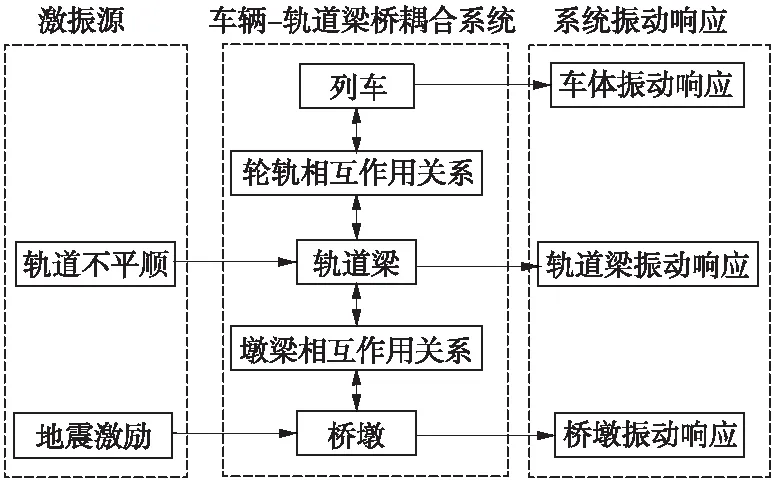
图2 地震作用下悬挂式单轨相互作用原理

2.1 悬挂式单轨车辆模型

悬挂式单轨车辆系统各部件从上到下主要由摇枕、构架、中心销、吊梁以及车体组成，其中摇枕是通过二系悬挂装置连接在构架上，中心销通过旋转铰和摇枕进行铰接，中心销和车体间通过四连杆机构连接，该四连杆机构能释放一定的车体横向约束，从而起到减少列车横向冲击作用。此外，四连杆机构内部还具有抗横摆减振器和两个弹性止挡，可对车体起到良好的横向减振与横向限位作用。该动力学分析模型各部件连接方式与悬挂式单轨系统实际结构相同。

据此，将每节车辆离散为1个车体、2个构架和2个由摇枕和中心销共同组成的吊臂，共5个多刚体系统来研究其力学行为，将车体和每个转向架各考虑沉浮、横移、侧滚、摇头、点头5个自由度，每个吊臂考虑沉浮、横移和侧滚3个自由度，共21个自由度，将各轮胎简化为弹簧阻尼原件。在实际结构中，中心销与摇枕间只有一个绕垂向的旋转自由度，而其他自由度方向与摇枕均为刚性连接。为了简化模型且同时保证模型的准确性，在沉浮、横移、侧滚运动中，可将摇枕和中心销视为一个吊臂刚体来研究其力学行为[19]。车辆动力学模型见图3、图4。

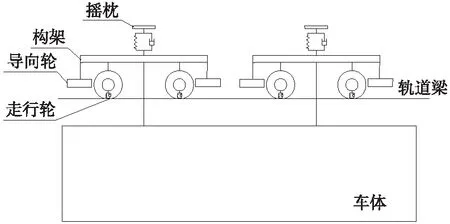
图3 车辆动力学模型正视

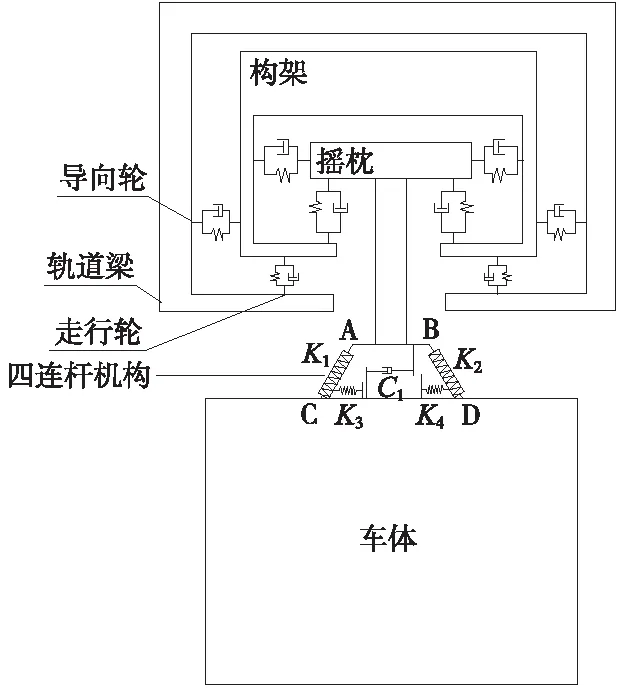
图4 车辆动力学模型侧视

2.2 悬挂式单轨轨道梁桥模型

悬挂式单轨轨道梁为下部分开口钢结构箱梁，沿纵向布置有加强筋来提高轨道梁的刚度，箱梁与桥墩间采用销轴连接方式。应用有限元软件ANSYS，建立了跨长为25 m的精细轨道梁三维有限元模型，包含轨道梁体和桥墩。鉴于轨道梁各部分为钢板焊接而成，模型中采用SHELL181板单元，同时利用有限元软件中节点耦合功能来实现梁体与桥墩间的简支约束，如图5、图6所示。

图5 轨道梁桥ANSYS有限元模型

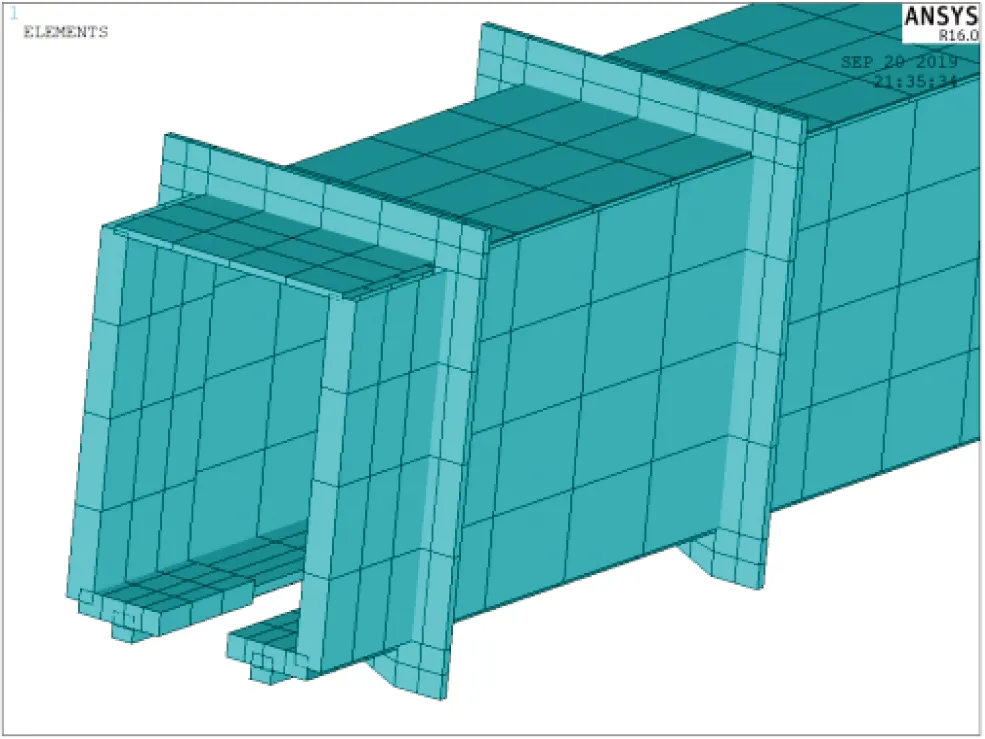
图6 轨道梁端部有限元模型

2.3 地震波施加方法

图7为地震作用下悬挂式单轨车辆-轨道梁耦合振动模型，模型可划分为结构支承部分和结构非支承部分。地震发生时，地震波作用于结构支承部分，通过使结构支承部分的位移、速度及加速度满足地震动边界条件，从而作用于整个耦合振动模型，影响车辆-轨道梁整个系统。

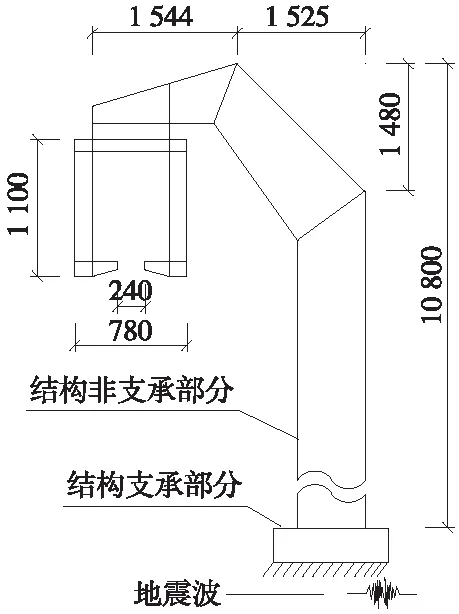
图7 地震作用下悬挂式单轨动力分析模型(单位：mm)

在地震响应分析中，主要的地震波输入方法有直接求解法、拟静力位移法和大质量法[20-21]。对于悬挂式单轨车辆-轨道梁动力相互作用模型，由于地震波要通过非线性轮轨接触关系作用于车辆结构，且大质量法可以考虑行波效应，实现结构的多点地震波输入，方便地在通用有限元程序中实现，因此本文采用大质量法对结构施加地震波。

大质量法的原理是通过质量矩阵中结构支承部分的质量元素乘大数，使得结构支承部分的位移、速度及加速度满足地震波边界条件。在ANSYS中采用大质量法处理地震波边界条件的做法是：首先在结构支承部分节点定义大质量块a(a一般为结构总质量的106～108倍)，并释放结构支承部分节点地震波输入方向的约束，然后对结构支承部分施加动力时程，从而带动整个结构振动。根据其原理，轨道梁桥系统的运动方程可变为

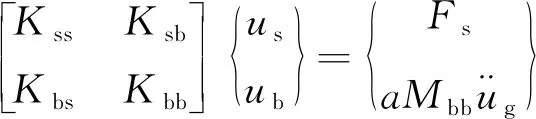
(1)

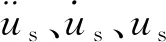
化简可得

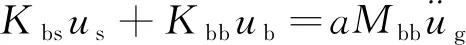
(2)

由于a为结构质量的106～108倍，远远大于其他项，因此近似得到

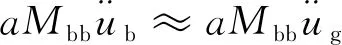
(3)

从而可得

(4)

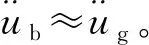
2.4 模型验证

应用悬挂式单轨车辆-桥梁系统振动分析模型，在不考虑地震作用下，车辆运行速度为30 km/h，仿真结果与现场试验测试结果[19]对比，如表1所示。

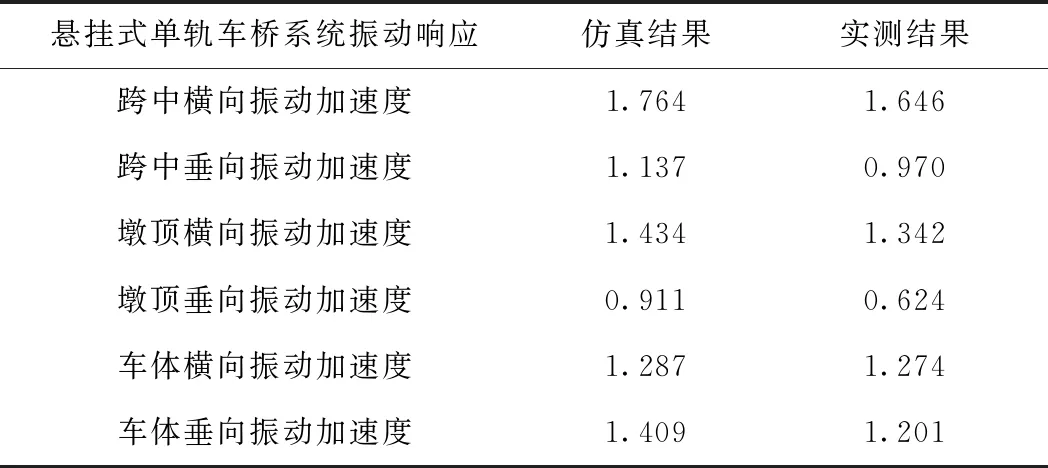
表1 无地震作用时仿真结果与实测结果对比 m/s2

由表1可见，通过大质量法建立的地震荷载作用下悬挂式单轨车辆-桥梁系统振动分析模型计算结果与现场试验测试结果吻合较好，验证了该有限元模型的可靠性。

3 地震作用下悬挂式单轨车桥动力性能分析

3.1 计算条件

以成都双流中唐悬挂式单轨试验线为研究对象，悬挂式单轨车辆参数如表2所示。

表2 悬挂式单轨车辆运行工况参数

根据《中国地震动区划图》，成都双流地区抗震设防烈度7级，Ⅱ类场地类型，设计基本加速度0.1g。参考我国《建筑抗震设计规范》和《建筑工程抗震性态设计通则》附录F中推荐的地震动记录中的规定，选择在结构设计中广泛应用、具有代表意义的El Centro地震波作为输入地震波，其基本特性及加速度时程曲线如表3和图8所示。

表3 输入地震波参数

图8 El centro地震动加速度时程记录

《建筑抗震设计规范》规定，当结构采用三维空间模型需要双向地震波输入时，其加速度最大值通常按最不利条件考虑，地震波横向和垂向的比例按照1∶0.65进行规范化处理。因此，将El Centro地震波进行规范化处理后沿悬挂式单轨横向和垂向同时输入。由于悬挂式单轨跨度较小，因此不考虑地震波的行波效应和多点激励的影响。计算中假设列车在轨道梁上运行时地震发生，轨道不平顺选用悬挂式单轨试验线实测轨道不平顺。

3.2 结果分析

3.2.1 典型工况的动力响应时程曲线

列车运行速度为30 km/h，地震动强度为0.1g为例，El centro地震波作用下车体振动加速度、轨道梁跨中振动加速度以及桥墩墩顶振动加速度的时程曲线如图9、图10所示。

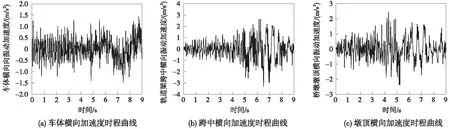
图9 El Centro地震波作用下车辆-轨道梁桥横向振动响应时程曲线

图10 El Centro地震波作用下车辆-轨道梁桥垂向振动响应时程曲线

通过对比图8和图9、图10可发现，由于El Centro横向地震波加速度在5 s时急剧增加且波动变化较大，因此车体、轨道梁跨中及桥墩墩顶的横向加速度均在5 s后出现明显波动。由于悬挂式单轨车-桥系统垂向方面受到轨道不平顺、车辆荷载以及地震波多重激励作用，且经过规范化处理后El Centro垂向地震波强度相对较小，因此车体、轨道梁跨中及桥墩墩顶的垂向加速度相对较为平稳，没有出现较大的波动变化。

3.2.2 地震强度影响分析

为了进一步分析地震强度对于整个悬挂式单轨列车-轨道梁桥系统动力响应的影响，行车速度为30 km/h，将地震波强度按0.05g～0.30g进行规格化处理，计算地震作用下车体和轨道梁的动力响应，各动力响应指标最大值随地震动强度变化规律分别如图11和表4所示。

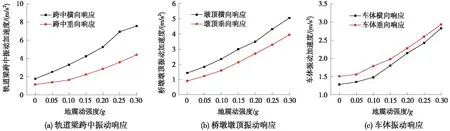
图11 悬挂式单轨车辆-轨道梁桥振动响应随地震动强度变化

表4 不同地震动强度作用下悬挂式单轨车-桥系统响应最大值

由图11可以看出：随着地震动强度的增大，悬挂式单轨车-桥系统各振动响应均近似呈线性规律增加；其中，桥墩墩顶振动加速度受地震波强度影响明显，变化幅度较大；轨道梁跨中横向振动加速度受地震波强度影响变化幅度较大，而轨道梁垂向振动受到轨道不平顺、车辆荷载以及地震波多重激励作用，随地震动强度增加变化幅度较小；由于悬挂式单轨轨道梁结构柔性较大，地震激励通过轨道梁和桥墩的吸收和耗散，传递至车辆时影响相对较小，因此车体垂向和横向振动加速度随地震动强度变化较小。

由表4可以看出，轨道梁跨中横向相对位移变化较大，垂向相对位移变化较小。车体横向侧摆位移在四连杆机构抗横摆减振器和弹性止挡的作用下变化较小，均小于安全限界60 mm，因此不会与桥墩发生碰撞。由于悬挂式单轨车辆走行轮和导向轮始终在箱型轨道梁内运行，因此不会发生脱轨现象。但当地震动强度大于0.2g时，轨道梁跨中垂向相对位移变形大于25 mm，超过其25 m跨度的1/1 000，走行轮轮载变动系数接近0.65，运行垂向平稳性指标接近2.75，车体运行振动强烈，乘客乘坐舒适性较差容易产生恐慌。

3.2.3 行车速度影响分析

将El Centro地震波按照0.1g进行规格化处理，列车运行速度为10～50 km/h，计算地震作用下车体和轨道梁桥的动力响应，各动力响应指标最大值随行车速度变化规律如图12和表5所示。

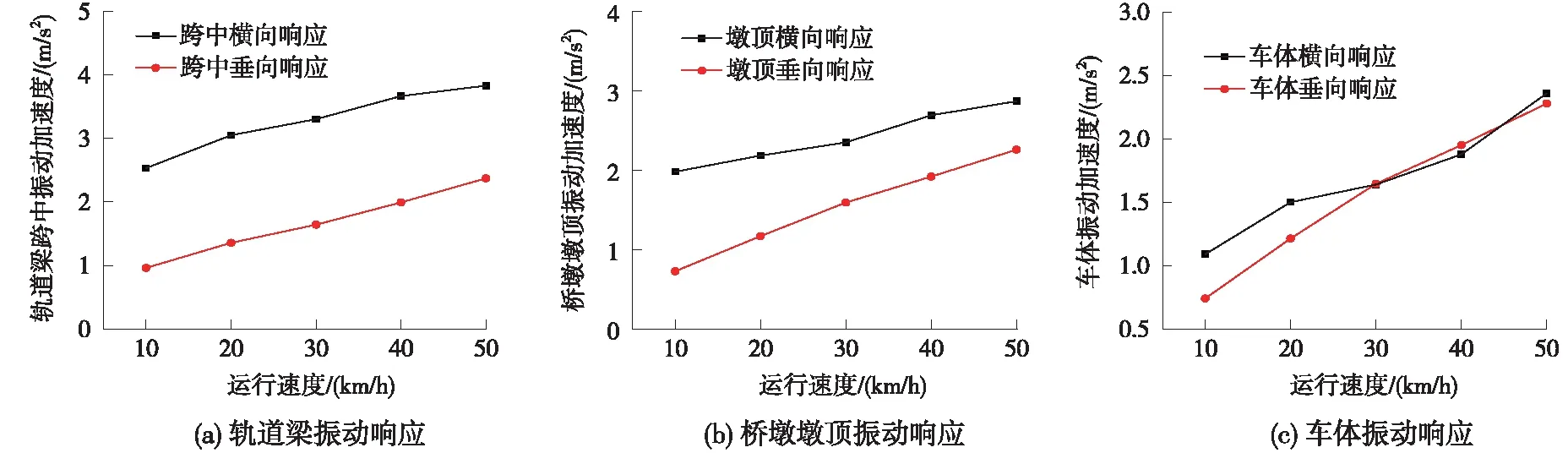
图12 悬挂式单轨车辆-轨道梁桥振动响应随行车速度变化规律

表5 不同行车速度作用下悬挂式单轨车-桥系统响应最大值

由图12可以看出：悬挂式单轨车-桥系统各项振动响应均随行车速度的增加而增大。其中，轨道梁跨中、桥墩墩顶和车体的垂向振动加速度随行车速度的增加大致呈线性规律增加；桥墩墩顶的横向振动加速度受行车速度影响较小，变化幅度较小。

由表5可以看出，在强度为0.1g的地震作用下轨道梁跨中相对位移随行车速度增加变化幅度较小；车体运行平稳性指标均小于2.75；但走行轮轮载变动系数受行车速度的影响较大，变化幅度较大，当列车运行速度大于40 km/h时，走行轮轮载变动系数大于0.65，需要引起注意。

4 结论

以悬挂式单轨试验线为对象，对悬挂式单轨车-桥系统在地震作用下的动力响应问题进行研究，系统地分析了不同地震波强度和不同行车速度对于车辆、轨道梁和桥墩的动力响应的影响，可得出如下主要结论。

(1)随着地震动强度的增大，悬挂式单轨车桥系统各振动响应均近似呈线性规律增加；桥墩墩顶振动加速度和轨道梁跨中横向振动加速度受地震波强度影响明显，变化幅度较大。轨道梁垂向振动加速度和车体振动加速度随地震动强度变化较小。

(2)悬挂式单轨车桥系统各项振动响应均随行车速度的增加而增大。其中各垂向振动加速度随行车速度的增加大致呈线性规律增加；走行轮轮载变动系数受行车速度的影响较大，变化幅度较大；桥墩墩顶横向振动加速度受行车速度影响较小，变化幅度较小。

(3)本文计算结果可为悬挂式单轨的抗震设计和地震作用下悬挂式单轨运行安全性和平稳性的评价提供参考。对于地震的行波效应和不同轨道梁结构的动力响应尚需进一步分析。