路基冻胀对CRTSⅢ型板式无砟轨道受力和变形的影响研究
徐新玉,崔建荣
(1.江苏联合职业技术学院苏州建设交通分院,江苏苏州 215104; 2.苏州大学轨道交通学院,江苏苏州 215131)
引言
无砟轨道以其少维修、高舒适度和强耐久性等优点在我国高速铁路中应用广泛[1-6],我国严寒地区的高速铁路里程已达5 500 km[7],然而严寒地区的路基冻胀问题不可避免[8-9],一旦发生路基冻胀必然影响无砟轨道的受力和耐久性。作为自主研发的CRTSⅢ型板式无砟轨道已在我国盘营等严寒地区应用,另外我国正承担设计的莫斯科至喀山高速铁路拟采用CRTSⅢ型板式无砟轨道。因此,研究路基冻胀对CRTSⅢ型板式无砟轨道结构受力的影响具有重要的理论意义和工程价值。
近年来,国内外学者开展了路基冻胀对无砟轨道的影响研究[10-19],Ma Fuxun等利用GPS分析了温度变化下路基冻胀的变化规律[10];赵国堂研究了严寒地区的路基冻胀特征,建立了路基冻胀变形与CRTSⅠ型板式无砟轨道不平顺的对应关系,分析了路基冻胀对无砟轨道受力的影响,提出了严寒地区无砟轨道路基冻胀管理标准的确定方法[11-12];王功博等基于现场监测数据,分析了路基冻胀的变形特征及过程[13];蔡小培等通过建立CRTSⅠ型板式无砟轨道-路基空间耦合有限元模型,分析了不同路基冻胀条件下轨道结构的变形和层间离缝特征[14];李娟[15]、郭毅[16]和赵文博[17]分别研究了高速铁路路基冻胀对CRTSⅠ型板式无砟轨道结构静、动力学的影响,并提出了轨道结构破坏时对应的路基冻胀限值;向俊等研究了路基冻胀-融化-沉降循环作用对板式无砟轨道变形和受力的影响[18];杨国涛等基于动力分析,确定了CRTSⅢ型板式无砟轨道路基冻胀的控制标准[19]。现有研究成果主要针对CRTSⅠ型板式无砟轨道开展研究,但是关于路基冻胀对CRTSⅢ型板式无砟轨道受力和变形的影响缺乏研究。
本文基于有限元方法,以我国CRTSⅢ型板式无砟轨道为研究对象,建立CRTSⅢ型板式无砟轨道-路基空间耦合有限元模型,分析了路基冻胀位置、冻胀幅值和冻胀波长对无砟轨道结构受力和变形的影响,从而为严寒地区CRTSⅢ型板式无砟轨道路基冻胀变形控制提供理论支撑。
1 CRTSⅢ型板式无砟轨道路基冻胀计算模型及参数
1.1 有限元模型
路基上CRTSⅢ型板式无砟轨道由钢轨、扣件系统、预制轨道板、自密实混凝土调整层、隔离层和混凝土底座板组成[20]。建立有限元模型时,钢轨采用梁单元模拟,扣件系统采用线性弹簧单元模拟,轨道板、自密实混凝土、隔离层、底座板和路基基床表层均采用实体单元模拟,由于CRTSⅢ型板式无砟轨道的轨道板与自密实混凝土层采用门型钢筋连接,故模型中轨道板与自密实混凝土层间采用共用节点处理。考虑路基冻胀时自密实混凝土层与隔离层、隔离层与底座板、底座板与路基基床表层间可能产生离缝,模型中自密实混凝土层与隔离层、隔离层与底座板、底座板与路基基床表层间采用接触单元来模拟两者之间的黏结作用,建立的CRTSⅢ型板式无砟轨道有限元模型如图1所示。
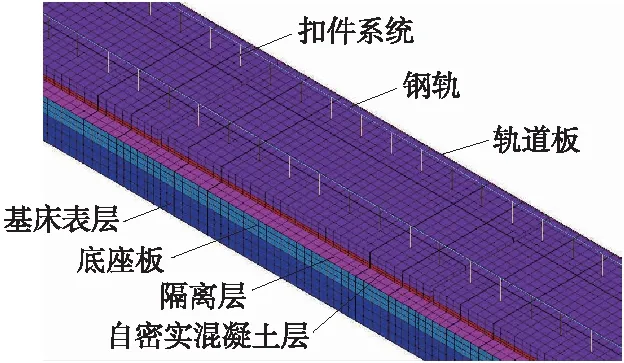
图1 CRTSⅢ型板式无砟轨道-路基空间耦合有限元模型
1.2 计算参数
有限元模型中,钢轨采用CH60N钢轨,扣件采用WJ-8B型扣件,扣件间距取为0.63 m,扣件系统的纵向、横向和垂向的刚度分别取为30,30 kN/mm和50 kN/mm。轨道板为C60混凝土,宽度为2.5 m,厚度0.2 m,长度为5.6 m,弹性模量为36.0 GPa;自密实混凝土层为C40混凝土,宽度为2.5 m,厚度为0.09 m,长度为5.6 m,弹性模量为32.5 GPa;底座板为C40混凝土,宽度为3.1 m,厚度为0.3 m,长度为16.99 m,弹性模量为32.5 GPa,路基基床表层弹性模量取120 MPa,宽度为3.1 m,厚度取为0.5 m。
路基冻胀采用余弦形式[14],分别作用在底座板接缝附近(工况A)、轨道板板缝附近(工况B)和底座板中间附近(工况C),路基冻胀作用位置如图2所示。

图2 冻胀作用位置
2 路基冻胀对轨道变形和受力的影响
2.1 路基冻胀位置的影响
当路基冻胀曲线波长为20 m,冻胀幅值为10 mm时,不同路基冻胀位置下轨道结构各层的变形如图3所示。
从图3可见,当路基发生冻胀时,轨道结构各层变形具有一定的跟随性,钢轨、自密实混凝土层、底座板的垂向变形逐渐减小。当路基冻胀作用在不同位置时,自密实混凝土层与底座板、底座板与路基基床表层的层间离缝主要发生在路基冻胀波峰和波底。工况A下,自密实混凝土层与底座板、底座板与路基基床表层的最大离缝值分别为0.133 mm和0.741 mm。工况B下自密实混凝土层与底座板、底座板与路基基床表层的最大离缝值分别为0.180 mm和0.750 mm。工况C下自密实混凝土层与底座板、底座板与路基基床表层的最大离缝值分别为0.229 mm和0.976 mm。可见,路基冻胀作用下,底座板与路基基床表层的离缝值远大于自密实混凝土层与底座板的离缝值。
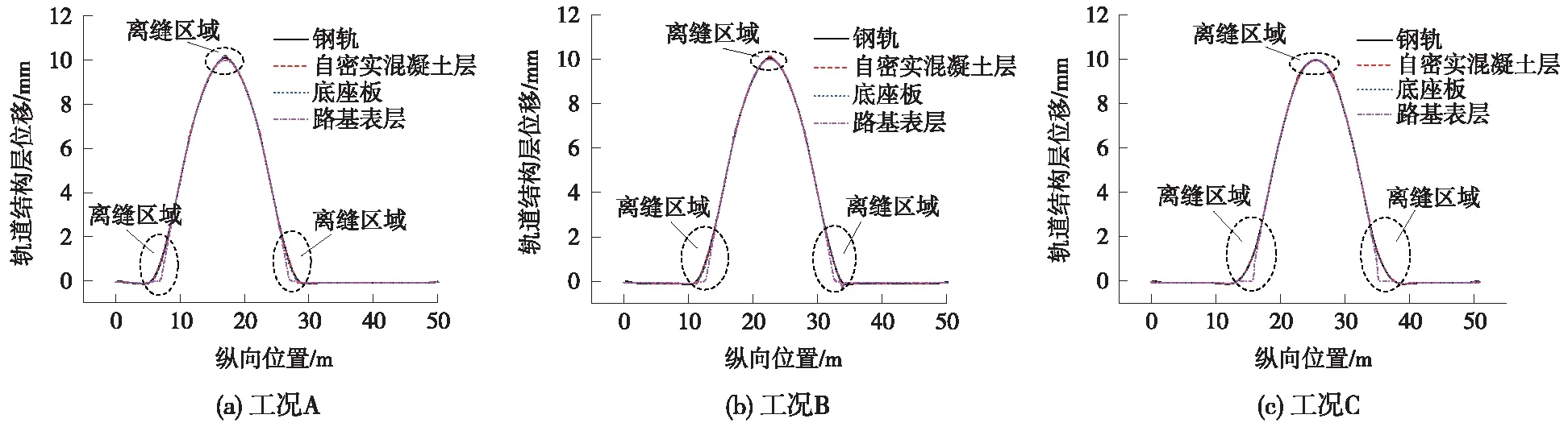
图3 不同冻胀位置下轨道结构位移曲线
不同路基冻胀位置下,轨道结构各层的应力如表1所示。
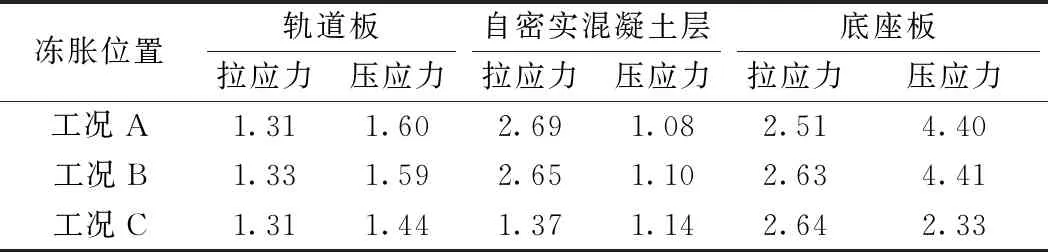
表1 不同冻胀位置下轨道结构各层的最大应力 MPa
从表1可见,轨道结构受力与路基冻胀作用位置有关,路基冻胀发生在位置A和位置B时,轨道板和自密实混凝土层所受应力大于冻胀作用于位置C。路基冻胀发生在位置B和位置C时,底座板所受拉应力大于冻胀发生在位置A处,说明路基冻胀发生在底座板下部时对底座板受力更加不利。
由于当路基冻胀发生在底座板板中时,轨道结构层间离缝和底座板受力均最大,故下文均以路基冻胀发生在底座板板中进行分析。
2.2 路基冻胀幅值的影响
当路基冻胀波长为20 m,冻胀幅值分别取为2,5,8,10,15 mm和20 mm时,不同路基冻胀幅值下轨道结构各层的位移和应力分别如表2、表3所示。
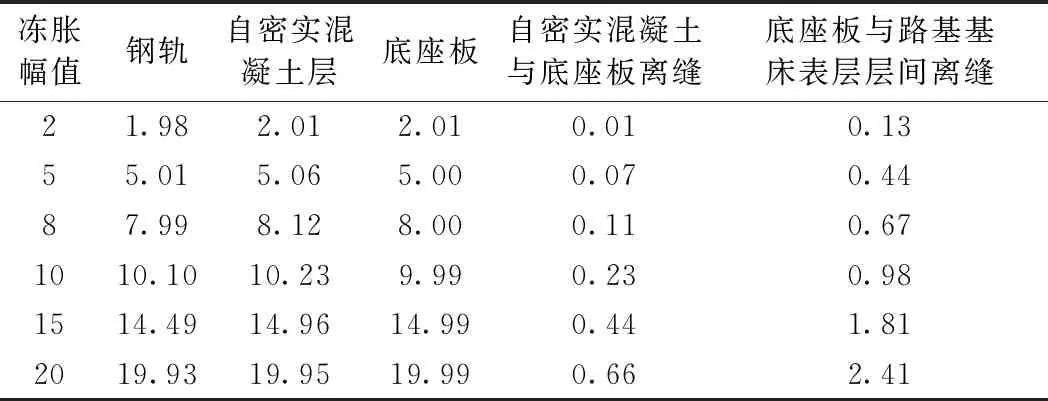
表2 不同冻胀幅值下轨道结构各层的位移 mm
从表2可知,轨道结构各层位移、层间离缝值均随路基冻胀幅值的增大而增大。根据工程实践,当离缝值大于1.0 mm时,认为轨道结构出现脱空现象,会对行车产生不利影响[12]。当路基冻胀幅值为20 mm时,自密实混凝土层与底座板的离缝值为0.66 mm,可认为不存在脱空现象。当路基冻胀幅值为10 mm时,底座板与路基基床表层的层间离缝达到0.98 mm,接近层间离缝限值1 mm。考虑轨道结构的层间离缝,认为路基冻胀波长为20 m,冻胀幅值不应超过10 mm。
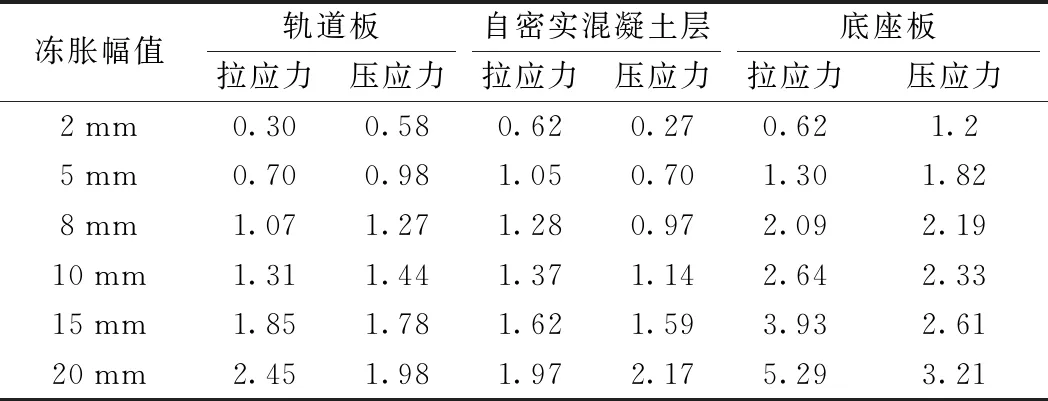
表3 不同冻胀幅值下轨道结构各层的最大应力 MPa
从表3可知,轨道结构各层的受力均随路基冻胀幅值的增大而增大,且相同条件下,底座板所受拉应力最大,因此路基冻胀幅值受底座板所受拉应力控制。根据相关规范可知,底座板和自密实混凝土的拉应力允许值为2.7 MPa,轨道板混凝土的拉应力允许值为3.5 MPa。当路基冻胀波长为20 m,冻胀幅值为10 mm时,底座板所受拉应力为2.64 MPa,接近底座板混凝土拉应力允许值,因此从底座板受力的角度考虑,当路基冻胀波长为20 m时,冻胀幅值不应大于10 mm。
2.3 路基冻胀波长的影响
当路基冻胀幅值为10 mm时,冻胀波长从5 m变化至30 m时,轨道结构的层间离缝变化如图4所示。

图4 轨道结构各层的层间离缝
从图4可知,轨道结构各层的层间离缝值随路基冻胀波长的增大而减小,且底座板与路基基床表层的层间离缝值远大于自密实混凝土与底座板的层间离缝,因此,应根据底座板与路基基床表层的层间离缝值来确定路基冻胀波长对应的冻胀幅值限值。
由于在路基冻胀作用下轨道结构各层的压应力远小于混凝土的抗压强度,路基冻胀幅值主要受拉应力控制,因此仅列出轨道结构各层拉应力随路基冻胀波长的变化,如图5所示。
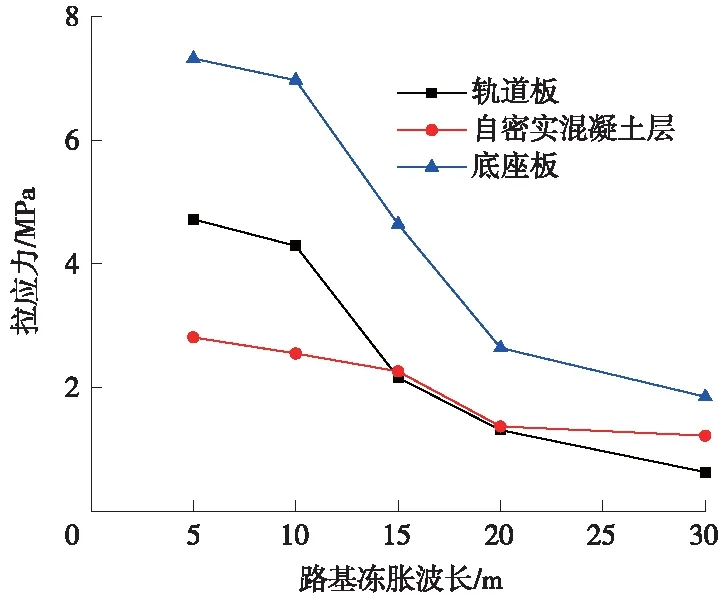
图5 轨道结构各层拉应力
从图5可知,轨道结构各层拉应力随路基冻胀波长的增大而减小。当路基冻胀幅值为10 mm时,路基冻胀波长小于20 m时,底座板所受拉应力将大于底座板拉应力允许值,当路基冻胀幅值为10 mm时,路基冻胀波长应≮20 m。
2.4 路基冻胀幅值限值
路基冻胀幅值主要由底座板与路基基床表层的离缝值、底座板拉应力控制,路基冻胀作用于底座板板中时,不同路基冻胀波长和冻胀幅值下底座板与路基基床表层的离缝值、底座板拉应力变化如图6所示。
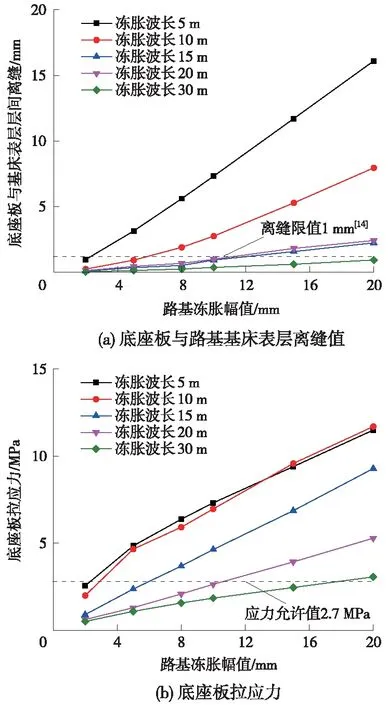
图6 路基冻胀幅值限值
从图6可知,当路基冻胀波长一定时,底座板与路基基床表层的层间离缝和底座板拉应力均随路基冻胀幅值的增大而增大;当冻胀幅值一定时,底座板与路基基床表层的层间离缝和底座板拉应力均随路基冻胀波长的增大而增大。综合考虑底座板与路基基床表层的离缝限值和底座板混凝土允许拉应力限值,当路基冻胀波长为5 m时,路基冻胀幅值应≯2 mm;当路基冻胀波长为10~15 m时,冻胀幅值应<5 mm;路基冻胀波长为20 m时,冻胀幅值≯10 mm;路基冻胀波长为30 m时,路基冻胀幅值≯15 mm。从静力角度考虑,路基冻胀幅值限值随冻胀波长的增大而增大。从轨道平顺性的角度,路基冻胀幅值越大,产生的不平顺幅值越大,此时应综合考虑行车安全性和平稳性来确定长波下的冻胀幅值。
3 结论
通过建立CRTSⅢ型板式无砟轨道-路基空间耦合模型,研究了路基冻胀位置、冻胀幅值和冻胀波长对无砟轨道受力和变形的影响,得到如下结论。
(1)路基冻胀作用位置对轨道结构各层的变形和受力影响较大;当路基冻胀发生在底座板板中时,轨道结构层间离缝和底座板受力均最大。
(2)随着路基冻胀幅值的增大,轨道结构各层的变形和应力均增大;当冻胀波长为20 m,冻胀幅值超过10 mm时,底座板与路基基床表层的层间离缝值、底座板拉应力接近限值,应及时进行冻胀防治。
(3)随着路基冻胀波长的增加,轨道结构的层间离缝和拉应力随之减小;路基冻胀波长增大对减小层间离缝和轨道受力有利。
(4)从轨道静力分析可知,路基冻胀幅值限值随路基冻胀波长的增大而增大。

