加劲长悬臂板混凝土箱梁施工阶段受力状态优化

宋旭明 李梦然 赖明苑 唐冕

(中南大学 土木工程学院，湖南 长沙 410075)

加劲长悬臂板混凝土箱梁能增加桥面宽度，减少材料的使用量，满足受力性能和经济性的要求，在公路桥梁中越来越受到工程技术人员的青睐。随着加劲长悬臂板预应力混凝土箱梁桥的大量修建，部分桥梁在施工过程中出现了桥面板开裂现象，影响了桥梁的耐久性及运营阶段的使用性能。因此，对加劲长悬臂板混凝土箱梁施工阶段的受力性能进行研究是我国桥梁建设的迫切需要[1- 2]。长悬臂板的悬臂长达7～9 m，受箱梁腹板和加劲挑梁的约束，处于复杂的纵横向传力状态，由于“剪力滞后”的影响，箱梁腹板附近配置的纵向预应力钢筋的压力难以传递到长悬臂板翼缘端部，是导致长悬臂板开裂的重要因素[3- 5]。目前，国内外学者对长悬臂板的受力以及箱梁剪力滞效应进行了大量的研究[6- 7]。Natário等[8]发现长悬臂预应力混凝土箱梁翼缘板宽度的增加会导致受力复杂，致使翼缘板配筋不足，从而使翼缘板处产生很多裂缝；他们认为这些裂缝的产生大部分是由于在集中荷载下箱梁翼缘板内缺少抗剪钢筋或抗剪钢筋不足，剪切破坏是裂缝产生的主要原因。陈千书等[9]依托某矮塔斜拉桥，用ANSYS软件建立有限元模型，精确模拟了斜拉桥的悬臂施工过程，得出结论：最大悬臂阶段的顶板剪力滞效应沿悬臂方向由正剪力滞效应过渡为负剪力滞效应；随着悬臂施工过程的推进，剪力滞系数趋于稳定。徐弘亮等[10]利用差分法分析挂篮移动和混凝土浇筑过程中的剪力滞效应，并与工程实测数据进行对比，发现按施工过程计算混凝土自重产生的剪力滞效应大于最大悬臂状态自重一次累加的剪力滞效应。祝明桥[11]对大比例悬臂梯形截面混凝土薄壁连续箱梁在弹性范围内的剪力滞效应进行了试验研究，并分析了各级荷载下的中间支座和跨中截面荷载-挠度曲线，发现混凝土薄壁连续箱梁无论是中间支座处，还是跨中截面处，均存在正剪力滞效应。蔺鹏臻等[12]研究了3种布束方式综合作用下箱梁的剪力滞效应，基于能量变分原理，结合预应力等效荷载法，建立了有效计算箱梁在直线、折线和曲线预应力布束方式下的剪力滞效应的理论解析方法。然而，现有研究中，长悬臂板的形式较为单一，大多为普通长悬臂板，较少涉及加劲长悬臂板。在加劲长悬臂板的研究方面，学者们更多地关注钢挑梁加劲[13],对于混凝土挑梁加劲方面的研究还不充分，特别是对加劲长悬臂板施工阶段的剪力滞效应未进行针对性的研究[14]。有鉴于此，文中以一座大跨径矮塔斜拉桥为基础，通过有限元软件分析并验证其施工阶段的剪力滞效应，并进一步探究不同工况下的截面受力状态，以期为指导工程实践、制定类似截面桥梁的裂缝控制措施提供参考。

1 工程概况及有限元模型

1.1 工程背景

本课题的依托工程——衡阳东洲湘江大桥为三塔四跨矮塔斜拉预应力混凝土斜拉桥，截面形式为加劲长悬臂板箱梁。该桥采用塔、梁、墩固结的刚构体系。主桥全长660 m，孔径布置为120 m+2×210 m+120 m。斜拉索为单索面双排索，布置在主梁中央分隔带处。塔根两侧无索区长35.0 m，120 m边跨无索区长25.0 m，中跨无索区长20.0 m。全桥共3个索塔，索塔塔高35 m，主塔截面顺桥向等宽段厚5 m，塔底10 m范围内宽度由5 m渐变到6 m；主塔横桥向3 m宽。主梁为预应力混凝土变截面箱梁，采用整幅式斜腹板单箱三室截面。箱梁顶板宽3 850 cm，顶板中间300 cm宽处(拉索区)为平坡，两侧采用2%双向横坡；跨中梁高4.1 m(含中央带凸出厚度0.3 m)，主塔根部梁高7.3 m；箱梁采用大悬臂构造，悬臂长825 cm，板厚为线性变化，板端部厚20 cm，根部板厚50 cm，悬臂翼缘支撑在40 cm厚的挑梁上，挑梁间距为2.2～4.0 m。桥型布置如图1所示。

图1 东洲湘江大桥主桥桥型图(单位：m)Fig.1 Diagram of Dongzhou Xiangjiang Bridge’s main bridge type(Unit:m)

施工过程中发现，部分节段浇筑后初期混凝土质量表现较好，但一两个节段之后出现开裂现象，并且裂缝主要出现在节段线处悬臂板上，越靠近悬臂端部裂缝分布越密集。

1.2 有限元模型

利用MIDAS FEA建立桥梁0#-10#悬浇过程中的空间块体元有限元模型，考虑到结构的对称性并为了尽量减小模型规模，仅建立1/4模型。模型共计478 106个块体元、461 997个节点，截面对称位置采用对称约束，并按照实际工程布置三向(纵向、横向、竖向)预应力筋，预应力筋张拉的先后顺序为：纵向预应力束→横向预应力束→竖向预应力束，如图2所示。

2 剪力滞效应分析及模型验算

2.1 剪力滞效应分析

施工阶段的主要荷载工况有自重作用、预应力作用和拉索力作用。为研究施工阶段加劲长悬臂板的剪力滞效应，定义以下两种荷载工况对长悬臂板局部纵向正应力分布情况进行分析：工况1，自重作用；工况2，纵向预应力作用。因拉索力作用与预应力作用相近，故不将其单独作为一种工况进行讨论。

图2 节段块体元有限元模型Fig.2 Finite element model of segmental block

2.1.1 工况1下的剪力滞效应

从计算截面中选取几个典型截面进行分析可知：大部分节段线处的上下翼缘剪力滞效应并不明显；而桥塔处及悬臂端截面呈现明显的剪力滞效应，其上下翼缘纵向正应力分布如图3所示。

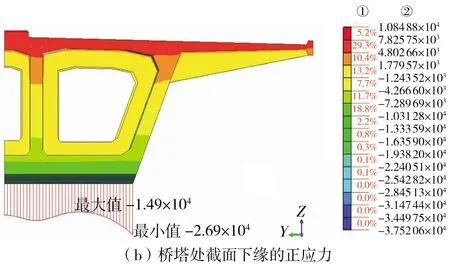
右上角数列①表示位于连续两个应力数值范围内 的数值所占总体的百分比，数列②表示应力值

2.1.2 工况2下的剪力滞效应

由选取的典型截面上下翼缘纵向正应力分析可知，预应力筋作用位置对结构应力影响很大，作用点局部出现较大应力。桥塔处截面离预应力筋锚固点较远，应力比较均匀，无明显剪力滞效应，其他截面尤其是节段线位置截面的剪力滞效应明显，其上下缘纵向正应力分布如图4所示。

右上角数列①表示位于连续两个应力数值范围内 的数值所占总体的百分比，数列②表示应力值

2.2 有限元模型验证

为了对施工阶段主梁的剪力滞效应进行分析，在衡阳东洲湘江大桥施工过程中对部分节段进行应力测试，测试断面设置在11#墩距0#-1#节段线、1#-2#节段线、2#-3#节段线10 cm截面处。每个断面布置18个应变测点，应变计高度距相应顶底板约8 cm，在横截面上的布置如图5所示。随着施工过程的推进，对10个工况进行测试，测试内容如表1所示。

图5 1#断面应变计布置位置(单位：cm)

施工阶段截面所受外界作用以纵向受力为主，本节仅分析各施工工况下测试断面的纵向正应力。

表1 测试工况内容Table 1 Contents of test cases

为了更为清晰地进行对照，现将部分工况和测点的计算及测试结果列于表2。全部10个工况的测试结果与有限元计算结果如图6所示。

表2 不同工况下的有限元计算值和实测值(部分)Table 2 Part of finite element calculation values and measured values in different test cases

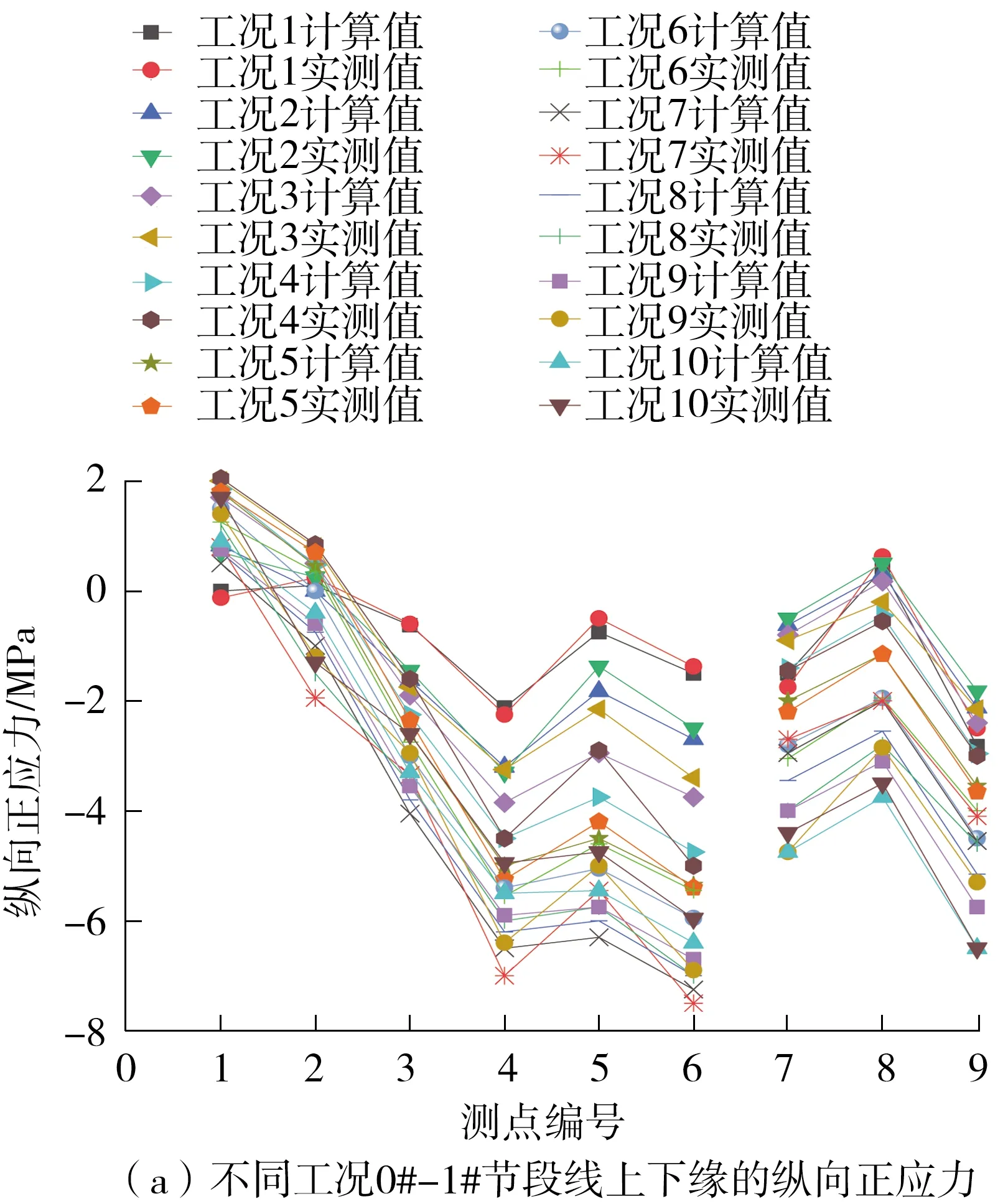
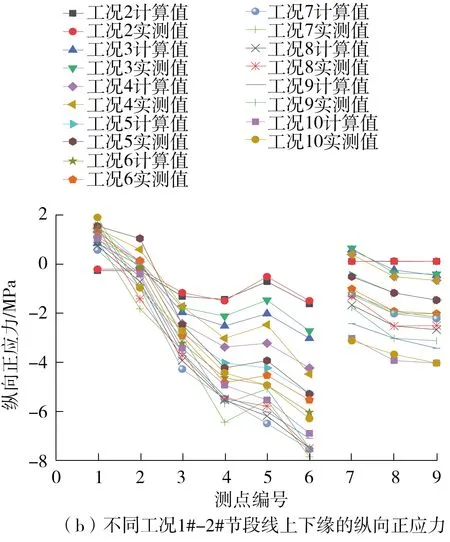
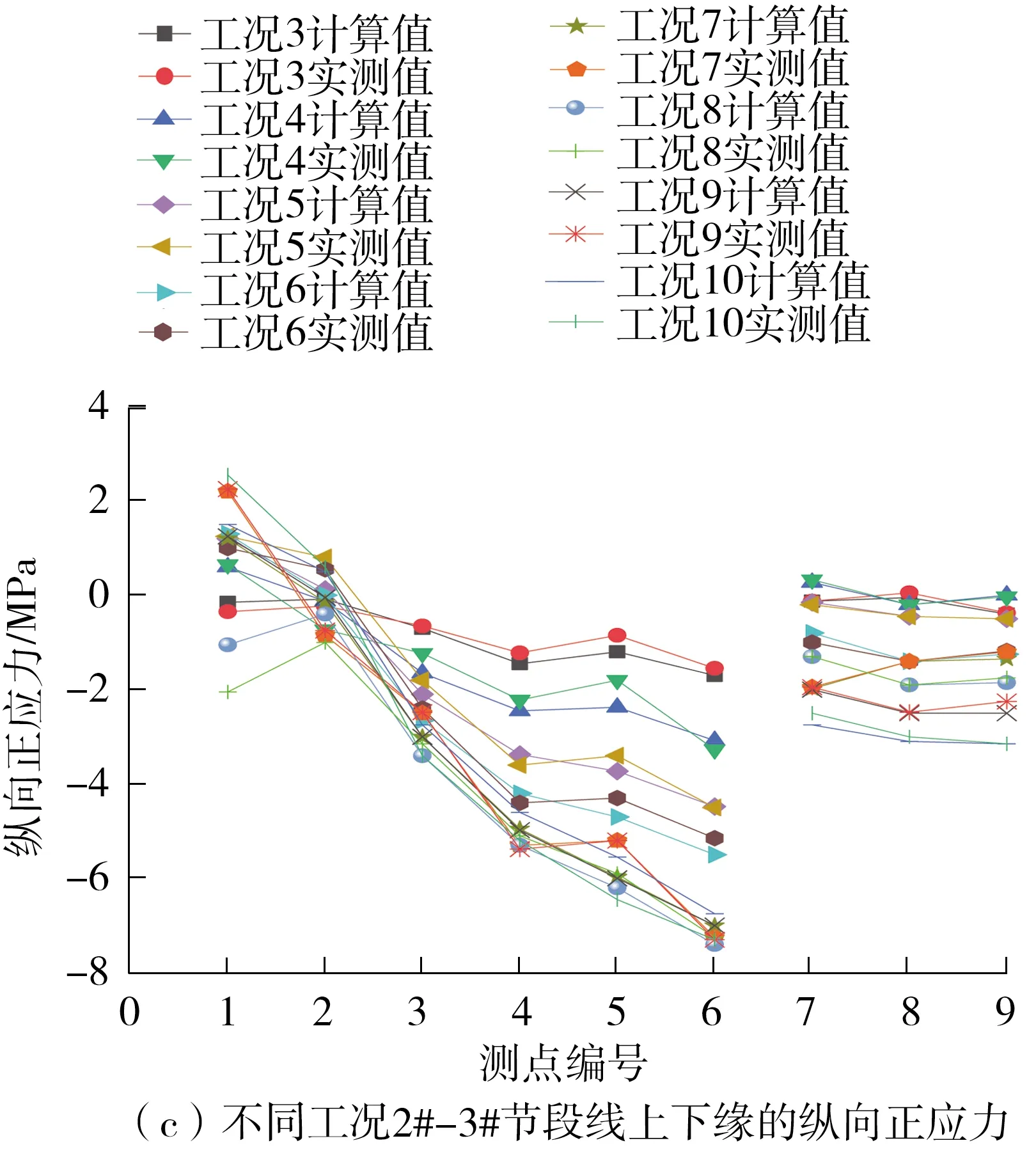
图6 有限元计算值与实测值的对比

通过对10个工况下两种数值的对比分析发现：除个别测点有偏差外，有限元模型计算值与实测值基本吻合，说明所建立的有限元模型能正确反映剪力滞效应下的应力状态；但在个别测点计算值与实测值有偏差，说明目前的有限元模型尚不能完全精确模拟结构的实际受力状况。

分析结果表明，加劲长悬臂板箱梁的剪力滞效应使悬臂端的压应力储备不足，极有可能在外荷载作用下产生大于抗拉强度的拉应力，从而产生裂缝。为了减小剪力滞效应的不利影响，可在悬臂端另外配置预应力钢筋，增大压应力储备，优化悬臂端的受力状态。

3 施工工序对加劲长悬臂板受力性能的影响

除剪力滞效应之外，长悬臂板出现裂缝与混凝土节段浇筑的龄期差、横向预应力张拉时的泊松效应也有一定关系[15]。后浇筑节段的纵向预应力可通过一定的传递长度作用于已浇筑节段的悬臂板，考虑到混凝土箱梁配置了三向预应力筋，因此拟通过改变预应力筋张拉顺序及滞后张拉横向预应力钢筋的方式来改善施工阶段出现裂缝的问题。

根据之前的剪力滞效应分析，考虑到悬臂端部的压应力储备较小，该桥在悬臂板上额外配置纵向预应力筋。纵向和悬臂板加设的预应力筋布置如图7所示，在悬臂板额外增加了预应力筋J1-J2、J1a-J2a。J1、J2采用的是JL32高强精扎螺纹钢筋，张拉控制应力为837 MPa；J1a、J2a采用的是3Φs15.2 mm预应力钢绞线，单端张拉，张拉控制应力为1 395 MPa。

图7 0#截面纵向、悬臂预应力钢筋布置图(单位：cm)

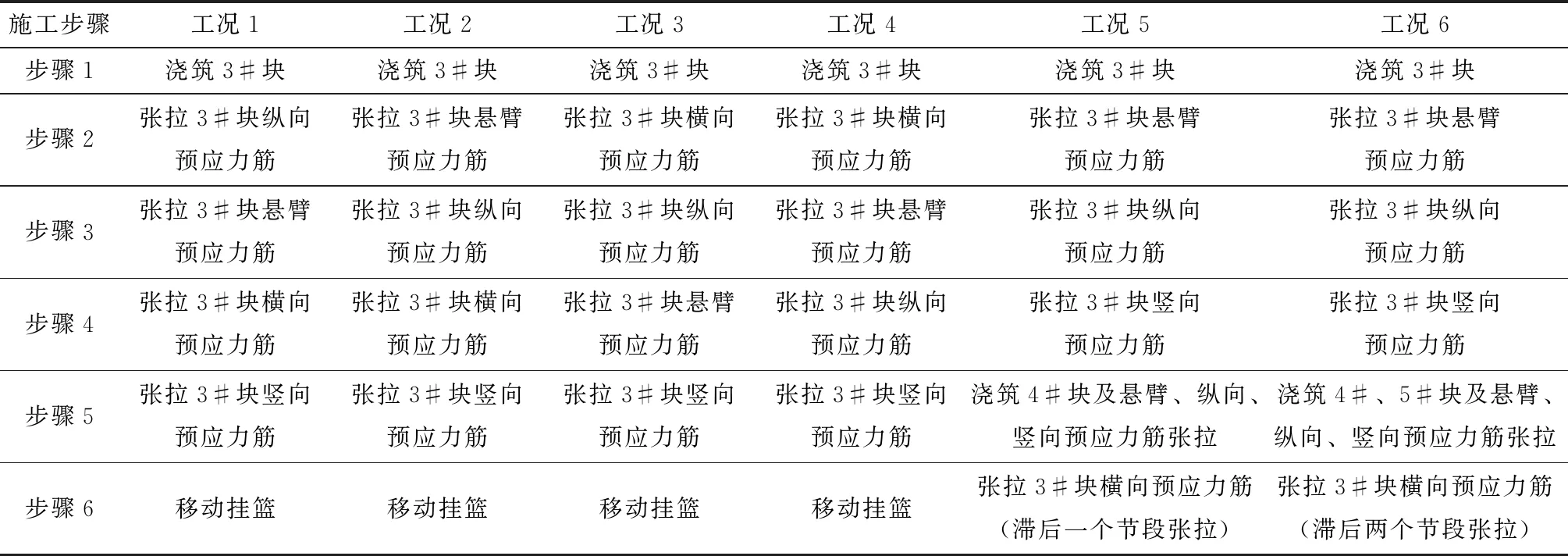
表3 各工况的施工步骤Table 3 Construction steps for each working condition

采取不同的预应力钢筋张拉次序及横向预应力钢筋滞后张拉方案，根据施工工艺拟定了6种工况，如表3所示。选取3个典型截面进行分析，分别为2#-3#节段线处截面Ⅰ-Ⅰ、3#节段中间截面Ⅱ-Ⅱ、3#挑梁处截面Ⅲ-Ⅲ。

3.1 截面Ⅰ-Ⅰ分析结果

分析截面Ⅰ-Ⅰ桥面板上缘的纵向正应力计算结果发现：在工况3、4中，张拉横向预应力筋，悬臂板端部出现了最大的拉应力，为0.432 MPa；工况3中张拉纵向预应力筋时还出现了较大的拉应力(0.417 MPa)；对比工况1、2，工况1先张拉纵向预应力筋，工况2先张拉悬臂预应力筋，工况2悬臂板压应力储备较大；对比工况2、5、6，其张拉次序依次为悬臂、纵向、横向，但工况2是同一个节段张拉，工况5是滞后一个节段张拉，工况6是滞后2个节段张拉；工况2中压应力最小，工况5中最大压应力为4.85 MPa，小于工况6的5.63 MPa。分析截面Ⅰ-Ⅰ桥面板下缘的纵向正应力发现：节段线桥面板上下缘的应力变化规律基本一致；对于桥面板下缘，工况3、4悬臂板端部出现了拉应力，并大于桥面板上缘。综上，对于节段线桥面板上下缘，应选择工况6，即悬臂→纵向→横向(滞后2个节段张拉)。工况6的上下缘纵向正应力如图8所示。

3.2 截面Ⅱ-Ⅱ分析结果

分析截面Ⅱ-Ⅱ桥面板上缘的纵向正应力计算结果发现：工况1至4中，步骤5、6的桥面板纵向正应力几乎相等，主要不同之处在于步骤2、3、4；相对于工况1、2，工况3、4出现了拉应力，最大拉应力出现在靠近悬臂板端部位置；工况1、2的纵向正应力均为压应力，但工况2的压应力较大；工况2、5、6中，工况2的压应力最小，工况5悬臂板端部的压应力储备较大。分析截面Ⅱ-Ⅱ桥面板下缘的纵向正应力计算结果发现：3#节段中间截面桥面板上下缘的应力变化规律基本一致；对于桥面板下缘，工况3、4中出现了拉应力，工况5、6的应力情况相差不大。综上，对于节段中间截面桥面板上下缘施工，应选择工况5，即悬臂→纵向→横向(滞后1个节段张拉)。工况5的上下缘纵向正应力如图9所示。

3.3 截面Ⅲ-Ⅲ分析结果

分析3#挑梁处截面Ⅲ-Ⅲ桥面板上缘的纵向正应力计算结果发现：工况1至6的纵向正应力均为压应力，无拉应力出现；由于挑梁的设置，该处截面桥面板的受力较合理，出现横向裂缝的可能性较低；工况1至4中，工况2的压应力较大；工况2、5、6中，工况2的压应力较小，工况6悬臂板的压应力储备较大。分析3#挑梁处截面Ⅲ-Ⅲ桥面板下缘的纵向正应力计算结果发现：挑梁处截面下缘应力不同于上缘应力，工况3、4中出现了拉应力，工况1、2的应力情况相当，工况5、6的最大压应力分别为9.366、9.964 MPa，比桥面板上缘大。综上，对于挑梁处截面，应选择工况5，即悬臂→纵向→横向(滞后一个节段张拉)。工况5的上下缘纵向正应力如图10所示。

综合对节段线处、挑梁中间截面及挑梁处截面在不同预应力筋张拉顺序和横向预应力钢筋滞后张拉工况下的桥面板上下缘纵向正应力的分析可知：工况3、4先张拉横向预应力筋，该步骤出现了较大的拉应力；而工况5、6滞后一两个节段张拉横向预应力筋可使得桥面板有较大的压应力储备，原因在于当张拉横向预应力筋时，混凝土节段横向受压，由于泊松效应，混凝土节段将纵向受拉，但滞后一个节段张拉时，后一节段悬臂板中施加的纵向预应力对前一个节段产生压力，加大了悬臂板中的预压应力储备。在实际工程中，将预应力筋张拉次序改为工况5，即悬臂→纵向→横向(滞后1个节段张拉)，并对悬臂板端部在工况5下的不同施工阶段进行了截面压应力测试，所得测试结果与计算结果的对比如表4所示。由表4可知，悬臂板端部在采用工况5之后，上下缘截面应力状态良好，压应力储备皆在3 MPa以上，且施工后期未发现悬臂板开裂现象，桥面板开裂的问题得到了有效解决。

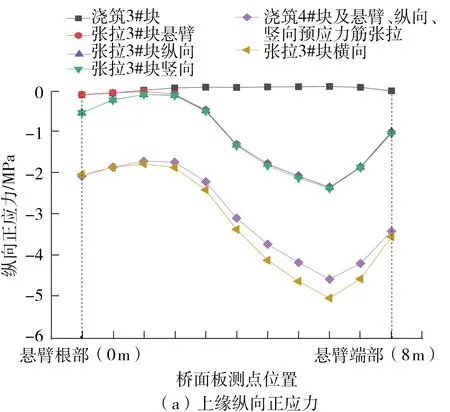
表4 工况5下悬臂板端部应力实测及计算结果Table 4 Test and calculation results of stress of cantilever plate end in working condition 5

4 结论

(1)在施工过程中，自重作用下大部分节段线处的剪力滞效应不明显，桥塔处及悬臂端截面呈现明显的剪力滞效应。

(2)在纵向预应力作用下，越靠近预应力作用点剪力滞效应越明显；桥塔因距离预应力筋锚固点较远，其应力均匀，无明显剪力滞效应。

(3)在加劲长悬臂板混凝土箱梁翼缘板额外配置纵向预应力筋可以增加截面压应力储备，改善施工阶段翼缘板出现裂缝的问题。

(4)综合对悬臂节段线、节段中间截面及挑梁处截面在不同预应力筋张拉顺序下桥面板上下缘纵向正应力的分析可知，先张拉横向预应力筋将使悬臂板中出现较大的拉应力；而滞后一两个节段张拉横向预应力筋可使桥面板有较大的压应力储备，故推荐采用悬臂→纵向→横向(滞后一个节段张拉)的张拉预应力筋顺序，以使截面内力状态得到优化。