熔融沉积工艺填充速度与分层厚度、喷头温度的 相互耦合作用

陈松茂 陈宇林

(华南理工大学 机械与汽车工程学院，广东 广州 510640)

熔融沉积成型(Fused Deposition Modeling，FDM)技术具有操作简单、材料利用率高、环境友好等优点，被广泛应用于医疗、模具、建筑等行业[1- 4]。然而，FDM因受聚合物材料粘弹特性、冷却收缩性等的影响，逐层打印台阶效应明显，制件尺寸精度、表面粗糙度及机械强度普遍不高，同时存在成型质量与打印效率相互矛盾的工艺性瓶颈。影响FDM制件成型质量与打印效率的主要工艺参数包括：模型切片分层厚度、填充速度、挤出速度、喷头温度、填充率等。在FDM中，高度方向是以所设定的分层厚度为最小单位逐步叠加的，不管是均匀分层[5]还是自适应分层，都不可避免地会产生一定程度的台阶效应。分层厚度的变化决定了喷头单位时间熔丝的挤出量，也影响了沉积熔丝的实际线宽和波动范围。填充速度过大时，熔丝冷却速度降低，将引起残余应力增大并导致制件更易出现翘曲变形；填充速度过低时，制件成型质量可得到保障，但同时降低了打印效率[6]。挤出速度的大小制约了喷嘴挤出熔丝材料的加热和冷却周期，容易引起已沉积材料不同程度的热梯度，最终影响制件的成型质量[7]。刚沉积的熔丝材料从喷头温度冷却至玻璃化转变温度时，会产生冷却收缩效应，不过由于时间较短，内应力累积较少；但当沉积熔丝材料从玻璃化温度冷却至室温时，时间较长，会受到周边或上下层熔丝循环的传热和冷却作用，引起不均匀的温度梯度，积累较多热内应力，导致制件翘曲变形和精度下降[8]。此外，分层厚度、填充速度、挤出速度、喷头温度等工艺参数在FDM中是相互制约的，明确它们之间的相互作用机制、实现工艺参数的准确控制，对提高FDM制件质量和打印效率尤为重要。其中，填充速度直接制约了FDM制件的成型精度和打印效率，国内外许多学者对此展开了一系列优化与控制方面的研究。

白石根[9]利用Matlab分析了3种尺寸模型的分层厚度与填充速度之间的相互作用，在单层切片轮廓中根据当前喷头运动轨迹与X轴的正向夹角，提出一种基于CAD模型外轮廓线自适应分层的分层填充速度自适应控制方法，推导了X、Y轴向填充速度的Clothoid曲线拟合函数来计算每一层熔丝的自适应填充速度，在保证FDM制件尺寸精度的同时提高了打印效率。Qin等[10]提出一种实时自适应超前速度控制算法，采用Hbot运动系统来减小FDM成型过程中的不稳定性及运动惯量。该算法与S曲线加减速模型结合使用，有效改善了制件的尺寸精度和表面粗糙度。Peng等[11]利用响应面法对包括填充速度、分层厚度和喷头温度在内的5个参数进行了多目标优化，取得了较小的尺寸误差、翘曲变形和较短的打印时间，实验结果显示：打印时间很大程度上取决于分层厚度和填充速度，分层厚度较大时，喷嘴作用在熔丝上的挤出力较小，若此时填充速度较大，则容易出现拉丝现象，熔丝难以粘附在表层上。Ognjan等[12]开发了一种称作定性筛选设计(DSD)的新统计方法，用于分析包括填充速度、分层厚度和喷头温度在内的5个工艺参数及其相互作用对聚乳酸(Polylactic Acid，PLA)试样最大弯曲力的影响，实验结果表明：低的喷头温度结合高的填充速度，会导致层与层之间粘合不良，并使制件表面光洁性变差。不过，该实验只设计了一种试样材料作为示例，不具备共性，需采用更多材料实例进行论证，同时还需解决双向交互作用的混淆和二次效应等问题。Ertay等[13]提出了一种成比例同步材料挤出速度和填充速度的工艺控制策略，通过采用填充速度优化算法，获取时间采样位置数据和轨迹轮廓，改善了FDM制件拐角和高曲率处的材料堆积问题；该策略还考虑了加热和挤出装置容量及喷头驱动的冲击、加速度和速度限制等问题，但是算法相对复杂，实现难度大。

目前的研究重点集中在探寻填充速度与其他工艺参数之间的优化组合或控制方法等方面，鲜有学者讨论FDM工艺参数之间的相互耦合作用对制件成型精度的影响。因此，文中以PLA材料为例，采用双变量实验方案以及方差分析、多元非线性回归分析手段，研究FDM工艺填充速度与分层厚度、喷头温度之间的相互耦合作用机制。以最低综合尺寸偏差为目标，通过分析填充速度与分层厚度、喷头温度的交互作用规律，推导构建填充速度与分层厚度、喷头温度相互耦合作用的半经验函数模型，实现对填充速度的优化控制，改善FDM制件的成型质量。

1 实验方法

1.1 参数选择

FDM成型过程中重要的工艺参数有层厚、喷头温度、填充速度、挤出速度、填充率、壁厚等。文中选择前3个参数为研究对象，原因如下：①本实验评价指标为尺寸精度，而填充率主要影响制件的力学性能；②实验设备中挤出速度与填充速度已同步；③尽管壁厚对尺寸精度有影响，但根据以往经验可知，在未设置偏置时设备外壳数越多，其X、Y方向偏差越大，并且效率也越低，因此，为简化实验，选择单外壳即可；④填充速度与喷头温度、层厚之间的耦合关系影响了应力分布和变形等[6- 7]，具体而言这种耦合关系体现在热收缩、喷嘴挤出不均匀和挤出丝的拉伸等过程中，为了寻找填充速度的控制规律，有必要对这种耦合关系加以研究；⑤因多因素耦合机制复杂，文中以已选参数作为试点进行前期研究，其他参数的耦合作用暂时不做考虑，留待后期实验中进一步探讨。

1.2 试样材料及规格

采用国产某型号PLA丝材，直径为φ(1.75±0.02) mm，熔化温度范围为190～220 ℃，密度为(1.25±0.05) g/cm3。

研究填充速度(v)与分层厚度(t)和喷头温度(T)的关系时，设计了两种尺寸规格的试样，分别为60 mm×15 mm×6 mm的长方体(Ⅰ型试样)和30 mm×30 mm×6 mm的长方体(Ⅱ型试样)。两种试样每一层的面积相同，统一定义长、宽、高分别为X、Y、Z方向。

1.3 设备仪器

FDM设备采用国产高诺A001桌面型打印机，喷嘴孔径为φ0.4 mm，分层厚度为0.05～0.40 mm，最高填充速度为200 mm/s，X、Y轴定位精度均为0.025 0 mm，Z轴定位精度为0.012 5 mm。测量仪器选用锌合金电子数显卡尺，型号为LF170，分辨率为0.01 mm。

1.4 评价指标

选取尺寸精度作为FDM制件的质量评价指标。尺寸精度由尺寸偏差来评估，采用误差的绝对值形式。等效尺寸偏差e分别由各自X、Y、Z这3个方向的尺寸偏差计算获得，具体公式如下：

(1)

e=|Xe|+|Ye|+|Ze|

(2)

式中，Xe、Ye、Ze分别为X、Y、Z方向的尺寸偏差，Xi、Yi、Zi为试样尺寸的测量平均值，X、Y、Z为尺寸的理论设计值。

1.5 测量方案

为保证实验数据准确可靠，统一采用图1所示的卡尺测量点方案。除Ⅰ型试样长边尺寸是夹取长边两端中间测量3次外，其余尺寸均选择3个四等分位置各测量1次，再取平均值作为测量值。测量并记录各Xi、Yi、Zi值，将其取平均值并代入式(1)计算获得尺寸偏差Xe、Ye、Ze。最后，根据式(2)计算得到对应的等效尺寸偏差。

图1 卡尺测量点示意图Fig.1 Schematic diagram of measuring points of the caliper

1.6 实验方案

采用双变量实验方案，以最低等效尺寸偏差为目标，将填充速度分别与分层厚度、喷头温度组合，对Ⅰ、Ⅱ型试样进行多组的打印实验。设定每组实验的变量为填充速度(v)+分层厚度(t)或者填充速度(v)+喷头温度(T)，同时规定当t和T中一个为变量时，另一个保持中值不变，分别构建v与t、T的函数关系式，实验重复3次。然后，进行方差分析，对比t、T对v的影响以及v和t、v和T之间的相互耦合作用。最后，利用Matlab R2016b进行曲面拟合及回归分析，获得v同时与t、T的三元耦合作用函数关系式，作为填充速度v的控制函数。

设定填充速度的取值为20、30、40、50、60、70 m/s，分层厚度的取值为0.10、0.15、0.20、0.25、0.30 mm，喷头温度的取值为184、192、200、208、216 ℃。除了分层厚度、喷头温度和填充速度以外的所有参数进行固化处理(过程略)，其余工艺参数采用FDM设备自带控制软件的默认值(见表1)。

表1 其他FDM工艺参数的设定值Table 1 Default values of other FDM process parameters

2 结果分析与讨论

2.1 填充速度与分层厚度、喷头温度的二元相互作用

2.1.1 Ⅰ型试样分析

填充速度分别与分层厚度及喷头温度之间的二元相互作用规律可由测量得到的等效尺寸偏差分析获得。不同分层厚度下Ⅰ型试样填充速度与等效尺寸偏差的关系如图2(a)所示，不同喷头温度下的关系则如图2(b)所示。设同一分层厚度下使等效尺寸偏差最小的填充速度为该分层厚度下的最优填充速度v0，同一喷头温度下使等效尺寸偏差最小的填充速度为该喷头温度下的最优填充速度v1，则根据测量数据计算可得5个分层厚度下对应的v0依次为20、20、70、70、20 mm/s，5个喷头温度下对应的v1依次为40、20、60、50、60 mm/s。

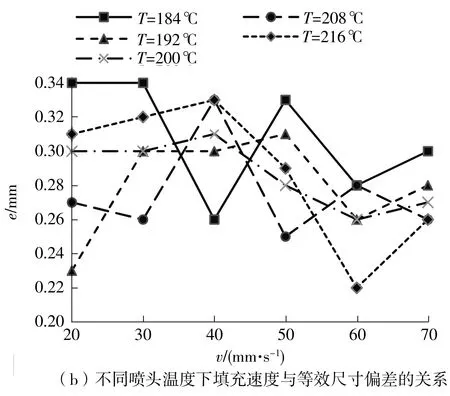
图2 Ⅰ型试样分析结果Fig.2 Analysis results of Sample Ⅰ

分别对v-t、v-T实验获得的等效尺寸偏差的各向占比进行计算和对比分析。结果显示：Xe约占60%，占主导地位；Ye和Ze约合占40%。这是因为Ⅰ型试样的X方向作为长边，其理论值为宽边的4倍、厚边的10倍，由冷却收缩引起的尺寸偏差更严重，Xe<0；而Y方向作为宽边，其收缩将在一定程度上受到X方向抑制，加上弹性回复等物理过程的综合作用，实际尺寸大概率高于理论值，即Ye>0，且比Xe更接近0；而Ze均大于0，其绝对值介于Xe和Ye之间，这是因为FDM导致Z方向上的收缩现象表现较弱[14]。

按照20、20、70、70、20 mm/s的v0值，喷头温度为200 ℃时v0与分层厚度t的曲线拟合三次式为

(3)

对应等效尺寸偏差的精度预测函数如式(4)所示，其函数幅值在0.32 mm以下：

e=-1.33×10t3+1.63×10t2-4.78t+6.46×10

(4)

按照40、20、60、50、60 mm/s的v1值，分层厚度为0.2 mm时v1与喷头温度T的曲线拟合三次式为

(5)

对应等效尺寸偏差的精度预测函数如式(6)所示，其函数幅值在0.26 mm以下：

e=-1.30×10-5T3+7.77×10-3T2-1.54T+

1.02×102

(6)

分层厚度与填充速度交互作用对等效尺寸偏差的方差分析结果如表2所示。其中，实验重复次数为3，速度水平数为6，分层厚度水平数为5。结果表明：Ⅰ型试样中填充速度和分层厚度对尺寸精度的影响显著，同时两者相互作用的影响也很明显，充分说明在熔融沉积过程中对填充速度与分层厚度进行联合控制是很有必要的。

表2 Ⅰ型试样的v-t关系方差分析结果Table 2 v-t ANOVA results of Sample Ⅰ

1)括号内数值表示置信度，下同。

喷头温度与填充速度交互作用对等效尺寸偏差的方差分析结果如表3所示。不同于表2的是，填充速度在99%的置信度下影响不显著，且喷头温度的显著性不高，但二者交互作用的影响非常显著，这同样说明了熔融沉积过程中对填充速度与喷头温度进行联合控制的必要性。

表3 Ⅰ型试样的v-T方差分析结果Table 3 v-T ANOVA results of Sample Ⅰ

2.1.2 Ⅱ型试样分析

不同分层厚度下Ⅱ型试样填充速度与等效尺寸偏差的关系如图3(a)所示，不同喷头温度下的关系则如图3(b)所示。5个分层厚度下对应的v0依次为20、70、70、70、70 mm/s，5个喷头温度下对应的v1依次为30、30、50、60、60 mm/s。

图3 Ⅱ型试样分析结果Fig.3 Analysis results of Sample Ⅱ

等效尺寸偏差中各向占比的计算结果为：Xe和Ye约合占50%，Ze占50%。其中，X方向尺寸偏差稍大于Y方向尺寸偏差，这个差异是由于两个方向受热不均造成的。占比最大的是Ze，表明最优填充速度将更大程度地以Z方向为依据，而Z方向的最优速度与v0高度重合。

按照20、70、70、70、70 mm/s的v0值，喷头温度为200 ℃时v0与分层厚度t的曲线拟合三次式为

(7)

对应等效尺寸偏差的精度预测函数如式(8)所示，其函数幅值在0.28 mm以下：

e=2.00×10t3-7.43t2-2.79×10-1t+3.62×10-1

(8)

按照30、30、50、60、60 mm/s的v1值，分层厚度为0.2 mm时v1与喷头温度T的曲线拟合三次式为

(9)

对应等效尺寸偏差的精度预测函数如式(10)所示，其函数幅值在0.17 mm以下：

e=-3.26×10-6T3+2.04×10-3T2-4.26×

10-1T+2.97×10

(10)

分层厚度与填充速度交互作用对等效尺寸偏差的方差分析结果如表4所示。由表4可知：Ⅱ型试样中填充速度与分层厚度对尺寸精度的影响依然显著，且二者交互作用的影响也很明显，这与Ⅰ型试样的结果一致。但因受到喷头移动加速度的限制，有限距离内会削弱填充速度的影响，采用99%的置信度时填充速度的影响不是很显著。

喷头温度与填充速度相互关系对等效尺寸偏差的方差分析如表5所示。Ⅱ型试样喷头温度对尺寸精度影响的显著性高于Ⅰ型试样，这是因为在打印Ⅱ型试样时喷头的热量更集中，即改变喷头温度时造成的影响更大，而Ⅰ型试样具有更大的侧边散热面积。最优填充速度曲线的变化趋势与Ⅰ型试样类似，尺寸精度预测曲线则不太相同，这是由两种试样的尺寸规格和形状差异造成的。

表4 Ⅱ型试样的v-t方差分析结果Table 4 v-t ANOVA results of Sample Ⅱ

表5 Ⅱ型试样v-T方差分析结果Table 5 v-T ANOVA results of Sample Ⅱ

2.2 填充速度与分层厚度、喷头温度的三元耦合控制函数

采用Matlab软件进行多元非线性回归分析，将式(3)和(5)整合成一个Ⅰ型试样填充速度与分层厚度、喷头温度的三元耦合控制函数关系式(11)，标准差为20.435 8：

v=41.581 6+1 147.7t-2.190 9T-2 619.3t2+0.008 0T2

(11)

同理，对于Ⅱ型试样，将式(7)和(9)整合得到填充速度与分层厚度、喷头温度的三元耦合控制函数关系式(12)，标准差为15.249 0：

v=-3 221.7+723.862 4t+30.779 6T-

1 309.7t2-0.074 1T2

(12)

式(11)和(12)对应的曲面如图4(a)和4(b)所示。

由图4可知，两种试样的填充速度与分层厚度、喷头温度的三元耦合控制函数不尽相同，在t=0.2 mm处以及T=200 ℃处的剖面图与双变量实验得到的结果接近，一定程度上也证明了该曲面的有效性。同时可知：不同的试样长宽比会影响对填充速度的控制效果，这种影响具体需要微观分析以及通过设计其他尺寸规格、形状的试样来进一步说明，如分析不同规格试样在同一组参数下的挤出线

图4 两种试样的填充速度与分层厚度、喷头温度的三元耦合作用

的微观形状、设计更多不同长宽比的试样等。限于篇幅，将在后续实验中另行研究。文中结果表明，试样长宽比、尺寸规格等在速度的控制中起重要作用，可通过调控填充速度来实现试样成型精度的改善和稳定控制。

为了检验以上构建的填充速度与分层厚度、喷头温度三元耦合控制函数的作用效果，抽取部分t和T值的组合，把根据式(11)、(12)及图4(a)、4(b)曲面计算得到的v作为成型过程的输入值进行实验，并对打印试样进行检测，获得如表6所示的尺寸偏差数据，所有抽样实验均重复3次并取均值。结果表明：所有Ⅰ型试样的等效尺寸偏差均由原来的0.22～0.44 mm全部控制在了0.3 mm以内(绝大多数不高于0.27 mm)；所有Ⅱ型试样的等效尺寸偏差由原来的0.11～0.56 mm全部控制在了0.3 mm以内(绝大多数不高于0.23 mm)。这说明，根据填充速度与分层厚度、喷头温度三元耦合控制函数得到的打印试样的成型精度得到了有效改善和稳定控制。

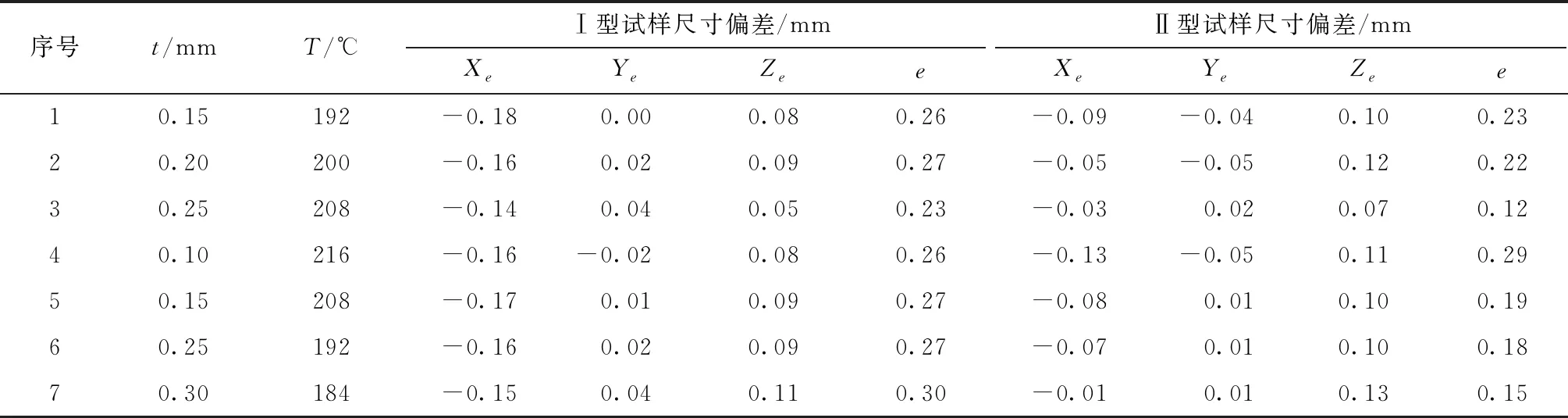
表6 填充速度与分层厚度、喷头温度三元耦合作用控制的实验结果Table 6 Experimental results obtained by ternary coupling control among filling velocity,layer thickness and nozzle temperature

3 结语

通过对PLA材料两种类型试样的双变量实验及方差分析、多元线性回归分析可知，填充速度与分层厚度、喷头温度存在的相互耦合作用影响了FDM制件的成型精度。文中主要研究结论包括3点。

(1)Ⅰ型、Ⅱ型试样中填充速度和分层厚度对尺寸精度的影响显著，同时两者交互作用的影响也显著；喷头温度对Ⅰ型试样尺寸精度的影响不显著，但对Ⅱ型试样尺寸精度影响显著，两种试样中喷头温度与填充速度交互作用的影响明显。这说明，协同控制填充速度与分层厚度、喷头温度对提高FDM制件的成型精度是很有必要的。

(2)制件的不同尺寸规格和形状会引起X、Y、Z各方向尺寸偏差占比的差异，进而影响填充速度与分层厚度、喷头温度三元耦合控制函数的构建，这种影响需要进一步实验证明，以得出适用性更广的填充速度综合控制方程。

(3)抽样打印实验结果表明，采用填充速度与分层厚度、喷头温度三元耦合控制方式制得的FDM制件，其尺寸精度可得到有效改善和稳定控制。

后续研究中，计划设计更多不同的试样进行微观分析，量化模型形状特征，由此推导出完整的、适用面更广的填充速度控制方程；同时，将进一步考虑填充速度、分层厚度、喷头温度对PLA材料性质的影响，如挤出线拉伸作用、热收缩性、离模膨胀和线宽效应等。