基于刻度准确定位的指针式仪表示数识别方法
向友君 江文 阮荣钜
(华南理工大学 电子与信息学院,广东 广州 510640)
在电网运维巡检中,以人工巡检、手动抄表、人工记录模式对变压器的油位进行检定,存在耗时耗力、自动化程度低以及误差率高等问题。随着机器人技术的快速发展,巡检机器人可代替人工,通过摄像机或红外热像仪抓取设备图像,最终对获取的图像进行处理[1- 2]。
虽然数字式仪表的应用已相当成熟,但考虑到电磁干扰、油污、灰尘等环境因素的影响,变电站等工业环境中并不适宜使用数字式仪表。指针式仪表具有抗电磁干扰能力强、精度高、价格低等优点,在相当长的时间内依然是工业生产中的主要测量仪表。由于指针式仪表无法输出数字信号,所以读数只能通过人工读取,具有工作量大、效率低、出错率高的缺点,而且安装在高温高压等环境中的仪表不便观察[3- 4]。随着国家电网对无人值守变电站的推广,实现指针式仪表示数识别的自动化得到了广泛关注。
光照变化、仪表反射、拍摄角度、表盘自身信息干扰等问题一直影响着指针式仪表的读数精度,国内外学者针对指针式仪表读数的计算进行了大量的研究。张文杰等[5]针对光照变化影响指针式仪表读数的问题,提出了一种基于视觉显著性区域检测先验知识来获得指针区域的方法,再通过旋转仪表对比指针投影最大值,获取指针与横轴的夹角,计算仪表读数。Zhang等[6]将仪表盘中每一个包含数字的刻度区间通过梯度金字塔算法单独分割并编号,用支持向量机训练分类,识别出图片中最接近指针的类别,通过三点成一直线理论消除了因表盘微小差异而引起的误差,得到了较高的准确率。Kim等[7]提出了基于形态学的处理方法,但过程较为繁琐,难以实际运用于工业生产中。李巍等[8]通过一种以图像金字塔方法来提取仪表图像特征,并以线性支持向量机来分类的预处理方法,减小了阴影因素的影响,从而提高了读数的精确度。
相较于矩形表盘,圆形表盘的示数识别难度较大,并且拍摄角度一直是影响指针式仪表读数精度的重要因素,所以文中重点研究拍摄偏角过大情况下的圆形油位计圆形表盘。目前,大多数的油位计示数识别方法还是基于表盘拍摄角度较为正面的情况,如图1(a)所示。油位计图像中包含的信息量很大,有表框、刻度、指针、文字标识,部分仪表的外框上还有一些固定物件,相当多的信息并不是读数的关键信息。事实上,如果油位计拍摄角度倾斜较大,如图1(b)所示,此时表盘形变为近似的椭圆,刻度与刻度之间的间隔也不再统一,会对读数的计算产生很大影响。有鉴于此,文中提出一种基于刻度准确定位的仪表示数识别方法,该方法无需预先添加任何表盘信息,通过粗识别与细识别精确定位出刻度的位置,将拟合刻度的圆心到指针直线的投影点作为计算用圆心,克服了传统仪表示数识别方法在倾斜角较大时仍然使用指针中心线必过仪表转动轴心的约束条件的误区,从而优化了拍摄倾角较大时的指针定位问题,进一步减小了后续计算的误差,整个过程仅使用刻度与指针这两个必要特征来计算表盘读数。

图1 油位计图片Fig.1 Photos of oil-level meters
1 仪表示数识别流程
基于刻度准确定位的指针式仪表示数识别方法包括预处理、指针检测、刻度定位、油位计表盘中心拟合与仪表读数计算5个部分。该方法无需预先添加任何表盘信息,算法流程如图2所示。整个流程分为两步且同时进行——第1步,将油位计图像进行灰度化和边缘检测等预处理,再通过指针检测获得油位计的指针信息,其中指针检测又包括概率霍夫变换检测和指针位置的计算;第2步,将原图进行灰度化、二值化和膨胀腐蚀等预处理,再经过刻度定位(刻度定位包括粗识别和细识别),使得预处理后的图像先经过粗识别粗略定位出所有可能包含油位计刻度的区域,再单独截取出粗识别的结果并进行细识别,定位出刻度,获得计算所需要的圆心信息和刻度信息,最终结合这两步计算出读数。
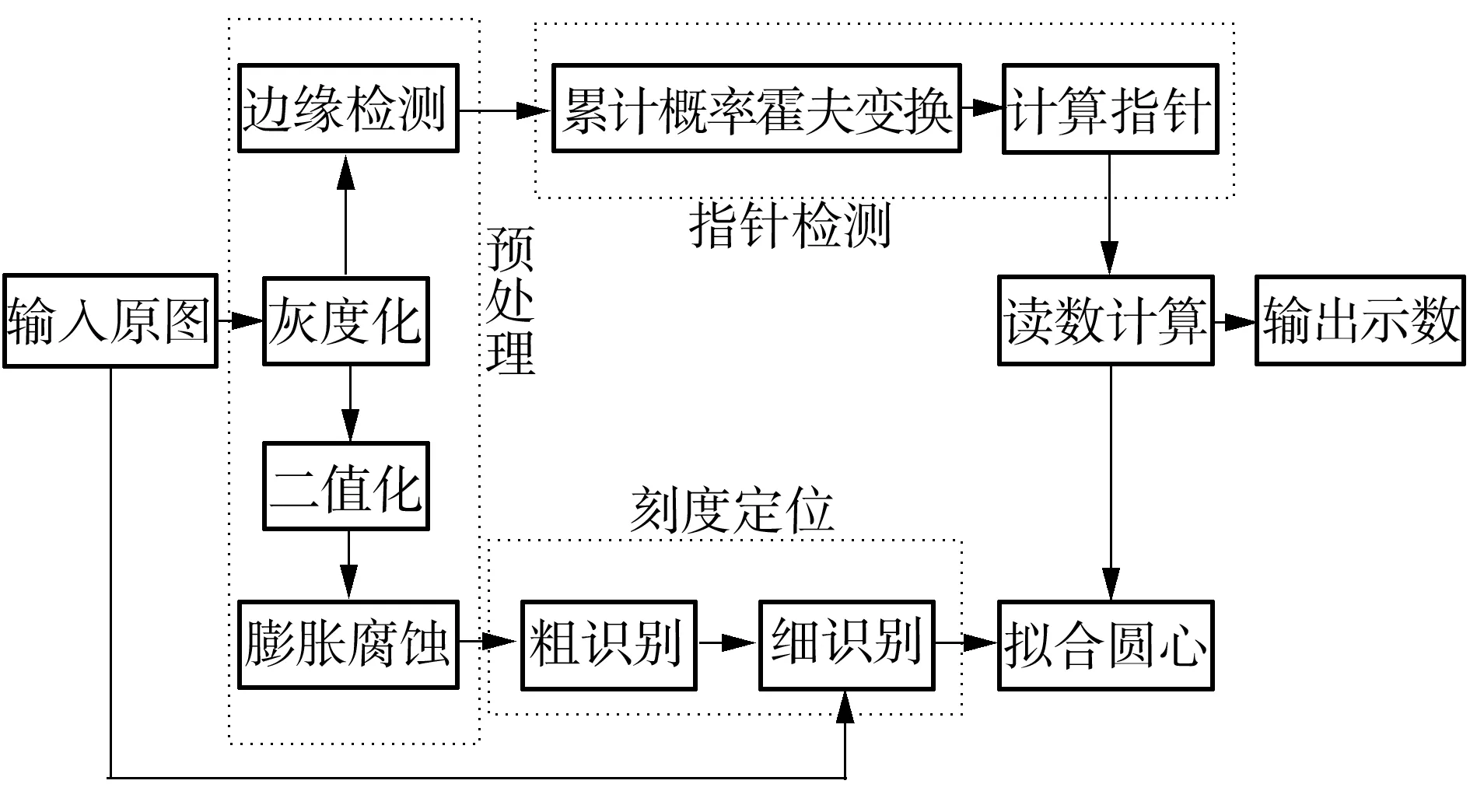
图2 文中算法流程Fig.2 Flow chart of the proposed algorithm
2 预处理
在用无人巡检机拍摄油位计图片时,由于表盘自身信息干扰或光照变化等因素的影响,无法准确提取出有用的仪表信息,从而会影响仪表读数的计算。因此,在提取指针区域之前必须对图像进行预处理以去除部分噪声,为后续指针识别和刻度定位信息的精确提取提供清晰的图像,以获得精度更高的指针式仪表读数。
2.1 二值化
指针式仪表通常暴露在室外,再加上工业生产中的光线变化及油位计自身表框或周围仪器的遮挡产生的阴影,巡检机器人采集到的图像很可能是部分阴影、部分光亮的表盘图片。为了后续精确定位刻度和提高计算效率,需要对彩色的油位计图像进行二值化处理,去除对提取表针有干涉影响的背景。图像的二值化处理就是把图像中的像素按照给定的阈值分化成黑白两种颜色。二值化处理后的油位计如图3所示。

图3 油位计的二值图Fig.3 Binary image of oil-level meter
2.2 膨胀腐蚀
为消除表盘噪声点和非实心区域,同时尽量避免对表盘内部的实心刻度与指针信息造成影响,文中采用形态学处理中的膨胀和腐蚀操作对二值化表盘图像进行预处理,具体步骤如下:首先对二值化图像的白像素进行膨胀,消除孤立噪声点和非黑的实心图像区域;然后对膨胀后的图像进行腐蚀,将被压缩的黑色部分近似恢复到原来的大小,还原表盘有效信息。膨胀腐蚀效果如图4所示。

图4 二值图膨胀腐蚀后的效果Fig.4 A binary picture going through expansion and corrosion
2.3 边缘检测
为了后续表盘指针的精确识别,需先将表盘图像转化为灰度图后再进行边缘检测。目前较为主流的边缘检测算子主要有Canny算子[9]、Laplace算子[10]、Roberts算子[11]、Sobel算子[12]等。而在所有的边缘检测算法中,Canny边缘检测[13]不但定义严格,还具有实现过程简单、检测可靠性高等优点,因此文中选择Canny检测算法来进行油位计图像的边缘检测,结果如图5所示。相比于其他3种边缘检测算法,Canny算法的检测结果更加连续,保留了原图中更多的细节,更适合后续处理中所用的方法。

图5 4种不同算子得到的油位计边缘检测结果
3 指针检测与刻度定位
通常指针直线检测都是采用霍夫变换进行的,然后直接选择矩形刻度的几何中心来计算表盘读数。在拍摄角度倾斜过大的情况下,矩形宽刻度将会被部分遮挡,使得刻度大小不一,且直接选择矩形刻度的几何中心计算刻度时会产生较大的误差,所以文中先用矩形刻度的几何中心拟合出一个粗略的圆心,然后选择每个刻度距粗略圆心较近的两个角点的中点来计算油位计读数,同时对该粗略圆心进行修正。
3.1 指针检测
霍夫变换[14- 16]一直是直线检测中比较流行的方法,其通过两个坐标空间之间的变换,将图像中直线上的所有点都在变换空间的某个点上形成峰值。但是传统的霍夫变换无法检测出油位计指针的方向。文中采用累计概率霍夫变换(Progressive Probabilistic Hough Transform,PPHT)[17]来提取指针。累计概率霍夫变换算法是标准霍夫变换算法的一个改进,它在一定的范围内进行霍夫变换,算出独立线段的范围和方向,可以实质性地减少计算时间,运行效率很高。由于油位表的指针较粗,将检测出两条线段,并且累计概率霍夫变换检测出的结果是一条直线上的两个点,这两条直线的交点即为指针针尖,指针的指向即为从圆心到针尖的方向。文中采取斜率为这两条直线斜率的平均值且穿过针尖的直线作为该油位计指针。累计概率霍夫变换检测是在油位计边缘检测的图上进行的,但是为了更显著地显示出累计概率霍夫变换的结果,文中将检测结果显示在原仪表图上,如图6所示。图6中共有4个点,这4个点即为指针累计概率霍夫变换检测的两侧直线的结果,图中所示的直线是穿过指针两侧直线交点且斜率为指针两侧直线斜率的平均值的直线,可认为这条直线是油位计指针所在的直线。

图6 油位计的累计概率霍夫变换检测结果Fig.6 PPHT detection result of for oil-level meter
3.2 刻度粗识别与精准定位
在识别倾斜角过大情况下获得的油位计读数时,由于表盘内部信息(数字、符号、仪表编号、生产厂商等)的干扰,且矩形刻度并非水平,自身的旋转角度各不相同,使用传统方法在整个油位计表盘的图像中直接定位出油位计刻度位置较为困难。为此,文中提出一个先粗识别再精确识别并定位出刻度的方法,在识别倾斜角过大情况下获得的油位计示数时,也能准确地定位出油位计刻度的位置,并提取出刻度中更有利于抗角度干扰的后续计算读数所需的信息。
首先对油位计刻度进行粗识别,在膨胀腐蚀结果中寻找各个闭合形状的边缘点集,判断各个闭合区域的大小,设定最大阈值和最小阈值,将面积不属于该阈值范围内的区域过滤掉,然后求出该区域的最小外接矩形,将最小外接矩形的中心坐标保存在一个列表中。粗识别的结果如图7所示。此时保留的中心坐标包括了刻度外接矩形的中心坐标和一些干扰信息的中心坐标。为了去除这些干扰信息,以粗识别获得的最小外接矩形中心继续作为中心,略微扩大矩形框的长与宽,在对应表盘原图中截取如图8(a)所示的图片。对截取的图片使用Harris角点检测方法[18]进行矩形检测,排除掉角点过多和角点无法形成矩形的图,得到真正的刻度。Harris角点检测结果如图8(b)所示。所得矩形刻度4个角点中,距离圆心较近的两个角点所对应线段的中点用于后续油位计读数的计算。

图7 油位计粗识别结果Fig.7 Result of coarse recognition of oil-level meter


图8 截取的粗识别出的部分图片及其Harris角点检测结果
3.3 油位计表盘中心的拟合
在精确定位刻度之后,先用所有矩形刻度的几何中心拟合出一个粗略的圆心,获取每个矩形刻度的4个角点与该圆心的距离,距圆心最短的两个角点的连线中点构成一组坐标点。这组坐标有一个共同点,即该组坐标全部近似位于一个椭圆上,满足以下关系:
x2+Axy+By2+Cx+Dy+E=0
(1)
式中,A、B、C、D、E为椭圆的未知参数。通过最小二乘法对该组坐标进行拟合,得到目标椭圆,因此可设置目标函数F如下:
Cxi+Dyi+E)2
(2)
由于有A、B、C、D、E共5个未知数,所以要求的采样点至少为5个,式中N为采样点个数。
要使目标函数F最小,即需
(3)
可得圆心方程为
(4)
设满足上述目标函数的目标椭圆圆心为(xc,yc)。拟合的结果如图9所示。

图9 拟合的圆心Fig.9 Fitted center
在拍摄倾角过大时,拟合得到的椭圆圆心与指针并不在一条直线上,若将其直接用于计算读数,获取的油位计读数误差会较大。因此,选择圆心(xc,yc)距累计概率霍夫检测得到的指针直线方程上最近的一点作为真正用于计算的圆心(xt,yt)。
4 读数计算
传统方法[19]计算指针式仪表的读数时,一般通过Hough变换直线检测来获取正面圆盘图像的指针角度信息,在获得直线的角度后,即可计算出读数。假设:直线的角度为θ;最小刻度为kmin,对应的角度为θmin;最大刻度为kmax,对应的角度为θmax;读数用k表示。那么,k可由以下公式计算:
(5)
但是,在拍摄角度倾斜较大的情况下,每两个相邻的刻度与圆心组成的夹角不是一个完全相等的值,也就是说,采集图像中的指针与刻度线的角度差有的偏小有的偏大。这将导致指针相对于每个刻度线的读数出现误差。对于传统方法,可以使用透视变换来对油位计的图片先进行校正。透视变换是将图片投影到一个新的视平面,拥有较高的灵活性。结合油位计的先验信息(起始刻度倾角与末位刻度倾角),即可用传统的方法计算出油位计的读数。但该方法需要预先选取4个点,而油位计表盘没有合适的参考点,因此需要手动选出4个点来校正表盘。而文中提出的油位计示数识别方法,无需对表盘进行校正也能准确地计算出读数。
文中读数计算方法的步骤如下:
步骤1 计算所有矩形刻度精确定位后所得坐标点与相邻两个坐标点的距离并求和;
步骤2 根据油位计表盘信息可得:距离和最大的两个点为0与10,且巡检机器人拍得的图片中0的纵坐标大于10的纵坐标,即可求得0与10坐标;
步骤3 接着计算与0距离最近的点,即为1,依次可将所有坐标点对应的数字一一求出;
步骤4 计算所有坐标点与指针针尖的距离,距离针尖最近的两个坐标点记为k1与k2(k1+1=k2);
步骤5 使用式(6)计算表盘读数k:
(6)
式中,d1、d2分别为k1、k2到指针所在直线的距离,s1、s2分别为k1、k2与计算用圆心(xt,yt)的距离。参数位置如图10所示。
5 实验结果分析
在Window 10(处理器为Intel(R)Core(TM)i5-8500 CPU 3.00 GHz,内存16 GB)系统下使用Python作为开发环境并对油位计图像进行处理。为了检测算法的适用性和稳定性,文中实验采用了不同仪表示数、不同光照条件、不同天气环境下拍摄的倾斜角较大的指针式仪表图像样本共50幅,通过文中的仪表示数识别方法对指针式油位计示数进行识别,总误差率为0.92%。图11所示为其中10幅样本,表1为该10幅样本对应的真实值和采用3种方法分别得到的测试结果。由表1可知:传统的角度计算方法在处理拍摄倾角较大的图像的时候,误差率高达8.55%;经过透视变换后,传统方法的误差率降低了5.26个百分点;文中方法所得结果与真实值的误差率为0.86%。3个识别方法中,透视变换校正表盘的方法忽略了手动选取参考点的时间,因此,从表1可看出,文中算法虽然增加了一些复杂度,但仍然可以满足实际工程应用中的需求。

图11 10幅样本表盘Fig.11 10 sample oil-level meters

表1 指针式油位表示数识别的实验结果
6 结论
针对拍摄角度较大时传统仪表示数识别方法计算精度较低的问题,文中提出了一种可以精确定位出刻度并识别对应刻度的、基于刻度准确定位的仪表示数识别方法。该方法不需要在识别示数前预先提取指针区域和定位指针中心线,仅使用刻度与指针这两个必要信息特征来实现表盘读数的计算。通过累计概率霍夫变换,既能检测出更能代表指针的平均斜率直线,也能判断出指针的指向。采用角点检测后的近圆心坐标点作为计算用坐标点,解决了刻度被部分遮挡情况下对整个油位计刻度定位难的问题。采用拟合圆心到指针直线的投影点作为计算用圆心,克服了传统仪表示数识别方法在倾斜角较大时仍然使用指针中心线必过仪表转动轴心的约束条件的误区。实验结果表明,该方法获得的仪表读数精度平均达到99.08%,较其他传统算法更加稳定可靠。
在极端拍摄倾角下,有些刻度将被彻底遮挡,这会对指针式仪表读数产生很大的影响。在下一步研究中,将结合数字识别,研究极端拍摄倾角下刻度丢失时的仪表读数计算问题,并将探索在水雾、雨滴、灰尘等遮挡所引起的表盘图像模糊情况下的仪表自动读数问题。

