基于实时阴影技术的混凝土箱梁竖向温度梯度模式

盛兴旺 郑严煌 郑纬奇† 朱志辉,2

(1.中南大学 土木工程学院，湖南 长沙 410075；2.高速铁路建造技术国家工程实验室，湖南 长沙 410075)

由于混凝土导热系数较小，在太阳辐射作用下，混凝土结构内部的温度变化会明显滞后于表面的温度变化[1]，从而形成较大的温度梯度。当由温度梯度产生的温度变形受到箱梁自身或多余约束制约时会产生温度应力，有时甚至比汽车荷载产生的应力还要大，很多混凝土桥梁因此发生严重裂损。

目前已有诸多学者从不同角度对混凝土箱梁的温度梯度模式进行了研究。肖新辉等[2]基于对四川腊八斤特大桥箱梁温度场的连续观测，提出了四川雅安地区的混凝土箱梁温度梯度计算模式。刘广龙等[3]以新疆小沙河中桥为背景，通过试验实测与有限元分析，研究了西北极寒地区混凝土箱梁温度场的特点及温度效应。Hossain等[4]实测了美国路易斯安那州John-James-Audubon大桥的温度分布，发现大桥的温度梯度与美国公路桥梁标准规范吻合较好。Lawson等[5]依据美国内华达州的气象资料，采用热流分析法分析了美国西南部沙漠气候中典型混凝土箱梁的温度梯度。以上研究所得到的温度梯度计算模式虽然精确度较高，但使用范围仅限于部分地区，应用上存在很大局限性。我国现行行业规范《公路桥涵设计通用规范》(JTG D60—2015)将全国各地的混凝土箱梁温度梯度取为同一模式，没有考虑地理位置和气候对温度梯度取值的影响，这种单一模式虽然易于推广，但是否适用于我国各个地区、是否足够精确和安全，还有待进一步研究。

文中基于实时阴影技术，利用ANSYS平台建立混凝土箱梁结构的有限元模型，通过热分析方法得到混凝土箱梁结构的实时温度场分布规律。根据我国气候地域分布特征，选择典型地域来代表我国各类气候特征，基于以上方法得到各个典型区域的温度场分布，对其竖向温度梯度分布规律和模式进行分析，从中选取不利值，将其与国内外常用竖向温度梯度模式进行对比研究，以期为我国混凝土箱梁结构的温度梯度取值提供一些有益参考。

1 日照温度热量计算及实时阴影面

混凝土结构与外界无时无刻不在进行热交换，热交换形式一般分为短波辐射、长波辐射以及对流换热，如图1所示。结构物根据其结构特征、地理位置和太阳方位，可分为结构光照面和阴影面，结构物的光照面、阴影面与外界发生的热交换不尽相同，且光照面和阴影面相互转换，时时变化。结构物的实时阴影面可以通过实时阴影技术计算，它决定了不同时刻箱梁各部位受到的有效辐射类型，从而影响温度场模拟计算的准确性。文中所用各类热交换计算方法和实时阴影面的选取方法如下文所述。

图1 桥梁结构的热环境Fig.1 Thermal environment of the bridge

1.1 短波辐射

短波辐射包含了太阳直接辐射、太阳散射辐射、地面对太阳直接辐射和散射辐射的反射。太阳直接辐射量Iθ表示为[6]

(1)

式中，P、h、I0、θ分别为大气透明度、太阳高度角、地球外缘的太阳辐射强度、太阳入射角。

太阳高度角按下式计算：

h=arcsin (cosφcosδcosω+sinωsinδ)

(2)

φ、ω、δ分别为桥梁所在位置的纬度、时角和赤纬角。

时角ω在不考虑时差的情况下可表示为

(3)

由于地日距离随地球公转而变化，所以I0不是一个定值，可按下式计算[7]：

(4)

式中，D为从该年1月1日起的日序数。

太阳散射辐射量Id与结构物表面方位角无关，只与表面倾角有关。在晴天无云情况下Id为

(5)

1.2 长波辐射

混凝土箱梁结构不断地向周围环境发出辐射热，同时吸收周围其他物体发出的辐射热[8]。长波进入混凝土箱梁的热流密度qr为

qr=Al(Gaβ+Uaβ)-El

(6)

式中，Al为长波辐射吸收率，Gaβ、Uaβ分别为混凝土箱梁吸收的大气长波热辐射和地表长波热辐射，El为混凝土箱梁向外界辐射的能量。

对于倾角为β的箱梁表面，其吸收的大气长波热辐射Gaβ和地表长波热辐射Uaβ可分别用下式计算：

(7)

(8)

式中εa、C0、TA分别为大气辐射系数、斯蒂芬-玻尔兹曼常数、大气温度。大气温度的日变化过程可以根据日最高、最低温出现的时刻和大小，采用正弦函数描述。

对于土木工程结构，表面热辐射能El可采用斯蒂芬-玻尔兹曼定律经验修正公式进行计算[9]：

El=εBC0(273+TB)4

(9)

式中，εB为混凝土表面辐射发射率，TB为箱梁表面温度。

1.3 对流换热

混凝土表面与外界的对流换热遵循牛顿冷却定律[10]，即

qc=hc(TB-TA)

(10)

式中，hc为对流换热系数，当风速v小于5 m/s时可根据凯尔别克提出的经验公式进行计算：

(11)

1.4 实时阴影面

箱梁腹板受翼缘遮挡而产生的阴影会改变其热环境，增大腹板与顶板间的温差，从而影响箱梁竖向温度梯度的模式与数值。因此，为了得到更加可靠的箱梁竖向温度梯度，必须准确计算实时阴影面。实时阴影面的计算基于实时阴影技术，这是一种通过光线追踪来判断阴影区域的计算机图形学算法[11- 13]。对箱梁边腹板的实时阴影面求解时需要考虑腹板自身形成的自阴影区域，以及其余结构物对腹板形成的他阴影区域两个部分。

对于自阴影区域，可以通过太阳光线向量与腹板外表面法向向量的夹角μ来判断，当μ小于等于90°时，认为光线被腹板内侧遮挡，无法直射腹板外侧。图2所示梁体的整个右腹板外侧均为光束1作用下的自阴影区域。

他阴影区域的求解分两步进行。第1步：求出光线与悬臂板底部4个角点所在平面A的交点J的坐标。第2步：判断J点是否落在悬臂板下部4个角点所围成的面域a内，如果落在面域a内，就意味着光线被悬臂板遮挡，无法直射腹板，反之则未被遮挡。

J点的坐标可以通过腹板单元表面中心点W的坐标以及太阳高度角、太阳方位角求得。点W的坐标可通过单元节点坐标得到。假设桥梁为南北走向，并以横桥向为X轴，梁高方向为Y轴，顺桥向为Z轴，则中心点W与交点J存在如下关系：

JX=cosh×sinα×d+WX

(12)

JZ=cosh×cosα×d+WZ

(13)

d=(H-WY)/sinh

(14)

式中,WX、WY、WZ分别为中心点W的X、Y、Z坐标,JX、JZ分别为交点J的X、Z坐标,α为太阳方位角,d为点J与点W的距离,H为悬臂板下部至梁底的距离。

求得点J的坐标后，需要判断J是否落在面域a内。假设悬臂板下部4个角点按顺序排列为N1、N2、N3、N4，令向量Vi=Ni-J(i=1,2,3,4)，V5=V1。如果叉积Vi×Vi+1(i=1,2,3,4)符号相同，则交点J落在面域a内。对各时刻腹板外表面单元进行求解，即可得到考虑了他阴影区域的实时阴影面。

由以上分析可知，实时阴影面与光束入射的角度息息相关，而光束入射角度受桥址影响，因此经纬度不同的箱梁阴影面存在差异，内部温度场也不尽相同。

2 有限元模型与计算参数

2.1 模型的建立

利用ANSYS建立3×30 m简支箱梁桥模型，单元种类为solid70。主梁的截面形式如图3所示，模型如图4所示。

图3 主梁截面尺寸Fig.3 Size of main girder section

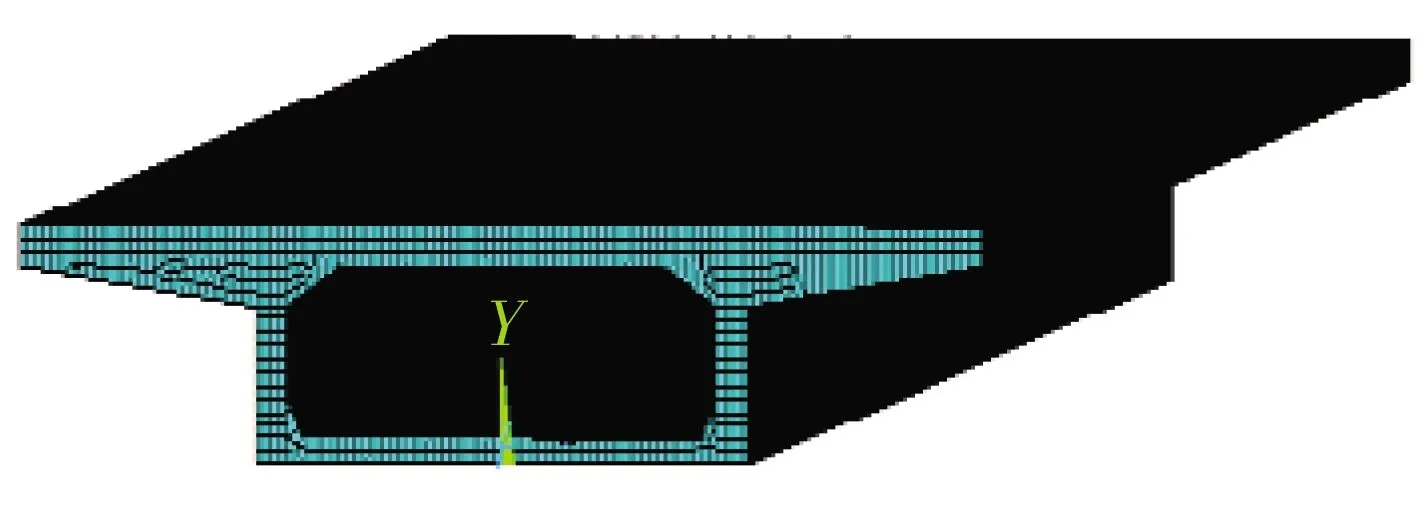
图4 有限元模型Fig.4 Finite element model

为求解箱梁的温度，首先需要求出箱梁单元与外界环境的热交换量。在3种热交换量中，短波辐射量由时间和单元位置决定，长波辐射量、对流辐射量由时间和单元表面温度决定，而单元表面温度正是需要求解的。为了解决这个问题，编程时先假定一个温度范围，该范围囊括了箱梁可能出现的温度，在每个时间步对各单元求取单元表面温度处于假定温度范围内时的长波辐射量、对流辐射量，再与对应的短波辐射量叠加，从而建立可以通过单元位置、时间、单元表面温度检索的热流密度表格，并以此为荷载边界条件进行计算。由于混凝土结构的温度与时间存在较大关联性，为减少初始温度场的影响，在计算过程中需进行多次迭代，迭代多次后计算结果逐渐稳定[14]。文中的迭代次数为7次。

2.2 计算参数

在运用传热学进行温度场计算时，需要确定太阳辐射吸收率、辐射发射率、密度、比热容、导热系数等。文中参照李彦伟等[15]的研究，拟定如表1所示的材料参数。

表1 材料的热工参数Table 1 Thermal parameters of materials

2.3 模型的验证

按照铺装类型将模型分为两类。将唐山市、延安市和上海市的计算结果与文献[9，16- 17]的实测结果进行对比，验证模型的准确性。模型的环境因素如表2所示。

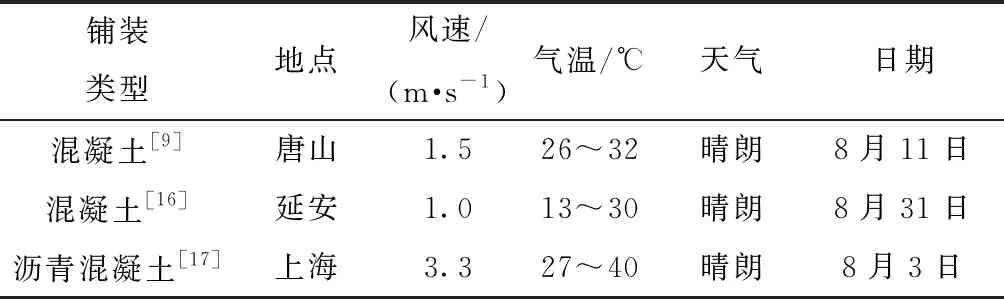
表2 模型的环境因素Table 2 Environment factors of the model

计算结果与文献[9,16- 17]中实测数据的对比如图5所示。文献中的温度实测数据与ANSYS计算值的变化趋势相同，混凝土铺装模型、沥青混凝土铺装模型实测值与计算值的平均相对误差分别为8.4%、5.1%，证明文中算法准确性较高，足以满足工程要求。

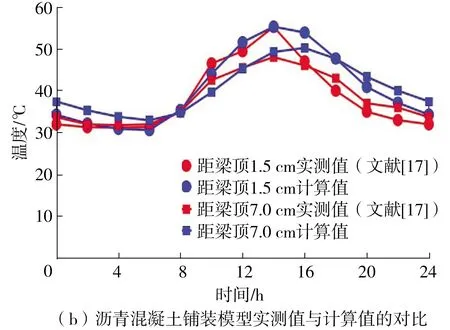
图5 两类模型实测值与计算值的对比

3 我国混凝土箱梁的温度梯度分布模式

3.1 我国典型温度地理区域划分

气候类型决定了气温的整体变化情况，因此典型温度地理区域按照典型气候类型来划分。我国的气候类型主要可分为：热带季风性气候、亚热带季风性气候、温带季风性气候、温带大陆性气候、青藏高原高寒气候[18]。

热带季风性气候分布于海南、南海诸岛；亚热带季风性气候分布于北回归线以北的南方省份；温带季风性气候分布于东北和北方省份；温带大陆性气候分布于新疆、内蒙古；青藏高原高寒气候分布于西藏、青海。各典型气候分区的温度条件、日照时长、太阳辐射强度均存在明显差异，而这些正是影响箱梁温度场的重要因素。

3.2 我国混凝土箱梁的温度梯度模式

在上文已验证模型的基础上，选取各典型气候地区中的代表性城市，考虑两种不同的铺装类型，共建立60个模型。环境因素按如下描述确定：风速取1 m/s，天气晴朗，气温按该城市最高温月份的平均最高、最低气温确定。由于沥青铺装层对温度梯度产生的微小裂缝具有良好的自恢复能力，故温度梯度均从混凝土层表面开始提取，两类模型最大温度梯度的计算结果如图6所示。

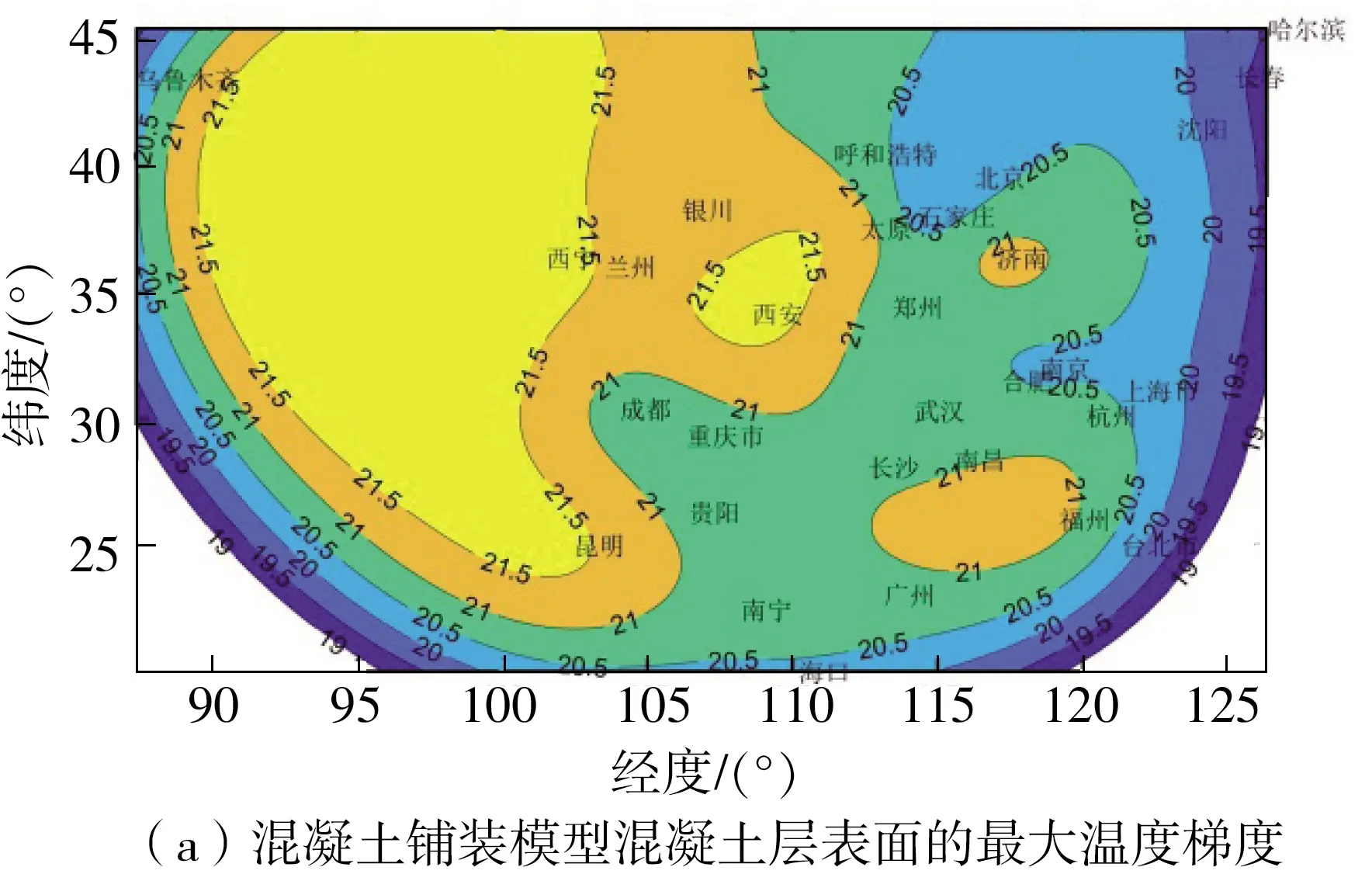
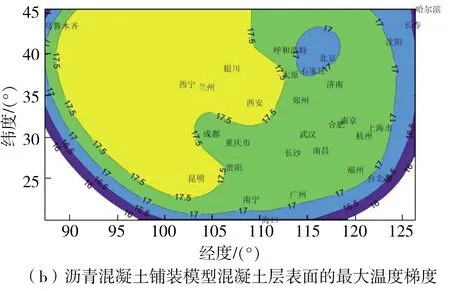
图6 混凝土层表面的最大温度梯度分布

采用混凝土铺装时最大温度梯度为19.0～21.5 ℃，采用沥青混凝土铺装时最大温度梯度为16.0～17.5 ℃。由图6可知，最大温度梯度分布受经度以及各地气候的影响。热带季风性气候、亚热带季风性气候、温带季风性气候区域的最大温度梯度相近。温带大陆性气候和青藏高原高寒气候区域的最大温度梯度较高。

绘制计算结果中混凝土层表面温度梯度最大的城市——西安的竖向温度梯度曲线，并与国内外既有规范值对比，结果如图7所示。

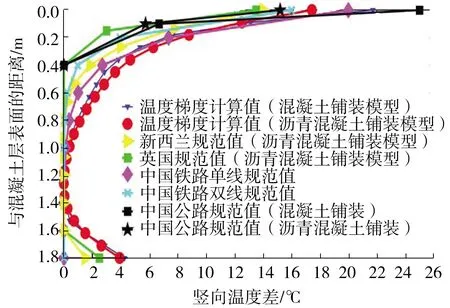
图7 温度梯度计算值与现有规范值的对比

由图7可看出，无论是数值还是曲线形式，国内外规范与西安地区的计算结果均有所不同。

在数值上，西安地区的混凝土铺装模型、沥青混凝土铺装模型的梁底最大温度梯度计算值分别为4.2和3.9 ℃，均大于各规范值。混凝土铺装模型的梁顶最大温度梯度计算值为21.7 ℃，对比图中所示各个规范值，仅小于中国公路规范中规定的25 ℃，说明中国公路规范对混凝土铺装箱梁梁顶温度梯度的设定值比实际情况大。沥青混凝土铺装模型的梁顶最大温度梯度计算值为17.4 ℃，大于包括中国公路规范在内的大多数国内外规范的设定值，说明中国公路规范对沥青混凝土铺装箱梁梁顶温度梯度的设定值比实际情况小。

在曲线形式上，中国公路规范规定的温度梯度集中分布于距离梁顶0.4 m的范围内，且未考虑梁底温度梯度；而计算所得的温度梯度曲线不仅广泛分布于距离梁顶1 m的范围内，梁底也存在明显的温度梯度。

为解决上述问题，将计算所得温度梯度曲线分为上下两段重新进行拟合。对比各国规范发现，计算所得温度梯度曲线上段与中国铁路规范规定的温度梯度曲线形式相近，故参照中国铁路规范采用指数函数拟合，结果如下：

T=21e-5.5x, 混凝土铺装

(15)

T=17e-3.5x, 沥青混凝土铺装

(16)

式中，T为箱梁边腹板中轴线处混凝土温度(℃)，x为计算点与混凝土层顶面的距离(m)。

两类模型的温度梯度曲线下段基本重合，且与新西兰规范的形式相近，故参照新西兰规范采用同一条直线进行拟合：取梁底温度梯度为4 ℃，距梁底0.4 m处为温度梯度零点，中间使用直线插值。

3.3 铺装层对最大温度梯度出现时间的影响

铺装层的存在不仅会改变最大温度梯度数值的分布，也会对最大温度梯度出现时间的分布产生影响。提取两类模型最大温度梯度出现时间的计算结果，如图8所示。

图8 混凝土层表面最大温度梯度出现时间的分布

混凝土铺装模型最大温度梯度的出现时间为13:00—15:00，沥青混凝土铺装模型最大温度梯度的出现时间为15:00—17:00，表明经度相近的典型气候地区混凝土层表面的最大温度梯度出现时间相近。

结合图7、9可以看出：在混凝土层表面温度梯度分布的形式上，沥青混凝土铺装模型与混凝土铺装模型基本相同；在温度梯度分布的数值上，沥青混凝土铺装模型相对混凝土铺装模型最大温度梯度上限值降低4 ℃，下限值降低3 ℃，最大温度梯度出现时间滞后2 h。这说明，沥青混凝土铺装层能降低温度梯度大小，减小各个典型气候地区间的最大温度梯度差异，延迟最大温度梯度的出现时间。

4 结论

文中采用实时阴影技术并基于ANSYS平台建立了箱梁的热力学分析模型，通过与现有文献中的温度实测结果进行对比，验证了模型算法的准确性；并以此为基础，分两种不同铺装类型，建立了60个位于各典型气候地区的主要城市的混凝土箱梁模型，经过求解分析得到以下结论。

(1)我国混凝土箱梁温度梯度最大的城市是西安，其温度梯度曲线应分为上、下两段进行拟合。上段采用指数函数拟合，下段采用直线拟合，以距梁底0.4 m处为温度梯度零点，梁底最大温度梯度取4 ℃，中间使用直线插值。

(2)现行中国公路规范在规定混凝土箱梁温度梯度模式时，正温度梯度分布范围过小，未考虑梁底负温度梯度，对混凝土铺装箱梁梁顶温度梯度取值偏大，对沥青混凝土铺装箱梁梁顶温度梯度取值偏小。

(3)温带大陆性气候和青藏高原高寒气候地区，混凝土层表面最大正温度梯度较大；经度相近的典型气候地区，混凝土层表面最大温度梯度的出现时间相同。

(4)采用混凝土铺装时，箱梁最大温度梯度为19.0～21.5 ℃，出现时间为13:00—15:00。采用9 cm厚的沥青混凝土铺装层时，箱梁最大温度梯度为16.0～17.5 ℃，出现时间为15:00—17:00。