含模糊不确定性的动力总成悬置系统固有特性分析与优化

吕辉 杨坤 黄晓婷 袁煜 李沛航

(1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.华南理工大学广州学院 汽车与交通工程学院， 广东 广州 510800)

动力总成悬置系统(Powertrain Mounting System，PMS)是汽车结构的重要组成部分。受制造工艺、测量误差和材料老化等的影响，PMS的参数在工程实际中不可避免地存在着不确定性[1]，因而很有必要开展含参数不确定性的PMS可靠性与优化设计研究。

针对PMS存在的参数不确定性，谢展[2]基于随机模型和拉丁超立方抽样对PMS进行了多目标稳健性设计；时培成等[3]基于随机模型和蒙特卡洛法提出了一种PMS的稳健性设计方法。Cai等[4]将PMS不确定参数视为区间变量，基于切比雪夫多项式和顶点法，提出了一种PMS固有特性区间响应的数值分析与优化方法；此外，Wu[5]基于区间模型对PMS的固有特性进行了区间稳健性优化。

目前关于不确定条件下的PMS设计研究主要基于随机或区间模型开展，可能还存在一些关键问题需解决。一方面，汽车结构可能还存在模糊不确定性[6]。模糊性是指客观事物差异的中间过渡中的“不分明性”。例如，在对PMS参数取值进行合理匹配时，合理与不合理之间是模糊的，二者之间并不存在绝对明确的分界线，即是不确定的。诸如此类的不确定情形难以运用现有的随机和区间方法处理。另一方面，为使不确定条件下的PMS优化设计进一步完善和系统化，很有必要探讨其他不确定情形下的PMS可靠性分析和优化设计，使得工程师能根据工程实际选择更为合适的分析方法。

模糊理论是在美国著名自动控制专家Zadeh[7]提出的模糊集合的基础上发展起来的。目前，模糊理论已在热传递分析[8]和制动尖叫[6]等工程领域中得到有效应用，但尚未应用于PMS的分析与优化设计。有鉴于此，文中开展了含模糊不确定性的PMS固有特性的可靠性分析与优化，以期为具有模糊特性的汽车PMS设计提供理论参考和工程指导。

1 PMS的固有特性

1.1 固有频率

图1给出了某横置前驱汽车的PMS动力学六自由度模型[2]。图中，G0为动力总成质心，Ei为悬置元件的弹性中心，ui、vi和wi(i=1,2,…，N为悬置个数)分别为悬置元件的主轴方向。

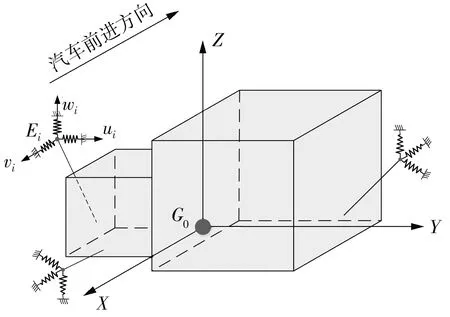
图1 PMS动力学模型Fig.1 Dynamical model of a PMS

系统振动的动力学微分方程为

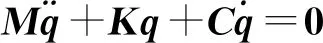
(1)

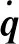
φj=[(φj)1,(φj)2,…,(φj)6]T。

1.2 解耦率

当系统以第j阶固有频率fj和振型φj振动时，第k个广义坐标占系统总能量的百分比[9]为

(2)

式中，(φj)k和(φj)l分别为φj的第k和l个分量，Mkl为质量矩阵第k行第l列的元素。

与第j阶模态对应的解耦率定义为

(3)

当dj=100%时，系统第j阶振动的能量都集中在第k个广义坐标上，该阶振动完全解耦。

2 PMS的模糊不确定性分析与优化

对于参数样本信息具有模糊特性的情形，可采用模糊变量[10]对其进行描述。

(4)

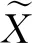
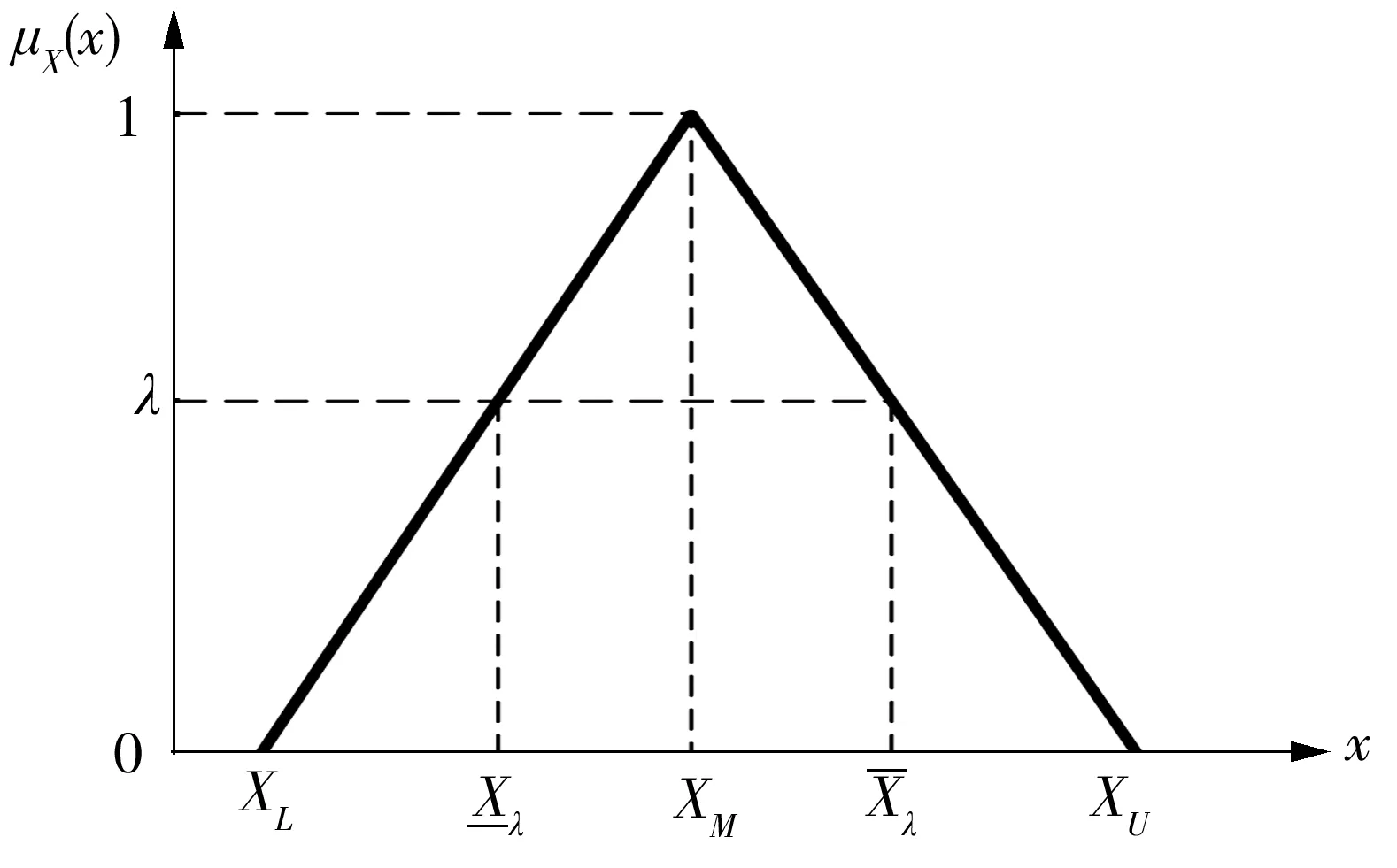
图2 三角模糊变量的隶属度函数Fig.2 Membership function of triangular fuzzy variables

(5)

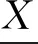
隶属度从1到0变化时，对应的水平截集取值范围在变量主值附近由小逐渐增大，反映了参数在其名义值附近逐渐发生变化的过渡状态。

(6)

(7)

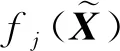
2.1 模糊-蒙特卡洛法

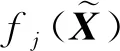
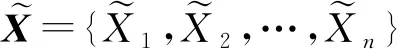
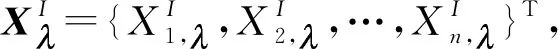
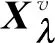
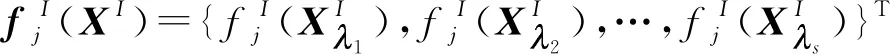
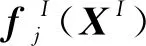
FMCM需要抽取足够多的样本数量来获得较为精确的响应结果，计算效率往往较低。因此，有必要探寻另一种相对高效的数值方法。

2.2 模糊摄动-中心差分法

(8)

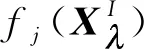
(9)

式中，ΔXp为一个趋近于0的微小增量,ΔXp=[0,…,ΔXp,…,0]T。

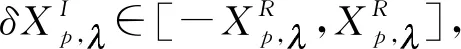
(10)

(11)

2.3 模糊可靠性分析与优化

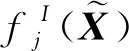
(12)

(13)

(14)

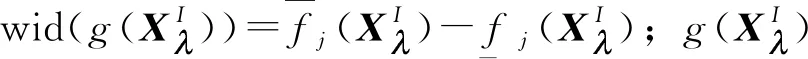
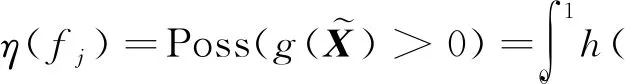
(15)

对于PMS解耦率，一般仅要求其下界大于某一值。根据式(12)、(14)和(15)，同理可得解耦率响应的模糊可靠度η(dj)。

传统的可靠性分析[8]只关注“最坏情况”，可靠度值仅为0或1。这种评价方式忽略了响应区间的过渡信息，结果过于保守。文中引入的模糊可靠性分析有效利用了区间的过渡信息，求得的可靠度可介于0和1之间。

当PMS固有特性响应不满足设计要求时，需对其进行优化。文中将优化目标设为最大化解耦率的加权值，优化约束设为固有特性的模糊可靠度不小于给定值，设计变量定义为模糊变量的主值，因此，PMS的模糊可靠性优化模型可表示为

(16)

s.t.

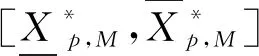
基于FMCM求解上述优化模型会出现多层嵌套，而基于FPCDM可有效避免优化嵌套，进而提高优化效率。基于FPCDM的PMS模糊可靠性优化流程如图3所示。

3 应用分析

3.1 PMS模型

文中以某四缸横置发动机三点悬置系统为例进行应用分析，且仅选取悬置刚度为研究参数。悬置初始刚度ku、kv和kw如表1所示。

3.2 PMS固有特性计算

PMS中悬置刚度参数的设计值与实测值之间的误差往往并非稳定在某个确定值[14]，而是可能处在一个过渡变化的范围。此外，由于测试数据样本有限，用随机模型描述其不确定性并不一定准确，采用区间模型描述则会完全忽略已知的部分样

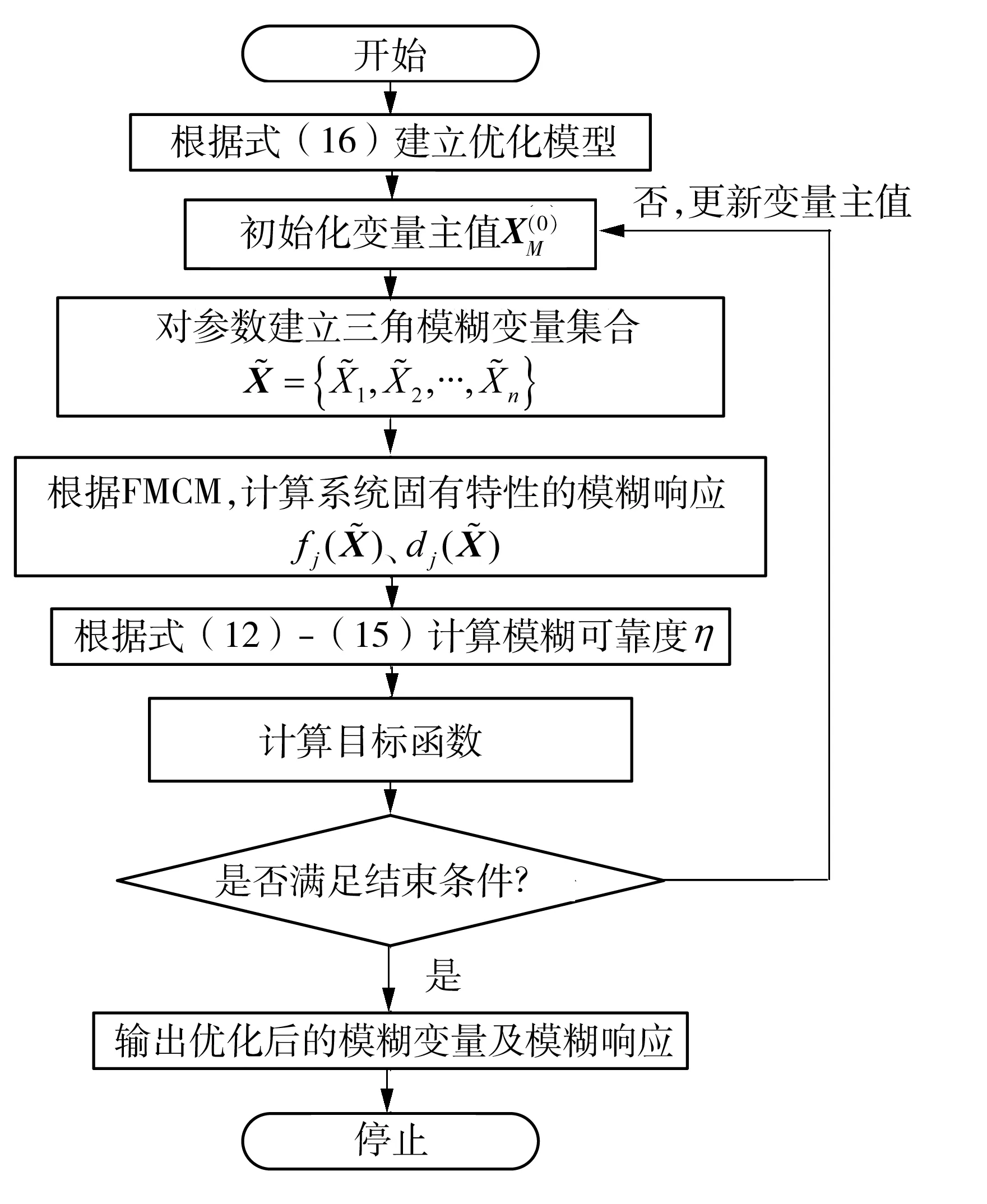
图3 PMS优化流程图Fig.3 Flow chart of optimization of PMS

表1 悬置刚度取值Table 1 Stiffness values of mounts

本信息。因此，文中将悬置刚度视为模糊变量进行研究。

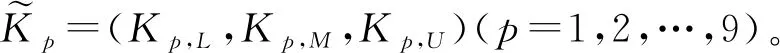
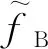
由FMCM和FPCDM求得的系统固有特性模糊响应如图4所示。

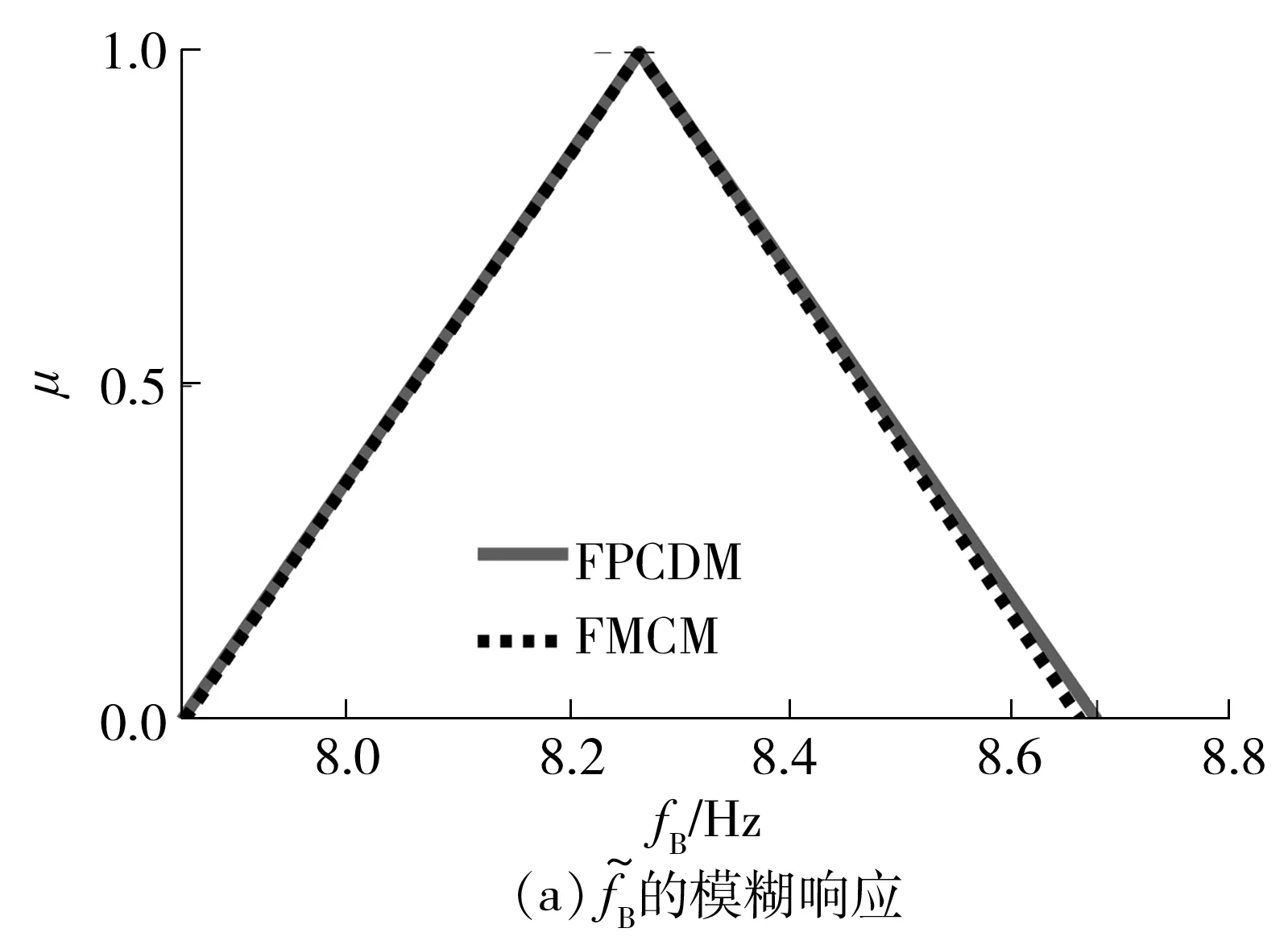
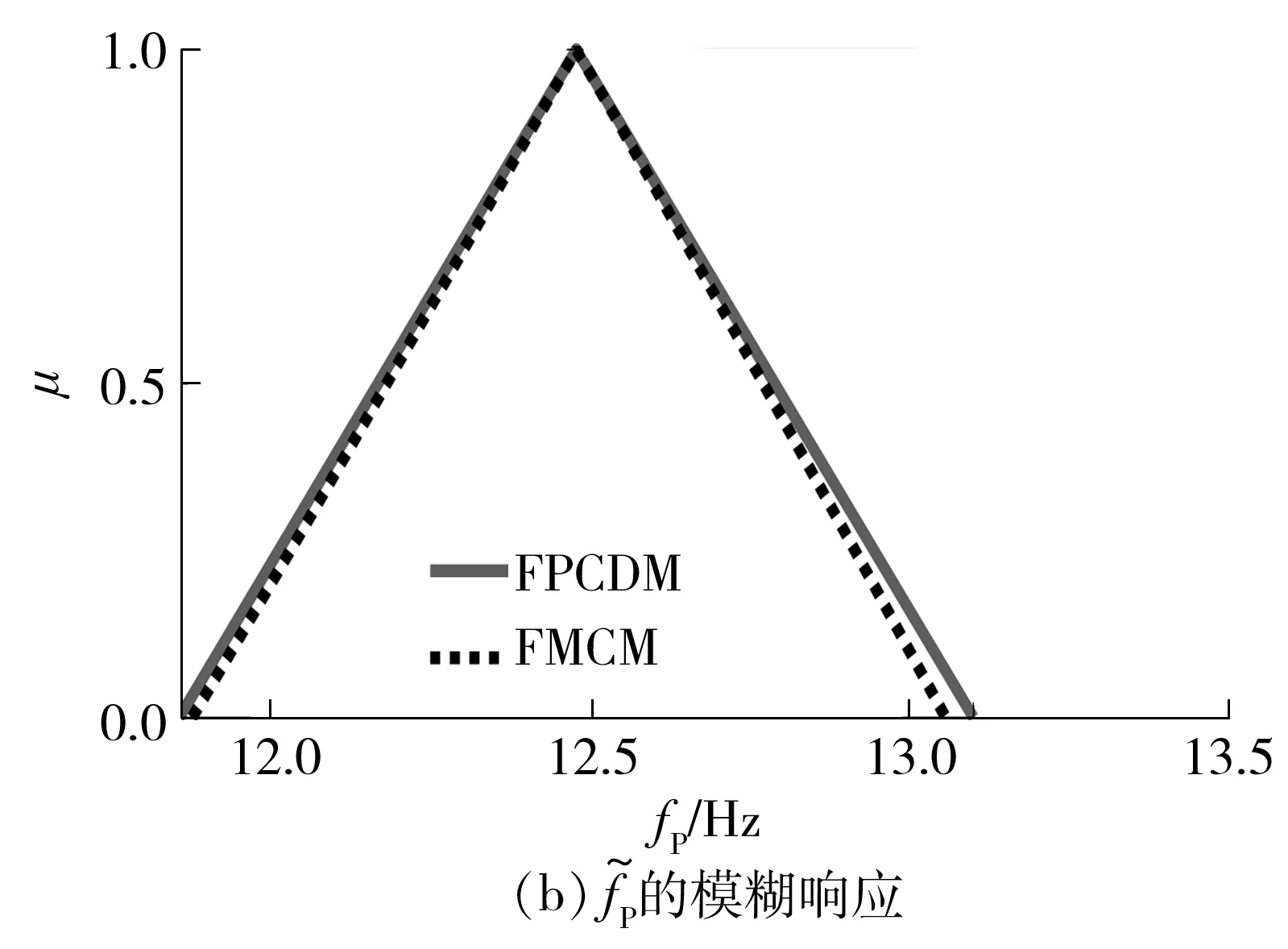
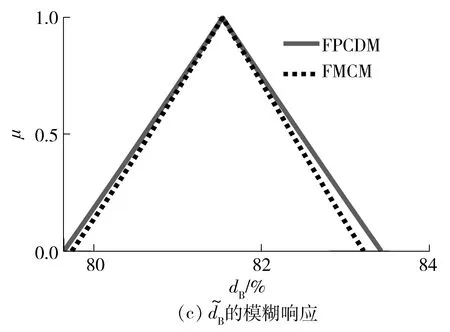
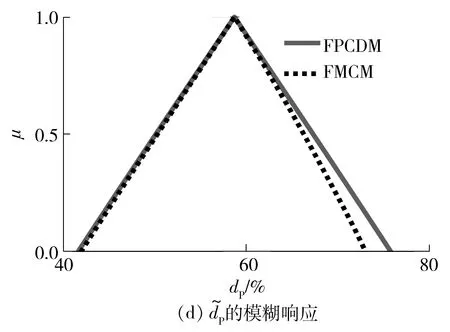
图的模糊响应

当抽样次数足够多时，蒙特卡洛法能达到非常高的计算精度，因而很多研究将其作为参考方法[15]。为了验证FPCDM计算的有效性，文中以FMCM求得的结果作为参考，用于评价FPCDM的计算精度。

FPCDM计算得到的相对误差er表示为

(17)

式中，yFMCM为FMCM求得的值，yFPCDM为FPCDM求得的值。

根据式(17)，将图4所示计算结果转化为FPCDM计算得到的相对误差曲线，如图5所示。

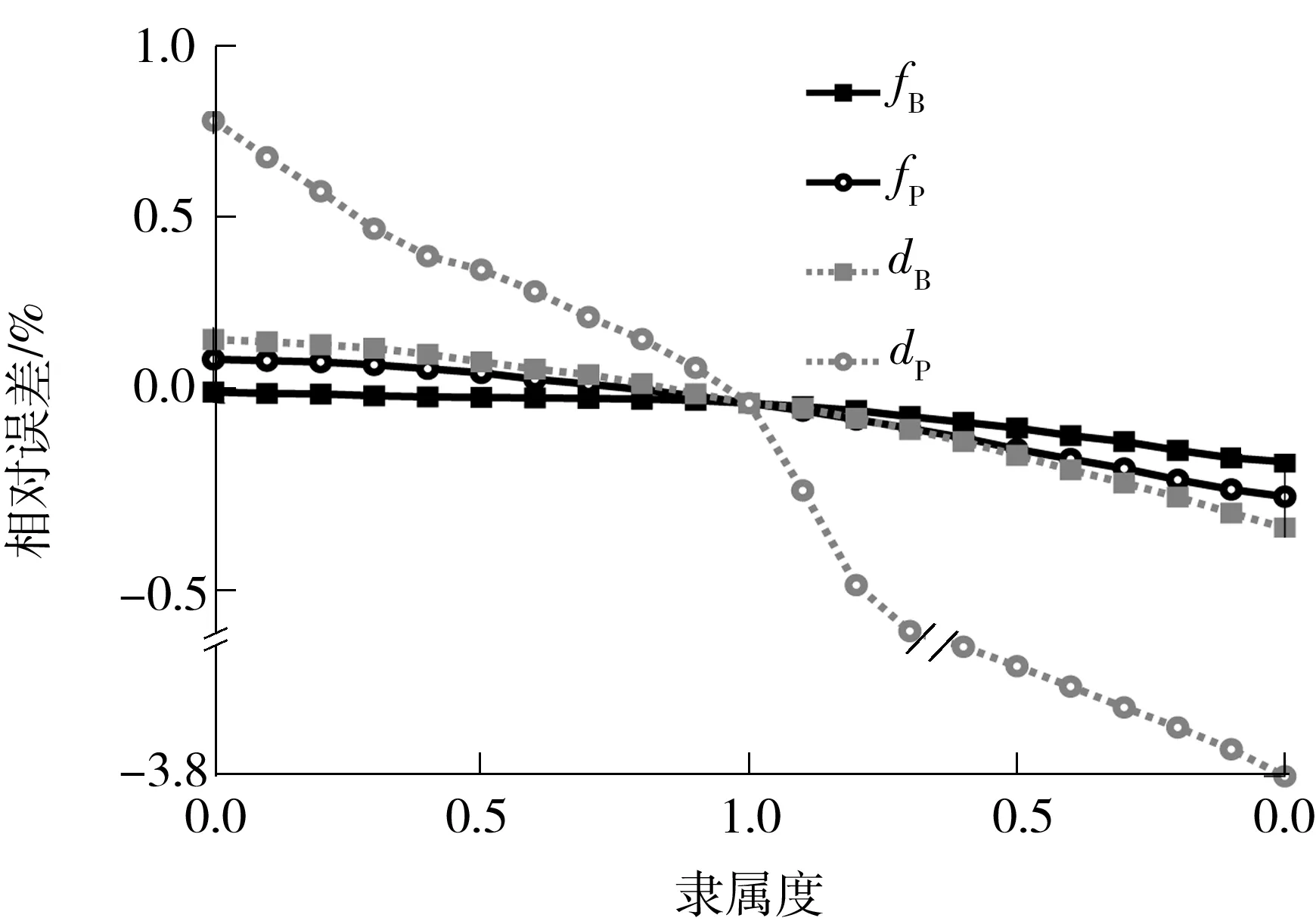
隶属度值“1”左侧表示区间下界对应的隶属度， 隶属度值“1”右侧表示区间上界对应的隶属度

总体而言，无论是固有频率还是解耦率，FPCDM计算结果的相对误差均小于5%，在工程可接受的精度范围内。因此，FMCM和FPCDM的求解结果具有较好的一致性，即FPCDM的计算精度能满足一般工程需求。

此外，在计算效率方面，同一台计算机上求解固有特性响应的离散区间，FMCM用时33 043.4 s，而FPCDM仅用时15.2 s，说明FPCDM具有很高的计算效率。

综上所述，文中提出的FPCDM在求解PMS固有特性的模糊响应时具有良好的计算精度和较高的计算效率，因此可用于后续优化研究。

3.3 PMS模糊可靠性分析与优化

表2 优化前的模糊可靠度Table 2 Fuzzy reliabilities before optimization

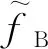
s.t.

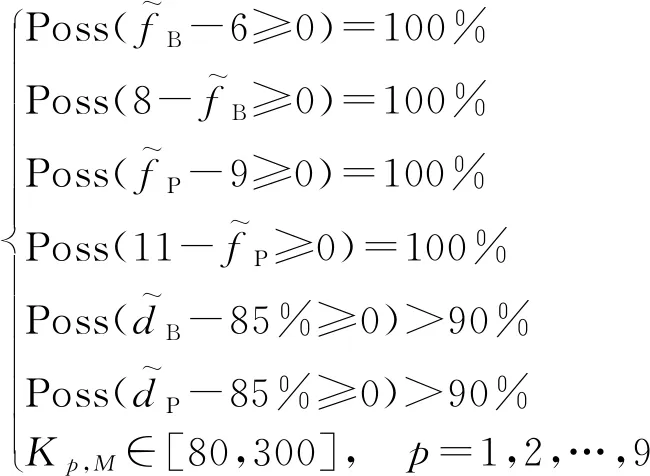
根据图3的优化流程，采用遗传算法对该模型进行可靠性优化。优化后的刚度参数如表3所示，优化后固有特性满足设计要求的模糊可靠度如表4所示。图6给出了优化前后固有特性模糊响应曲线的对比。

表3 优化后的悬置刚度Table 3 Stiffness of mounts after optimization

表4 优化后的模糊可靠度Table 4 Fuzzy reliabilities after optimization

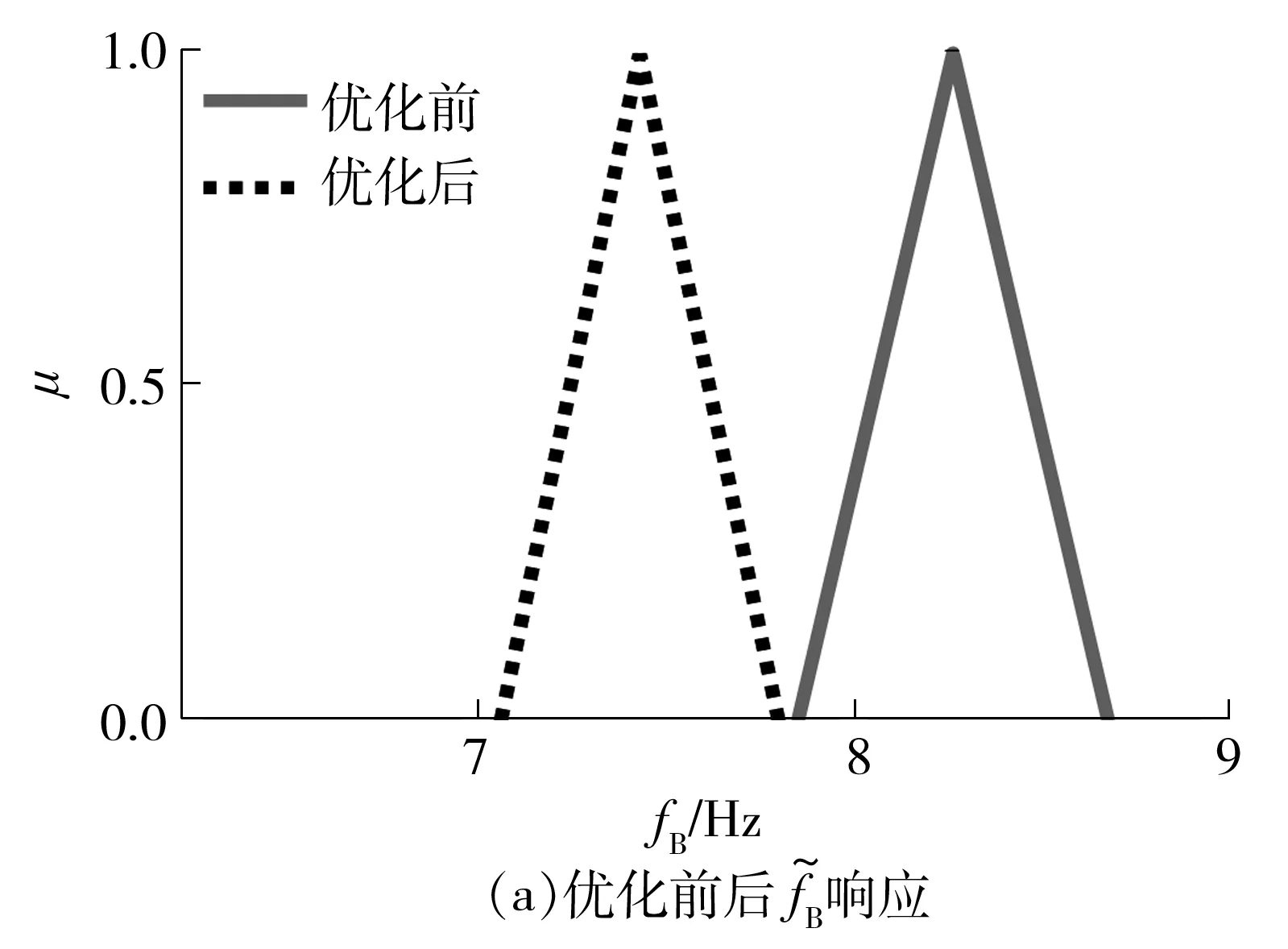
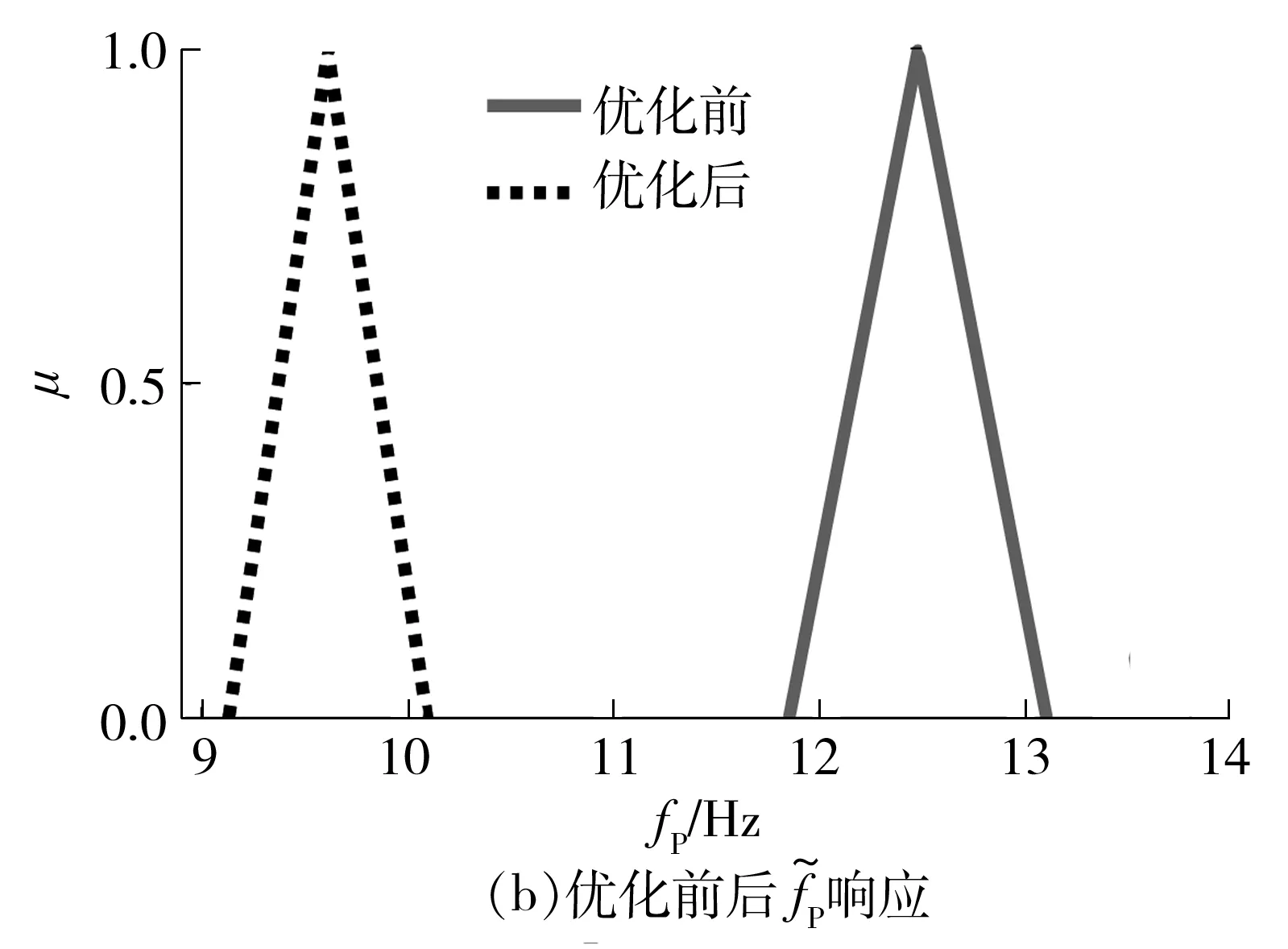
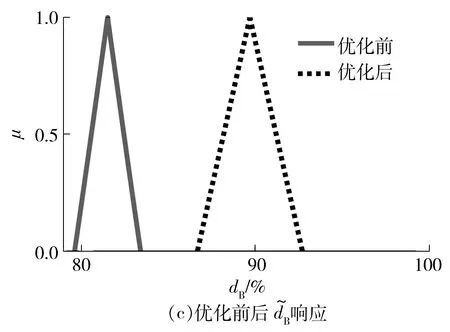
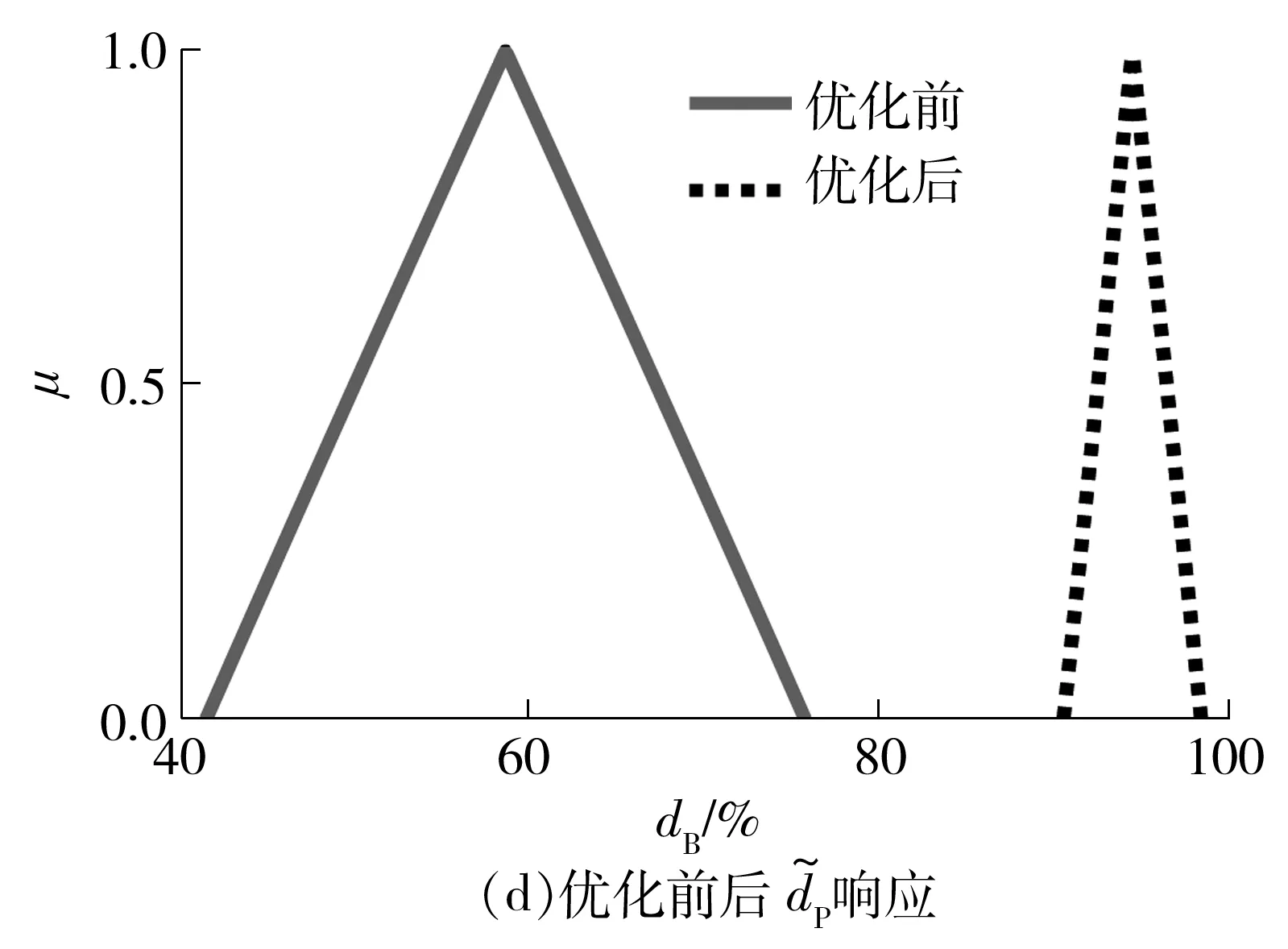
图6 优化前后的响应对比

4 结论

文中针对汽车PMS存在模糊不确定性的情形，推导了求解系统固有特性模糊响应的FMCM和FPCDM方法，并基于FPCDM提出了PMS固有特性的模糊可靠性分析与优化方法。分析结果表明：1)以FMCM为参考，FPCDM能高效地求解PMS固有特性的模糊响应，且具有较高的计算精度，说明FPCDM可有效应用于优化设计研究；2)所提出的可靠性分析与优化方法能有效分析PMS固有特性响应满足设计要求的模糊可靠度，并能可靠地优化PMS的模糊响应。