基于深度学习的办公建筑照明插座能耗多步预测

周璇 雷尚鹏 闫军威

(华南理工大学 机械与汽车工程学院，广东 广州 510640)

建筑能耗约占我国能源消费总量的20%，相比2001年，2016年其涨幅高达144.86%[1]。由于中国公共建筑能耗具有独特的“二元分布结构”特征，大型公共建筑存在着巨大的节能潜力[2]。国家机关办公建筑与大型公共建筑能耗监测平台的建设为基于数据驱动的建筑节能技术研究提供了大量的分类分项运行能耗数据。如何充分利用这些建筑能耗数据进行合理分析与数据挖掘，为建筑用能评价、节能潜力估算、精细化节能管理等提供理论依据，是目前建筑节能领域的关键问题。

照明插座能耗作为建筑电耗分项计量子项之一，占建筑总能耗的27%以上[3]，是建筑节能的重点领域。目前照明插座能耗领域的研究主要集中在能耗预测[4]、用能模式挖掘[5]、变化特性分析[6]、用能评价[7]、预测控制[8]等方面。其中，照明插座能耗的准确预测是能耗异常检测、用能评价等研究的前提。

根据预测步长，时间序列预测方法可分为单步预测和多步预测。单步预测方法仅能预测下一时刻数据，难以用于判断时间序列未来的变化趋势。多步预测方法在判断时间序列变化趋势、提高预测控制效果方面具有明显的优势。现有照明插座能耗预测建模的研究大多集中在单步预测方面，如Mahdavi等[9]分析了办公建筑插座能耗与人行为之间的关联关系，提出了基于随机模型的预测方法，为准确预测插座能耗提供了新思路。Chammas等[10]为提高预测精度，引入温度、湿度等多个环境变量，利用多层感知机方法进行超短期能耗预测，得到的预测效果优于线性回归、支持向量机(Support Vector Machine，SVM)和随机森林算法。Fu等[11]在天气预报信息与建筑能耗监测平台采集的分项能耗数据基础上，利用SVM算法，以两天的历史数据作为输入，对各个能耗分项进行短期能耗预测，预测效果优于自回归差分移动平均模型和C4.5决策树算法。Kim等[12]在预测过程中引入建筑内部人员密度因素，结果表明，在预测过程中采用“kW/人”的指标对能耗数据进行校准，可将预测精度提高7%。

多步预测具有预测未来一段时间内对象变化趋势的功能，可为优化控制与运行决策提供依据，目前已经广泛应用于风速预测、网络流量预测等领域。Ahmed等[13]以美国堪萨斯州逐时风速数据集为基础，比较了基于非线性自回归神经网络的直接多步预测与递归多步预测两种多步预测策略，发现随着预测步长的增加，多步预测策略的预测精度可提高17.07%。田中大等[14]结合混沌理论与回声状态网络，采用多输入-多输出策略对网络流量进行多步预测，预测值与实际值具有较好的拟合效果，为网络拥塞控制问题的解决提供了技术依据。

照明插座能耗受到诸多因素的影响，如室外光照强度、人员行为等，其时间序列具有随机性、不确定性与非线性等特征，常规的多步预测算法难以保证其预测精度。为此，文中拟探索高精度的多步预测方法，为建筑节能与精细化管理提供理论依据。

深度学习是人工智能领域的重大突破，具有良好的泛化能力与学习速度，是一种特殊的人工神经网络算法(Artificial Neural Network，ANN)，其本质是增加了神经网络结构中非线性映射层的数量，对于复杂输入数据，具有优异的特征学习能力[15]。长短期记忆(Long-Short Term Memory，LSTM)模型是深度学习的一种变体模型，具备长期记忆功能，能很好地适用于电力负荷单步预测研究。Zheng等[16]利用LSTM模型，通过房间设备粒度级别的能耗预测，将家庭层级的电力负荷预测精度提高了10%。Kim等[17]将LSTM模型与卷积神经网络结合，对住宅建筑能耗进行预测，结果表明该方法在逐时与逐日预测上分别比线性回归模型的预测精度高39.37%与13.97%。He等[18]在短期电力负荷预测中采用变分模态分解对原始数据进行处理后，利用LSTM模型进行预测，结果证明LSTM模型在短期电力负荷预测中具有较好的适用性。LSTM和多步预测策略的融合，为多步预测过程中复杂特征提取困难的问题提供了相匹配的解决方案。Ghimire等[19]使用卷积神经网络对太阳辐射进行多步预测，为太阳能模拟提供决策支持工具，该深度学习混合预测模型在单日、单周和单月预测中的误差率均小于基准模型。但是，LSTM算法在长时间序列的多步预测方法中的应用目前尚处于探索阶段，存在较多的问题有待进一步探讨，如多步预测策略的选择、LSTM超参数对预测精度的影响等。

文中以建筑照明插座能耗时间序列为研究对象，探讨LSTM对此类带有不确定性的长时间序列的多步预测建模效果，并讨论深度学习建模过程中的超参数选择问题，以期为建筑照明插座能耗异常诊断与用能水平评价提供基准，并为其他不确定性能耗时间序列的预测提供参考。

1 LSTM模型原理

根据单元结构的不同，深度学习技术可以分为如下4类：卷积神经网络(Convolutional Neural Networks，CNN)、受限玻尔兹曼机(Restricted Boltzmann Machine，RBM)、自动编码器(Autoenco-der，AE)、循环神经网络(Recurrent Neural Network，RNN)[20]。其中，CNN常用于图像识别领域，RBM多用于二分类问题，AE主要应用于数据降维处理，RNN特有的反馈传播神经网络结构使其具备信息记忆能力。

由于受建筑中人行为随机性与不确定性的间歇影响(如灯具开关动作、办公设备开关动作等)，以及办公建筑工作时间的周期性影响，建筑照明插座能耗时间序列具有不确定性、随机性、周期性以及关联性。LSTM模型通过设立“门”模块，保留并强化了RNN对于序列信息的长期及短期记忆能力，弥补了其在长序列数据学习训练过程中的梯度消失与梯度爆炸的缺点[21]，对长短时间序列数据具有较好的应用效果。

给定输入训练集为x=(x1,x2,…,xn-1,xn)，用RNN模型对其进行迭代求解，从而得到隐含层序列h=(h1,h2,…,hn-1,hn)和输出层序列y=(y1,y2,…,yn-1,yn)，具体迭代求解过程如下：

ht=fh(Wxhxt+Whhht-1+bh)

(1)

yt=Whyht+by

(2)

式(1)与(2)中：fh为隐含层神经元的激活函数；Wxh为输入层-隐含层网络权重系数，Whh为隐含层内部的网络权重系数，Why为隐含层-输出层的网络权重系数；bh为隐含层偏置项，by为输出层偏置项。

LSTM模型在处理序列型数据问题上具备长期记忆的能力，是由于细胞单元中包含了遗忘门、输入门、输出门以及细胞状态传递链S，其具体结构如图1所示。

图1 LSTM模型的细胞单元结构图Fig.1 Structure of cell unit in LSTM model

LSTM的“门”机制可归纳为如下3个步骤：

步骤1 细胞状态删除。输入xt、ht-1经sigmoid函数处理后，同细胞状态St-1进行合并计算，称为“遗忘门”，具体如下：

ft=σ(Wxfxt+Whfht-1+WcfSt-1+bt)

(3)

S′t-1=ftSt-1

(4)

步骤2 细胞状态保留。输入xt、ht-1分别经sigmoid与tanh函数处理后，同细胞状态S′t-1合并计算决定状态保留量，称为“输入门”，具体如下：

it=σ(Wxixt+Whiht-1+WciSt-1+bi)

(5)

Sct=tanh(Wxcxt+Whcht-1+bc)

(6)

S″t-1=itSct+S′t-1

(7)

步骤3 细胞状态输出。输入xt、ht-1经sigmoid函数处理后,同经tanh函数处理后的细胞状态S‴t-1合并计算决定隐含层序列输出ht，称为“输出门”，具体如下：

S‴t-1=tanh(S″t-1)

(8)

ot=σ(Wxoxt+Whoht-1+WcoSt-1+bo)

(9)

ht=otS‴t-1

(10)

式(3)-(10)中：ft、it、ot分别为遗忘门、输入门、输出门；Wxf、Whf、Wcf分别为“遗忘门”机制中的输入层-隐含层网络权重系数、隐含层内部的网络权重系数、隐含层-输出层网络权重系数，Wxi、Whi、Wci分别为“输入门”机制中的输入层-隐含层网络权重系数、隐含层内部的网络权重系数、隐含层-输出层网络权重系数，Wxc、Whc分别为当前细胞状态传递链中的输入层-隐含层网络权重系数、隐含层-输出层网络权重系数，Wxo、Who、Wco分别为“输出门”机制中的输入层-隐含层网络权重系数、隐含层内部的网络权重系数、隐含层-输出层网络权重系数；bt为“遗忘门”机制中的偏置项，bi为“输入门”机制中的偏置项，bc为当前细胞状态传递链中的偏置项，bo为“输出门”机制中的偏置项；Sct为当前细胞状态，S′t-1、S″t-1、S‴t-1分别为细胞状态在单元内部传递的不同阶段；σ和tanh分别为sigmoid和双曲正切激活函数。

输入训练集x经过网络权重系数矩阵处理后，在输入层与隐含层间进行传播。结合式(1)与(2)可知，随着隐含层数的增加，模型的非线性表达能力增强。但是，由于数据自身特性的不同，模型准确度与隐含层数、隐含层神经元数等超参数的关系并非单一的线性关系，需要进一步探讨其对预测精度的影响。此外，“门机制”是实现模型长短期记忆功能的结构基础，时间步长(Time Steps)为细胞单元状态传递链St所关联的历史状态的步数，其设定值影响LSTM模型的学习能力、训练速度等，需要根据数据时间特性进行合理设置，是待优化的超参数之一。因此，文中拟结合对象的具体特征，对上述LSTM模型超参数的设置与调试过程展开讨论。

2 基于LSTM的照明插座能耗多步预测方法

本节提出的大型办公建筑照明插座能耗多步预测方法包括数据预处理与模型建立两个主要阶段，具体流程如图2所示。

2.1 数据预处理

照明插座能耗时间序列预处理包括数据清洗与数据转化两个主要过程。

2.1.1 数据清洗

建筑能耗监测平台在数据采集、传输、存储等过程中容易受到噪声干扰、通信中断、传感器故障等问题的影响，产生缺失、突变或非正常零值等异常数据。对于突变或非正常零值异常的检测方法，笔者已在文献[22]中详细描述。上述数据异常点删除后，表现为数据的单点缺失或连续缺失异常，文中将其定义为一般缺失。此外，能耗时间序列还存在一种累计突变，即当数据远传通信中断时，电表仍然不断采集，但是未远传给服务器，通信恢复后，远传数据表现为连续缺失后的数据突变，文中将其定义为累积缺失。为提高预测精度，数据预处理过程需要对上述两类缺失进行插补计算，核心思想为采用对应时刻的历史数据平均值按比例进行缺失填补，累积缺失采用前1～5个工作日的同一时刻在连续缺失值的占比乘以累积突变值进行插补。照明插座能耗时间序列定义如下：

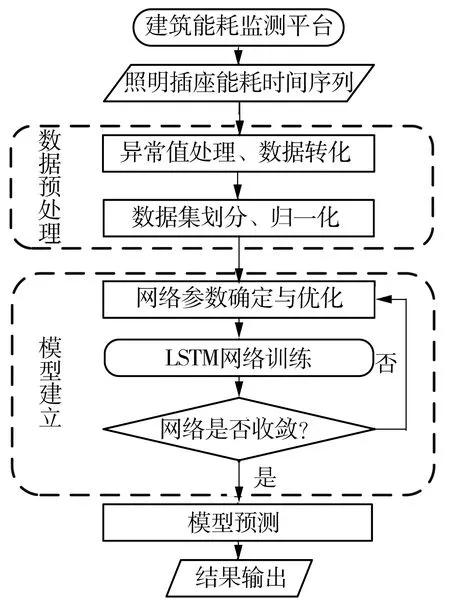
图2 基于LSTM的照明插座能耗预测流程

x=[x1,x2,…,xt1,xt2,…,xtm,xtm+1,…,xN]，

其中N为能耗时间序列总长度，xt1,xt2,…,xtm为缺失数据点，tm-t1+1为缺失数据量。经初步观察发现，能耗时间序列的数据连续缺失数量均未超过24 h，其计算公式如表1所示。

表1 异常数据的离线插补公式Table 1 Formula of offline imputation for abnormal data

表1中：缺失数据x′tj为第j个缺失的插补值，缺失数量共为tm个；xtj-i×24为能耗时间序列前i天相同时刻的历史数据，共取n天，n根据经验设置，默认取5，即当前缺失数据取前5天相同时刻数据的均值。

2.1.2 数据转化

数据转化包括数据归一化和维数转换两部分。

(11)

此外，文中采用的多步预测方法属于多输入-多输出预测方法，模型输入维数与输出维数相同，模型预测输出假设为p维(p取值可以以“日”为单位进行预测，即24的倍数)。因此，数据转化步骤将原始的一维数组转化为p×k阶矩阵。设转化目标维数为m维，k为n除以m的商值向下取整的数值，则有转化过程式(12)：

(12)

2.2 多步预测算法流程

文中提出的多输入-多输出的多步预测算法流程如图3所示。

图3 多步预测算法流程Fig.3 Flow chart of multi-step prediction algorithm

算法的主要步骤说明如下。

(1)LSTM模型的网络超参数初始化

①隐含层数(Layer)：初始值设置为1层，根据数据训练过程在1-3层内进行选择；

②隐含层神经元数(Unit)：结合数据量设定初始值，训练过程中将其逐渐增加，根据训练过程与经验确定；

③迭代次数(Epoch)：所有数据在神经网络中完成1次前向计算与反向传播，结合数据量设定初始值，训练过程逐渐增加，根据数据在训练过程中的表现进行确定；

④批处理量(Batch Size)：获得稳定、精确的梯度下降所设置的单次迭代过程需要的最优样本批量，是深度学习算法中与数据样本数量相关的参数，根据数据量大小进行选择，合理选择单次迭代过程的样本批处理量可以提高模型训练速度与识别精度；

⑤时间步长(Time Steps)：LSTM模型的长期记忆模块中可以利用的时间序列长度，即细胞单元状态传递链St所关联的历史状态的步数，通常根据数据的时间特性进行确定。

(2)模型训练、参数更新

结合超参数调试的结果对模型训练参数进行多次调试、更新，记录模型在训练过程中的损失函数计算结果、训练时间，该算法中损失函数为平均绝对误差(Mean Absolute Error，MAE)，如式(13)所示：

(13)

(3)参数调试

基于数据量大小、数据特性确定超参数合理的取值范围，进而更新不同超参数的组合，为模型训练提供参数取值。

3 算例分析

3.1 数据来源

文中研究对象为夏热冬暖地区某政府机关大型办公建筑，建筑总面积约为10.57万m2，建筑楼层为20层。该建筑于2015年8月建成能耗监测平台，数据采集频率为1 h，能耗时间序列取2017年1月1日至2018年12月31日两年工作日的逐时照明插座分项能耗数据，用于验证LSTM多步预测建模方法的有效性。

3.2 数据预处理

(1)工作日数据提取

建筑照明插座能耗受人的行为影响明显，因此提取工作日能耗进行计算。根据2017—2018年法定节假日与双休日制度，原始数据为两年共730个自然日数据，分离法定节假日共22 d、双休日209 d，最终工作日总数为499 d。

(2)异常数据处理

文中选定数据记录共11 976个，根据2.1节的异常数据处理方法，检测出异常数据为154个，异常率为1.285 9%，如表2所示，然后采用数据插补算法进行异常数据插补。

表2 异常数据检测结果Table 2 Results of ditection for abnormal data

(3)数据转化

照明插座能耗数据需进行归一化处理与维数转化，以提高模型训练过程中的收敛速度，满足输入数据的格式要求。政府办公建筑照明插座能耗时间序列呈现周期性，文中的多步预测时长取单日和单周，即一次性预测24 h和120 h的能耗数据，以验证LSTM模型在照明插座能耗多步预测中的有效性。单日预测条件下，数据格式转化为499×24的矩阵；单周预测条件下，由于数据数量不是120的整数倍，因此舍弃最后96个数据点，将数据格式转化为99×120的矩阵。为了分析单日与单周逐时能耗数据的离散分布情况，绘制箱型图如图4和5所示。

图4 单日逐时能耗分布的箱型图Fig.4 Box plot of hourly energy consumption in weekdays

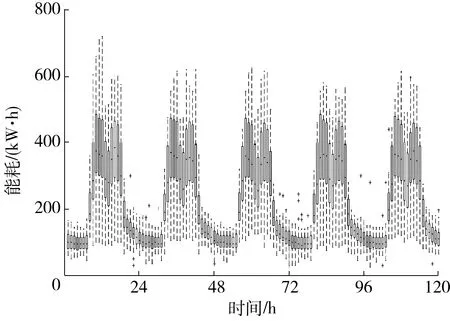
图5 单周逐时能耗分布箱型图Fig.5 Box plot of hourly energy consumption in weeks

如图4所示，该建筑照明插座能耗在午休时段(12:00—14:30)的中位数略微降低，日间工作时段(8:00—18:00)的数据离散度明显高于夜间时段(0:00—8:00和18:00—24:00)，日间能耗最高时段(9:00—10:00)的中位数是夜间最低能耗时段(2:00—3:00)的3.8倍。上述数据的离散分布特征说明建筑照明插座能耗与工作时间具有较强的关联特性，即与人在室内的行为存在较强关联。

如图5所示，该建筑照明插座能耗中位数在工作日内均呈现典型的“M”型分布，每天的用能规律相似，但不同工作日的相同时刻能耗数据的波动范围均不相同，具有随机性与周期性，满足LSTM预测模型对时间序列特征的要求。

将原始数据集按照训练集与测试集为3∶1的比例进行划分。训练集为前75%的数据，测试集为后25%的数据。

3.3 数据建模

文中将提出的LSTM模型预测精度与BP神经网络模型、最小二乘法支持向量机模型进行了比较。三者均运行于Spyder开发环境的Tensorflow框架，LSTM模型使用Keras深度学习库实现，BP神经网络模型、最小二乘法支持向量机模型采用Sklearn库实现。

3.3.1 LSTM模型的超参数寻优

LSTM模型的超参数目前没有普适性的方法进行确定，文中采用试错法进行参数调整。LSTM模型的超参数包括隐含层数、隐含层神经元数、迭代次数与时间步长。

(1)隐含层数

当隐含层数分别为1、2、3时，24 h与120 h多步预测的MAE随迭代次数的变化如图6所示。迭代过程中其他参数设定如下：隐含层神经元数为50,迭代次数为200,批处理量为全批次,时间步长分别为20和4。

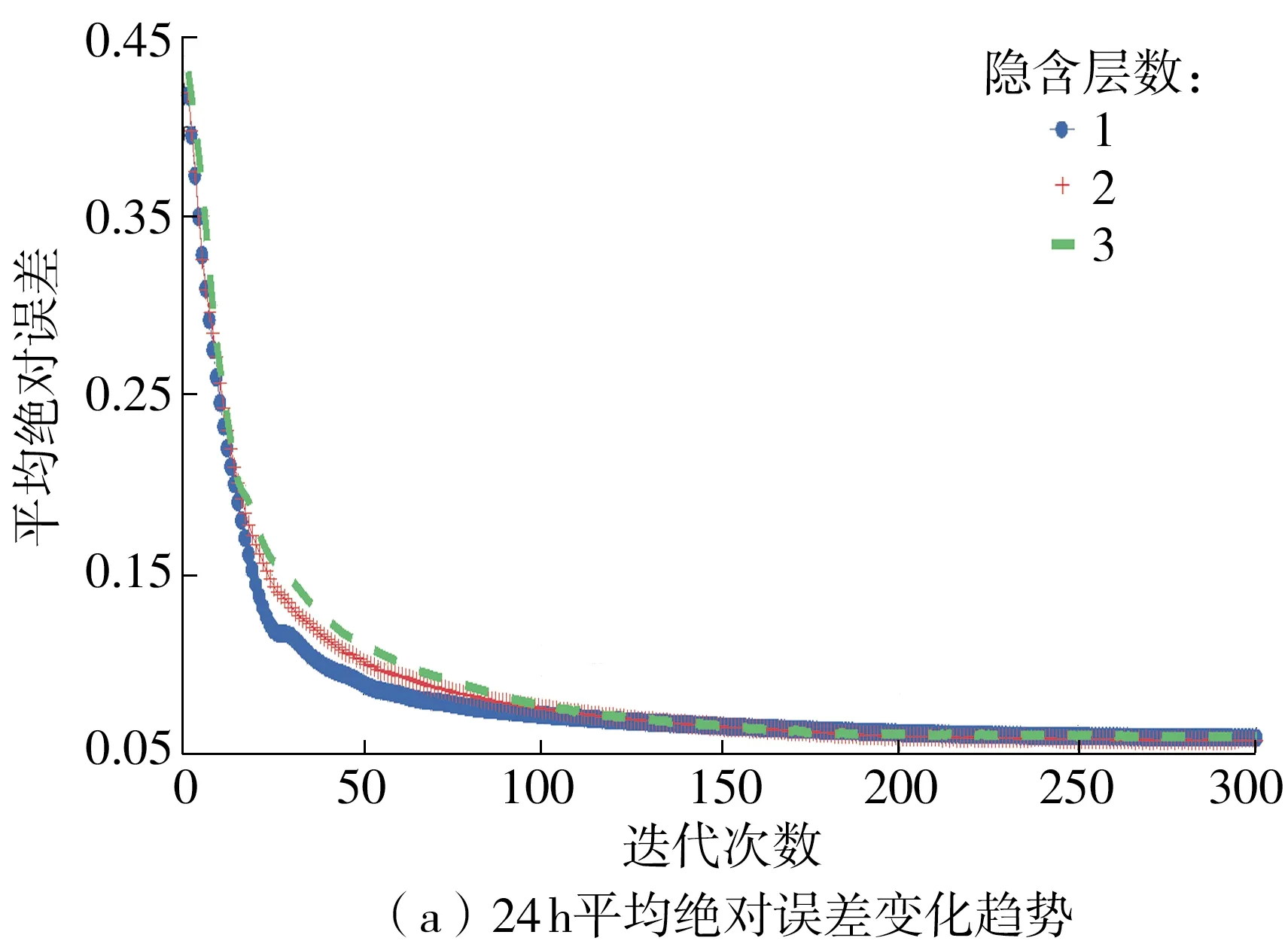
图6 隐含层数对预测精度的影响Fig.6 Effect of hidden layers on prediction accuracy

从图6可以看出，训练初期随着迭代次数的增加，MAE不断降低，预测精度提高，且隐含层数的增加在一定程度上加快了MAE的收敛速度，但影响不明显。24 h与120 h多步预测中，隐含层数对误差影响的变化趋势分别在迭代10与40次后基本重叠，而随着神经网络应用过程中数据量的增加与神经元数等参数的调整，训练迭代次数会逐步增大。由图6可知，隐含层数对模型精度的影响在多次迭代后趋于稳定，因此考虑模型精度，优先选取模型隐含层数为1。为进一步验证此隐含层数，对不同隐含层数下的模型训练时间进行比较，结果见表3，可知隐含层数增加会明显造成训练时间的大幅增加。

表3 不同隐含层数下模型训练时间的比较

综合考虑模型精度与训练时间，文中在24 h与120 h多步预测中将模型隐含层数均选择为1。

(2)隐含层神经元数与迭代次数

分别设置隐含层神经元数为10、50、100与10、50、100、200，讨论隐含层神经元数对预测精度的影响，24 h与120 h的多步预测MAE变化如图7所示。

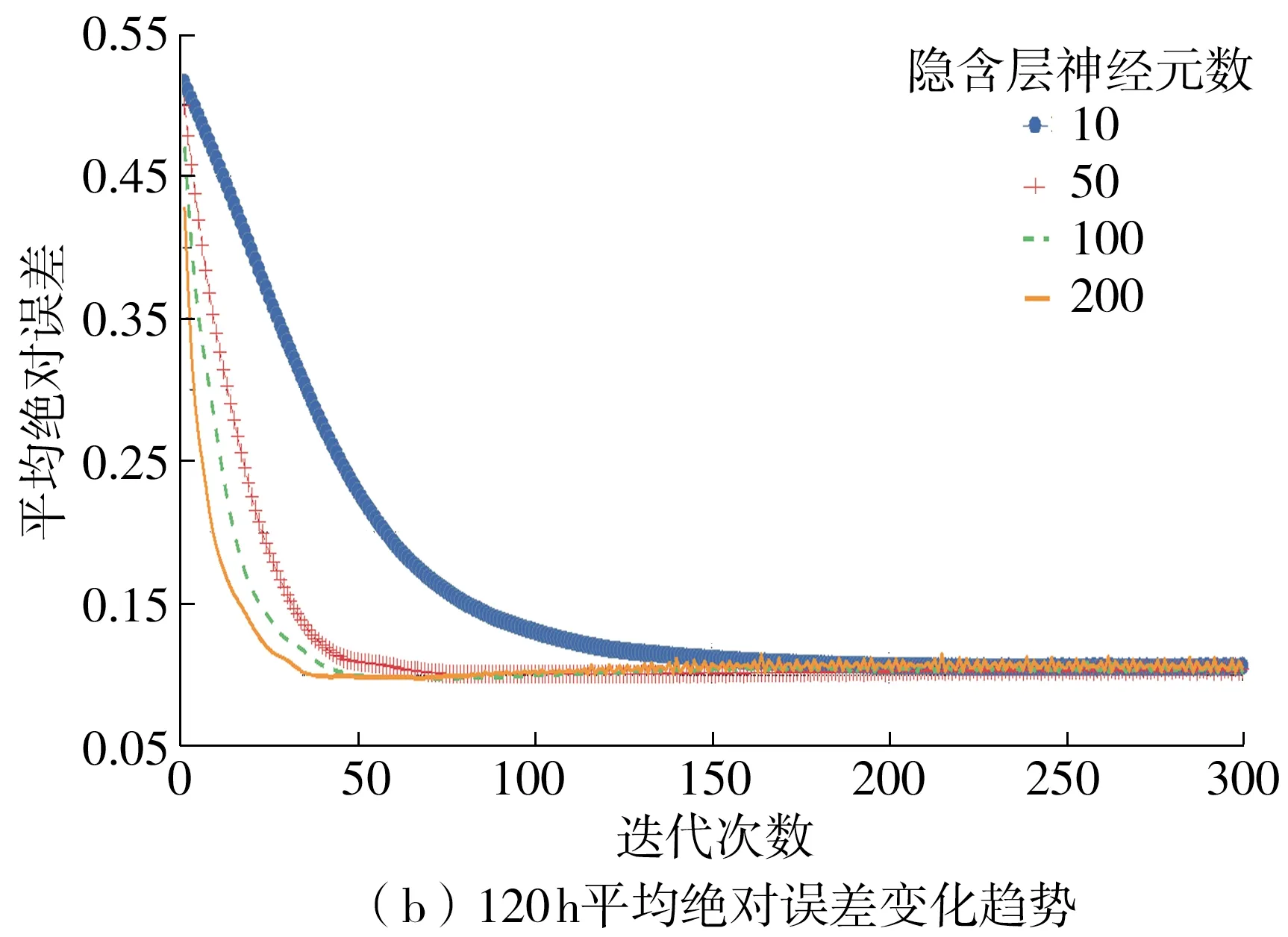
图7 LSTM模型的网络训练过程Fig.7 Training process of LSTM model

从图7中可以看出：随着隐含层神经元数的增加，MAE的收敛速度不同程度地加快。对于24 h多步预测，神经元数为50时的收敛速度远远高于神经元数为10时的速度，神经元数为100时的收敛速度与神经元数为50时的基本一致；对于120 h多步预测，随着神经元数的不断增加，MAE的收敛速度不断提高。

由此可见，不同预测步长下的模型精度均随隐含层神经元数的增加而提高。同时，随着模型训练迭代次数的增加，达到收敛时，不同隐含层神经元数的预测误差基本相同。当隐含层神经元数高于50时，24 h和120 h多步预测在50次迭代后，模型误差下降趋势趋于稳定，因此分别将隐含层神经元数设为50，迭代次数设为50次。

(3)时间步长

时间步长根据照明插座能耗数据的规律特性确定，其能耗受建筑内部人行为的影响较大，而季节变化与人行为强度存在较强的关联性。考虑季节变化规律，对于不同预测步长，文中均以1个自然月为基准，24 h与120 h多步预测分别设置为20和4步。

综上，本算例的LSTM多步预测中，不同预测步长下的超参数调试结果汇总于表4。

表4 LSTM模型的超参数设置Table 4 Hyperparameters setting of LSTM model

3.3.2 其他影响因素分析

能耗监测工作中，综合考虑照明插座能耗分项的相关研究较少，文中对预测过程中的相关算法影响因素进行了分析。

(1)批处理量

批处理量的选择与样本数据量相关，其范围在1至N(样本量)之间。当取值为1时，即每次只训练1个样本；当取值为N时，即为全批次处理。若数据集比较小，当选择较小批处理量时，由于数据噪声的存在，模型梯度下降的方向容易被干扰。因此，在样本数据量较小的情况下，为使梯度下降的方向更为准确地朝向极小值，应优先选用全批次处理。

文中采用多输入-多输出的预测策略，输入与输出维度的增加导致样本数处于全批次处理的可接受范围，因此，本例在不同预测步长中均选择全批次处理方式。

(2)训练样本数据量

训练样本数据量对深度学习模型的预测效果有重要影响。文中分别对24 h与120 h多步预测中训练样本数据量对LSTM多步预测精度的影响展开讨论。为确保开展多步预测所需的样本数据量，24 h与120 h样本初始值分别设定为50与20。对于24 h多步预测，训练集数据量为375个，在50～375的范围内按间距50进行不同训练样本数据量的分析；对于120 h多步预测，训练集数据量为75，在20～75的范围内按间距5进行不同训练样本数据量的分析，结果如图8所示。

图8 LSTM多步预测精度随训练样本数据量的变化

总体看来，针对本算例的研究对象，24 h和120 h的LSTM多步预测误差随样本数据量的增加呈现出明显的逐渐降低的趋势。MAE变化速度总结如下：①24 h预测中，样本数据量达到150后，误差降低趋势渐缓，但MAE仍不断下降；②120 h预测中，在样本数据量达到25后预测误差降低趋势渐缓，但与24 h预测不同的是，其在下降过程中稳定性不足，在样本数据量增加到一定程度后，会呈现较大幅度的误差下降。MAE变化幅度总结如下：①24 h预测的样本数据量从50增加至350(增幅为初始样本数据量的6倍)时，MAE降低24.13%；②120 h预测的样本数据量从20增加至70(增幅为初始样本数据量的2.5倍)时，MAE降低1.3%。

由此可见，样本数据量对深度学习模型预测过程的影响较大，且二者之间并非呈简单的线性关系——初始阶段，预测精度随样本数据量的增加而快速提高，呈正相关；当样本数据量超过某一阈值后，预测精度受样本数据量影响较小。因此，为确保多步预测精度，需要根据研究对象的时间序列特征来确保预测训练集的数据量。

3.4 结果分析

3.4.1 评价指标

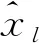
(14)

(15)

(16)

(17)

3.4.2 结果分析

为验证照明插座能耗LSTM多步预测方法的有效性，分别比较LSTM多步预测方法与BP神经网络算法、LSSVM算法的预测精度与训练时间，结果如表5所示。3种方法的运算环境均为i7-6850K处理器、64 GB内存、GTX1080显卡。

表5 不同预测步长下各预测指标的比较

从表5中可以看出，24 h(单个工作日)的LSTM多步预测方法的评价指标与训练时间均优于BP神经网络算法和LSSVM算法。其中MAPE和R2比BP神经网络算法的分别高3.27%、7.57%，EEP与CV(RMSE)高21.07%；与LSSVM算法相比，LSTM同步预测方法的MAPE、R2分别高2.96%、1.49%，EEP与CV(RMSE)高6.23%。

当预测步长增加至120 h(单周工作日)时，3种算法的预测精度均呈现不同程度的下降，以LSTM模型最为明显，LSSVM算法次之，BP神经网络算法的变化最小。横向比较LSTM模型的24 h与120 h多步预测结果，发现后者在样本数据量降低时，训练时间迅速减少，预测精度也随之下降。结合3.3.2节中训练样本数据量对预测精度的影响分析，LSTM模型的预测精度与数据量在初始阶段呈正相关，此后随数据量增加预测精度缓慢提高，120 h预测的数据量偏低，因此随着数据量的累积，预测精度存在一定的上升空间。

在测试集范围内随机抽取两个工作日和两周的预测结果与实际数据进行比较，结果见图9和10。

图9 LSTM模型预测结果的比较(24 h)

图10 LSTM模型预测结果的比较(120 h)

与BP神经网络算法、LSSVM算法相比，24 h预测步长条件下，LSTM多步预测方法在绝大部分峰值点的实际值与预测值的偏差更小，120 h预测步长条件下，LSTM多步预测方法在绝大部分峰值点的实际值与预测值的偏差更大，这与表5中得到的结论相符。比较LSTM模型的预测值与实际值，总结如下：①24 h预测结果与实际数据在下班时段较为符合，但在10:00—11:00以及15:00—16:00期间，由于用能人行为密集发生以及政府部门对外办公时室内人员数量的波动，预测值与实际值出现偏离；②120 h预测结果具有24 h预测用能密集时段波动大的特点，除此之外，预测值与实际值之间的偏差主要出现在峰值点，峰值往往是极大或极小的能耗，受其他因素影响，变化幅度大，规律难以提取，在120 h的较长预测过程中，样本数据量较少，提取的特征不够充分，出现部分峰值点误差较大的现象。

仅从算法角度考虑，LSTM模型的训练时间较短。虽然对于文中研究对象而言，训练时间的长短可以忽略不计，但是对于其他应用，如电力负荷预测、优化控制等，仍需考虑训练时间的影响。

不论是24 h单个工作日预测还是120 h单周工作日预测，LSTM模型均表现出较好的鲁棒性；BP神经网络算法的稳定性相对较差，存在明显的预测偏离点；LSSVM算法在单周工作日预测中表现出对小样本问题的较好适应性，但在单个工作日预测时稳定性降低。

4 结语

随着建筑用能水平评价、能耗异常诊断以及建筑节能等工作的深入开展，不确定性长时间序列的多步能耗预测成为了上述工作的研究基础。文中结合LSTM模型的信息记忆功能，提出了基于LSTM深度学习的多步预测方法，以办公建筑照明插座分项能耗长时间序列为研究对象，结合能耗数据离散分布特征，分析了LSTM模型超参数以及样本数据对模型多步预测精度的影响，得到以下结论：

(1)采用多输入-多输出的多步预测策略，可充分发挥LSTM模型对潜在时序特征的提取优势，与BP神经网络、最小二乘法支持向量机相比，当预测步长为24 h时，其预测平均精度分别提高了13.25%与4.23%，有效提升了照明插座能耗预测的准确性;

(2)结合LSTM模型的超参数调试过程，网络隐含层数对预测精度影响较小，但神经元数需要优化选取，并且模型精度达到稳定所需的迭代次数与训练样本数据量紧密相关;

(3)LSTM模型多步预测过程中，训练样本数据量的增加会明显降低预测误差，并且在相同预测条件下，LSTM模型训练所需时间更短，效果更佳。

文中对算法应用过程中的参数及影响因素进行了分析，所提出的LSTM多步预测建模方法是深度学习技术在照明插座能耗领域应用的初步尝试。后续工作中将在深度学习算法的初步应用基础上，采用更先进的深度学习方法开展研究，尝试提高大数据背景下的照明插座能耗预测效果。