引入参数更要用活参数

范金泉 (江苏省宿迁市马陵中学 223800)

在代数的解题过程中引入参数帮助解题，就犹如几何证明过程中在图形上添加辅助线一样，是一个极为常见的数学方法．当从条件到结论之间的过程不明朗或思路受阻的时候，常常通过一个“无中生有”的创造性过程，引入参数或添加辅助线，使条件到结论之间的关系清晰、过程明朗，从而完成问题的求解．

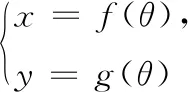
1 一字之差，由易变难

例已知实数x,y满足2x2+y2=1，求x2+2xy的最大值．

分析 本题属于容易题，直接使用不等式2xy≤x2+y2，即可求解．

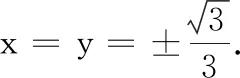
变题1已知实数x,y满足2x2+y2=1，求x2+2xy的最小值．

从例题到变题仅一字之差，即由“最大值”变为“最小值”，而题目的难度却发生了很大的变化，由一道相当容易的习题变成了一道颇难的习题，主要是因为如果再试图直接使用不等式2xy≤x2+y2求解(比如下列两个过程)就会遇到障碍，使得问题无法求解．

探究1因为∀x∈R，x2≥0，所以应当在2xy<0即在x与y异号的条件下，x2+2xy才有可能取得最小值．

而当x与y异号时，显然有-2xy≤x2+y2，即x2+y2≥-2xy，所以x2+2xy≥-y2．又因为2x2+y2=1，所以y2≤1，所以-y2≥-1．能否说x2+2xy的最小值就是-1呢？显然不能．因为当y2=1时x=0，此时x2+2xy=0，故无法取得最小值-1．

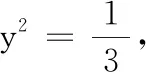
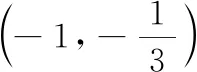
之前的两种方法，就是因为没有找到使得x2+2xy取到最小值时实数x,y之间的关系，从而使得问题求解无法继续下去．为此，想到引入参数k帮助问题的求解．

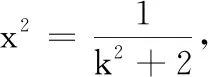
反思1由方程2x2+y2=1确定的是一条封闭的曲线，故代数式x2+2xy不仅有最大值，也有最小值．但由“最大值”变“最小值”，仅一字之差，为什么求解的方法大相径庭？有没有相同或相似的方法，既能求出最大值又可以求出最小值呢？

答案显然是肯定的！在上述的解题过程中，当1+2k>0时，即可求得x2+2xy的最大值，但和直接使用基本不等式相比显然太烦琐，不宜提倡．解决问题的重点是能否像直接使用基本不等式求最大值那样，比较直接地求出最小值.答案还藏在不等式2xy≤x2+y2里．

2 用活参数，化繁为简

2.1 打破刚性约束，拓展思维空间

当我们看到式子2xy时，会不由自主地想到不等式2xy≤x2+y2．而该不等式中的等号当且仅当x=y时成立，限制条件过于刚性，不能适用于在y=kx条件下不等式的应用．

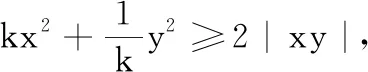
上述解题过程旨在保持条件2x2+y2=1完整的前提下，将2xy用只含有x2与y2的式子来表示，通过参数k予以调整、凑配，思路明晰，方法统一，既求得最大值也求得了最小值，一举两得．

2.2 逆向思维，丰富路径

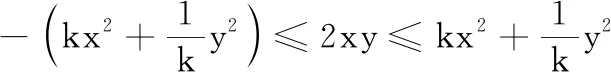
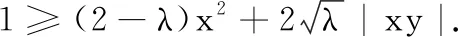
2.3 从孤立到整体，方法更一般

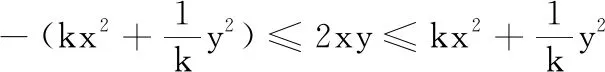
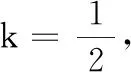
3 举一反三，触类旁通

3.1 改变符号，挖掘结论的对称性

变题2已知实数x,y满足2x2+y2=1，求x2-2xy的取值范围．

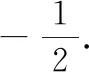
3.2 由点到面，挖掘结论的一般性

变题3已知实数x,y满足2x2+y2=1，对任意的实数λ，求x2+2λxy的取值范围．

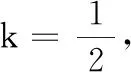
3.3 加强变式练习，挖掘结论的灵动性

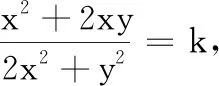
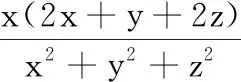
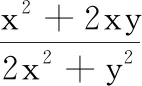
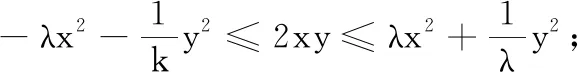
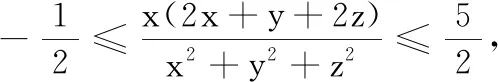
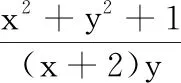
分析 变题5是将变题4中的z变成了具体的数字1，本质没变，故方法依旧．又由于将任意实数变为了正实数，只需要讨论一个方向．

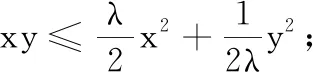
4 深度反思，山水依旧

宋代禅宗大师青原行思提出参禅的三重境界：参禅之初，看山是山，看水是水；禅有悟时，看山不是山，看水不是水；禅中彻悟，看山仍然山，看水仍然是水．参禅的三重境界何尝不是学习的三重境界呢？看山是山：在学习的基础上通过归纳推理形成感性认识，初步认识事物的表象．看山不是山：在感性认知的基础上，通过思维训练、大脑加工、逻辑理解上升到理性认识，把握事物本质和规律．看山还是山：将理性认识运用到实践中去，指导行动，达到知行合一．

上述过程中，看到2xy，不由自主地想到不等式2xy≤x2+y2，这只能说是达到了第一境界，即“看山是山”．为了打破“x=y”的刚性要求而引入正实数k，使不等式2xy≤x2+y2变为2xy≤kx2+y2，应该算是进入了第二境界，即“看山不是山”，而是“横看成岭侧成峰”了，运用裕如，游刃有余．如何才能进入第三境界，达到返璞归真，回归“看山还是山”呢？要完成这一步，重在反思领悟！

为了解答这个问题，我们不妨将x2+2xy分解为x(x+2y).显然，原问题可以看作是研究与揭示x与x+2y之间的和与积的不等式关系！

设x2+2xy=k，即x(x+2y)=k，所以λx(x+2y)=λk，其中λ>0．又(λx)2+(x+2y)2=(λ2+1)x2+4xy+4y2=[(λ2-1)x2+4y2]+2(x2+2xy)．令(λ2-1)∶4=2∶1，解得λ=3．即(3x)2+(x+2y)2=4(2x2+y2)+2(x2+2xy)=4+2k．

若x与x+2y同号，(3x)2+(x+2y)2≥6x(x+2y)，即4+2k≥6k．所以k≤1．等号成立的条件是3x=x+2y，即x=y．即x2+2xy的最大值为1，当且仅当x=y时取得．

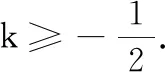
数学之美，在于对真理的不懈追求.透过一道极其简单的数学问题探寻其中的数学内涵，由简到繁，再由繁到简，不仅做到由感性认知上升到理性认知，而且达到知行合一的境界.这才是有美、有味、有蕴的数学！