深挖练习价值，让解决问题有据可依
——以人教版教材五上中的一道习题为例

2020-11-30 12:10赵银微

教学月刊(小学版) 2020年32期

□赵银微

人教版教材五年级上册第43页练习十第4题，学生的错误率很高。该题涉及的信息很多，比如除法算式的意义、“每份数”概念的理解以及常见的数量关系等。一部分对这些数学信息（或者部分信息）掌握不扎实或不准确的学生，在面对多种数学信息的交汇时无所适从，导致解题错误。笔者就学生的错误情况进行了分析，认为主要原因是学生对核心概念理解不清晰、信息整理浮于表面、数量关系不清等。

笔者认为，会分析数量关系是正确解决问题的关键。如何让学生从具体情境中抽象出数量关系式，再应用到具体情境中去？如何由一题想到一类问题的解决，拓展学生的思维，进行有效教学呢？

【策略思考】

（一）引导加深对概念意义的理解

分析数量关系的前提是让学生明晰数量关系的各部分名称，也就是弄明白“每份数”（单价、速度、工作效率）的概念。这就要求教师在教学四年级上册“速度、时间和路程”这一内容时，要让学生对速度的概念领会透彻。笔者是这样开展教学的。

为了让学生更好地理解速度的意义，教师把教材情境图中的内容改成“动物跑步比赛，兔子小姐4分钟跑了280米，狐狸小姐花了3分钟跑了240米，谁跑得快？”

1.比一比

独立思考：什么是相同的？比什么？你是怎么样让它们一样的？

生：我先求出兔子小姐和狐狸小姐1分钟跑的路程。280÷4=70（米），240÷3=80（米），70＜80，所以狐狸小姐跑得快。

生：我是通过画图来帮助理解的。把280米平均分成4份，狐狸1分钟跑的路程就是1份。比较1份就可以了。

2.速度意义的理解

师：那70表示什么？生：应该是路程。生：完整地说是兔子1分钟跑的路程。

师：看来70米不仅表示的是路程，这中间还隐藏着1分钟。80呢？

图1

3.认识速度

师：这样每分、每秒、每时，单位时间行的路程就叫速度。所以，这里的70就是速度。（板书：70米）

生：我们怎么知道这是表示速度？

生：可以写成70米/分，就表示每分钟跑了70米。

4.借助图形得出数量关系式

师：刚才我们认识了速度，现在你觉得速度怎么求？能不能结合同学画的图说一说？

生：路程÷时间＝速度。

生：路程就是总的长度，时间就是有几份，速度就相当于每1份是多少。我们知道每份数等于总数除以份数，所以速度就等于路程除以时间。

在此环节中，教师始终围绕理解速度的意义展开教学，让学生思考：路程、时间都不相同，如何比较快慢？学生的想法精彩纷呈：第一种想法是将时间变得一样，比较路程；第二种想法是将路程变得一样，比较时间。学生通过画图法将抽象的速度具体形象化，也进一步理解数量关系式的意义：路程相当于总数、时间相当于份数、速度相当于每份数。学生透过抽象的数，看到了速度的本质，对速度的理解就自然深刻了。

（二）注重“问题表征”方法策略指导

教材中的“解决问题”多注重以情境图、数据表、对话、文字等形式提供信息、呈现问题。有些信息是隐藏其中的，这就要求学生具有收集信息和识别有用信息的能力。教师就要注重对学生“问题表征”方法与策略的指导，以此来提高学生解决问题的能力。

1.“圈”——明题意

初读题目后，要求学生明确问题的情境是什么，通过“圈”的方式，留下阅读后的痕迹，即关于跑1千米所需时间的问题。

图2

2.“找”——题意易错点

寻找情境中容易错的地方，本题有两个，分别是李大伯只比刘大伯多2分钟，李大伯跑1千米平均所用的时间。

3.“磨”——题意直观化

学生“圈”问题后，再通过“磨”，即初步理解，将信息整理完整，并适当分析信息间的关系。

出示学生作品如下图：

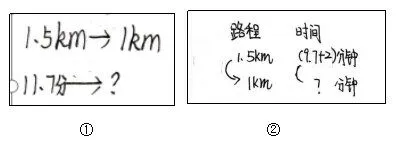
图3

（三）借助几何画图理解数量关系

《义务教育数学课程标准（2011年版）》指出：“几何直观可以把复杂的数学问题变得简明、形象，帮助学生直观地理解数学。”学生借助画图搭建起形象思维和抽象思维的桥梁，在学习理解数学过程中培养和发展几何直观能力，感悟初步的数形结合思想，从而促进数学能力的发展。

【课堂回眸】

师：如果要把这样的关系更形象地表示出来，怎么办？

生：画线段图。

学生反馈：

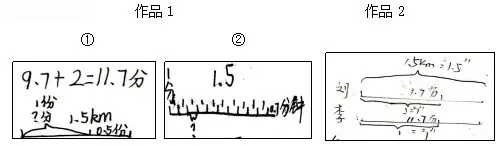
图4

生：第①幅图把1千米看作1份需要多长时间，第②幅图表示每分钟跑多少千米？

生：刘大伯用9.7分钟除以1.5千米，我是把9.7分钟平均分成1.5份，每份是指每千米需要几分钟。

生：所以李大伯是（9.7+2）分钟跑了1.5千米，就是把总时间除以千米数即可。

画图“简缩”了题目中的次要成分，把主要成分直观地展示出来。同时，画图采用数与形相结合的形式，将事物间的数量关系一目了然地呈现出来，学生借助“图”的表征，把数量关系“总时间÷千米数＝每千米所用的时间”十分清晰地表示出来。

（四）巧用递进练习发展学生思维

对于总数、份数、每份数之间的关系，学生的辨识度到底有多高？教学时，教师需要引导学生透过现象看本质，寻找生活中此类关系的应用范例，让学生学以致用。

1.简单应用会辨析

师：先判断下面的2题跟例题一样吗？和同桌一起讨论分析。

图5

例题（9.7+2）÷1.5=7.8（分钟）

师：请仔细观察这两个除法算式，都用了11.7分钟和1.5千米这两个信息，每个算式的意义该怎么理解？

生：看除数，除以11.7就是算每分钟跑几千米；除以1.5千米就是算跑每千米需要几分钟。

生：将11.7分钟平均分成1.5份，每份就是跑每千米需要几分钟；将1.5千米平均分成11.7份，每份就是每分钟跑的路程。

这两个问题，学生很容易混淆，弄不清楚到底谁除以谁，尤其是刚学习了小数除法，部分学生的思维还停留在用“路程÷时间=速度”的数量关系去解决，没有很好地理解“跑每千米需要多少时间”这个问题。所以，教师设计简单易混淆练习，组织学生在交流、比较中，及时将原来零碎的思维提炼为有意识的完整的思维，逐渐将学生对解题的感性认识提升为理性认识，真正掌握解题的方法。

2.提升练习会联想

数学的学科特征决定了数学的典型和基本问题是具有类型和结构特征的，学习者常可将新问题转化为经验系统中所熟悉的问题作为解题思路。因此，教师可以设计一些份总关系在不同生活情境中的小练习，使学生对这类数学问题的基本结构和关系模型有较好的领悟与积累，促进学生进行知识间的联想。如：

①已知3.5米铁丝重1.4千克，平均每米铁丝重多少千克？

②王师傅4.25小时做17个零件，每个零件需要多少时间？

③刘老师用8.9元买了7千克梨子，每千克梨子多少元？用1元钱可以买多少千克梨子？（除不尽保留两位小数）

通过对以上问题的解决，学生发现并领悟了一些共性：（1）这些问题虽然情境不同、数据不同，但问题的数学特征和结构关系是类似的：从数量关系上讲，只是涉及的份总关系在不同情境中的具体化，简单讲就是每份数、份数和总数之间的关系；（2）这些问题都是根据除法的意义来解决的，基本模型都是“总时间（千克数）÷个数（钱数）＝每个所用时间（每元买的物品数）。小部分学生会形成思维定式，为了打破这种状态，教师在第③题的基础上又设计了2个问题。如果学生会联想，对这些问题的特征、结构关系等有较好的理解和识别能力，那么他们在解决以下问题时便有了很好的经验基础与数量关系储备，问题解决就很简单了。

④一种越野车在沙漠中行驶100km消耗汽油16升。它要穿越总路程130km的沙漠无人区，至少要准备多少升汽油？

⑤8吨黄豆能榨油3.2吨，榨16吨油需要多少黄豆？

3.解法多样促理解

鼓励解决问题策略多样化，是促进每一个学生充分发展的有效途径。课堂上，教师引导学生从不同的角度去认识问题，采用不同的方式表达自己的解题思路，鼓励学生用不同的方法解决问题。

如解决上面第⑤小题时，教师鼓励学生采用不同的方法，学生用了多种方法解决此题。

出示学生作品：

图6

学生通过自身的独立思考不仅列出了算式，而且对每道算式都说明了理由。这种呈现多样的解决问题方法的设计，促进了学生对问题的多方面理解。对于多数学生来说，这样的经验将促使他们从多个角度思考问题，形成多样化的问题解决意识。

4.拓展练习促生长

数学知识之间是有机联系的，这也是学习知识点和知识点存在的原因所在。教师要从小学数学教材的编写意图着手，从学科教学发展谋局，将拓展练习练在知识延伸线上，让学生感觉到知识的生长和发展方向，有利于孕育后继学习的知识基础和情感需求。

如可以设计这样一道题：

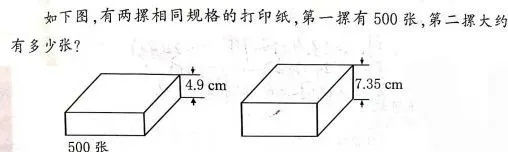
图7

学生作品反馈交流：

图8

这为以后学习几何图形，如求大平面图形可以裁成几个小图形，大立体图形里最多能摆放几个小立体图形的学习奠定了基础，从而形成一定的知识生长点。

如五上题①：有一块长7米，宽1.2米的长方形丝绸，用来做底是0.5米，高是0.4米的直角三角形小旗，可以做多少面？

又如五下题②：茶厂工人要将长、宽各为20cm，高为10cm的长方体茶盒装入棱长为30cm的正方体纸箱里，最多能装几盒？怎样才能装下？

如果从行程问题数量关系的教学考虑，不仅可以让学生理解关系的意义，利用数量关系解答相关题目，还为以后学习正反比例等知识，起到一个渗透的作用。

图9