基于深度学习的对抗样本生成技术研究综述

王晓萌, 陈鸿龙*, 张安庆, 李隽健, 石乐义

(中国石油大学(华东) a 控制科学与工程学院, b 计算机科学与技术学院, 山东 青岛 266580)

人工智能技术自1956年提出以来，其发展经历了复杂而又漫长的过程.目前人工智能在不同应用领域都取得了极大的成就，被视作推动发展的新技术.深度学习作为人工智能的核心技术之一，由于当前大型及代表性数据集的可用性，已经被广泛用于各个领域，如计算机视觉[1-2]、医学图像分析[3-4]、自然语言处理[5-6]以及其他相关应用[7-8]等.深度学习给人们带来巨大便利的同时，其安全问题也开始引起人们的重视.例如，系统模型会对添加扰动的输入样本产生误判，即以高置信度来预测出一个错误结果.这些被添加扰动的样本称为对抗样本，近年来成为研究者关注的热点.

对抗样本(Adversarial Examples)，即视为攻击者精心设计的特殊样本，可以导致模型的错误预测.这一概念由Szegedy等[9]首次提出，他们证明在输入图像上添加轻微的扰动，能使得深度学习网络产生错误预测结果，网络中过多的非线性特征和无适当的正则化是对抗样本的存在原因.而Goodfellow等[10]却有着相反的观点，他们认为深度网络的高维线性才是对抗样本存在的原因，继而提出一个快速生成对抗样本的方法——快速梯度符号法(fast gradient sign method, FGSM).自此，生成对抗样本的优化算法不断涌现.尽管对抗样本存在的原因至今没有达成统一的观点，但毋庸置疑，对抗样本的存在必然带来很大的安全隐患，更深入地研究对抗样本的攻防策略是很有必要的.

本文将对抗样本生成的相关研究工作进行汇总，着重选取具有代表性的方法进行原理介绍和分析.本文的基本框架如下：第1章主要介绍对抗样本的起源和基本原理；第2章分类讨论对抗样本生成方法；第3章介绍部分对抗样本生成方法的实验结果；第4章总结了对抗样本在不同领域的应用；第5章指出对抗样本面临的挑战和前景预测.

1 对抗样本的起源和基本原理

对抗样本被定义为在原样本上添加难以察觉的扰动所形成的样本，它可以“欺骗”模型使其产生错误的预测结果，从而大大降低模型的整体精度.

1.1 对抗样本的起源

对抗样本由Szegedy等[9]首次提出，研究表明在神经网络高层中，包含语义信息的是空间而不是单个神经元，同时发现深度神经网络学习的输入输出映射是不连续的，为了干扰网络对图像的预测，增大网络的输出误差来得到难以察觉的扰动，并提出解决以下优化问题，以计算一个能使得图像略微扭曲且能“欺骗”网络的扰动δ：

(1)

式中，t表示特定的目标类别，f表示神经网络分类器.最小化δ取值不唯一且计算困难，因此，使用称为L-BFGS的近似求解方法.通过搜索c的最小值，优化式(2)来得到最小值δ，同时满足条件f(X+δ)=t：

(2)

式中，J表示损失函数.通过求解式(2)中的优化问题，计算能“欺骗”神经网络且满足L2距离最小的对抗样本.这类对抗样本的生成方法，可以推广到不同的模型和训练集中.

1.2 对抗样本的基本原理

深度神经网络是由神经元层组成的大型神经网络.一个神经网络可以简单表示为：fθ:X→Y，其中X表示输入，Y表示输出，θ表示模型训练学习的参数.对于监督式学习任务，模型学习的目的是找到最优参数，使得网络模型预测fθ(X)和真实标记Y的差异最小化，通常这个差异用损失函数J(fθ(X),Y)来衡量.

对抗样本是在测试阶段利用数据扰动使得神经网络做出错误预测，从而降低模型的整体精度.例如，图像中添加的扰动难以被肉眼识别，却能使模型产生错误的分类结果.对抗样本可被归结为下式：

Xadv=X+δs.t.D(Xadv,X)<ε

(3)

式中，δ表示添加的扰动，D(X,Xadv)表示原始图像与对抗样本的差距，显然这个差距要尽可能小.对于无特定目标攻击来说，对抗样本的目的是使f(Xadv)≠f(X)；而对于特定目标攻击，其目的是使f(Xadv)=t，t为某一目标标记类别.

对于上述描述，可以总结为优化问题.对于无特定目标攻击，攻击者感兴趣的是与正确输出不同的任意输出，即最大化损失函数使得预测朝着错误的方向：

maxJ(f(Xadv),y) s.t.D(Xadv,X)<ε

(4)

依照上式优化对抗样本，使得模型输出偏离原始预测结果.

对于特定目标攻击，给定一个目标输出t，则优化问题为

minJ(f(Xadv),t) s.t.D(X,Xadv)<ε

(5)

在给定目标输出的情况下，最小化损失函数使模型得到目标输出，即使得深度神经网络对抗样本的预测为指定标记类别.

2 对抗样本的生成方法

对抗样本的生成方法可以从以下几个角度进行划分：期望输出、攻击方式和攻击策略[11].

对于模型的期望输出，对抗样本的生成方法可以分为无特定目标攻击(Non-targeted Attack)和特定目标攻击(Targeted Attack).无特定目标攻击又被称为非目标针对性攻击，其对抗性输出不指定类别，只产生尽可能多的错误分类.特定目标攻击又被称为目标针对性攻击，其对抗性输出为特定的类别，基本上独立于添加了扰动的输入点.

对于添加的扰动范围，又可以分为特定、语境和通用范围.特定范围的攻击是针对一个特定的输入图像而设计的扰动，相同的扰动不一定会使模型中的其他数据点预测错误.语境范围的攻击是创建一种固定的图像不可知的扰动，该扰动会导致针对一种或多种特定上下文情况的标签更改.例如，扰动适用于下雪或下雨天的交通情况，能够在大多数的角度、距离和光照下“欺骗”模型.通用范围的攻击是创建一个固定的图像不可知的扰动，该扰动会导致真实数据分布的重要部分的标签更改，而没有明确的上下文相关性.

对于攻击方式，生成方法可分为白盒攻击和黑盒攻击，其中黑盒攻击包括输出透明、标签透明、查询限制和完整的黑盒攻击.白盒攻击的攻击者充分了解模型的内部知识，包括具体的体系结构、所有参数和权重配置以及可能的训练策略.在输出透明的黑盒攻击中，对手无法检索模型参数，但可以观察模型输出的全部或部分分类概率；标签透明的黑盒攻击既不能访问相关的模型参数，也不能访问类别概率或对数，但可以观察系统最终分类决策的全部或部分内容，即只能访问推断的标签；对于查询限制的黑盒攻击，对手无法访问相关的模型参数，但可以在有限数量的输入或有限频率下观察模块输出的全部或部分内容；而在完整的黑盒攻击中，对手既不能检索相关模型参数，也不能直接观察模型的输出.

对于攻击策略中的优化方法，可以分为一阶方法、二阶方法和进化与随机抽样等三种.在一阶方法优化方式中，试图利用精确或近似梯度给出的扰动方向进行优化；二阶方法优化的扰动搜索基于Hessian矩阵的计算或Hessian矩阵的近似值；基于进化与随机抽样优化的方法是通过对分布进行抽样并组合有潜力的数据来产生可能的扰动.

2.1 特定目标攻击

2.1.1 白盒攻击

(1)快速梯度符号法(FGSM)

Goodfellow等[10]通过调整输入图像的每个像素来创建扰动图像，从而使预测结果变差，算法如式(6)所示：

Xadv=X+ε·sign(xJ(X,θ,ytrue))

(6)

式中，X为原始图像，通常为3D张量(宽度×高度×深度)，像素的值是[0，255，255]范围内的整数，ytrue是原始图像X的真实标签，ε是扰动强度，xJ(X,θ,ytrue)为分类模型的交叉熵值.

(2)ILCM法[12]

为了能应用于类别数量大、类别之间差异程度大的数据集，实现无特定目标攻击到特定目标攻击的转换，在I-FGSM的基础上根据原始图像X上训练网络的预测，选择了可能性最小的类别作为模型指定的错误类YLL：

(7)

(8)

随后Madry等[13]发现在105个随机起点处发现的交叉熵损失的局部最大值是不同的，但对于正常训练和对抗训练的网络，它们都有相似的损失值，据此提出了攻击仅依赖于一阶信息的观点.

(3)雅克比映射攻击(JSMA)

Papernot等[14]提出利用前向导数来生成对抗样本，利用Jacobian 矩阵来生成前向导数，如式(9)所示：

(9)

式中，f为模型的网络函数，Xi为不同的维度，M×N正向导数矩阵的一个元素(i,j)∈[1,…,M]×[1,…,N]是根据一个输入导数Xi的输出神经元Fj，利用式(10)递归地区分隐藏层：

(10)

式中，Hk(X)是隐藏层的输出向量，fk,p是第k层中第j个神经元的激励函数；之后对每一个前向导数和输出标签进行显著性映射，得到的结果作为对抗样本调整的依据：

S(X,t)[i]=

(11)

式中，i是输入特征.最后选取使得所有的显著值中最大的输入特征来调整样本，与原来的值相减以后得到扰动值，以增加分类为特定目标类别的概率，重复这一过程，直到此类别概率大于其他类别或者达到了设定的最大次数停止[15].

(4)C &W法

Carlini等[16]对L-BFGS、FGSM和JSMA等三种方法作出总结改进，用式(12)表示优化问题：

minD(X,X+δ)

s.t.C(X+δ)=Y,X+δ∈[0,1]n

(12)

式中，D是距离约束，如L0、L2和L∞.由于C(X+δ)=Y是高度非线性的，所以上式转化为式(13)，同时可根据不同范数的距离约束进行相应的转化：

(13)

(5)Adversarial Patch法[17]

此方法通过mask来调整 patch的大小和形状，随机让 patch 在图像上进行平移、缩放和旋转，同时使用梯度下降的方法进行优化[15,17].定义一个patch选择器A(p,X,l,t)，p为相应的patch，l为 patch 的位置，X为图像，t为转换操作，先使用选出的p转换相应的对抗结果，再将此结果应用于相应的位置上，在 patch 训练时的优化函数如式(14)所示：

(14)

(6)DDN法

由于C&W攻击通常需要数千次迭代，速度较慢，Rony等[18]提出了解耦对抗性扰动方向和范数的方法.在每一次迭代中，定义一个可以改变范数的影响因子γ，若此时的图像XN不是对抗图像，则使用一个更大的范数lN+1=(1+γ)lN，反之则使用lN+1=(1-γ)lN，此时范数将在决策边界的两侧之间振荡，进而搜索到最佳范数值.最后，将XN+1投影到输入空间的可行区域上.

2.1.2 黑盒攻击

(1)动量迭代梯度法(MI-FGSM)

Dong等[19]将动量的思想运用到基于特定目标类别的黑盒攻击方法中，提高了随机梯度下降中稳定更新的有效性，式(15)为具体更新公式：

(15)

式中，gN收集了前t次迭代的梯度，μ为衰减因子，取为1，α被设定为ε/T.L∞和L2的扩展公式如式(16)所示：

(16)

(2)Curls & Whey法

为了克服黑盒攻击中迭代轨迹难以跨越目标模型的决策边界和对抗样本中的冗余噪声，Shi 等[20]提出了卷曲迭代(Curls iteration)和滤除优化(Whey optimization)相结合的算法.Curls iteration沿替代模型的损失函数的上升和下降方向设置双向迭代，如式(17)所示：

(17)

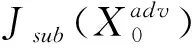
(18)

并在计算每一轮的梯度时在第一步中添加此向量：

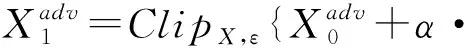
(19)

每一轮之后，在原始图像X和对抗性示例Xadv之间执行二进制搜索：

L=X,R=Xadv,

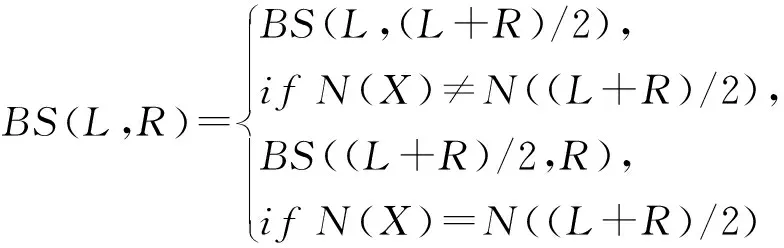
(20)

Curls iteration对原始图像进行梯度下降，如果目标模型上的交叉熵值低于上一步，则开始并进行梯度上升直到最后一步，同时在梯度计算过程中向图像添加了高斯噪声，以提高可传递性.

Whey optimization通过对抗性噪声分组、逐组减小噪声幅度来维持噪声压缩幅度和压缩次数的平衡：

(21)

式中，L(V,N)表示像素值集合V中具有第N个最大绝对值的数字，W、H、C分别表示原始图像X的宽度、高度和通道.最后进一步挤压，σ为每个像素的概率设定值，mask和δ形状大小相同：

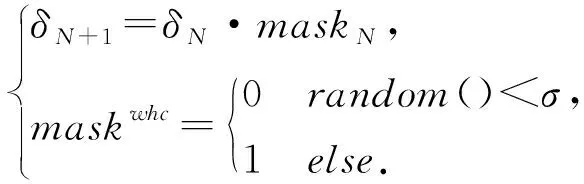
(22)

为了实现特定目标类别的黑盒攻击，将插值集成到迭代过程中：

(23)

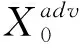
2.2 无特定目标攻击

2.2.1 白盒攻击

(1)迭代梯度法(I-FGSM)

为了提高“快速”性能，Kurakin 等[12]在FGSM生成对抗样本的过程中，加入迭代，改变其原有一步生成的方式，以较小的迭代步长α将其多次应用，并在每一步之后裁剪中间结果的像素值，以确保它们位于原始图像的ε附近，得到对抗性更好的对抗样本，如式(24)所示：

(24)

式中，迭代步长α=1，迭代次数T=min{ε+4,1.25ε}.Clip代表像素裁剪函数，即对图像Xadv进行逐像素裁剪，保证结果将在原始图像X的L∞的ε附近，精确的裁剪公式为式(25)：

Clipx,ε{Xadv}=min{255,X(x,y,z)+ε,

max{0,X(x,y,z)-ε,Xadv(x,y,z)}}

(25)

式中，X(x,y,z)是图像X的通道z在坐标(x,y)处的值.

(2)Vr-FGSM法

Wu等[21]利用减少方差的梯度来生成对抗样本，适用于任何优化器，文中采用了效率更高的Frank-Wolfe优化器且以I-FGSM为例，式(26)为相应的优化公式：

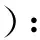
(26)

同时该方法可以解释为生成对高斯扰动有鲁棒性的对抗性示例，再迭代求解：

(27)

式中，Gt为Eξ～N(0,σ2I)[J(X+ξ)]的小批量近似.与IGSM相比，该梯度由平均梯度代替，消除了局部波动，同时增强了可转移性.

(3)分布式攻击法

Zheng等[22]通过尝试寻找最佳对抗数据分布μ*来生成最佳的对抗样本，如式(28)所示，在概率测度的空间上，损失函数由能量函数E(μ)(假设在p(X;θ)达到最小值)来描述，用式(29)表示：

(28)

(29)

式中，KL(μ‖p)是对抗数据分布μ与最佳数据分布p之间的KL散度，c是平衡这两项的超参数.之后提出基于拉格朗日斑点法和离散梯度流法粒子近似方法的两种粒子优化公式(当c=1或M=1时，等效为PGD)，如式(30)和式(31)所示：

(30)

(31)

(4)深度欺骗攻击(Deepfool)

DeepFool通过迭代来生成最小范数对抗扰动，将位于分类边界内的像素一步步修改到边界外，直到出现分类错误为止[23].对于原始像素点X，当添加的扰动垂直于分类器的仿射平面Γ时[15]，此时扰动最小且符合迭代要求：

(32)

在整体迭代过程中，满足以下公式：

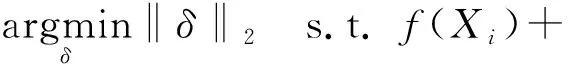
(33)

(5)Universal Adversarial法[24]

深度神经网络存在不可知的固定通用的图像扰动，能够使从原始数据分布μ采样的大多数图像的标签发生变化.为了寻找通用的扰动，在每次迭代中解决式(34)中的优化问题，计算将当前扰动点Xi+v发送到分类器的决策边界的最小范数的额外扰动Δvi来欺骗数据点Xi，并将其汇总到通用扰动的当前实例中[15].

(34)

利用Pp,ε(v+Δvi)进行扰动v的更新，当扰动数据集Xv={X1+v,…Xm+v}超过目标阈值时停止更新：

(35)

(6)Functional Adversarial法

与之前的Lp威胁模型不同，Laidlaw等[25]提出仅允许使用一个函数来干扰输入要素以产生对抗样本，如针对图像颜色的功能性对抗攻击，可以同时将所有红色像素更改为浅红色，与单独的干扰图像的像素相比，图像中的这种全局均匀变化可能会感觉不到.实现功能性特征变换的扰动函数为f:→：

Xadv=f(X)=(f(X1),…,f(Xn))

(36)

通过正则化来保证扰动更不易被察觉，Fdiff可以防止绝对变化超过一定扰动范围，如式(37)，Fsmooth要求在相同的“方向”上干扰相似的特征，如式(38)：

Fdiff{∀Xi∈

(37)

Fsmooth{f|∀Xi,Xj∈⟹

(38)

式中，F为扰动函数f的集合，F选择为Fdiff、Fsmooth、Fdiff∩Fsmooth或完全不同的函数族，之后将威胁模型定义为

tfunc(S){(f(X1),…,f(Xn))|(X1,…Xn)∈

S,f∈F}

(39)

(7)One-step Spectral法[26]

以往的攻击方法都假定输入空间是平坦的，因此,相对于输入的坡度在输出空间中给出了变化最快的方向. 通过使用神经网络中的Fisher信息度量将数据空间视为非线性空间，对于分类任务，网络输出可以视为离散分布的可能性，从而使样本空间成为由非均值测量的流形——线性黎曼度量，可以采用输入的Fisher信息矩阵(FIM)来衡量深度学习模型的脆弱性.最佳对抗性扰动由Fisher信息矩阵的约束二次形式中的第一个特征向量给出，而脆弱性则由特征值反映出来.特征值越大，模型越容易受到相应特征向量的攻击.

将对抗性扰动的优化形式化为FIM的约束二次形式，使用KL散度来测量似然分布的变化.假设深度神经网络的似然分布表示为p(y|X;θ)，由于训练后模型权重θ是固定的，X是攻击时唯一可更改的参数，因此，在条件分布中忽略模型参数θ，并将X作为模型参数.攻击者需要找到一个微小的扰动δ，以使概率p(y|X+δ)从正确的输出变为错误的输出，采用KL散度来测量概率p(y|X)的变化，因此，优化目标可以表述为式(40)：

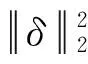
(40)

(8)Strattack法

Strattack通过在图像中滑动面具以提取关键的空间结构来探索对抗性扰动中的群体稀疏性，利用乘数交替方向方法(ADMM)开发了一种有效的优化方法，将原始问题分解为一系列可解析的子问题[27]：

minf(z+X)+γD(δ)+

s.t.z=δ,z=y,z=w

(41)

(42)

式中，h(w)是关于问题约束的指标函数.

2.2.2 黑盒攻击

(1)ONE-PIXEL法

Su等[28]提出基于差分进化(DE)只改变一个像素来生成对抗样本，可以形式化为具有约束的优化问题，用式(43)进行表示：

(43)

一个像素的修改可以视为沿平行于n个维度之一的轴的方向干扰数据点，每次扰动包括坐标x、坐标y和RGB值，对每个像素进行如下迭代操作：

xi(N+1)=xr1(N)+F(xr2(N)+xr3(N)),

r1≠r2≠r3

(44)

式中，xi是候选解决方案的元素，r1、r2、r3是随机数字，F是尺度参数，设定为0.5，N是当前迭代的次数.在每次迭代中，候选解决方案的结果如果优于上一次结果，则进入下一次迭代，如果没有，则上一次结果进入迭代，从而选出最好的单像素扰动样本结果[15,28].

(2)SI-adv法

从安全角度来看，高度稀疏的对抗攻击尤其危险，另一方面，稀疏攻击的像素级扰动通常较大，极易被检测到，所以Croce等[29]提出了一种新的黑盒攻击，旨在最大程度地减少对抗图像与原始图像之间的L0距离.首先检查针对像素的攻击，然后根据分类器输出中产生的间隙对它们进行排序，在排序后的列表上引入概率分布并采样每个像素的变化以产生攻击，这样只允许像素在高度变化的区域内发生变化，并避免沿轴对齐的边缘发生变化，使得生成的扰动几乎不可察觉.

(3)P-RGF法

以往的黑盒攻击方法一般通过使用替代模型的传递梯度或基于查询反馈来近似梯度，但是存在攻击成功率低或查询效率差的问题，Cheng等[30]提出在梯度估计框架下进行查询有效的黑盒攻击方法，成功解决此问题.首先通过向目标模型查询偏向传输梯度的随机向量，进行随机样本的抽取，以充分利用先验信息，然后计算获取梯度损失值，以提供梯度估计，最后在此框架下生成对抗样本.

3 部分生成方法的实验结果对比

本文将第2章中介绍的几种方法进行了实验测试，其中对I-FGSM和MI-FGSM的原理公式进行微小的调整，改动后，I-FGSM的原理公式如式(45)所示，MI-FGSM的原理公式如式(46)所示，迭代步长取为1，迭代次数取为3.

(45)

(46)

实验利用MNIST数据集中的60 000个训练样本和10 000个测试样本对分类器LeNet-5卷积神经网络进行训练和测试，以期提高分类器的准确率，epoch值设为14，经过14次epoch训练和测试后，分类器准确率可达99%，如表1所示，达到实验要求.

表1 分类器训练结果Table 1 Training results of classifier

三种方法的准确率对比如表2所示，对抗性示例如图1所示，从实验结果可见，在相同扰动强度ε下，不同对抗攻击方法的准确率各不相同，准确率大小关系为MI-FGSM>FGSM>I-FGSM，三种方法的准确率都随着扰动强度的增大而降低，且下降趋势都是非线性的，其中FGSM和I-FGSM下降较为明显，在epsilon=0.30时，准确率逐渐降至几乎为0；如图1所示，在相同扰动强度ε下，生成的扰动噪声大小关系为I-FGSM>MI-FGSM>FGSM，且向图像添加扰动的形式各不相同，FGSM和I-FGSM是改变图像的部分明暗度使其变得斑驳，从而达到对抗攻击的目的，MI-FGSM则是通过改变图像的整体明暗度来实现攻击，其攻击有效性更强，生成对抗样本的速度更快，生成的扰动更不易被察觉，说明动量能够很大程度地改良标准的梯度下降方法.

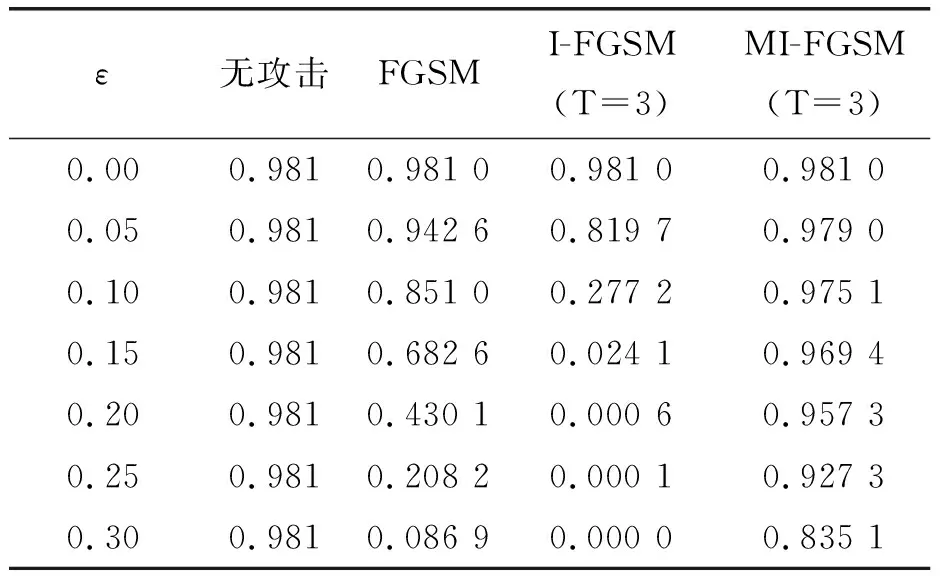
表2 三种方法准确率对比表Table 2 Comparison table of accuracy of three methods

图1 生成的对抗样本Fig.1 Generated adversarial examples

4 对抗样本的应用

对抗样本已被应用于自然语言处理[31]、语音识别[32]、验证码识别[33]、人脸识别[34-35]、道路交通标志检测[36]和医学图像处理[37]等多种场景，本文重点介绍对抗样本在医学领域和道路交通标志检测领域中的应用.

4.1 医疗卫生领域

4.1.1 应用合理性

对抗样本与医疗卫生领域的结合是当前研究的热点，其合理性体现在以下两点：

(1)经济诱因.Finlayson等[37]以美国医疗系统为例，从经济和社会角度进行论证，指出在当前环境下医疗领域中存在有巨大的经济诱因，足以激励潜在的攻击者使用对抗样本对医疗卫生领域的深度学习模型进行攻击.

(2)实际开展.以医学图像处理领域为例，Ma等[38]证明，相较于针对自然图像的深度学习网络，针对医学图像的模型更容易受到对抗样本的影响，即成功进行攻击所需要的扰动更少.其原因可能是医学图像如皮肤镜图像、眼底镜图像等具有非常复杂的生物学纹理，导致模型存在更多的高梯度区，从而使得其对于对抗性扰动更为敏感.此外，在面对对抗样本时，针对医学成像的模型有可能出现较为明显的过拟合，表现出较差的鲁棒性.

综合以上两点，对抗样本在医疗卫生领域的应用有足够的合理性.

4.1.2 应用实例

(1)医学图像领域

2018年，Paschali等[39]首次将对抗样本应用于医学图像中，针对基于Inception模型的皮肤镜图像分类任务和基于U-Net模型的全脑分割任务，分别使用FGSM，DeepFool和SMA方法对其进行了攻击实验，结果表明，即使是已被广泛证明其有效性的医学图像深度学习模型，在对抗性样本的攻击下依然脆弱.

Finlayson等[37]成功使用PGD法和Adversarial Patch法对三个基于ResNet-50的医疗图像分类模型进行了黑盒攻击和白盒攻击.模型分别针对的是视网膜眼底镜检查糖尿病视网膜病变问题(基于Kaggle Diabetic Retinopathy 数据集)、胸部X射线检查气胸问题(基于ChestX-Ray14数据集)和皮肤镜照片检查黑色素瘤问题(基于国际皮肤成像合作网站数据).

Taghanaki等[40]对已有的对抗样本生成方法进行总结，并对胸部X射线图像分类模型进行了全面的攻击实验.同时使用Inception-ResNet-v2和Nasnet-Large模型构建了胸部X射线图像分类网络，制定了判别“疾病”与“非疾病”的二元分类任务，并采用五种基于梯度的攻击方法、两种基于得分的攻击方法和三种基于决策的攻击方法，对两个模型进行了黑盒攻击和白盒攻击.实验结果表明，不同的对抗样本生成方法在医学图像领域有着不同的适用场景，例如,单像素攻击在RGB图像上有着较好的攻击效果，但是在以胸部X光图像为代表的灰度图像上的效果不佳；而基于梯度的攻击方案较之于基于得分和决策的攻击方案，在胸部X光影像分类模型上展示出了更优秀的攻击效果.

此外，另有一些研究验证了各个对抗性样本生成算法对于医学图像模型的攻击有效性，如Ma等[38]在三个基准医学图像数据集上进行了4种攻击方法的实验；Bose等[34]使用对抗样本对基于Inception 和UNet的皮肤病变分类和全脑语义图像分割模型成功进行了攻击等.

(2)医疗文本记录

不同于常规的对医学图像分类或者语义图像分割模型的攻击，Sun等[41]将对抗性的思想引入了电子医疗记录(HER)中，文中使用重症监护医学信息市场(MIMICⅢ)数据，其包含了大型三级护理医院重症监护病房收治的患者有关的信息，建立了由HER数据推测死亡率的模型.针对该预测模型，生成对应的对抗性医疗记录.结果表明，在仅仅更改电子医疗记录不超过3%的情况下，即可成功攻击超过一半的患者.

4.2 道路交通标志检测

4.2.1 应用概述

道路交通标志检测和识别技术在无人驾驶领域处于至关重要的地位，其准确性和稳定性在交通运输安全中起着重要作用，标志不能被成功识别或者标志出现错误分类可能导致灾难性后果，造成不可挽回的损失.因此，将对抗样本生成技术应用于道路交通标志检测和识别系统的攻击中，将对无人驾驶技术产生重大安全威胁.基于以上因素，该问题吸引了越来越多的人进行研究.但是，许多研究也指出，使用该方式进行攻击可能会有许多难点，如①需要综合考虑实际应用场景下的图像亮度、视角、距离和大小调整[36]；②攻击者得到模型参数较为困难，很难进行白盒攻击；③道路标志往往图案简单，相对于自然图片，扰动在人眼看来更加明显，实际情况中能够添加的扰动则会较小，而与之对应的，由于传感器的物理约束，较小的数字扰动可能会使传感器难以检测[42].

4.2.2 应用实例

Eykholt等[43]在2018年提出一种通用的攻击算法——鲁棒物理扰动(RP2)，该算法专门针对道路交通标志检测领域，在不同物理条件下生成相对应的对抗样本.RP2会对图像中的道路交通标志产生干扰，而不会干扰图像中的环境部分.在实验室测试中，不同距离和角度的拍摄的图像达到100%的错误分类，而且对行驶中的汽车中获取的视频帧的84.4%实现成功的攻击，然而，提出的方案并不能完全解决应用概述中提到的难点，无法完全满足人眼不能识别出扰动的要求.

与Eykholt等的思路不同，Sitawarin等[36]从另一个角度解决了道路标志较为简单，扰动看起来更加明显的问题.除了常规的分布内攻击(向交通信号标志图像加入扰动，使其分类错误)外，Sitawarin等提出了分布外攻击方案，将道路上可能存在的商标或旅游区常见的游客标志加入扰动，使其被模型分类为交通信号标志.由于此类图像图案较之于道路标志更为复杂，所以加入扰动后并不十分明显，并且这种方式得到的图像与交通信号标志差别很大，所以可以“隐身”地存在于环境中，利用搭建的真实驾驶测试实验证明了其方案的可行性.

在Sitawarin等[36]工作的基础上，Rgulis等[44]针对速度标志，进行了更加详实的实验.Rgulis等使用德国交通标志图像GTSRB数据集中的速度标志子集，训练生成了对抗样本(针对多尺度卷积网络MSDNet分类器架构)，为保证黑盒情况下的可传递性，使用Dense Net架构的分类器进行测试，实车的实验成功地欺骗了车辆上的TSR系统，首次证明了对抗样本对于商业汽车感知和分类系统也能进行成功的攻击.

除上述攻击方案外，Song等[45]提出了一种新的应用思路，即消失检测攻击.不同于针对分类网络的攻击，该攻击可使得检测器忽略物理对象.Song利用Eykholt 等提出的RP2思想对YOLO v2和Faster-RCNN发起黑盒攻击，有着较好的攻击效果，YOLO在可控的实验室环境中未能识别出86.5%的视频帧，而在室外环境中则无法识别出72.5%的视频帧，对应黑盒攻击这个数字则分别为85.9%和40.2%.与图像分类相比，图像检测需要处理整个场景，并使用对象的方向和位置来确定预测结果，所以通过更改对象的方式进行攻击面临的挑战性更大，如此高比例的成功攻击率，或可以说明检测器模型对于对抗样本的脆弱性.

5 对抗样本面临的挑战和前景预测

5.1 对抗样本的可迁移性

可迁移性是对抗样本的共同属性.Szegedy等首次提出，针对一个神经网络生成的对抗样本可以误导由不同数据集训练的同一神经网络.Papernot等[46]发现，针对一个神经网络生成的对抗样本可以欺骗其他不同框架的神经网络，甚至可以欺骗由不同机器学习算法训练的分类器.在黑盒攻击中，攻击者可以训练一个替代模型，针对替代模型生成对抗样本，由于对抗样本的可迁移性，目标模型也会遭受这些对抗样本的攻击.

对抗样本的可迁移性可归纳为三个方面：①用不同数据集训练的同一结构的模型间的迁移；②为同一任务训练的不同结构的模型间的迁移；③为不同任务训练的模型间的迁移.虽然目前的研究已经涵盖这三个方面，但迁移性攻击的有效性相比于原始模型的攻击仍然大幅度下降，显示出较差的泛化能力.因此，仍需要研究更普遍有效的迁移性对抗样本.

5.2 对抗样本出现的原因

解释对抗样本的出现是一个有趣的话题，对研究人员而言是待解决的根本问题之一，这有助于解释模型的脆弱性和提高抵抗对抗样本的能力.

研究者们已经提出多种假设来解释对抗样本的出现：

(1)数据不完全：对抗样本在测试集中的概率及极端情况的覆盖率都很低[9]，并且对抗样本的分布不同于“干净”样本[47].即便对于一个简单的高斯模型，一个鲁棒模型的建立将会更复杂并需要更多的训练数据[48].

(2)模型能力：神经网络和所有的分类器都会产生对抗样本.对抗样本是模型在高维流型中过于线性的产物[11].Tanay等[49]表明，在线性情况下，当决策边界接近训练数据的流型时，对抗样本就会出现.而不同的是，Fawzi等[50]认为对抗样本的产生是因为分类器对某些分类任务的灵活性过低，线性并非一个很好的解释.Tabacof等[51]将对抗样本的出现归咎为流型的稀疏和不连续性导致模型不稳定.

(3)鲁棒模型不存在：Dong等[52]表明神经网络的决策边界本质上是不正确的，并没有检测到语义对象.如果数据集是由具有较大隐空间的平滑生成模型生成的，则没有针对对抗性样本的鲁棒分类器[53].类似地，Gilmer等[54]证明如果一个模型在一个球面数据集上训练并且错误地分类了数据集的小部分，那么将存在一个带有扰动的对抗样本.

对抗样本为何会出现，至今还是一个开放的问题，相关的讨论仍在持续进行.

5.3 模型的鲁棒性评估

对抗样本的攻击和防御可以看作是一场竞赛：已提出的防御方法能抵御现有的攻击，却对新的攻击方法无效；提出的攻击方法能够击破已存在的防御手段，却被新的方法抵御，如此反复.模型的安全问题日益得到重视，仅仅能抵御现有对抗样本的攻击还远远不够，需要一种更全面的方法来评估模型的鲁棒性，这将有利于了解模型预测的精确性和可依赖性.

当前大多数对抗样本的攻击和防御方法都没有公开的代码，研究人员可能因为实验中的不同设置得出不同的结论，这无疑为模型鲁棒性评估增加难度.此外，对抗样本的应用已拓展到多个领域，广泛的应用也使得模型鲁棒性评估变得困难.因此，能否建立一个通用的标准方法来评估各种情况下模型的鲁棒性也成为亟待解决的问题.

6 结 语

尽管人工智能技术给各个领域提供了强劲的生产动力，但其安全问题也越发引起人们的关注.对抗样本，作为人工智能模型的安全威胁之一，能够诱导模型产生错误预测.近年来涌现出大量相关研究成果，为对抗样本攻防策略的研究提供了重要借鉴.本文梳理和总结了对抗样本的研究成果，并通过实验对部分生成方法进行对比分析，同时将对抗样本在医学领域和道路交通标志检测领域中的应用进行汇总，试图提供一个良好的参考.最后，归纳对抗样本存在的挑战和前景预测，为后续研究提供思路.