基于纵横波保幅分离的粘弹介质弹性波正演模拟*

侯志强, 尹文笋, 李 键, 孙永壮, 刘 云

(中国海洋石油集团有限公司上海分公司，上海 200335)

基于弹性理论的反射波地震勘探技术在能源、资源勘探开发和环境调查等领域发挥了重要作用，但目前随着人们对深部能源勘探开发问题的日益重视和对地球深部地层结构和岩性等问题的持续关注，业界都对深部地层的地震勘探精度提出了更高要求。由于地下岩石普遍具有粘弹性质，常规基于弹性假设的地震勘探技术在解决深部地层的勘探问题时往往表现出不适应性，表现在：(1)对于深部地层，由于地震反射波的传播路径很长，介质粘滞性对地震波传播影响的累积效应增大，地震波的实际传播规律与弹性介质假设情况严重不符，基于弹性介质假设的地震资料处理与反演技术很难取得满意处理效果；(2)岩石粘滞性造成深部地层反射波的高频成分衰减严重，深部地层的地震反射波高频成分缺失，频带变窄，倍频程减小，分辨率降低；(3)岩石粘滞性造成深部地层的反射波能量减弱，信噪比降低，增加了成像难度；(4)地层粘滞性使得不同深度地层反射波的频谱不一致，导致部分处理流程的参数选择困难，同时将成像结果的垂向分辨率变成t0时的函数，导致地下浅、中、深层具有不同的分辨率，增加了解释和反演难度。

研究并利用基于粘弹假设的地震勘探理论和方法可以克服上述缺陷，更好地解决深部地层的精确勘探问题。所谓粘弹介质是指力学性质介于完全弹性和完全粘性之间的介质，这种介质在外力作用下会同时表现出弹性性质和粘性性质，故地震波在这种介质中传播时具有不同于弹性介质的传播机理，这一独特传播机理是研发基于粘弹假设的地震勘探技术的理论基础，因此研究粘弹介质中的地震波传播机理对于解决深部地层的精确勘探问题具有重要意义。

业界对粘弹理论的研究始于1945年的Stokes粘弹地震波动方程[1]，该方程主要考虑了由质点内摩擦引起的地震波能量耗损，之后粘弹地震波传播理论得到了快速发展[2-11]，目前已形成了Kelvin模型、Maxwell介质模型、标准线性介质和达朗贝尔模型等具有不同粘弹性质的连续介质力学模型，其中Kelvin模型是目前地震勘探领域应用最多的粘弹性介质模型。

上述模型对应的地震波方程的解析解或数值解是研究不同类型粘弹介质中地震波传播规律的重要基础，复杂模型条件下地震波方程解析解的求取极为困难，故业界往往采用波动方程的数值解来研究波传播机理或解决实际问题，粘弹介质中地震波方程的数值求解是粘弹地震理论与方法的重要研究内容。

目前，业界用于求取地震波方程数值解的算法主要包括反射率法[3-4]、有限元法[10]、虚谱法[6]、有限差分法[5,8-9,11]等，其中有限差分法由于具有计算速度快、精度高、易实现等优点而得到了广泛应用。本文内容属粘弹性波方程的有限差分数值求解范畴，首先基于交错网格技术[12-13]给出了基于Kelvin模型中的粘弹性波方程的高阶有限差分格式、稳定性条件和吸收边界条件。其次针对粘弹介质中纵横波的解耦问题，本文借鉴完全弹性介质中纵横波的解耦技术[14]，从散度算子和旋度算子出发，通过理论分析给出了一种粘弹介质中纵横波的保幅分离算法，将粘弹介质中的矢量弹性波场分解为矢量纵波场和矢量横波场，再依据纵横波传播方向与偏振方向之间的关系，将三维矢量纵波与矢量横波合成为标量纵波与标量横波，以获取具有实际意义的纵、横波波场和单炮记录，实现了基于纵横波保幅分离的粘滞介质弹性波正演模拟。

1 粘弹介质中的弹性波方程及有限差分求解方法

1.1 三维粘弹介质中的弹性波方程

三维Kelvin模型中的粘弹性波方程为：

(1)

其中：x,y,z为三个直角坐标；t为时间；ρ为密度；vx、vy、vz分别为x,y,z三个方向的质点震动速度分量；σxx,σyyσzz,σxy,σxz,σyz为应力分量；cp为纵波速度；cs为横波速度；Qp为纵波品质因子；Qs为横波品质因子；ω为圆频率。

1.2 三维粘弹介质中的弹性波方程的交错网格有限差分解法

交错网格法[12-13]是指在常规网格中引入半网格点，在半网格点上进行空间导数的计算，把应力分量和速度分量定义在两套网格上。与常规网格相比，交错网格能够有效解决一阶弹性波方程速度分量和应力分量的耦合关系，在不增加计算量的前提下提高计算精度和稳定性。以式(1)中的σxx分量和vx分量为例，它在交错网格空间中的高阶有限差分格式如式(2)、(3)所示：其他分量的差分格式可用类似方法导出。

(2)

(3)

(4)

差分计算方法为：

(5)

式(2)、(3)、(5)的稳定性条件为：

(6)

其中cmax为模型中最大纵波速度。

1.3 吸收边界条件

采用PML边界条件[15-16]解决式(1)求解过程中的截断边界问题。PML吸收边界的基本思想是在计算区域增加吸收层，在吸收层内设置衰减因子对波场进行衰减。对计算区域镶边后的三维空间如图1所示。以vx分量为例，依据PML的分裂思路[15-16]，可将其分解为x,y,z三个方向的分量vx_x，vx_y，vx_z，即：

vx=vx_x+vx_y+vx_z。

(7)

各分量的吸收方程如下：

(8)

其中d(x)、d(y)、d(z)分别为x、y、z三个方向上的衰减因子，其取值详见文献[15]。

在不同的边界对不同的分量进行吸收即可压制截断边界的伪反射。仍以vx分量为例，在图1所示的三维吸收边界示意图中，各个边界区域的衰减因子如下：

图1 三维空间PML吸收边界示意图

2 纵横波保幅解耦方法与矢量纵横波的标量合成

2.1 纵横波保幅解耦方法

式(1)中vx、vy、vz的本质是质点的振动速度矢量v在直角坐标系三个坐标轴上的投影，由于纵波与横波均可引起这三个方向上的质点振动，因此vx、vy、vz分量都同时包含纵波与横波，两种波耦合在一起不便于分析纵横波的传播与衰减机理，因此有必要在粘弹介质弹性波方程正演的过程中采用适当方法对纵横波进行解耦，以得到合成纵波记录和横波记录。

各向同性介质中纵波是无旋场，横波是无散场，因此可通过求取弹性波场的散度与旋度得到纵波场与横波场，Aki和Richards以此为基础，利用v的散度和旋度算子实现了弹性介质中的纵横波分离[17]，这种方法实现简单，计算量小，但会使波场的相位和振幅信息产生畸变[18-19]，且分离后的波场在极性反转位置上无法与分离前混合波场各分量对应，因此基于散度和旋度算子的波场解耦方法是不保幅的。

由于本文研究的Kelvin模型仍属于各向同性介质范畴，因此弹性各向同性介质中基于散度与旋度算子的波场解耦方法同样无法解决Kelvin模型的纵横波保幅分离问题。本文的主要目标就是研究新的方法实现Kelvin粘弹模型的纵横波保幅分离。

假设Kelvin粘弹模型中的矢量波场v由vp和vs两个矢量场组成：

v=vp+vs。

(9)

其中vp为由纵波引起的质点振动速度矢量；vs为由横波引起的振动速度矢量，这两个矢量在笛卡尔坐标系中的表达形式为vp=(vp_x,vp_y,vp_z)，vs=(vs_x,vs_y,vs_z)。

对式(9)分别求散度和旋度可得：

(10)

由于纵波为无旋场，横波为无散场，有：

(11)

(7)式可写为：

(12)

将上式变换到波数域，有：

(13)

纵横波的波数域单位传播矢量Kp、Ks与纵横波速度及圆频率ω之间满足以下关系：

(14)

联立式(10)和式(11)可得：

(15)

对上式作傅里叶反变换，可得

(16)

上式即为各向同性粘弹介质中的纵横波保幅分离算子，它可以在时间空间域利用有限差分来实现，具体计算公式为：

(17)

和Aki等的方法[17]相比，本文方法的优势在于：不会引起纵横波振幅和相位畸变，且将纵波当作矢量进行处理，在物理意义和波场的极性反转位置上能与分离前混合波场各分量对应；和李振春等的方法[20]相比，本文方法的优势在于：首先利用地层中纵横波的传播速度对分离后的矢量波场进行振幅补偿，对补偿结果再沿时间方向进行积分使得分离结果更具保真性。

利用图2a所示的水平层状模型验证本文算法的保幅性，两层介质的纵波速度分别为2 500、3 000 m/s，横波速度分别为1 443、1 764 m/s，密度分别为2 000、2 500 kg/m3，纵、横波品质因子为常数80，界面埋深400 m。波场模拟所用的参数为：震源为主频f0=35 Hz的雷克子波，震源置于地表，其水平位置为(500 m，250 m)，空间网格大小5 m×5 m，时间步长0.5 ms。由于本文是在时间域对式(1)进行求解，故假定圆频率ω为常数，其值为2πf0。图2b～2d为正演过程中记录t=350 ms时的三分量波场快照，由图可见，每个分量快照中都同时包含纵波与横波，纵横波耦合在一起，互为串扰，必须将之分解为相对独立的纵波分量和横波分量才便于分析粘弹介质中的纵横波传播规律。

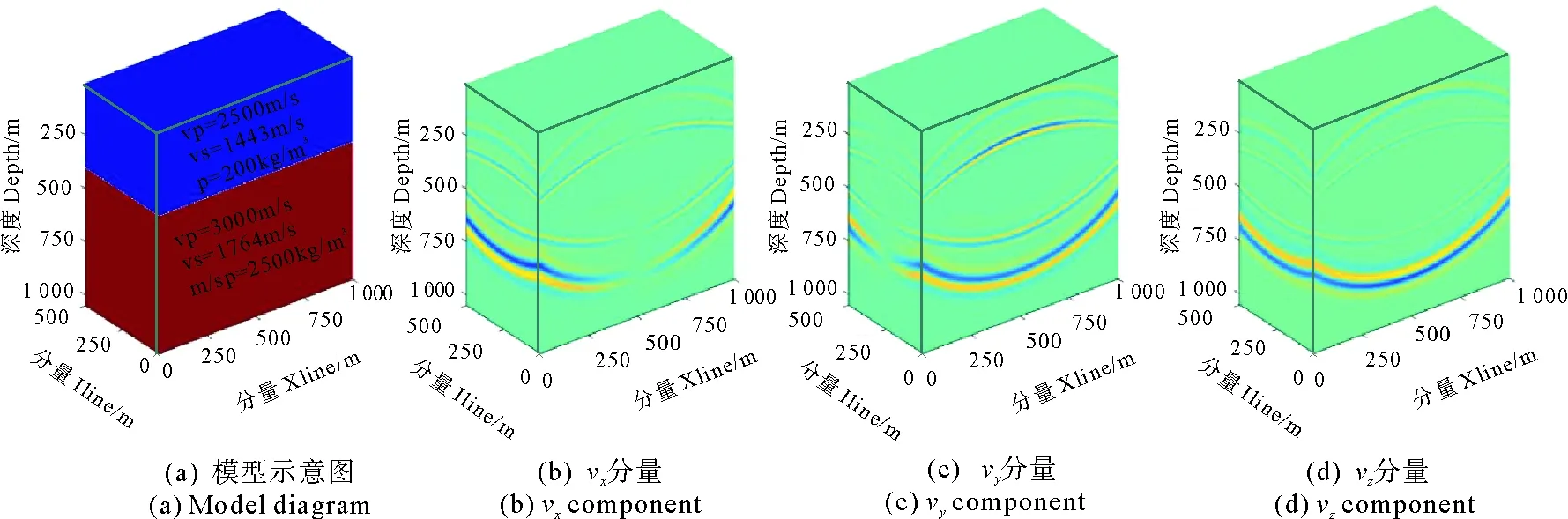
图2 模型示意图及其三分量快照

在正演模拟过程中分别利用Aki等的方法[17]、李振春等的方法[20]和本文算法进行波场解耦。图3、4和5分别为上述三种方法的纵横波解耦结果快照，由图可见，这三种方法都能在波场模拟过程中实现纵横波的解耦，其中Aki的方法[17]将弹性波场分解为标量纵波和矢量横波，后两种方法则将弹性波场分解为矢量纵波和矢量横波，由于标量可以看作一种特殊的矢量，因此解耦结果中的纵波无论是标量还是矢量，在理论上都是正确的。但图3中矢量横波各个分量中的极性反转位置与原波场不一致，同时分离结果中横波的z分量(见图3d)在inline方向的波场值为零，这与vz分量中的横波存在明显差异，这些现象说明散度算子和旋度算子对横波场具有改造作用，它无法得到地下真实的横波场，只能得到改造后的横波场。

图4、图5为采用后两种方法得到的纵横波分离快照，由图可见，这两种方法都能实现纵横波的完全解耦，且解耦前后纵、横波各分量的极性反转位置能够准确对应，这表明后两种方法的解耦精度高于散度和旋度算子。但对于纵波的三个分量，李振春等的方法[20]得到的结果与分离前的数据存在90°的相位差，而本文方法与原始数据之间不存在相位变化，说明本文算法的解耦精度高于第二种方法。

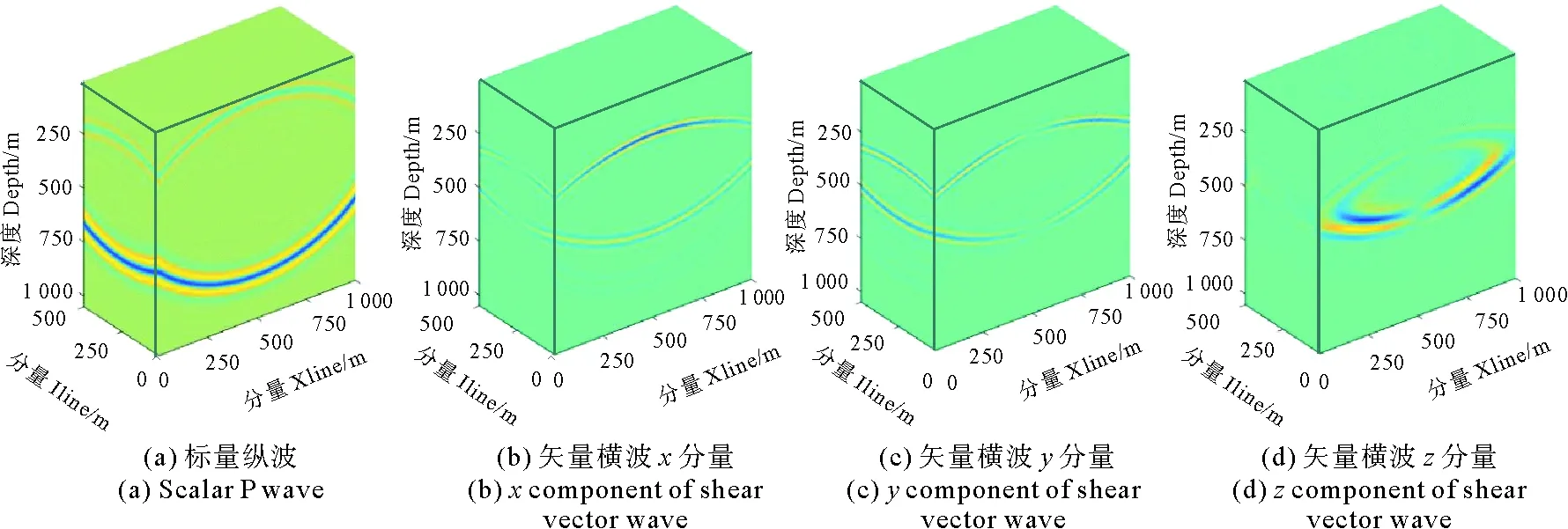
图3 散度和旋度算子的波场解耦快照

图4 李振春等算法的波场解耦快照

图5 本文算法的波场解耦快照

为证明本文算法的保幅优势，从不同方法分离前后的快照结果中选取一道数据进行比较，该道在地表的投影位置为：(650，50)，图6a为不同方法分离前后的纵波z分量显示，其中第一道数据为波场分离前的z分量混合波场，第二道为利用散度算子[17]得到的标量纵波，第三、第四道为分别利用李振春等[20]和本文算法得到的矢量纵波z分量，由图可见，本文算法得到的纵波z分量结果与原波场中的纵波的振幅和相位完全一致，而另外两种方法得到的结果的振幅比原波场小1～2个数量级，且存在90°相位差。图6b为不同方法分离前后的横波x分量显示，其中第一道数据为场分离前的x分量混合波场，其余三道分别为利用旋度算子、李振春等的方法和本文算法得到的矢量横波的x分量，三种方法对横波的分量结果都不存在相位畸变，但前两种分离算法分离结果的振幅比原始数据小一个数量级，本文方法的分离结果则与分离前的横波完全一致。图7为该位置处用不同方法得到的正演单道记录的比较，分析该图可以得到与图6相同的结论，这表明本文给出的粘弹介质纵横波分离方法是保幅的。

2.2 矢量纵、横波的标量合成方法

本文的纵横波保幅解耦方法能为研究粘弹介质纵、横波的传播规律提供保真的数据，还能为基于点积互相关的弹性波逆时偏移成像[21]提供保真的矢量纵波和矢量横波数据。但在常规逆时偏移技术[22-23]中往往需要用标量的纵波与横波进行互相关成像，同时，工业界也倾向于利用更具明确地球物理意义的标量纵波与标量横波来解决地质问题，在这种情况下就需要对分离后的矢量纵波与矢量横波进行标量合成。

矢量波场的标量合成问题一般由振幅计算和极性确定两部分组成。对于标量波的振幅计算问题，不管是纵波还是横波，都可以通过求取矢量波场的模来完成，问题的难点在于如何确定标量化后的波场的极性。本文采用质点振动法求取标量横波的极性[24]，对于标量纵波的极性问题，本文规定质点振动方向与z轴夹角小于90°时为负，反之为正，由此可以将纵波的极性求取问题转换为质点振动方向的求取问题，由于纵波的传播方向与质点的振动方向相同，因此可利用纵波的传播方向确定质点振动方向，进而确定标量纵波的极性。纵波的传播方向信息可利用坡印廷矢量得到，弹性波坡印廷矢量的求取方法已有多人做过研究[25-26]，本文不赘述。图8为利用上述原理对图5所示的波场快照进行标量合成的结果，标量合成后的纵、横波场具有更为明确的物理意义且更便于实际应用。

图6 不同分离方法得到的波场快照比较

图7 不同分离方法得到的合成记录单道比较

图8 矢量纵、横波标量化后的快照

3 模型算例

模型的纵横波速度如图9所示，纵、横波品质因子均取常数80，正演所用的参数如下：模型大小为1 500 m×250 m×1 050 m，空间网格大小为5 m×5 m×5 m，采用间隔为0.35 ms，记录长度为1.05 s。采用Ricker子波作为震源，主频为35 Hz，震源位于(760 m，250 m,0 m)处，三线接收，线距50 m，每条测线300道接收。图10为基于本文算法的合成纵波记录和转换横波单炮记录，图11为该模型完全弹性情况下的合成反射纵波记录和转换横波记录，对比图10，11可以看出粘弹介质情况下，由于受到地层的粘滞吸收作用，反射纵波和转换横波的能量均弱于弹性情况，图12为第1条线100道纵、横波分量中的375～900 ms时间段波场对比图，图中无论是纵波还是转换横波，介质完全弹性情况下的振幅明显高于粘弹情况，且随着时间的增大，这种差别也逐渐增大，其原因为：传播时间的增大往往意味着传播距离的增加，即传播的波长数增大，介质粘滞性的累积效果增加。

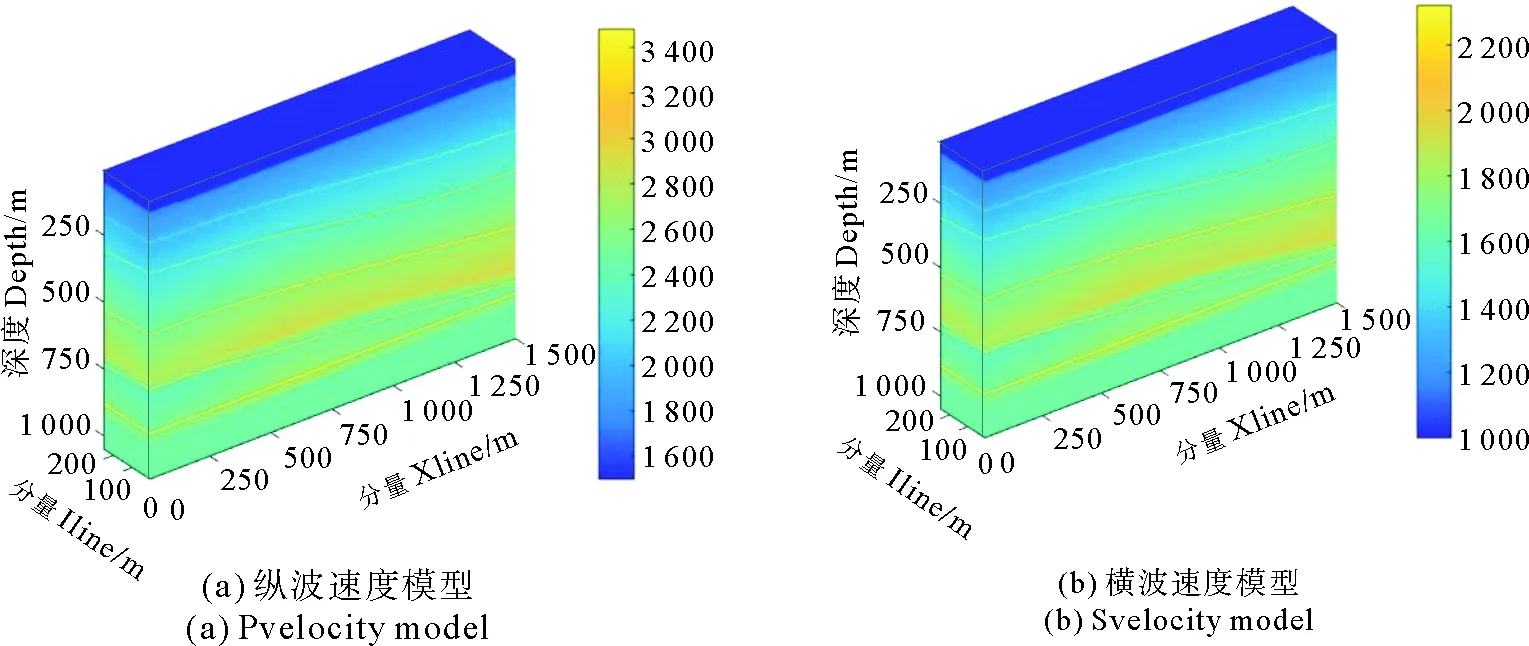
图9 纵横波速度模型

图10 粘弹条件下的合成纵横波记录

图11 完全弹性条件下的合成纵横波记录

图12 不同条件下第1条线100道地震记录对比

4 结论

(1) 本文将标量纵波看作一种特殊的矢量，推导了三维粘滞弹性波的纵横波保幅解耦公式，给出了差分求解方法。本文算法的解耦结果能够实现与原三分量波场的对应，解耦结果可方便的用于波场分析，且具有很高的保幅性。

(2) 本文算法解耦后的纵、横波三分量数据可直接用于基于点积互相关的逆时偏移成像；纵、横波的标量合成结果可直接用于常规的弹性波逆时偏移成像。

(3) 本文基于纵横波保幅分离的粘弹介质弹性波正演模拟算法既可以获得常规三分量合成地震记录，也可以获得波场解耦后的纵波合成记录与转换横波合成记录，还可以获得三分量矢量纵波记录和矢量横波记录。