链路统计分析中导出参数概率计算方法研究
李赞,樊敏
北京跟踪与通信技术研究所,北京 100094
随着中国对月球和深空探测的不断深入,测控距离显著提高,信号衰减急剧增大,通信链路变得越发紧张,同时对链路性能的可靠性和数据量要求也越来越高。如何充分发挥现有测控设备能力,合理确定天地链路参数、准确预报和确定天地链路性能,对提高系统可靠性、最大限度获取各类探测数据、有效节省系统资源和项目经费都具有重要意义。
在中国以往航天任务的测控链路设计中,为了确保上下行测控的绝对可靠,链路预算通常较为保守,即链路参数的取值均采用最恶劣的情况计算。在实际任务中,各参数并非同时在最恶劣的状态下工作,同时各链路参数都具有统计特性,服从一定的概率分布。因此,为了适应更远深空探测的任务需求,有必要充分考虑链路参数统计特性和使用场景,在确保满足使用需求的情况下,对链路性能进行合理、有效评估。
20世纪70年代,Yuen建立了统计链路分析框架,用于美国喷气推进实验室深空任务的链路分析和设计[1-3]。通过各链路参数服从的概率密度函数、以及其设计值、有利容差(最优值与设计值的差)和不利容差(最差值与设计值的差),计算得到具有一定置信度的链路余量。
此后,美国喷气推进实验室及其深空网在各航天任务中持续对链路参数进行测量和分析,研究其统计特性,并将统计数据用于链路性能的预测和评估,逐步提高链路预测精度[3]。随着测量值的不断丰富和链路参数服从概率密度函数的逐步完善,CCSDS在其蓝皮书中,明确给出了航天任务链路预算过程,同时给出了各链路参数服从的概率密度函数和链路性能计算方法[4-5]。

当链路参数不满足Lyapunov条件时,导出参数就无法利用高斯型概率密度函数进行计算,从而无法完成链路性能的统计分析。另外,Babuscia等给出的导出参数的概率密度函数均为高斯型[6],但CCSDS 401.0-B-29给出的导出参数的概率密度函数与Babuscia给出的不完全相同,如:CCSDS 401.0-B-29给出的有效全向辐射功率(effecitve isotropic radiated power,EIRP)、上行接收载波功率、上行接收数据余量等导出参数服从三角分布,但下行接收数据余量、测距余量等服从高斯分布[4]。
针对上述问题,本文首先研究了统计链路分析的理论方法,分析了CCSDS建议中各链路参数采用不同概率密度函数的主要原因,进而给出了链路参数不满足Lyapunov条件时进行统计分析的基本方法,最后举例说明并比较了两种不同情况下导出参数的计算过程。
1 统计链路计算的理论分析
链路性能分析使用的基本公式[5]如下:
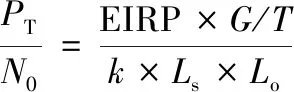
(1)
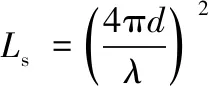
将式(1)以分贝形式表示,如下:

(2)
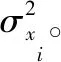
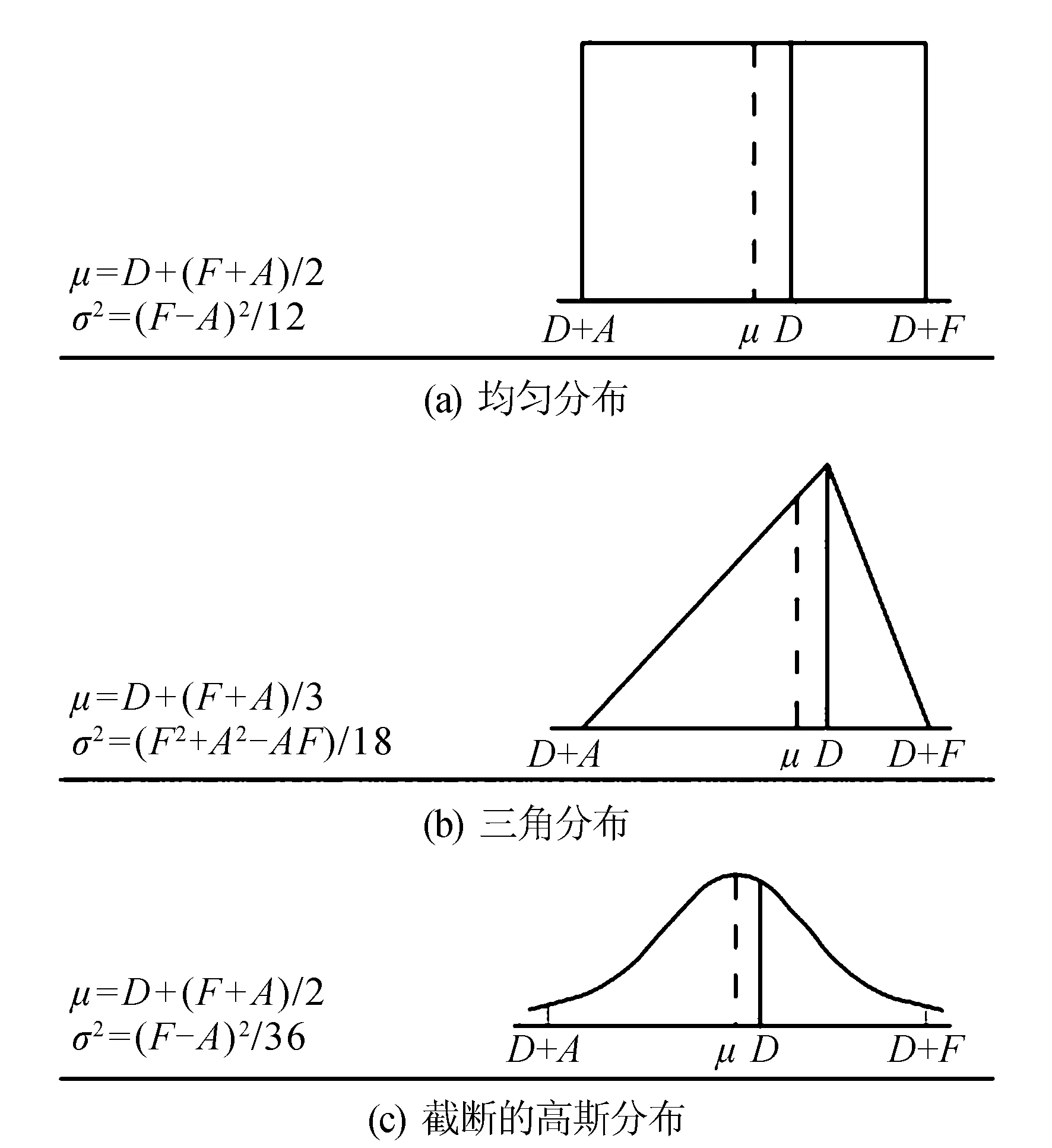
图1 常用链路参数的概率密度函数及相关特征参数Fig.1 Probability density functions of common link parameters and related characteristic parameters

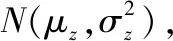

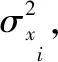

(3)

Lyapunov条件的物理意义是:独立随机变量序列xi(i=1,…,n)中的每个随机变量均具有有限均值和方差,且不存在xi,其方差远大于其他xj的方差。因此,若链路计算中与导出参数相关的各参数满足Lyapunov条件,则导出参数近似服从高斯分布。
当参与计算导出参数的各链路参数的设计值、有利容差、不利容差已知,且满足Lyapunov条件时,近似认为导出参数服从高斯分布,直接对相关链路参数的均值、方差求和得到导出参数的均值和方差。
当某一链路参数的方差远大于其他参数的方差,即不满足Lyapunov条件时,采用文中给出的通过计算尾概率的方法计算导出参数取值的概率,进而得到导出参数取值的概率。
2 统计链路特性分析
2.1 标准建议的3种概率密度函数特性分析


(4)
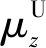
分析式(4)可知,在通常情况下(有利容差和不利容差相差不大时),链路参数的概率密度函数为三角型时方差最大,为高斯型时方差最小。利用统计法分析链路性能时,若将概率密度函数取为三角型,统计分析结果比高斯型保守或者说可靠性高。CCSDS 401.0-B-29建议上行链路导出参数的概率密度函数多采用三角型,下行链路余量多采用高斯型,也正是从上行链路的可靠性要高于下行链路考虑得到的[4]。
2.2 满足Lyapunov条件导出参数的概率密度函数
实际链路计算过程中,可以通过以下两种方法计算导出参数的均值和方差:
1)分别将各链路参数的设计值、有利容差、不利容差相加得到导出参数的设计值、有利容差、不利容差,进而通过高斯概率密度函数,计算得到导出参数的均值和方差。
2)分别将各链路参数的均值和方差直接相加得到导出参数的均值和方差。
由上文可知,当各链路参数满足Lyapunov条件时,导出参数近似服从高斯分布,导出参数的均值和方差近似等于各链路参数均值和方差的和。因此,需要采用上述方法2计算得到导出参数的均值和方差,当采用方法1时,将会产生较大偏差,后续将通过实例说明。
2.3 不满足Lyapunov条件时导出参数概率密度分析
利用高斯函数近似作为导出参数的概率密度函数能够大大简化计算过程,但当某些链路参数的方差明显较大,即不满足Lyapunov条件时,就不能使用高斯函数进行近似计算,必须借助其他手段进行分析。
直接通过对各链路参数的概率密度函数求卷积来计算导出参数概率密度函数的过程极其复杂,工程应用中难以实现。本文介绍了一种使用鞍点逼近估计尾函数的方法,近似确定导出参数的概率,进而得到导出参数的方差[9]。以下重点针对该方法的理论计算和实际分析过程进行说明。
定义导出参数概率密度函数fy(y)的特征函数为:

(5)
根据卷积函数特性,导出参数的特征函数为各链路参数特征函数的乘积,但该方法的难点在于通过导出参数的特征函数反解导出参数的概率密度函数。为此,本文利用Helstrom提出的鞍点逼近估计尾函数的方法确定导出参数的概率[6],该方法对概率密度函数极其复杂但非常适用于其特征函数已知时,如对距离均值1倍以上方差(1σ)位置的概率估计,尤其适用于链路性能预算中对2σ或3σ余量的估算。利用该方法,能够根据概率值(1σ为68.3%,2σ为95.5%,3σ为99.7%)直接得到导出参数满足1σ、2σ或3σ的参数值。
尾概率函数q+(α)[7]定义为:

(6)


(7)
对Ψ(s)进行泰勒级数展开,并取二阶项,则尾概率函数q+(α)可近似表示为:
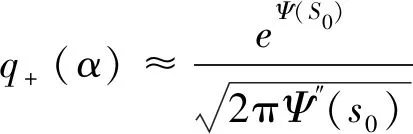
(8)
式中:Ψ″为Ψ(s)的二阶导数。
通过求解上述方程,可以得到不同α值(即导出参数值)对应的尾概率。在实际计算过程中,通常根据各链路参数的特征函数计算导出参数的特征函数,根据α的定义域,采用数值方法解式(7),得到不同α值对应的s,进而根据式(8)计算α定义域内的尾概率q+(α),得到导出参数与其概率的关系曲线。
常用概率密度函数的特征函数[8]如表1所示。

表1 常用概率密度函数的特征函数
3 算例分析
通过两个算例描述链路参数满足和不满足Lyapunov条件时,导出参数的概率分步分别利用高斯分布和鞍点逼近估计尾函数的方法进行计算的过程,并与真实导出参数的概率密度函数进行比较,验证上文理论分析的正确性。
3.1 满足Lyapunov条件
假设4个链路参数为独立的随机变量xi(i=1,2,3,4),其中x1和x2服从均匀分布,x3服从三角分布,x4服从高斯分布,各链路参数的概率密度函数和相关特征参数如表2所示。

表2 算例1链路参数的概率密度函数及相关特征参数
导出参数的概率密度函数fz(z)是通过对表2中各参数概率密度函数求卷积得到,进而计算得到导出参数z均值和方差的真值,分别为:

通过表2可以看出,各链路参数不存在某一参数的方差远大于其他参数,满足Lyapunov条件,导出参数近似服从高斯分布,其均值和方差可通过对各链路参数的均值和方差求和得到,即:
高斯分布的概率密度函数为:
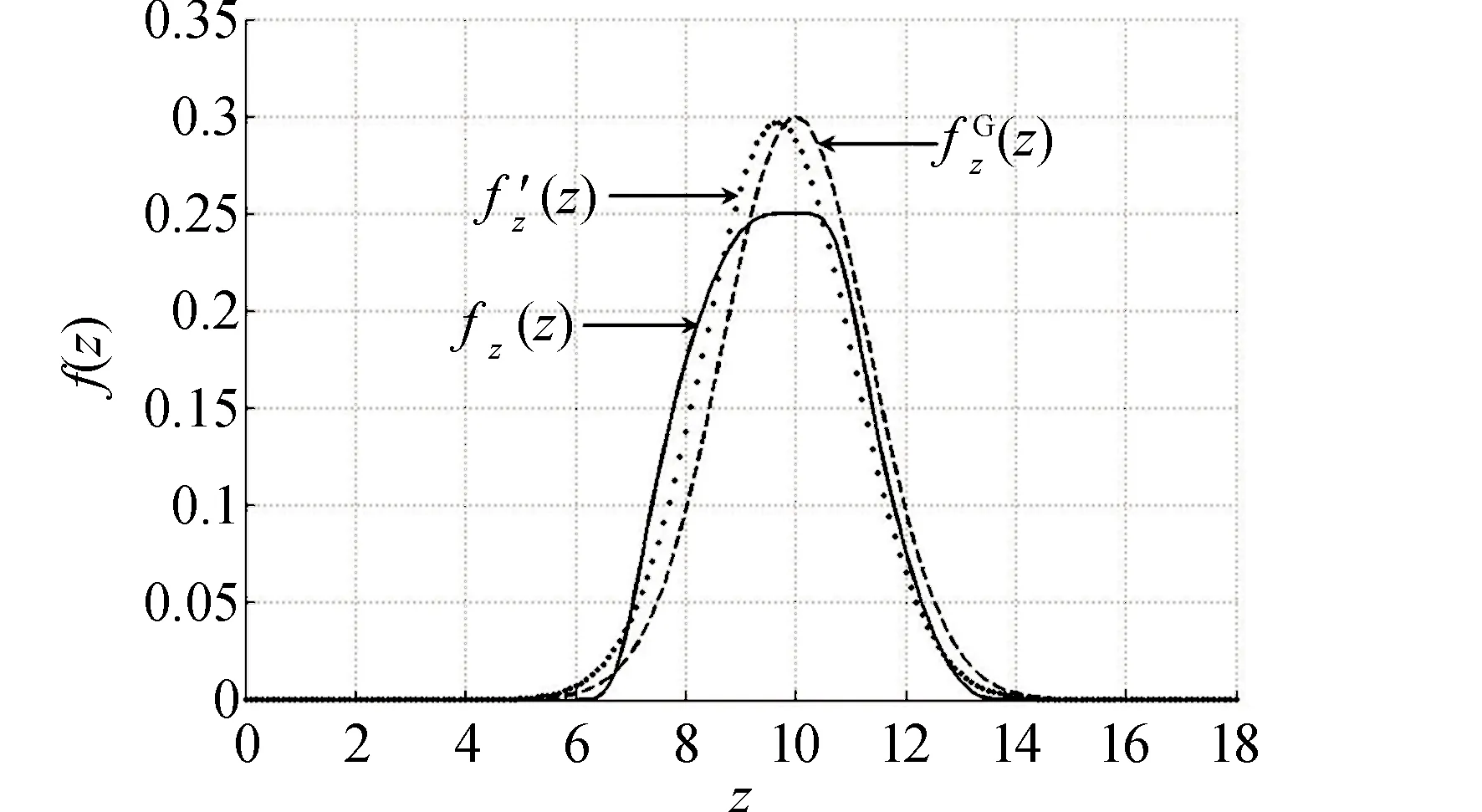
-∞ 当导出参数的均值和方差利用其设计值、最大值、最小值及服从的概率密度函数计算得到时,可得: 其概率密度函数为: -∞ 图2 算例1近似高斯和精确概率密度函数比较Fig.2 Comparison between Gaussian approximate probability density function and accurate probability density functions of example 1 根据表3,假设导出参数符合高斯分布,且其均值和方差为各链路参数均值和方差的和,可得导出参数的均值和方差为: 其概率密度函数为: -∞ 当利用导出参数的设计值、最大值和最小值计算得到其方差时,可以得到以下结果: 相应的概率密度函数为: -∞ 用鞍点逼近计算尾概率密度函数的方法计算这种情况下的概率。 表3 算例2参数的概率密度函数及相关特征参数 图3 算例2近似高斯和准确概率密度函数比较Fig.3 Comparison between Gaussian approximate probability density function and accurate probability density functions in example 2 由表1和表3可得,导出参数概率密度函数的特征函数为: (e7s-6e9/2s+5e4s) 由此可以得到函数Ψ(s)为: 求解Ψ(s)的一阶导数Ψ′(s)和二阶导数Ψ″(s)。 根据各链路参数的定义域可得导出参数α的定义域为[6,14],在此定义域内,利用式(7)和式(8)计算得到α取不同数值时对应的Ψ(s0)和Ψ″(s0),由此可以求出相应的尾概率q+(α),其中q+(α)=0.317、0.045、0.003分别对应α值为偏离1倍、2倍和3倍方差的导出参数值。 图4给出了导出参数的尾概率密度函数q+(α)与准确概率函数q(α)的关系。表4分别给出了偏离1σ、2σ和3σ时对应的α值。由图4可知,采用鞍点逼近计算尾函数的方法可以很好地估计导出参数的概率分布,尤其在偏离2σ和3σ时,基本与准确概率相同。 图4算例2导出参数尾概率与准确概率对比曲线Fig.4 Comparison curves between tail probability and exact probability of derived parameters in example 2 表4 实例2导出参数的概率值 从以上例子可以得出:当链路参数不满足Lyapunov条件时,不能用高斯概率密度函数近似对导出参数进行统计分析;而用尾概率的方法能够对距离均值1倍以上方差(1σ)位置的概率进行较好的估计,1倍以下方差难以真实反映导出参数的概率统计特性;用尾概率函数能够直接得到满足1倍(1σ)、2倍(2σ)和3倍(3σ)标准方差的导出参数值,进而可直接用于链路估算。 在实际链路计算过程中,应首先确定链路参数是否满足Lyapunov条件,若不满足,则导出参数可利用计算尾概率密度函数的方法计算导出参数的均值和方差,但导出参数的设计值、最小值和最大值仍利用各链路参数的设计值、最小值和最大值求和得到。 通过本文的理论推导和分析,可以得到以下结论: 1)利用统计法分析链路性能时,若将概率密度函数取为三角型,统计分析结果比高斯型要保守或者说可靠性要高; 2)当与导出参数相关的链路参数满足Lyapunov条件时,导出参数的概率密度函数采用高斯分布能够达到很好的近似效果,且大大简化了计算复杂度; 3)当利用高斯函数对导出参数的概率密度函数近似时,导出参数的均值和方差应通过对各链路参数的均值和方差求和得到; 4)当链路参数不满足Lyapunov条件时,利用鞍点逼近估计尾概率密度函数的方法能够较准确地确定导出参数的概率。

3.2 不满足Lyapunov条件

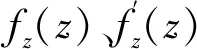



4 结束语

